Ciencia, Ingenierías y Aplicaciones, Vol. 7, No. 2, julio-diciembre, 2024 ISSN (impreso): 2636-218X • ISSN (en línea): 2636-2171
Análisis comparativo del comportamiento sísmico entre una edificación de acero con sistema DIAGRID y una con Arriostramientos Concéntricos en Portoviejo-Ecuador
Comparative analysis of the seismic behavior of a structure with a DIAGRID structural system and a structure with concentric bracing in Portoviejo- Ecuador
DOI: https://doi.org/10.22206/cyap.2024.v7i2.3371
Recibido: 16/11/2024 • Aprobado: 30/12/2024
Cómo citar: Pico Zambrano, G. X., Cagua Gómez, B. J. (2024). Análisis comparativo del comportamiento sísmico entre una edificación de acero con sistema DIAGRID y una con arriostramientos concéntricos en Portoviejo-Ecuador. Ciencia, Ingenierías y Aplicaciones, 7(2), 171-208. https://doi.org/10.22206/cyap.2024.v7i2.3371
Resumen
Este artículo presenta un análisis comparativo del comportamiento sísmico de dos sistemas estructurales aplicados a una edificación de acero de baja altura en Portoviejo, Ecuador: el sistema DIAGRID (PIMD) y los Pórticos Arriostrados Concéntricamente (PEMAC). El objetivo de la investigación es evaluar la eficacia de estos sistemas bajo condiciones sísmicas de diseño, utilizando procedimientos tradicionales establecidos en la normativa nacional, como el análisis modal espectral y el método estático equivalente. Además, se examinan propiedades dinámicas, cortantes basales, derivas laterales, capacidad axial y la eficiencia en el uso de materiales.
Los resultados muestran que el sistema DIAGRID (PIMD) presenta una rigidez lateral significativamente superior, evidenciada por períodos de vibración menores (0.38 s en PIMD frente a 0.63 s en PEMAC) y una reducción del desplazamiento lateral de aproximadamente un 50% en comparación con el sistema PEMAC. Esta configuración permite una distribución más eficiente de las fuerzas laterales, reduciendo las deformaciones y mejorando el desempeño sísmico general. Además, el sistema PIMD logró una disminución del 3.64% en el consumo de acero, lo que se traduce en un ahorro significativo en los costos de construcción sin comprometer la seguridad estructural.
El sistema DIAGRID (PIMD) se presenta como una alternativa robusta y eficiente para edificaciones de acero en regiones de alta sismicidad, ofreciendo ventajas en rigidez, economía de materiales y desempeño sísmico. Estos hallazgos proporcionan una base sólida para guiar a ingenieros y diseñadores en la adopción de tecnologías estructurales avanzadas, contribuyendo a la resiliencia de infraestructuras en contextos sísmicos.
Palabras clave: Sistema DIAGRID; pórticos arriostrados; comportamiento sísmico; Estructuras de Acero; Portoviejo.
Abstract
This article presents a comparative analysis of the seismic behavior of two structural systems applied to a low-rise steel building in Portoviejo, Ecuador: the DIAGRID system (PIMD) and Concentrically Braced Frames (PEMAC). The objective of the research is to evaluate the efficacy of these systems under design-level seismic conditions utilizing conventional procedures established in the national code, such as the modal spectral analysis and the equivalent static method. Furthermore, dynamic properties, base shear forces, lateral drifts, axial capacity, and material efficiency are examined.
The results indicate that the DIAGRID system (PIMD) demonstrates significantly higher lateral stiffness, as evidenced by shorter vibration periods (0.38 s in PIMD versus 0.63 s in PEMAC) and a reduction in lateral displacement of approximately 50% compared to the PEMAC system. This configuration facilitates a more efficient distribution of lateral forces, minimizing deformations and enhancing overall seismic performance. Moreover, the PIMD system achieved a 3.64% reduction in steel consumption, resulting in substantial cost savings without compromising structural integrity.
The DIAGRID system (PIMD) emerges as a robust and efficient alternative for steel buildings in high-seismicity regions, offering advantages in stiffness, material economy, and seismic performance. These findings provide a substantive foundation to guide engineers and designers in the adoption of advanced structural technologies, contributing to the resilience of infrastructure in seismic contexts.
Keywords: DIAGRID system; braced frames; seismic behavior; steel structures; Portoviejo.
1. Introducción
El diseño de estructuras sismorresistentes se ha consolidado como un pilar fundamental en la ingeniería estructural, dada la amenaza que representan los terremotos a nivel global. Entre el año 2000 y 2019, los terremotos causaron aproximadamente 721 mil muertes y pérdidas económicas estimadas en 636 mil millones de dólares a nivel mundial (Chen & Zhang, 2022; The Human Cost of Disasters, 2020), evidenciando la necesidad de enfoques de diseño que garanticen la estabilidad estructural y reduzcan el riesgo de daños. La ingeniería sísmica moderna busca crear estructuras resilientes que, además de soportar movimientos sísmicos severos, mantengan su funcionalidad tras un sismo, facilitando la recuperación de las comunidades afectadas (Tena-Colunga & Hernández-Ramírez, 2020).
En este contexto, aún persisten desafíos significativos, particularmente en edificaciones convencionales de países en desarrollo, como se observó recientemente en India, donde la falta de implementación de principios de diseño sismorresistente resultó en daños severos (Chandra Dutta et al., 2021). Ejemplos adicionales incluyen el terremoto de Haití en 2010, que devastó Puerto Príncipe y dejó a 1.5 millones de personas sin hogar debido a construcciones deficientes (Bilham, 2010), y el terremoto de Nepal en 2015, que afectó gravemente Katmandú, causando la destrucción de edificios históricos y la pérdida de miles de vidas (Goda et al., 2015). Más recientemente, el terremoto de 2023 en Turquía y Siria mostró el devastador impacto de no cumplir con normas sismorresistentes, con miles de edificaciones colapsadas y más de 50,000 muertes (Kinik, 2023; Ozturk et al., 2023). Estos eventos subrayan la necesidad de adoptar códigos de construcción sismorresistentes para proteger a las comunidades de futuros desastres.
En respuesta a estos desafíos, los avances en tecnología estructural y códigos de diseño han facilitado el desarrollo de sistemas innovadores, como el DIAGRID y los pórticos arriostrados concéntricamente (SCBF). Estos sistemas han demostrado su eficacia en la resistencia a cargas sísmicas, debido a configuraciones que optimizan el uso de materiales y mejoran la rigidez global del edificio (Carrillo et al., 2014; Lu et al., 2016; Terán-Gilmore et al., 2021). La estructura DIAGRID, caracterizada por una malla triangular de elementos diagonales, es particularmente efectiva para soportar fuerzas sísmicas y cargas de viento (Terán-Gilmore et al., 2021). En paralelo, los pórticos arriostrados concéntricamente se utilizan ampliamente para distribuir fuerzas laterales y reducir desplazamientos en edificaciones (Bigonah et al., 2024).
La alta sismicidad de Ecuador, ubicada en la convergencia de las placas de Nazca y Sudamericana, representa un desafío constante para el diseño de infraestructuras resilientes (Beauval et al., 2018; Quinde & Reinoso, 2016). Esta región experimenta una elevada frecuencia de terremotos, con aceleraciones máximas del suelo (PGA) que superan los 0.1g en gran parte del territorio (Cajamarca-Zuniga D. et al., 2022; MIDUVI, 2014c). Los eventos recientes, como el terremoto de Pedernales en 2016 (Mw 7.8), subrayan la vulnerabilidad de las infraestructuras y la importancia de considerar eventos sísmicos consecutivos en el diseño (Aguiar & Mieles, 2018; Mera et al., 2017; Velez & Romanel, 2021).
Adicionalmente, Ecuador ha implementado sistemas de aislamiento sísmico en infraestructuras críticas, como el hospital “Darío Machuca Palacios” en La Troncal y de Bahía de Caráquez (Guaraca et al., 2018; Morales et al., 2020), aunque el costo inicial limita su adopción a gran escala en Ecuador. En estructuras de hormigón armado, las estrategias de reforzamiento, como el hormigón reforzado con fibras de acero, han surgido como soluciones para mejorar la durabilidad y resistencia de edificaciones antiguas vulnerables (Avanaki & Dehghan, 2020; Perrault et al., 2020).
Dado el contexto sísmico ecuatoriano, evaluar la eficacia de sistemas estructurales alternativos como los pórticos arriostrados y los sistemas DIAGRID es fundamental para mejorar la seguridad y sostenibilidad de las edificaciones (Al Dughaishi et al., 2023). Investigaciones recientes sugieren que los sistemas DIAGRID, aunque tradicionalmente empleados en edificios altos (Nayak et al., 2020), son una opción viable y económica para edificios de mediana altura típicos de ciudades como Portoviejo (Asadi & Adeli, 2018). La comparación entre diferentes enfoques estructurales permitirá identificar el sistema más adecuado para las condiciones sísmicas locales, optimizando la relación costo-beneficio tanto en edificaciones nuevas como en la rehabilitación de estructuras existentes (Chango et al., 2024; Singh et al., 2023).
Aunque el sistema DIAGRID ha mostrado un comportamiento sísmico superior y ha requerido menores volúmenes de acero en comparación con los marcos a momento y los pórticos arriostrados en algunos estudios (Sukrawa et al., 2019), otras investigaciones han destacado la efectividad de los pórticos arriostrados concéntricamente en la resistencia a cargas laterales (Annan et al., 2009). Además, los desarrollos recientes en sistemas CBF, como los pórticos arriostrados concéntricamente con autocentrado (SC-CBF), han demostrado una mejor capacidad de deriva y desempeño sísmico en comparación con los sistemas CBF convencionales (Dyanati Mojtaba et al., 2014).
Este estudio se enfoca en una evaluación comparativa de la respuesta sísmica de los sistemas DIAGRID y SCBF en Portoviejo, Ecuador. A través de modelos numéricos y análisis lineales, se busca aportar datos que respalden la actualización de normativas de diseño y guíen a ingenieros y diseñadores en la selección de sistemas estructurales eficientes y seguros, promoviendo la adopción de tecnologías avanzadas que contribuyan a la mitigación del riesgo sísmico en Ecuador.
2. Metodología
2.1 Características de las Estructuras
Este estudio se centra en el análisis sísmico comparativo de un edificio de oficinas de 4 niveles de estructura metálica, ubicado en Portoviejo, Ecuador, considerando dos sistemas estructurales distintos: Pórticos Especiales a Momento Arriostrados Concéntricamente (PEMAC) y Pórticos Intermedios a Momento con Sistema Diagrid (PIMD). En esta ciudad es común la construcción de edificaciones de cuatro niveles; además, debido a la demanda sísmica de la región, se requiere el uso de estructuras livianas que puedan responder de manera eficiente a las fuerzas sísmicas.
Para el análisis, se desarrollaron dos modelos estructurales en programa especializado, ambos representando un edificio de cuatro niveles con dimensiones en planta de 24 x 15 metros, una altura de 4.0 m en el primer nivel y entrepisos de 3.6 m en los niveles superiores. Los modelos utilizan acero A36 en vigas, columnas y diagonales, mientras que para las losas y rellenos se emplea hormigón con una resistencia a la compresión de f ’c = 210 kg / cm2. Las cargas aplicadas en cada nivel se detallan en la Tabla 1 (MIDUVI, 2014b).
Tabla 1
Cargas aplicadas
Nivel |
Carga Permanente* kg/m2 |
Carga Viva kg/m2 |
Piso 1 a 3 |
488 |
240 |
Cubierta |
388 |
70 |
_______________________________
* Carga Muerta: El peso propio de la estructura se incluye de forma adicional y se calcula directamente en el software de análisis.
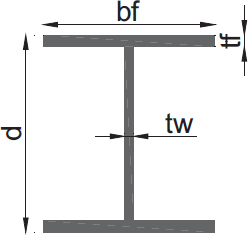
2.1.1 Modelo Matemático: Pórticos Especiales a Momento Arriostrados Concéntricamente (PEMAC)
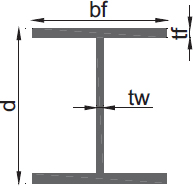
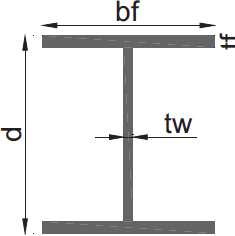
La Figura 1 muestra la configuración estructural, que incluye columnas y vigas con secciones tipo “I”, así como diagonales tubulares conectadas concéntricamente. Las losas con placas deck están dispuestas perpendicularmente a las vigas secundarias, alineándose con el eje corto de la estructura. Las vigas secundarias y principales, conectadas al eje débil de las columnas, se consideran como conexiones a corte y, por lo tanto, se analizan como vigas compuestas. En todos los niveles se integran diafragmas semirrígidos.
Figura 1
Configuración de modelo Sistema PEMAC: (a) Planta; (b) Elevación Eje 1; (c) Vista 3D
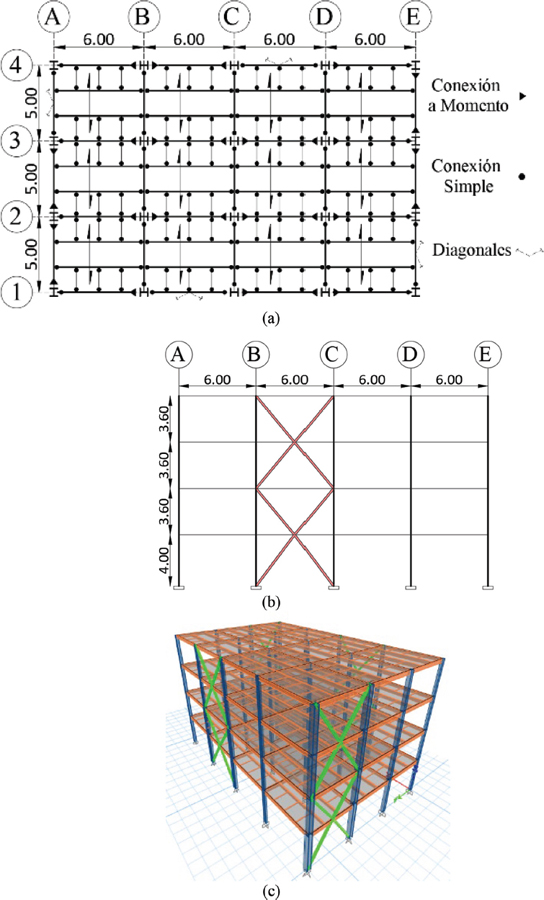
A continuación, se presentan las especificaciones detalladas de las secciones de columnas, vigas y diagonales utilizadas en el modelo estructural. Estas tablas contienen las dimensiones y características de cada elemento estructural, especificadas para los distintos niveles de la estructura.
La Tabla 2 muestra las secciones de columnas, clasificadas según su posición y altura dentro de la estructura. La Tabla 3 presenta las secciones de vigas principales y secundarias, diferenciadas por niveles, mientras que la Tabla 4 proporciona las dimensiones de las diagonales tubulares conectadas concéntricamente. Estos elementos han sido seleccionados para cumplir con los requisitos estructurales y de diseño acorde a normativas (American Institute of Steel Construction, 2016c, 2016b, 2016a; MIDUVI, 2014a).
Tabla 2
Secciones de columnas
EJES |
ID |
d |
tw |
bf |
tf |
|
mm |
mm |
mm |
mm |
|
||
N+4.00 / N+7.60 |
|
|||||
A1, D1, B4, E4 |
Col_A |
300 |
8 |
200 |
14 |
|
B1, C1, C4, D4 |
Col_F |
350 |
12 |
350 |
25 |
|
E1, E2, A4, A3 |
Col_H |
380 |
16 |
380 |
26 |
|
A2, B2, C2, D2, B3, C3, D3, E3 |
Col_B |
300 |
8 |
300 |
20 |
|
N+11.20 / N+14.80 |
||||||
A1, B4, E4, D1 |
Col_A |
300 |
8 |
200 |
14 |
|
B1, C1, C4, D4 |
Col_G |
350 |
8 |
200 |
14 |
|
E1, E2, A3, A4 |
Col_H |
380 |
16 |
380 |
26 |
|
E2, C2, D2, B3, C3, D3 |
Col_C |
300 |
6 |
180 |
10 |
|
A2, E3 |
Col_B |
300 |
8 |
300 |
20 |
|
Tabla 3
Secciones de vigas
EJES |
ID |
d |
tw |
bf |
tf |
|
mm |
mm |
mm |
mm |
|
||
N+4.00 / N+7.60 / N+11.20 |
|
|||||
1, 2, 3, 4 |
H |
300 |
6 |
130 |
10 |
|
A, E |
G |
320 |
6 |
160 |
10 |
|
B, C, D |
W |
320 |
8 |
210 |
12 |
|
N+14.80 |
||||||
1, 2, 3, 4 |
A |
280 |
5 |
130 |
10 |
|
A, E |
G |
320 |
6 |
160 |
10 |
|
B, C, D |
U |
320 |
6 |
170 |
12 |
|
Vigas secundarias |
||||||
Entrepisos / Cubierta |
Sec |
300 |
5 |
100 |
8 |
|
Tabla 4
Secciones de diagonales
EJES |
ID |
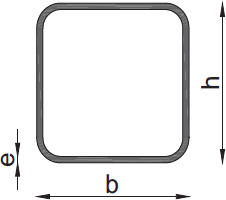
b |
h |
e |
|
mm |
mm |
mm |
|
||
N+4.00 |
|
||||
A3-A4, E1-E2, 1B-1C, 4C-4D |
DIAG 1 |
150 |
150 |
12 |
|
N+7.60 / N+11.20 / N+14.80 |
|||||
A3-A4, E1-E2, 1B-1C, 4C-4D |
DIAG 2 |
150 |
150 |
10 |
|
2.1.2 Modelo Matemático: Pórticos Intermedios a Momento con Sistema DIAGRID (PIMD)
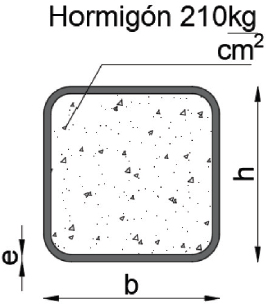
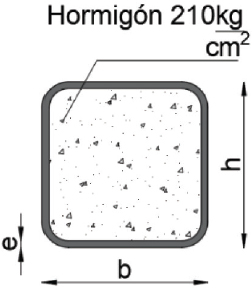
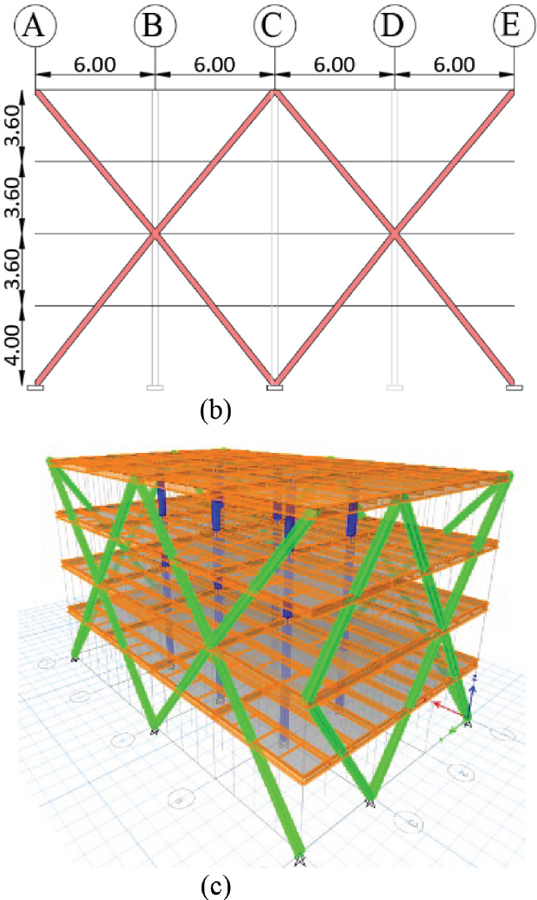
Este modelo, representado en la Figura 2, está compuesto por columnas tubulares cuadradas rellenas de hormigón, vigas de sección tipo I que forman el sistema principal para cargas gravitacionales y diagonales tipo DIAGRID, también formadas por tubos cuadrados rellenos de hormigón, diseñadas para controlar cargas laterales. Las consideraciones para las placas deck y las losas son idénticas a las empleadas en el sistema PEMAC.
Figura 2
Configuración de modelo Sistema PIMD: (a) Planta; (b) Elevación Eje 1; (c) Vista 3D
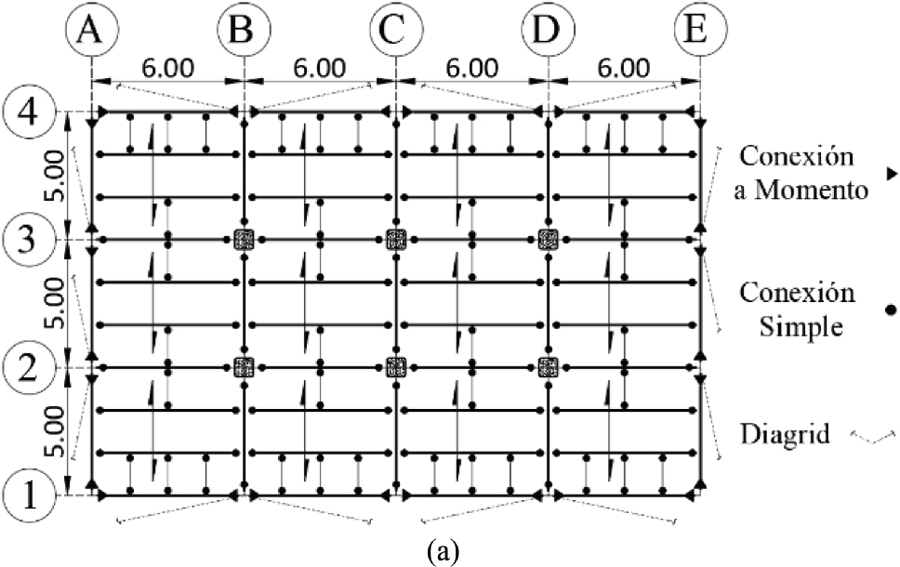
A continuación, se presentan las tablas con la nomenclatura y las especificaciones de las secciones utilizadas en las columnas, diagonales y vigas del modelo estructural. La Tabla 5 describe las secciones de las columnas a diferentes alturas, mientras que la Tabla 6 detalla las características de las vigas principales y secundarias en los distintos niveles de la estructura, incluyendo las dimensiones de sus secciones. Finalmente, la Tabla 7 proporciona las especificaciones de las diagonales DIAGRID empleadas para el control de cargas laterales.
Tabla 5
Secciones de columnas
EJES |
ID |
b |
h |
e |
|
mm |
mm |
mm |
|
||
N+4.00 / N+7.60 |
|
||||
B2, C2, D2, B3, C3, D3 |
Col_1 |
300 |
300 |
12 |
|
N+11.20 / N+14.80 |
|||||
B2, C2, D2, B3, C3, D3 |
Col_2 |
300 |
300 |
6 |
|
Tabla 6
Secciones de vigas
EJES |
ID |
d |
tw |
bf |
tf |
|
mm |
mm |
mm |
mm |
|
||
N+4.00 |
|
|||||
1, 4, A, E |
K |
375 |
8 |
150 |
12 |
|
B, C, D |
V |
365 |
8 |
150 |
10 |
|
2, 3 |
Z |
320 |
6 |
100 |
8 |
|
N+7.60 |
||||||
4A-B, 4D-E, 1A-B, 1D-E |
H |
400 |
7 |
200 |
14 |
|
A2-3, E2-3 |
Ñ |
430 |
14 |
215 |
22 |
|
A1-2, A3-4, E1-2, E3-4 |
J |
430 |
10 |
215 |
15 |
|
B1-2, C1-2, D1-2 B3-4, C3-4, D3-4 |
V |
365 |
8 |
150 |
10 |
|
B2-3, C2-3, D2-3 |
C |
345 |
6 |
150 |
10 |
|
2, 3 |
Z |
320 |
6 |
100 |
8 |
|
N+11.20 |
||||||
1, 4 |
M |
355 |
10 |
140 |
15 |
|
2, 3 |
Z |
320 |
6 |
100 |
8 |
|
A, E |
K |
375 |
8 |
150 |
12 |
|
B, C, D |
V |
365 |
8 |
150 |
10 |
|
N+14.80 |
||||||
A, E |
S |
400 |
8 |
205 |
15 |
|
4A-B, 4D-E, 1A-B, 1D-E |
H |
400 |
7 |
200 |
14 |
|
4B-C, 4C-D, 1B-C, 1C-D |
T |
400 |
10 |
200 |
16 |
|
B1-2, C1-2, D1-2 B3-4, C3-4, D3-4 |
L |
350 |
8 |
140 |
10 |
|
B2-3, C2-3, D2-3 |
P |
340 |
8 |
120 |
10 |
|
Vigas secundarias |
||||||
Entrepisos |
Sec |
290 |
5 |
100 |
8 |
|
Cubierta |
Sec Cub |
265 |
5 |
100 |
8 |
|
Tabla 7
Secciones de diagonales DIAGRID
EJES |
ID |
b |
h |
e |
|
mm |
mm |
mm |
|
||
N+4.00 / N+7.60 |
|
||||
A, E |
DIAG_1 |
300 |
300 |
15 |
|
1, 4 |
DIAG_2 |
300 |
300 |
8 |
|
N+11.20 / N+14.80 |
|||||
A, E |
DIAG_3 |
300 |
300 |
10 |
|
1, 4 |
DIAG_2 |
300 |
300 |
8 |
|
El material principal utilizado en la estructura es el acero A36, un tipo de acero al carbono ampliamente empleado en la industria de la construcción y fabricación de estructuras metálicas debido a su equilibrada combinación de resistencia, ductilidad y facilidad de fabricación. Como material complementario, se emplea hormigón simple con una resistencia a la compresión de f ’c = 210 kg / cm2, comúnmente utilizado en construcciones que no requieren altas resistencias. Este hormigón se utiliza en las losas sobre placas deck y para el relleno de las columnas y diagonales tipo DIAGRID. En la Tabla 8 se presenta las propiedades de los materiales.
Tabla 8
Propiedades de los materiales
Acero A36 |
Hormigón |
||
Esfuerzo de fluencia |
fy = 2531 kg / cm2 |
Resistencia a la compresión |
f ’c = 210 kg / cm2 |
Módulo de elasticidad |
Es = 2100000 kg / cm2 |
Módulo de elasticidad |
Ec = 218819.79 kg / cm2 |
Peso específico |
γs = 7850 kg / cm3 |
Peso específico |
γc = 2400 kg / cm3 |
2.2 Características del sitio
El suelo del casco urbano de Portoviejo está compuesto predominantemente por depósitos aluviales del río Portoviejo, consistentes en secuencias de capas de limos arcillosos con presencia de material limo arenoso (Hernández et al., 2019). La ciudad se encuentra en una zona sísmica VI, categorizada con un peligro sísmico muy alto (MIDUVI, 2014c). Para este estudio, se seleccionó un suelo tipo D, con una velocidad de onda cortante promedio (Vs30) entre 180 y 360 m/s, conforme a la normativa sísmica de Ecuador (MIDUVI, 2014c). En función de estas características, los coeficientes para la construcción del espectro de diseño se presentan en la Tabla 9.
Tabla 9
Características sísmicas del sitio
Tipo de Suelo |
Zona Sísmica |
Z |
Fa |
Fd |
Fs |
D |
VI |
0.50 |
1.12 |
1.11 |
1.40 |
2.3 Aspectos de Diseño Sismorresistente
De acuerdo con el tipo y función de la edificación, se adopta un factor de importancia sísmica de 1.0. Debido a su configuración estructural, se consideran irregularidades, para lo cual se estiman coeficientes de irregularidad en planta (ϕP = 1.00) e irregularidad en elevación (ϕE = 0.90). Para el modelo PEMAC, se establece un factor de modificación de respuesta R de 7, correspondiente a marcos especiales de acero arriostrados concéntricamente, según la normativa (American Society of Civil Engineers, 2017). En el caso del modelo PIMD, se basaron en investigaciones previas (Asadi & Adeli, 2018), las cuales recomiendan para edificios de baja altura (menos de 8 pisos) un factor R en el rango de 3.5 a 4. En este diseño, se optó por utilizar un factor R de 3.
El período de vibración de la estructura, Ta, se estima mediante los métodos establecidos en la normativa nacional (MIDUVI, 2014a). El primer método calcula el período T de forma aproximada mediante la ecuación (1), en la que se define Ct = 0.073 y α = 0.75, valores aplicables a estructuras de acero con arriostramientos (MIDUVI, 2014c).
En esta ecuación, Ct y α son coeficientes determinados por el tipo de edificación, mientras que hn representa la altura máxima del edificio. En este caso, el valor de período de referencia Ta es 0.55 segundos. Este valor se compara con el obtenido en el análisis dinámico, que considera las propiedades específicas de masa y rigidez lateral de cada modelo estructural.
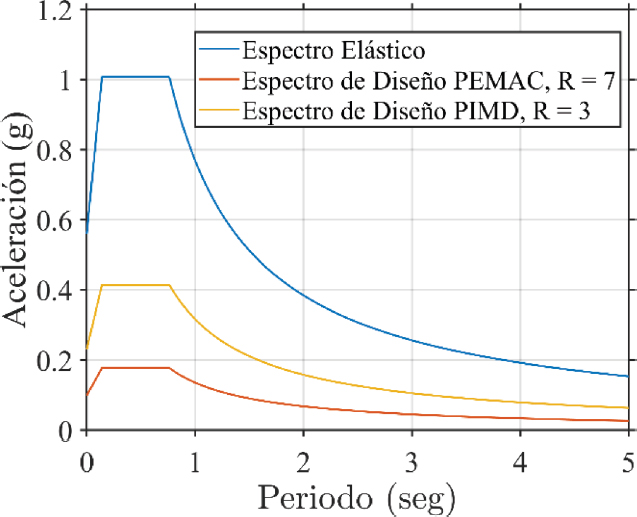
Los espectros de aceleración, tanto elásticos como inelásticos o de diseño, calculados en función de las características geotécnicas, sísmicas y del tipo de estructura, se muestran en la Figura 3.
Figura 3
Espectro de diseño para suelo D en Portoviejo
2.4 Análisis Sísmico
2.4.1 Cortante basal
El cortante basal de diseño (V) fue calculado según la ecuación 2 (MIDUVI, 2014c), utilizando el método estático equivalente. Los valores de cortante, considerando los sentidos de análisis x e y, para ambos modelos, PEMAC y PIMD, se encuentran en las Tabla 10, calculados con los factores de amplificación correspondientes y las características sísmicas del sitio.
Tabla 10
Cortante basal de diseño
Descripción |
T,s |
Sa, g |
R |
W, Ton |
Vx, % |
Vx, Ton |
Vy, % |
Vy, Ton |
PEMAC |
0.63 |
1.01 |
7 |
1016.50 |
16.00%W |
162.64 |
16.00%W |
162.64 |
PIMD |
0.38 |
1.01 |
3 |
1079.60 |
37.33%W |
403.06 |
37.33%W |
403.06 |
2.4.2 Análisis Modal Espectral
Para el análisis modal espectral, se incluyeron 12 modos de vibración, con 3 modos asignados por cada nivel. Se llevó a cabo la verificación del cortante basal mínimo respecto al método estático equivalente, la cual establece que el cortante basal dinámico debe alcanzar al menos el 80% del cortante basal estático. Los factores de escala (FSU1,2) se presentan en la Tabla 11.
Tabla 11
Factor de escala para el análisis modal espectral
Descripción |
FSU1 |
FSU2 |
PEMAC |
1.11 |
1.11 |
PIMD |
1.19 |
1.15 |
2.4.3 Desplazamientos y derivas
Los desplazamientos inelásticos δinel se determinan como se indica en la ecuación 3, incorporando un factor de amplificación del 8% debido a la ausencia de modelación de la reducción en los patines de las vigas, derivada de la conexión de sección reducida (RBS) (American Institute of Steel Construction, 2016a, p. 35; MIDUVI, 2014a).
Las derivas inelásticas se obtienen utilizando la expresión:
donde ΔE representa la deriva elástica. Para verificar el cumplimiento normativo, se comprueba que la deriva máxima calculada se mantenga dentro del límite permisible inelástico especificado (MIDUVI, 2014c). De acuerdo con esta normativa, para estructuras de hormigón armado, metálicas y de madera, la deriva máxima no debe exceder Δmax ≤ 0.02, expresándose como un porcentaje de la altura de cada piso.
2.4.4 Evaluación de la Capacidad de los Elementos
La capacidad de las columnas, vigas y diagonales se evaluó considerando las solicitaciones de fuerza axial, corte, momento y la interacción flexo-axial. Las secciones fueron diseñadas para cumplir con los requisitos establecidos en las normativas nacionales e internacionales pertinentes (American Institute of Steel Construction, 2016c, 2016b, 2016a; MIDUVI, 2014a), garantizando un desempeño estructural adecuado.
Por otra parte debido a la rigidez y capacidad de disipación de energía que ofrece el sistema PIMD, en su forma de malla diagonal, distribuyendo eficientemente las fuerzas sísmicas, el sistema DIAGRID permite que las estructuras mantengan su integridad sin grandes incursiones en el rango inelástico, incluso bajo cargas símicas fuertes (Ali & Moon, 2007).
2.5 Análisis Económico
El análisis económico de ambos modelos se realiza estimando el peso total de los materiales principales, acero y hormigón, utilizados en la estructura. Para ello, se emplearon los datos de resumen obtenidos del programa especializado, que incluyen las diferentes secciones de acero A36 y el peso del hormigón aplicado en las losas, los rellenos de los elementos DIAGRID y las columnas tubulares. La Tabla 12 presenta los precios unitarios considerados para el cálculo:
Tabla 12
Precio de Materiales. Fuente (Gad Portoviejo)
Material |
Unidad |
Precio Unitario |
Hormigón f ’c = 210 kg / cm2 |
m3 |
237.20 |
Suministro e instalación de acero estructural ASTM A36 con grúa |
kg |
3.35 |
3. Resultados
3.1 Comparación de Propiedades Dinámicas
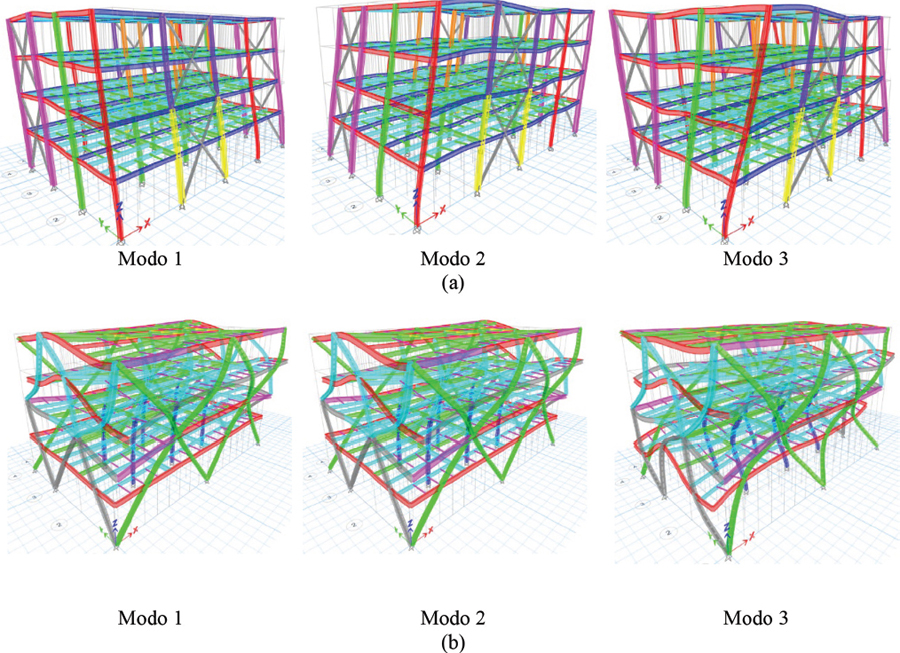
Los periodos de vibración fundamentales obtenidos para los modelos PEMAC y PIMD son de 0.63 s y 0.38 s, respectivamente. Esto indica una mayor rigidez lateral en el modelo PIMD, atribuida a la configuración DIAGRID, la cual podría mejorar significativamente el desempeño estructural frente a cargas laterales. En el modelo PEMAC, los primeros dos modos son traslacionales, seguidos de un tercer modo rotacional, mientras que en el modelo PIMD los primeros cuatro modos son traslacionales y la rotación se observa hasta el quinto modo. Esto confirma la eficacia del sistema DIAGRID en la mejora de la estabilidad de la estructura (ver Tabla 13 y Figura 4).
Tabla 13
Modos de vibrar para los modelos evaluados
Descripción |
Mode |
Period |
UX |
UY |
RZ |
S |
|||||
PEMAC |
1 |
0.63 |
0.0001 |
0.8325 |
0 |
2 |
0.58 |
0.8245 |
0.0001 |
0 |
|
3 |
0.37 |
0 |
0 |
0.8316 |
|
4 |
0.23 |
0.0005 |
0.1375 |
0 |
|
5 |
0.21 |
0.1404 |
0.0005 |
0 |
|
PIMD |
1 |
0.38 |
0.0068 |
0.6392 |
0 |
2 |
0.29 |
0.2828 |
0.0238 |
0 |
|
3 |
0.27 |
0.0343 |
0.2792 |
0 |
|
4 |
0.25 |
0.5503 |
0.011 |
0 |
|
5 |
0.22 |
0 |
0 |
0.1173 |
Figura 4
Modos de vibración para cada modelo: a) PEMAC; b) PIMD
3.2 Comparación de Cortante Basal en Direcciones X e Y
Los resultados de cortante basal en los modelos PEMAC y PIMD presentan diferencias significativas (ver Figura 5), atribuibles al factor de reducción sísmica (R) aplicado en cada sistema estructural. En el caso de la dirección X, el modelo PEMAC alcanza un cortante basal de diseño aproximado de 162 toneladas bajo carga estática y de 150 toneladas en análisis espectral, alcanzando un 92.99% de cortante basal dinámico con respecto al estático. En cambio, el modelo PIMD, con un diseño más rígido debido a su configuración de DIAGRID, muestra valores de 400 toneladas en el análisis estático y 335 toneladas en análisis espectral, logrando un 84.29% de cortante basal dinámico en comparación con el estático.
Figura 5
Cortante basal
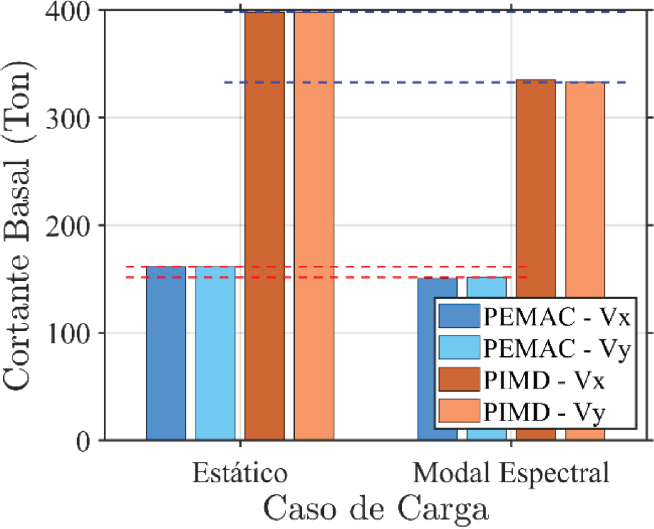
En la dirección Y, los valores de cortante basal muestran una tendencia similar. El modelo PEMAC presenta un cortante estático de 162 toneladas y espectral de 152 toneladas, con una relación del 93.80% de cortante basal dinámico respecto al estático. Por otro lado, el modelo PIMD obtiene un cortante estático de 400 toneladas y un valor espectral de 333 toneladas, con un 83.65% de cortante dinámico.
3.3 Capacidad axial de columnas gravitacionales
La capacidad de carga axial de las columnas muestra una diferencia significativa entre los tipos de columnas empleadas en los modelos PIMD y PEMAC, por ejemplo, en la columna central, que soporta las cargas gravitacionales principalmente. En el modelo PIMD, se utiliza una columna tubular metálica rellena de hormigón tipo HSS, cuya capacidad de carga axial (344.82 Ton) supera en aproximadamente un 8% a la columna de tipo IPE empleada en el modelo PEMAC (294.30 Ton).
3.4 Desplazamientos y derivas laterales
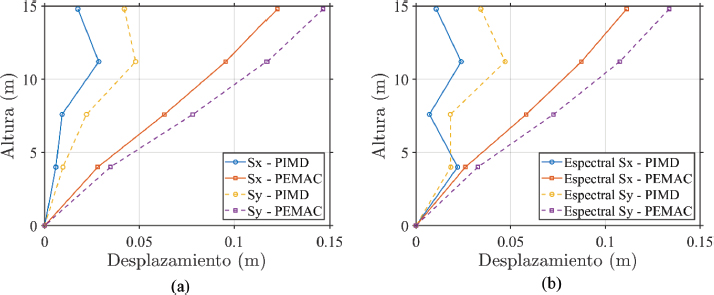
En la Figura 6 se presentan los desplazamientos inelásticos en las direcciones X e Y para ambos modelos (PIMD y PEMAC), destacando las diferencias en rigidez y deformación en función de la altura. La Figura 6(a) muestra los desplazamientos bajo el caso de carga estática equivalente, donde el modelo PIMD presenta desplazamientos máximos de aproximadamente 0.03 m en la dirección X y 0.05 m en la dirección Y, mientras que el modelo PEMAC alcanza hasta 0.12 m en X y 0.15 m en Y. En el análisis modal espectral, ilustrado en la Figura 6(b), el modelo PIMD exhibe desplazamientos de hasta 0.03 m en X y 0.05 m en Y, frente a los valores máximos de 0.11 m en X y 0.14 m en Y observados en el modelo PEMAC. Además, el modelo PIMD muestra una inclinación de línea menor y transiciones uniformes entre niveles, indicando una rigidez lateral superior y una distribución homogénea de deformaciones. Por el contrario, el modelo PEMAC presenta inclinaciones mayores y cambios irregulares en niveles superiores, sugiriendo una rigidez lateral decreciente y mayor susceptibilidad a deformaciones.
Figura 6
Desplazamientos inelásticos: a) Estático Equivalente; b) Modal Espectral
En la Figura 7 se presentan las derivas inelásticas. Se observa que el modelo PIMD mantiene derivas significativamente más bajas en comparación con el modelo PEMAC en ambas direcciones (X, Y) y para ambos casos de carga (Estático y Modal Espectral).
Figura 7
Derivas inelásticas: a) Estático Equivalente; b) Modal Espectral
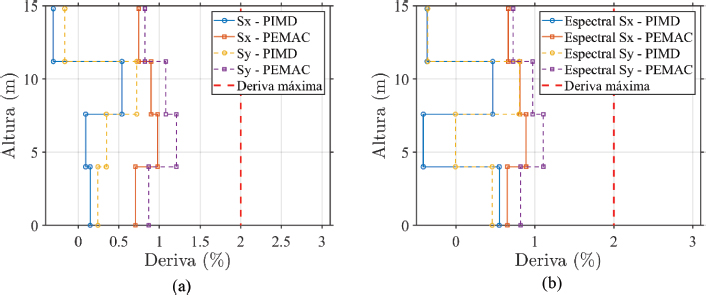
En el caso estático equivalente, las derivas máximas para el modelo PIMD alcanzan aproximadamente un 0.5% en la dirección X y un 0.8% en la dirección Y, mientras que el modelo PEMAC registra derivas más elevadas, alcanzando hasta 1.0% en X y 1.2% en Y. Estos valores sugieren que el modelo PIMD presenta una mayor rigidez lateral, reduciendo las deformaciones en cada nivel y manteniéndose por debajo del límite permisible de 2% (línea roja).
En el análisis modal espectral, el modelo PIMD también muestra derivas más controladas, con valores máximos cercanos a 0.55% en X y 0.8% en Y. En contraste, el modelo PEMAC alcanza derivas de aproximadamente 0.9% en X y 1.0% en Y, evidenciando nuevamente una menor rigidez lateral en comparación con el modelo PIMD.
3.5 Relación de Demanda versus Capacidad
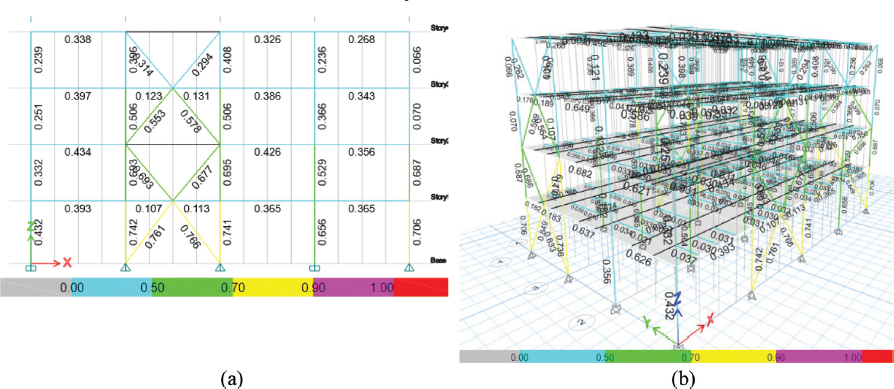
La fracción de demanda respecto a la capacidad (D/C) en el modelo PEMAC evidencia una distribución de cargas en la estructura con mayor concentración de esfuerzos en los pisos inferiores, la cual disminuye progresivamente hacia los niveles superiores. En el piso 1, las diagonales alcanzan relaciones D/C entre el 70% y 90%, mientras que en los pisos 2, 3 y 4, los esfuerzos en los arriostramientos concéntricos se mantienen por debajo del 70% de su capacidad (ver Figura 8). Esta tendencia también se observa en otros elementos estructurales como vigas y columnas.
Figura 8
Relación D/C del Sistema PEMAC: a) Pórtico Eje X, b) 3D
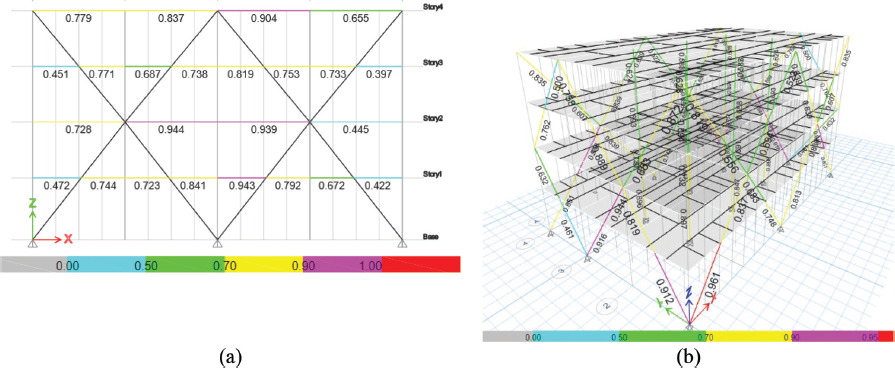
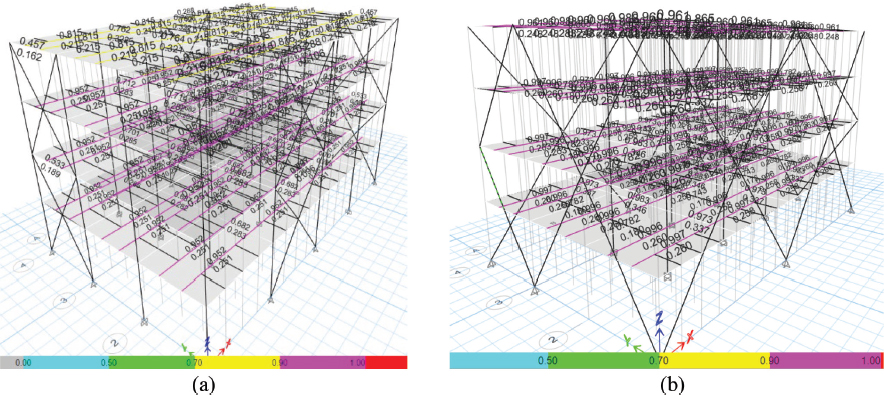
En el sistema PIMD, los esfuerzos presentan una distribución diferente, concentrándose en los pisos donde convergen las diagonales del sistema DIAGRID, específicamente en los niveles 2 y 4. Las vigas de estos pisos, así como de la cubierta, operan en un rango de D/C entre el 70% y 90%, mientras que las vigas de los niveles 1 y 3 muestran valores entre el 60% y 80% (ver Figura 9). Por otro lado, los elementos compuestos del sistema DIAGRID resisten de manera efectiva las cargas laterales, con relaciones D/C que varían entre el 80% y 95% en los dos primeros pisos, y entre el 60% y 80% en los niveles 3 y 4.
Figura 9
Relación D/C del Sistema PIMD: a) Pórtico Eje X, b) 3D
La Figura 10 presenta la relación D/C para las vigas secundarias en los sistemas evaluados. En el sistema PEMAC, las vigas secundarias alcanzan valores elevados de D/C, con algunos tramos que superan el 0.9, evidenciando un nivel de esfuerzo cercano a su capacidad máxima, especialmente en los pisos inferiores. En el caso del sistema PIMD, los valores de D/C también se aproximan a 1.0, principalmente en los niveles donde convergen los elementos DIAGRID, lo que indica una mayor demanda estructural en estas zonas.
Figura 10
Relación D/C de vigas secundarias: a) Sistema PEMAC, b) Sistema PIMD
3.5.1 Relación D/C Casos Especiales Modelo PEMAC
En los marcos arriostrados, se consideran dos casos de carga fundamentales para el diseño por capacidad (American Institute of Steel Construction, 2016b; MIDUVI, 2014a). El Caso 1 abarca la evaluación de las fuerzas esperadas en las diagonales, considerando tanto los esfuerzos de compresión como de tracción, basados en la capacidad de los elementos arriostrados bajo condiciones extremas. Este caso permite verificar que los nudos y sus conexiones resistan adecuadamente estas fuerzas, garantizando la estabilidad estructural.
El Caso 2 se centra en comparar las fuerzas esperadas a tracción y la capacidad a compresión en las diagonales con las fuerzas desarrolladas tras el pandeo del elemento, es decir, una vez que las diagonales alcanzan su capacidad máxima y experimentan deformaciones post-pandeo. Este análisis es clave para asegurar que las secciones de vigas y columnas posean suficiente resistencia y rigidez para evitar fallas prematuras, incluso cuando los elementos arriostrados se encuentran en un estado degradado.
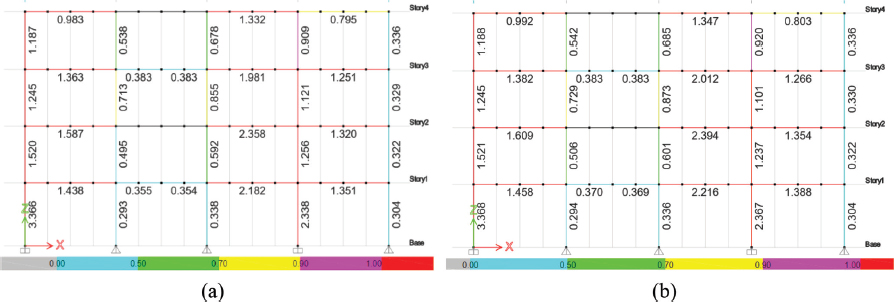
La inclusión de ambos casos permite una evaluación exhaustiva del probable desempeño de los marcos arriostrados bajo diferentes estados de carga, cumpliendo con los criterios de diseño por capacidad y asegurando que la demanda no exceda la capacidad disponible del sistema (ver Figura 11).
Figura 11
Relación D/C marcos arriostrados del modelo PEMAC: a) Caso 1, b) Caso 2
3.6 Reacciones en los apoyos
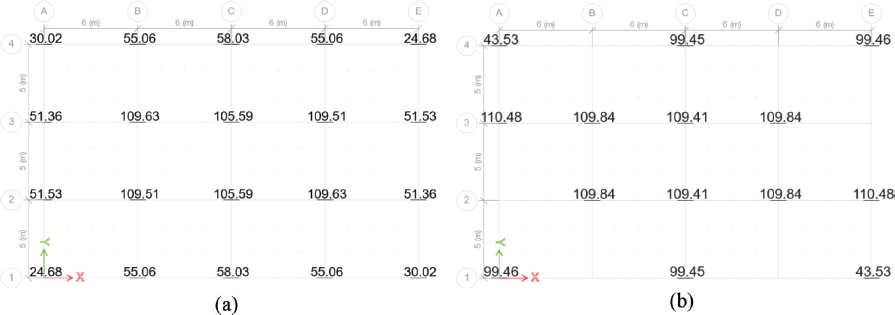
Las reacciones generadas por las cargas de servicio (carga viva y carga muerta), desempeñan un papel importante en el diseño de las fundaciones estructurales. Como se muestra en la Figura 12, aunque ambos modelos (PEMAC y PIMD) transmiten pesos globales similares al suelo, existen diferencias en la distribución de las cargas. En el modelo PEMAC, las reacciones máximas en los puntos de soporte alcanzan valores de 109.53 Ton en el eje central (B), mientras que en el modelo PIMD, las reacciones son más uniformes, alcanzando valores de hasta 110.48 Ton en el eje E. Esta uniformidad en el modelo PIMD permite diseñar cimentaciones similares para los apoyos.
Figura 12
Reacciones en la base: a) PEMAC; b) PIMD
3.7 Peso propio de la estructura
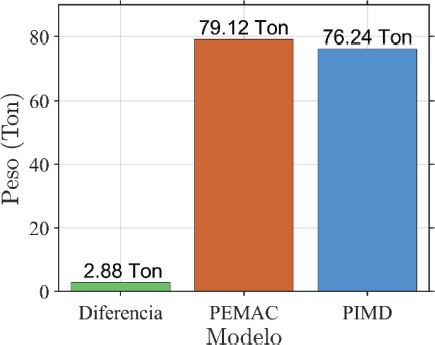
Un objetivo clave en el diseño sismorresistente es lograr estructuras ligeras pero seguras, con capacidad suficiente para resistir los eventos sísmicos de la región. La reducción de la masa sísmica se convierte en un aspecto fundamental para mejorar el comportamiento estructural, y por ello, se evaluó el peso de los materiales principales en cada modelo. La Figura 13 muestra la relación del peso de los elementos de acero de ambos modelos. El modelo PEMAC tiene un peso total de 79.12 toneladas, mientras que el modelo PIMD alcanza 76.24 toneladas, logrando una reducción de 2.88 toneladas en el peso propio.
Figura 13
Peso de acero
3.8 Análisis Comparativo de Costos de Construcción
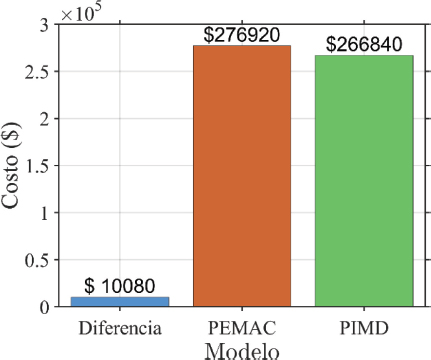
Para este análisis, se consideraron los costos de provisión y montaje del acero estructural A36, excluyendo los costos adicionales de cimentaciones, mamposterías, revestimientos y acabados. Tras realizar la comparación, se observa que el modelo PIMD permite un ahorro significativo en el costo total de construcción (Figura 14). El modelo PEMAC presenta un costo de $276,920.00, mientras que el modelo PIMD alcanza un costo de $266,840.00, lo que representa una diferencia de $10,080.00, es decir, un ahorro del 3.64% a favor del modelo PIMD.
Figura 14
Costo de estructura de acero
4. Conclusiones
El sistema PIMD demostró una rigidez lateral significativamente superior en comparación con el sistema PEMAC. Esto se refleja en los menores períodos de vibración obtenidos, así como en los desplazamientos y derivas laterales reducidas. La configuración Diagrid distribuye de manera uniforme las fuerzas laterales a lo largo de la estructura, lo que minimiza las deformaciones y asegura un comportamiento más eficiente bajo cargas sísmicas. El análisis modal reveló que el sistema PIMD posee modos de vibración traslacionales dominantes en los primeros modos, con menores contribuciones rotacionales en comparación con el sistema PEMAC. Esto demuestra una mejor respuesta dinámica, lo que resulta en una mayor estabilidad estructural y un comportamiento más predecible bajo la acción de cargas sísmicas.
El sistema PIMD mostró una concentración de esfuerzos en pisos específicos, lo que podría generar puntos críticos de fallo que requieren especial atención en el diseño y detallado estructural. Si bien esta concentración de esfuerzos puede comprometer ciertos elementos bajo cargas extremas, el presente análisis no incluyó la evaluación del desempeño de las conexiones, aspecto que queda fuera del alcance de este estudio. Para garantizar una adecuada disipación de energía y mejorar el comportamiento global de la estructura, se recomienda abordar el diseño detallado de las conexiones en estudios futuros, incluyendo pruebas experimentales para validar y optimizar los resultados obtenidos.
El modelo PIMD logró una reducción del 3.64% en el consumo de acero en comparación con el modelo PEMAC, manteniendo o incluso mejorando el desempeño estructural en términos de derivas, relaciones demanda-capacidad y comportamiento modal. Esta optimización se refleja en un ahorro significativo en los costos de construcción, lo que posiciona al sistema PIMD como una alternativa eficiente y económicamente viable para edificaciones de acero en zonas de alta sismicidad, sin comprometer la seguridad estructural.
La evaluación realizada confirma que el sistema DIAGRID (PIMD) es una alternativa estructural robusta y eficiente para edificaciones de baja altura en zonas de alta sismicidad, como Portoviejo. Su implementación podría mejorar el desempeño sísmico sin incrementar de manera significativa los costos de construcción, presentándose como una opción técnica y económicamente viable para futuras edificaciones en la región.
Referencias
Aguiar, R., & Mieles, Y. (2018). Análisis de los edificios que colapsaron en Portoviejo durante el terremoto del 16 de abril de 2016. Revista Internacional de Ingeniería de Estructuras, 21(3), 257-282. https://doi.org/10.24133/riie.v21i3.601
Al Dughaishi, H., Al Lawati, J., Alosta, M., Mahmood, S., Al-Kazee, M. F., Yusoff, N. I., & Milad, A. (2023). Analysis and Design of Lateral Framing Systems for Multi-Story Steel Buildings. Applied Mechanics, 4(2), 389-406. https://doi.org/10.3390/applmech4020022
Ali, M. M., & Moon, K. S. (2007). Structural Developments in Tall Buildings: Current Trends and Future Prospects. Architectural Science Review, 50(3), 205-223. https://doi.org/10.3763/asre.2007.5027
American Institute of Steel Construction. (2016a). Prequalified Connections for Special and Intermediate Steel Moment Frames for Seismic Applications (ANSI/AISC 358-16). American Institute of Steel Construction. https://www.aisc.org/products/publication/historic-standards/prequalified-connections/prequalified-connections-ansiaisc-358-16-with-ansiaisc-358s1-18-and-ansiaisc-358s2-202/
American Institute of Steel Construction. (2016b). Seismic Provisions for Structural Steel Buildings (ANSI/AISC 341-16). American Institute of Steel Construction. https://www.aisc.org/products/publication/historic-standards/seismic-provisions/seismic-provisions-for-structural-steel-buildings-ansiaisc-341-16-download/
American Institute of Steel Construction. (2016c). Specification for Structural Steel Buildings (ANSI/AISC 360-16). American Institute of Steel Construction. https://www.aisc.org/products/publication/historic-standards/specification-for-structural-steel-buildings/specification-for-structural-steel-buildings-ansiaisc-360-16-download/
American Society of Civil Engineers. (2017). Minimum design loads and associated criteria for buildings and other structures.
Annan, C. D., Youssef, M. A., & El Naggar, M. H. (2009). Experimental evaluation of the seismic performance of modular steel-braced frames. Engineering Structures, 31(7), 1435-1446. https://doi.org/10.1016/j.engstruct.2009.02.024
Asadi, E., & Adeli, H. (2018). Nonlinear Behavior and Design of Mid- to High-Rise Diagrid Structures in Seismic Regions. Engineering Journal, 55(3), 161-180. https://doi.org/10.62913/engj.v55i3.1135
Avanaki, M. J., & Dehghan, A. (2020). Seismic performance of steel fiber reinforced concrete segmented lining tunnels. En Tunnels and Underground Cities: Engineering and Innovation Meet Archaeology, Architecture and Art (pp. 5685-5691). CRC Press.
Beauval, C., Marinière, J., Yepes, H., Audin, L., Nocquet, J.‐M., Alvarado, A., Baize, S., Aguilar, J., Singaucho, J.‐C., & Jomard, H. (2018). A New Seismic Hazard Model for Ecuador. Bulletin of the Seismological Society of America, 108(3A), 1443-1464. https://doi.org/10.1785/0120170259
Bigonah, M., Haidar Ali, B., Rashed, P., & Li, S. (2024). Automatic evaluation of progressive collapse performance of braced frames. Engineering Failure Analysis, 166, 108892. https://doi.org/10.1016/j.engfailanal.2024.108892
Bilham, R. (2010). Lessons from the Haiti earthquake. Nature, 463(7283), 878-879. https://doi.org/10.1038/463878a
Cajamarca-Zuniga D., Kabantsev O. V., & Marin C. (2022). Macroseismic intensity-based catalogue of earthquakes in Ecuador. Structural Mechanics of Engineering Constructions and Buildings, 18(2), 161-171. https://doi.org/10.22363/1815-5235-2022-18-2-161-171
Carrillo, J., Hernández-Barrios, H., & Rubiano-Fonseca, A. (2014). Analysis of the Earthquake-Resistant Design Approach for Buildings in Mexico. Ingeniería. Investigación y Tecnología, XV(1), 151-162. Redalyc.
Chandra Dutta, S., Halder, L., & Prasad Sharma, R. (2021). Seismic vulnerability assessment of low to mid-rise RC buildings addressing prevailing design and construction practices in the Northeastern region of the Indian subcontinent: A case study based approach. Structures, 33, 1561-1577. https://doi.org/10.1016/j.istruc.2021.05.032
Chango, B., Ruiz, K., Hernández, L., & Baquero, R. (2024). Estudio comparativo del uso de columnas de acero huecas y columnas compuestas en pórticos resistentes a momento. Ciencia, Ingenierías y Aplicaciones, 7(1), 33-54. https://doi.org/10.22206/cyap.2024.v7i1.3122
Chen, W., & Zhang, L. (2022). An automated machine learning approach for earthquake casualty rate and economic loss prediction. Reliability Engineering & System Safety, 225, 108645. https://doi.org/10.1016/j.ress.2022.108645
Dyanati Mojtaba, Huang Qindan, & Roke David A. (2014). Structural and Nonstructural Performance Evaluation of Self-Centering, Concentrically Braced Frames under Seismic Loading. En Structures Congress 2014 (pp. 2393-2404). https://doi.org/10.1061/9780784413357.210
Goda, K., Kiyota, T., Pokhrel, R. M., Chiaro, G., Katagiri, T., Sharma, K., & Wilkinson, S. (2015). The 2015 Gorkha Nepal Earthquake: Insights from Earthquake Damage Survey. Frontiers in Built Environment, 1. https://www.frontiersin.org/journals/built-environment/articles/10.3389/fbuil.2015.00008
Guaraca, F. X. C., Guevara, B. A. F., & Calero, Ing. J. F. V., M. Sc. (2018). Análisis no lineal de la estructura del Hospital Darío Machuca Palacios del cantón La Troncal en Ecuador. KnE Engineering, 3(2), 292-300. https://doi.org/10.18502/keg.v3i1.1434
Hernández, E. H. O., Sánchez, L. K. M., & Gutiérrez, D. A. D. (2019). Evaluación del subsuelo, y su comportamiento geotécnico en el Cantón Portoviejo, parroquia 12 de marzo. Revista Caribeña de Ciencias Sociales (RCCS), 12, 67.
Kinik, F. (2023, abril 22). 50,783 people confirmed dead in Türkiye earthquakes. https://www.aa.com.tr/en/turkiye/50-783-people-confirmed-dead-in-turkiye-earthquakes/2878735
Lu, X., Lu, X., Guan, H., & Xie, L. (2016). Application of earthquake-induced collapse analysis in design optimization of a supertall building. The Structural Design of Tall and Special Buildings, 25(17), 926-946. https://doi.org/10.1002/tal.1291
Mera, W., Vera, X., La Tegola, A., & Ponce, G. (2017). April 2016 Ecuador Earthquake of Moment Magnitude Mw7.8: Overview and Damage Report. Key Engineering Materials, 747, 662-669. https://doi.org/10.4028/www.scientific.net/KEM.747.662
MIDUVI. (2014a). NEC-SE-AC: Norma Ecuatoriana de la Construcción – Estructuras de Acero. Ministerio de Desarrollo Urbano y Vivienda. https://www.habitatyvivienda.gob.ec/documentos-normativos-nec-norma-ecuatoriana-de-la-construccion/
MIDUVI. (2014b). NEC-SE-CG: Norma Ecuatoriana de la Construcción – Cargas (no sísmicas). Ministerio de Desarrollo Urbano y Vivienda. https://www.habitatyvivienda.gob.ec/documentos-normativos-nec-norma-ecuatoriana-de-la-construccion/
MIDUVI. (2014c). NEC-SE-DS: Norma Ecuatoriana de la Construcción – Seguridad Estructural – Diseño Sismo Resistente. Ministerio de Desarrollo Urbano y Vivienda. https://www.habitatyvivienda.gob.ec/documentos-normativos-nec-norma-ecuatoriana-de-la-construccion/
Morales, E., Cagua, B., Pilatasig, J., Kitayama, S., & Romo, M. (2020). Seismic performance assessment of the seismically isolated Bahía de Caraquez Hospital. The 17th World Conference on Earthquake Engineering. World Conference on Earthquake Engineering, Japón. https://wcee.nicee.org/wcee/article/17WCEE/2g-0276.pdf
Nayak, C., Walke, S., & Kokare, S. (2020). Optimal Structural Design of Diagrid Structure for Tall Structure. En V. K. Gunjan, S. N. Singh, T. Duc-Tan, G. J. Rincon Aponte, & A. Kumar (Eds.), ICRRM 2019 – System Reliability, Quality Control, Safety, Maintenance and Management (pp. 263-271). Springer Singapore.
Ozturk, M., Arslan, M. H., & Korkmaz, H. H. (2023). Effect on RC buildings of 6 February 2023 Turkey earthquake doublets and new doctrines for seismic design. Engineering Failure Analysis, 153, 107521. https://doi.org/10.1016/j.engfailanal.2023.107521
Perrault, M., Guéguen, P., Parra, G., & Sarango, J. (2020). Modification of the data-driven period/height relationship for buildings located in seismic-prone regions such as Quito (Ecuador). OAI_1. https://doc.cerema.fr/Default/doc/OAI_1/oai-HAL-hal-04322120v1/modification-of-the-data-driven-period-height-relationship-for-buildings-located-in-seismic-prone-re
Quinde, P., & Reinoso, E. (2016). Estudio de peligro sísmico de Ecuador y propuesta de espectros de diseño para la Ciudad de Cuenca. Ingeniería sísmica, 94. https://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S0185-092X2016000100001
Singh, H., Tiwary, A. K., Thakur, S., & Thakur, G. (2023). Performance evaluation of high-rise reinforced concrete buildings under dynamic loading considering different structural systems. Materials Today: Proceedings. https://doi.org/10.1016/j.matpr.2023.08.251
Sukrawa, M., Pringgana, G., & Sanjaya, P. D. T. (2019). Comparative analysis and design of tower using diagrid, conventional moment frame and braced frame system of steel structures. MATEC Web of Conferences, 276, 01026. https://doi.org/10.1051/matecconf/201927601026
Tena-Colunga, A., & Hernández-Ramírez, H. (2020). Resilient seismic design of steel frames with hysteretic fuses in a code-oriented format. Journal of Building Engineering, 32, 101768. https://doi.org/10.1016/j.jobe.2020.101768
Terán-Gilmore, A., Roeslin, S., Tapia-Hernández, E., & Cuadros-Hipólito, E. (2021). Displacement-based design of tall earthquake-resistant diagrid systems. Journal of Building Engineering, 35, 102022. https://doi.org/10.1016/j.jobe.2020.102022
The human cost of disasters: An overview of the last 20 years (2000-2019). | UNDRR. (2020, octubre 12). https://www.undrr.org/publication/human-cost-disasters-overview-last-20-years-2000-2019
Velez, D., & Romanel, C. (2021). Dynamic Numerical Analysis of the Mazar Concrete Faced Rockfill Dam in Ecuador – South America. En M. Barla, A. Di Donna, & D. Sterpi (Eds.), Challenges and Innovations in Geomechanics (pp. 710-717). Springer International Publishing.
_______________________________
1 Universidad Técnica de Manabí, Ecuador. Ingeniero Civil. Maestrante Académico. ORCID: 0009-0007-8576-1333. Correo-e: gpico8433@utm.edu.ec.
2 Universidad Técnica de Manabí, Ecuador. Profesor invitado en el Programa de Maestría Trayectoria Profesional en Ingeniería Civil Mención Estructuras. Magister en Ingeniería Civil con Mención en Estructuras. ORCID: 0000-0003-2530-8549. Correo-e: brian.cagua.g@gmail.com.