Ciencia, Ingenierías y Aplicaciones, Vol. 7, No. 2, julio-diciembre, 2024 ISSN (impreso): 2636-218X • ISSN (en línea): 2636-2171
DESARROLLO DE UNA ECUACIÓN PARA EL CÁLCULO DEL FACTOR DE FRICCIÓN EN ACCESORIOS Y PIEZAS ESPECIALES
Development of a Friction Factor Correlation for Fittings and Special Components
DOI: https://doi.org/10.22206/cyap.2024.v7i2.3216
Recibido: 4/7/2024 • Aceptado: 1/11/2024
Cómo citar: Meléndez Valencia, M., García Maimó, J., Mariano-Hernández, D., Aybar-Mejía, M. (2024). Desarrollo de una ecuación para el cálculo del factor de fricción en accesorios y piezas especiales. Ciencia, Ingenierías y Aplicaciones, 7(2), 111-135. https://doi.org/10.22206/cyap.2024.v7i2.3216
Resumen
En el presente trabajo se desarrolló una ecuación para calcular el factor de fricción para piezas especiales (codos, reducciones de tuberías, llaves de paso) y accesorios (válvulas, difusores de presión, calentadores) utilizando la ecuación de Darcy-Weisbach para obtener un valor estimado de las pérdidas de energía que se tienen cuando un fluido a cierta velocidad y con cierta viscosidad pasa a través de accesorios o piezas especiales. Para llegar a la ecuación se propuso partir de las premisas que toda pérdida de energía por fricción de un fluido es causada por la velocidad, pero se refleja en la presión. Además, se asumió que los accesorios y piezas especiales siempre trabajan en turbulencia total. Para esta investigación se utilizó ingeniería inversa a lo que normalmente se hace al calcular el factor de fricción para las piezas especiales y accesorios que consiste en utilizar el Diagrama de Moody (1944) para estos fines. El diagrama de Moody tiene como abscisa los valores del Número de Reynolds que definen el régimen de velocidad (turbulencia o laminar) de un fluido obteniendo de forma gráfica el valor de fricción. Para desarrollar la ecuación se buscó el valor del factor de fricción para cada valor en mil de Reynolds. Utilizando MATLAB se construyeron varias curvas y se analizó el porcentaje de error versus el diagrama de Moody. La ecuación que tuvo un error de aproximación de fracciones racionales (RAT2) por debajo de 0.99.
Palabras clave: Factor de fricción; diagrama de Moody; flujo laminar; flujo turbulento; MATLAB.
Abstract
In the present work, an equation was developed that can calculate the friction factor (fT) for special parts (elbows, pipe reductions, stopcocks) and accessories (valves, pressure diffusers, heaters) using the Darcy-Weisbach equation to obtain an estimate value of the energy losses that occur when a fluid at a certain speed and with a certain viscosity passes through fittings or special parts. To arrive at the equation, it was proposed to start from the premises that any loss of energy due to friction of a fluid is caused by velocity but is reflected in pressure. In addition, accessories and special parts always work in total turbulence. For this research, reverse engineering was used to calculate the friction factor for special parts and accessories, which consists of using the Moody Diagram (1944) for these purposes. The Moody diagram has as an abscissa the values of the Reynolds Number that define the velocity regime (turbulence or laminar) of a fluid, obtaining the friction value graphically. To develop the equation, the value of fT for each Reynolds value in thousand was sought. Using MATLAB, several curves were constructed, and the error percentage was analyzed against the Moody's chart. The equation that had a Rational Fraction Approximation (RAT2) error below 0.99.
Keywords: Friction factor; Moody's chart; laminar flow; turbulent flow; MATLAB.
1. Introducción
La necesidad de transportar fluidos a través de tuberías es de vital importancia, sobre todo cuando la aplicación es transportar agua potable, gasoductos, oleoductos, gas domiciliario en las ciudades. Se han desarrollado ecuaciones para el cálculo de las variables involucradas en el transporte de fluidos a través de tuberías (Mandavgane, 2020). El desarrollo de las ecuaciones de flujo está directamente ligado con las necesidades, siempre cambiantes, del hombre (Singh et al., 2017). Las primeras ecuaciones fueron desarrolladas para el cálculo de las variables involucradas en el diseño de sistemas de distribución de agua, la cual era transportada a través de canales abiertos. Con la potabilización de esta y el riesgo de su contaminación en los canales, se generaron ecuaciones para el flujo de agua en tuberías (Huilier, 2019).
La aparición de las industrias impulsó las investigaciones que tenían por objeto desarrollar ecuaciones que pudiera aplicarse a fluidos diferentes al agua y en una amplia variedad de condiciones de operación, con lo cual se pasó de las ecuaciones empíricas a aproximaciones, ecuaciones y gráficas semi-racionales, que reemplazaron las expresiones empíricas antes utilizadas. Sin embargo, un gran porcentaje de los ingenieros de diseño, usan las ecuaciones sin tener claridad con respecto a sus limitaciones y a la correcta selección de los parámetros requeridos para que los resultados obtenidos estén de acuerdo con la realidad (Gunadi et al., 2018). Los ingenieros que diseñan sistemas de distribución de fluidos se enfrentan a alguno de los tres problemas que se presentan a continuación (Levenspiel, 2007):
•Conocido el flujo a transportar, la energía disponible y la rugosidad, calcular el diámetro de la tubería.
•Conocido el diámetro, la rugosidad y la energía disponible, calcular el flujo que puede transportarse.
•Conocido el diámetro, la rugosidad y el flujo a transportarse, determinar las pérdidas de energía en el sistema.
Esto ha conllevado una serie de ecuaciones y soluciones parciales o totales que de alguna manera describen, en la mayoría de los casos, aspectos fundamentales de su desarrollo que dan cierta claridad a sus alcances y a sus limitaciones. Hasta el momento, todavía se usan gráficos para obtener factores necesarios en el cálculo de gastos energéticos en accesorios, reducciones y piezas especiales (Plascencia et al., 2020).
Tener programas que calculen todas las variables aún se hace impráctico, por lo cual se depende del gráfico de Moody para poder obtener de forma gráfica el factor de fricción a utilizar para un accesorio. Debido a esto, es necesario el desarrollo de una ecuación que permita de forma analítica poder obtener valores de los factores de fricción para accesorios, acodamientos y piezas especiales. El objetivo de este artículo es presentar una ecuación para el cálculo del factor de fricción en accesorios y piezas especiales de una tubería utilizando como base el Diagrama de Moody.
2. Antecedentes
El estudio de las pérdidas de fricción en accesorios y piezas especiales no es tan complicado como para tuberías sometidas a flujos turbulentos (Roberson & Crowe, 2000). Las tuberías sometidas a flujo turbulento y fluctuaciones aleatorias de cada componente de velocidad y el termino de presión en la ecuación de Darcy-Weisbach hacen que el análisis exacto sea muy difícil aun utilizando métodos numéricos para obtener el factor de fricción (Agudelo Martínez & Arango Ramírez, 2018).
Las tuberías están sometidas a tres zonas diferentes que complican de sobremanera el cálculo de la fricción en las tuberías:
1.Régimen turbulento tuberías lisas
2.Régimen turbulento intermedio
3.Régimen turbulento en tuberías rugosas
Por esta razón para el cálculo de pérdidas en tuberías se tienen diversas ecuaciones para la obtención del factor de fricción dependiendo si las tuberías son lisas y su grado de turbulencia (Anaya-Durand et al., 2013). Por ejemplo, la ecuación Colebrooks-White (Ecuación 1) y la ecuación de Karman-Prandlt (Ecuación 2) para regímenes turbulentos:
Donde, f es el factor de fricción para tuberías, NR es el número de Reynolds, D es el diámetro de la tubería y ε es rugosidad interna de la tubería.
Existe una numerosa cantidad de ecuaciones para calcular el factor de fricción en el cálculo de fricción en tuberías, siendo la más comunes las citadas anteriormente. De igual forma, existe otro método utilizado para la obtención del factor de fricción para tuberías, tanto para regímenes laminares como para regímenes turbulento, el cual es el diagrama de Moody. Este diagrama fue utilizado por mucho tiempo, por la complejidad que se tenía en utilizar las ecuaciones teóricas. Sin embargo, la revolución tecnológica y los diversos programas numéricos han hecho que el uso de las ecuaciones vuelva a ser de uso cotidiano (Camaraza Medina, 2011).
El diagrama de Moody es una representación gráfica en una escala doblemente logarítmica del factor de fricción en función del número de Reynolds y la rugosidad relativa de una tubería. Este diagrama fue realizado por Lewis Ferry Moody basándose en la ecuación de Darcy-Weisbach principalmente para la parte turbulenta del diagrama. El cálculo del factor de fricción utilizando el diagrama de Moody se define en función de dos parámetros como son el Número de Reynolds y la rugosidad relativa de una tubería, que es el cociente entre la rugosidad interna de la tubería y su diámetro.
El diagrama de Moody es aplicable a fluidos incompresibles (como agua). La forma de utilización del diagrama de Moody es conociendo el valor del Número de Reynolds en el eje de las abscisas, se traza una línea vertical por este número y donde intercepte con una de las curvas que existen para cada valor del parámetro, su proyección hacia la ordenada indica el valor del factor de fricción para ese flujo que se tiene en la tubería con su determinado régimen (Iturbide et al., 2017). Una vez obtenido el factor de fricción para la tubería y el régimen correspondiente, utilizando la ecuación de Darcy-Weisbach, se obtiene las pérdidas de energía por fricción que tendrá ese fluido en ese tramo de tubería (Shah & London, 1978).
En la Figura 1 se presenta el diagrama de Moody aplicado para analizar factor de fricción en función del número de Reynolds y la rugosidad relativa de una tubería.
Figura 1
Diagrama de Moody (Moody, 1944; Brown, 2002)
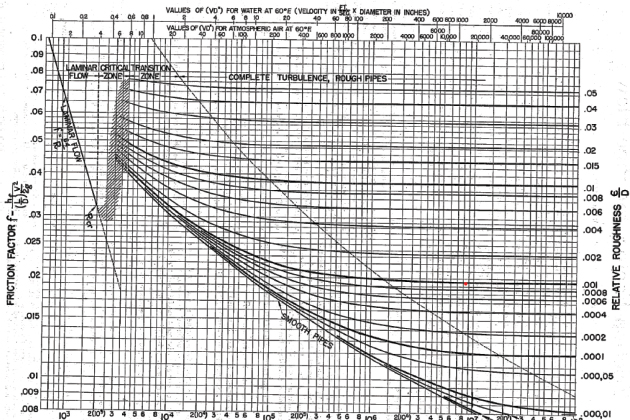
Al referirnos a pérdidas menores están asociadas al flujo de fluidos en un sistema de tuberías, y son causadas, por ejemplo, por una válvula que se utiliza para regular el flujo de un caudal por una tubería. Esto se logra cambiando totalmente la geometría del sistema (abriendo o cerrando más o menos la válvula), la cual está asociada a una perdida por fricción que se produce dentro de la válvula debido a la fricción que sucede dentro de ella al cambiar su geometría interna (Mandavgane, 2020).
Estas pérdidas de energía pueden ser muy altas en el sistema completo, por lo que su cálculo se hace imprescindible. Las pérdidas de energía son proporcionales a la carga de velocidad cuando estos pasan a través de un accesorio y pieza especial (Melendez, 2016). En estos casos las pérdidas de energía (Batista de Lima et al., 2015), se calculan con la Ecuación 3:
donde K es el coeficiente de resistencia, v es la velocidad al cuadrado y g la gravedad.
En el caso del coeficiente de resistencia es adimensional debido a que representa una constante de proporcionalidad entre la perdida de energía y la carga de velocidad. Por lo que la magnitud va a depender de la geometría del dispositivo que ocasiona la perdida, y a veces de la velocidad de flujo (Miller, 1996). En algunos casos especiales como son las expansiones o contracciones súbitas, el valor de K es igual a la Ecuación 4:
donde (Le/D) se denomina longitud equivalente, y es la longitud de una tubería recta del mismo diámetro nominal que el de la válvula (Fernández Bolaños & Pérez Cristancho, 2010). fT es el factor de fricción en la tubería a la que está conectada la válvula o acoplamiento, y que se da por hecho que está en la zona de turbulencia completa (Diehl, 2023).
El valor (Le/D), llamado relación de longitud equivalente, se considera constante para un tipo dado de válvula o acoplamiento. El termino (fT) es el factor de fricción en la tubería a la que está conectada la válvula o acoplamiento, que se da por hecho que está en la zona de turbulencia completa. Los valores para fT varían según el tamaño de la tubería y la válvula, lo que hace que el valor del coeficiente de resistencia K también varié.
En la Tabla 1 se muestra la resistencia de válvulas y acoplamiento expresadas como longitud equivalente en diámetros de tuberías.
Tabla 1
Resistencia de válvulas y acoplamiento
Accesorio |
Le/D* |
Codo 45 |
16 |
Codo 90 |
30 |
Codo roscado |
50 |
Codo radio largo |
20 |
Codo mitre |
60 |
Tee estándar con flujo directo |
20 |
Tee con flujo hacia el ramal |
60 |
Válvula de compuerta abierta al 100% |
8 |
Válvula de compuerta abierta al 75% |
35 |
Válvula de compuerta abierta al 50% |
160 |
Válvula de compuerta abierta al 25% |
900 |
Válvula de globo |
340 |
Válvula de ángulo |
55 |
Válvula verificación |
100 |
Válvula verificación tipo bola |
150 |
Válvula de mariposa 2 a 8 pulg. diámetro |
45 |
Válvula de mariposa 10 a 14 pulg. diámetro |
35 |
Válvula de mariposa 16 a 24 pulg. diámetro |
25 |
Válvula check horizontal |
600 |
Válvula check vertical con alcachofa |
420 |
* Le/D igual a longitud equivalente en diámetros de tuberías.
Los valores para fT varían según el tamaño de la tubería y la válvula, lo que hace que el valor del coeficiente de resistencia K también varié. El valor de fT se obtiene utilizando el número de Reynolds de la tubería anterior al accesorio y utilizando solamente la curva denominada de turbulencia completa (ver Figura 2), que además es la única curva con trazos discontinuos, que tiene el diagrama (Florescu et al., 2012). Las pérdidas por fricción en los accesorios no son calculadas, sino que se asume como un porcentaje de las pérdidas de fricción de las tuberías.
Figura 2
Diagrama de Moody resaltando la curva de turbulencia total (Moody, 1944)
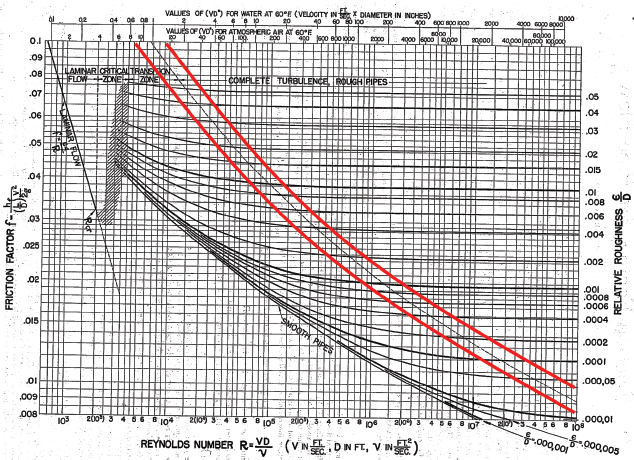
3. Desarrollo y Validación de la Ecuación
El objetivo principal de este trabajo es obtener una ecuación relativamente sencilla que pueda ser integrada a los cálculos de pérdidas para los sistemas de tuberías a presión, y permitir de estimar los mismos. Los Pasos que se realizaron fueron:
1.Tomando la curva de turbulencia total del diagrama de Moody y los diferentes Números de Reynolds (mayores de 6000), obtener el valor del factor de fricción para accesorios y piezas especiales (ver Figura 3).
2.Con esos números de fT y los números de Reynolds utilizando MATLAB, obtener una o varias ecuaciones que satisfaga los valores de fT y proponer la que tenga el menor error (rat 1) como la ecuación para obtener el valor de fT (ver Tabla 2).
Figura 3
Diagrama de Moody resaltando los valores del factor de fricción (Moody, 1944)
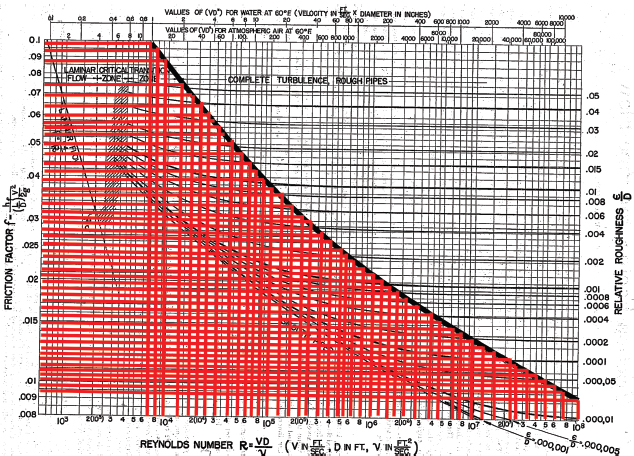
Tabla 2
Valores del factor de fricción para la curva de turbulencia total obtenidos del gráfico de Moody
Número Reynolds |
Factor de Friccion |
Número Reynolds |
Factor de Friccion |
6,000 |
0.1 |
900,000 |
0.022 |
7,000 |
0.093 |
1,000,000 |
0.021 |
8,000 |
0.090 |
2,000,000 |
0.018 |
9,000 |
0.086 |
3,000,000 |
0.017 |
10,000 |
0.084 |
4,000,000 |
0.016 |
20,000 |
0.065 |
5,000,000 |
0.015 |
30,000 |
0.056 |
6,000,000 |
0.014 |
40,000 |
0.052 |
7,000,000 |
0.014 |
50,000 |
0.046 |
8,000,000 |
0.014 |
60,000 |
0.044 |
9,000,000 |
0.013 |
70,000 |
0.042 |
10,000,000 |
0.013 |
80,000 |
0.040 |
20,000,000 |
0.012 |
90,000 |
0.038 |
30,000,000 |
0.011 |
100,000 |
0.038 |
40,000,000 |
0.011 |
200,000 |
0.032 |
50,000,000 |
0.010 |
300,000 |
0.027 |
60,000,000 |
0.010 |
400,000 |
0.026 |
70,000,000 |
0.010 |
500,000 |
0.025 |
80,000,000 |
0.010 |
600,000 |
0.024 |
90,000,000 |
0.009 |
700,000 |
0.023 |
100,000,000 |
0.009 |
800,000 |
0.022 |
|
|
El presente trabajo presenta una ecuación tomada desde la curva discontinua para cada valor del número de Reynolds correspondiente, y utilizando MATLAB, llegar a una ecuación que describa dicha curva y así obtener en función del Número de Reynolds y la curva discontinua el factor de fricción para accesorios y piezas especiales (Agudelo Martínez & Arango Ramírez, 2018). En la Figura 4 se muestra los valores de la curva de turbulencia total de la ecuación propuesta, donde el eje x represente el factor de fricción en la tubería mientras que el eje y representa el número de Reynolds para ambos casos las unidades que se presentan son adimensionales.
Figura 4
Gráfico de los valores de la curva de turbulencia total en MATLAB
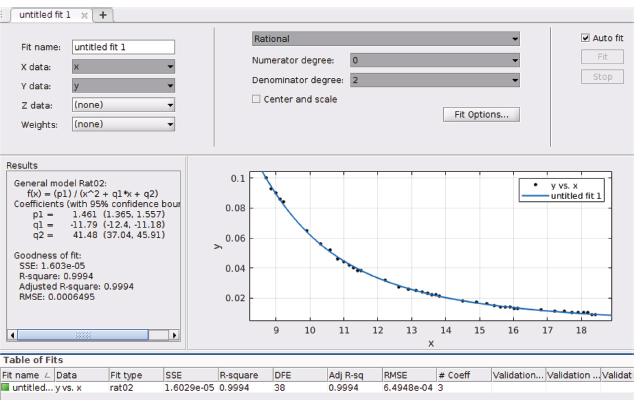
En la Tabla 3 se presentan los resultados obtenidos de la Ecuación 5 con una primera aproximación en MATLAB de la interpolación de la curva de turbulencia total del Diagrama de Moody.
Tabla 3
Resultados de la Ecuación 5
Número Reynolds |
fT Moody |
Valor fT |
Diferencial con Moody |
6,000 |
0.1 |
0.100 |
-0.27% |
7,000 |
0.093 |
0.095 |
-1.77% |
8,000 |
0.090 |
0.090 |
0.02% |
9,000 |
0.086 |
0.086 |
-0.10% |
10,000 |
0.084 |
0.083 |
1.52% |
20,000 |
0.065 |
0.064 |
1.77% |
30,000 |
0.056 |
0.055 |
1.72% |
40,000 |
0.052 |
0.050 |
4.74% |
50,000 |
0.046 |
0.046 |
0.24% |
60,000 |
0.044 |
0.043 |
2.14% |
70,000 |
0.042 |
0.041 |
2.76% |
80,000 |
0.040 |
0.039 |
2.36% |
90,000 |
0.038 |
0.038 |
1.11% |
100,000 |
0.038 |
0.036 |
3.27% |
200,000 |
0.032 |
0.029 |
9.25% |
300,000 |
0.027 |
0.026 |
3.50% |
400,000 |
0.026 |
0.024 |
7.73% |
500,000 |
0.025 |
0.023 |
7.58% |
600,000 |
0.024 |
0.022 |
8.04% |
700,000 |
0.023 |
0.021 |
9.83% |
800,000 |
0.022 |
0.020 |
8.49% |
900,000 |
0.022 |
0.020 |
9.03% |
1,000,000 |
0.021 |
0.019 |
9.16% |
2,000,000 |
0.018 |
0.016 |
9.40% |
3,000,000 |
0.017 |
0.015 |
9.56% |
4,000,000 |
0.016 |
0.014 |
10.95% |
5,000,000 |
0.015 |
0.013 |
11.23% |
6,000,000 |
0.014 |
0.013 |
10.29% |
7,000,000 |
0.014 |
0.013 |
11.62% |
8,000,000 |
0.014 |
0.012 |
10.76% |
9,000,000 |
0.013 |
0.012 |
11.90% |
10,000,000 |
0.013 |
0.012 |
11.98% |
20,000,000 |
0.012 |
0.010 |
13.79% |
30,000,000 |
0.011 |
0.009 |
16.58% |
40,000,000 |
0.011 |
0.009 |
15.53% |
50,000,000 |
0.010 |
0.009 |
12.24% |
60,000,000 |
0.010 |
0.009 |
9.85% |
70,000,000 |
0.010 |
0.009 |
8.89% |
80,000,000 |
0.010 |
0.009 |
5.11% |
90,000,000 |
0.009 |
0.009 |
1.00% |
100,000,000 |
0.009 |
0.009 |
0.02% |
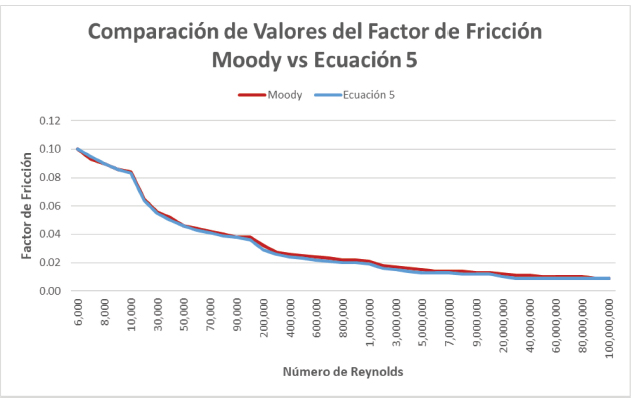
En la Figura 5 se presenta la comparación de los valores de fricción para la curva de turbulencia entre el Gráfico de Moody y la Ecuación 5.
Figura 5
Comparación de valores de factor de fricción entre el gráfico de Moody y la Ecuación 5
En la Tabla 4 se presentan los resultados obtenidos de graficar los datos de la curva de turbulencia total del Diagrama de Moody y con la función matemática de Excel se obtuvo la Ecuación 6.
Tabla 4
Resultados de la Ecuación 6
Número Reynolds |
fT Moody |
Valor fT |
Diferencial con Moody |
6,000 |
0.1 |
0.1084 |
-7.81% |
7,000 |
0.093 |
0.1112 |
-16.40% |
8,000 |
0.090 |
0.1136 |
-20.83% |
9,000 |
0.086 |
0.1158 |
-25.77% |
10,000 |
0.084 |
0.1178 |
-28.71% |
20,000 |
0.065 |
0.1311 |
-50.45% |
30,000 |
0.056 |
0.1391 |
-59.75% |
40,000 |
0.052 |
0.1447 |
-64.08% |
50,000 |
0.046 |
0.1490 |
-69.13% |
60,000 |
0.044 |
0.1524 |
-71.14% |
70,000 |
0.042 |
0.1552 |
-72.95% |
80,000 |
0.040 |
0.1576 |
-74.63% |
90,000 |
0.038 |
0.1597 |
-76.21% |
100,000 |
0.038 |
0.1614 |
-76.78% |
200,000 |
0.032 |
0.1717 |
-81.36% |
300,000 |
0.027 |
0.1761 |
-84.67% |
400,000 |
0.026 |
0.1784 |
-85.43% |
500,000 |
0.025 |
0.1796 |
-86.37% |
600,000 |
0.024 |
0.1803 |
-86.97% |
700,000 |
0.023 |
0.1806 |
-87.27% |
800,000 |
0.022 |
0.1807 |
-87.83% |
900,000 |
0.022 |
0.1806 |
-88.10% |
1,000,000 |
0.021 |
0.1804 |
-88.36% |
2,000,000 |
0.018 |
0.1763 |
-89.80% |
3,000,000 |
0.017 |
0.1720 |
-90.41% |
4,000,000 |
0.016 |
0.1682 |
-90.67% |
5,000,000 |
0.015 |
0.1648 |
-90.90% |
6,000,000 |
0.014 |
0.1619 |
-91.17% |
7,000,000 |
0.014 |
0.1593 |
-91.21% |
8,000,000 |
0.014 |
0.1570 |
-91.40% |
9,000,000 |
0.013 |
0.1548 |
-91.41% |
10,000,000 |
0.013 |
0.1529 |
-91.50% |
20,000,000 |
0.012 |
0.1396 |
-91.77% |
30,000,000 |
0.011 |
0.1317 |
-91.65% |
40,000,000 |
0.011 |
0.1261 |
-91.67% |
50,000,000 |
0.010 |
0.1218 |
-91.79% |
60,000,000 |
0.010 |
0.1183 |
-91.80% |
70,000,000 |
0.010 |
0.1154 |
-91.69% |
80,000,000 |
0.010 |
0.1129 |
-91.77% |
90,000,000 |
0.009 |
0.1108 |
-91.88% |
100,000,000 |
0.009 |
0.1089 |
-91.74% |
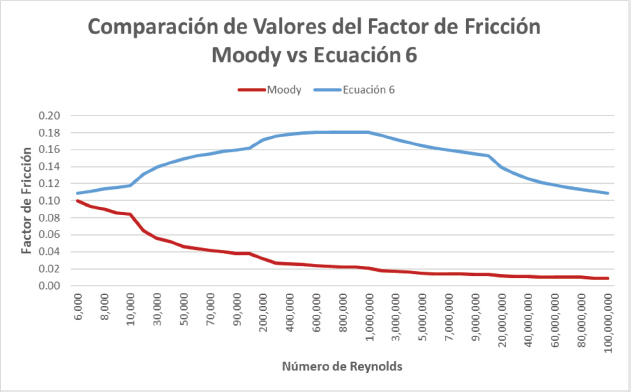
En la Figura 6 se presenta la comparación de los valores de fricción para la curva de turbulencia entre el Gráfico de Moody y la Ecuación 6.
Figura 6
Comparación de valores de factor de fricción entre el gráfico de Moody y la Ecuación 6
En la Tabla 5 se presentan los resultados obtenidos de la Ecuación 7 con una segunda aproximación en MATLAB de la interpolación de la curva de turbulencia total del Diagrama de Moody.
Tabla 5
Resultados de la Ecuación 7
Número Reynolds |
fT Moody |
Valor fT |
Diferencial con Moody |
6,000 |
0.1 |
0.0995 |
0.47% |
7,000 |
0.093 |
0.0938 |
-0.89% |
8,000 |
0.090 |
0.0892 |
0.85% |
9,000 |
0.086 |
0.0854 |
0.67% |
10,000 |
0.084 |
0.0821 |
2.20% |
20,000 |
0.065 |
0.0644 |
0.87% |
30,000 |
0.056 |
0.0563 |
-0.58% |
40,000 |
0.052 |
0.0513 |
1.25% |
50,000 |
0.046 |
0.0478 |
-3.95% |
60,000 |
0.044 |
0.0452 |
-2.83% |
70,000 |
0.042 |
0.0432 |
-2.81% |
80,000 |
0.040 |
0.0415 |
-3.67% |
90,000 |
0.038 |
0.0401 |
-5.25% |
100,000 |
0.038 |
0.0388 |
-3.57% |
200,000 |
0.032 |
0.0319 |
0.12% |
300,000 |
0.027 |
0.0286 |
-5.74% |
400,000 |
0.026 |
0.0265 |
-2.10% |
500,000 |
0.025 |
0.0250 |
-2.28% |
600,000 |
0.024 |
0.0239 |
-1.83% |
700,000 |
0.023 |
0.0230 |
-0.14% |
800,000 |
0.022 |
0.0222 |
-1.26% |
900,000 |
0.022 |
0.0216 |
-0.67% |
1,000,000 |
0.021 |
0.0211 |
-0.46% |
2,000,000 |
0.018 |
0.0179 |
0.54% |
3,000,000 |
0.017 |
0.0163 |
1.09% |
4,000,000 |
0.016 |
0.0153 |
2.56% |
5,000,000 |
0.015 |
0.0145 |
2.89% |
6,000,000 |
0.014 |
0.0140 |
2.03% |
7,000,000 |
0.014 |
0.0135 |
3.25% |
8,000,000 |
0.014 |
0.0131 |
2.41% |
9,000,000 |
0.013 |
0.0128 |
3.42% |
10,000,000 |
0.013 |
0.0125 |
3.34% |
20,000,000 |
0.012 |
0.0109 |
5.28% |
30,000,000 |
0.011 |
0.0100 |
9.08% |
40,000,000 |
0.011 |
0.0095 |
10.07% |
50,000,000 |
0.010 |
0.0091 |
9.38% |
60,000,000 |
0.010 |
0.0088 |
9.81% |
70,000,000 |
0.010 |
0.0085 |
11.84% |
80,000,000 |
0.010 |
0.0083 |
11.06% |
90,000,000 |
0.009 |
0.0081 |
9.83% |
100,000,000 |
0.009 |
0.0080 |
11.96% |
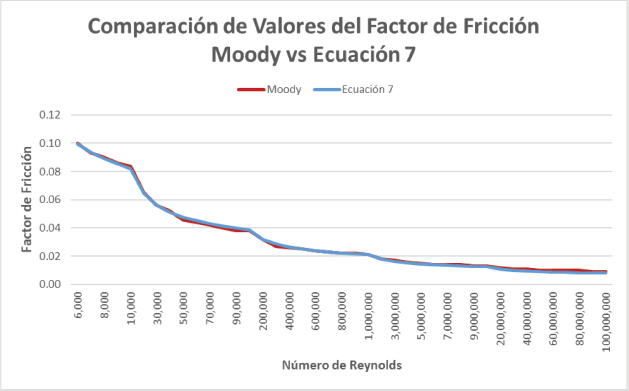
En la Figura 7 se presenta la comparación de los valores de fricción para la curva de turbulencia entre el Gráfico de Moody y la Ecuación 7.
Figura 7
Comparación de valores de factor de fricción entre el gráfico de Moody y la Ecuación 7
En la Tabla 6 se presentan los resultados obtenidos de la Ecuación 8 con una tercera aproximación en MATLAB de la interpolación de la curva de turbulencia total del Diagrama de Moody.
Tabla 6
Resultados de la Ecuación 8
Número Reynolds |
fT Moody |
Valor fT |
Diferencial con Moody |
6,000 |
0.1 |
0.0989 |
1.07% |
7,000 |
0.093 |
0.0934 |
-0.51% |
8,000 |
0.090 |
0.0889 |
1.14% |
9,000 |
0.086 |
0.0852 |
0.94% |
10,000 |
0.084 |
0.0819 |
2.50% |
20,000 |
0.065 |
0.0635 |
2.25% |
30,000 |
0.056 |
0.0549 |
1.96% |
40,000 |
0.052 |
0.0496 |
4.83% |
50,000 |
0.046 |
0.0458 |
0.23% |
60,000 |
0.044 |
0.0431 |
2.06% |
70,000 |
0.042 |
0.0409 |
2.64% |
80,000 |
0.040 |
0.0391 |
2.21% |
90,000 |
0.038 |
0.0376 |
0.94% |
100,000 |
0.038 |
0.0363 |
3.09% |
200,000 |
0.032 |
0.0293 |
9.18% |
300,000 |
0.027 |
0.0260 |
3.66% |
400,000 |
0.026 |
0.0240 |
8.16% |
500,000 |
0.025 |
0.0226 |
8.25% |
600,000 |
0.024 |
0.0215 |
8.96% |
700,000 |
0.023 |
0.0207 |
11.00% |
800,000 |
0.022 |
0.0200 |
9.87% |
900,000 |
0.022 |
0.0194 |
10.64% |
1,000,000 |
0.021 |
0.0189 |
10.97% |
2,000,000 |
0.018 |
0.0159 |
13.01% |
3,000,000 |
0.017 |
0.0143 |
14.64% |
4,000,000 |
0.016 |
0.0133 |
17.40% |
5,000,000 |
0.015 |
0.0126 |
18.91% |
6,000,000 |
0.014 |
0.0120 |
19.03% |
7,000,000 |
0.014 |
0.0115 |
21.55% |
8,000,000 |
0.014 |
0.0110 |
21.65% |
9,000,000 |
0.013 |
0.0107 |
23.91% |
10,000,000 |
0.013 |
0.0104 |
24.83% |
20,000,000 |
0.012 |
0.0084 |
35.93% |
30,000,000 |
0.011 |
0.0074 |
47.26% |
40,000,000 |
0.011 |
0.0068 |
53.06% |
50,000,000 |
0.010 |
0.0064 |
54.94% |
60,000,000 |
0.010 |
0.0061 |
57.14% |
70,000,000 |
0.010 |
0.0059 |
60.66% |
80,000,000 |
0.010 |
0.0058 |
59.32% |
90,000,000 |
0.009 |
0.0057 |
56.70% |
100,000,000 |
0.009 |
0.0056 |
58.36% |
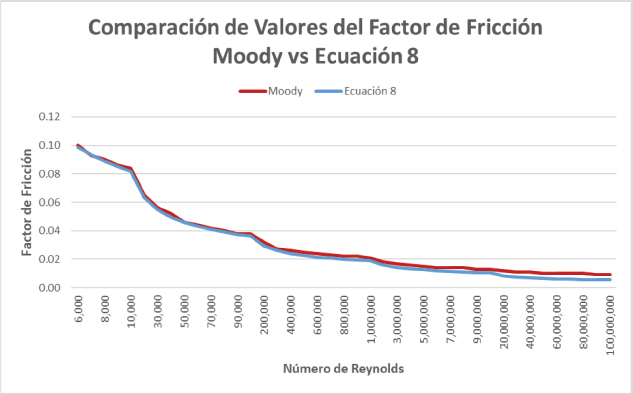
En la Figura 8 se presenta la comparación de los valores de fricción para la curva de turbulencia entre el Gráfico de Moody y la Ecuación 8.
Figura 8
Comparación de valores de factor de fricción entre el gráfico de Moody y la Ecuación 8
La ecuación 7 es a nuestro juicio la que mejor precisión tiene (ver Figura 5) y la que menor RAT tienen de todas y de acuerdo con los matemáticos consultados. Una función racional (RAT1) es un ajuste igual de bueno que el polinomio de grado 4 (ver Ecuación 9) que habría involucrado 4 parámetros en vez de los 5 del caso del polinomio de grado 4.
Donde, a =141, b = -3.354 y se corresponde con fm y x con el logaritmo del NR.
Para validar la ecuación se solicitó a dos compañías diseñadoras de sistemas sanitarios para viviendas que hicieran un análisis de las pérdidas por accesorios con la ecuación que presentamos versus el sistema que ellos normalmente utilizan (ver Tabla 7). La empresa A asume normalmente un porcentaje de las pérdidas por fricción de las tuberías como perdidas por accesorios. Dependiendo del diseño ellos asumen entre un 15 y un 35%.
Tabla 7
Estimación de la perdida por accesorio usando la formula desarrollada
Pieza |
D (pulg) |
D (m) |
Le/D |
V (m/s) |
V2/2g (m) |
Densidad (kg/m3) |
N (pas*s) |
Nr |
ft |
K |
hk (m) |
hk (psi) |
C1 |
1/2 |
0.0127 |
30 |
0.96 |
0.0469 |
998.91 |
1.12E-03 |
10864.15 |
0.08 |
2.39 |
0.11 |
0.16 |
C2 |
1/2 |
0.0127 |
30 |
0.96 |
0.0469 |
998.91 |
1.12E-03 |
10864.15 |
0.08 |
2.39 |
0.11 |
0.16 |
C3 |
1/2 |
0.0127 |
30 |
0.96 |
0.0469 |
998.91 |
1.12E-03 |
10864.15 |
0.08 |
2.39 |
0.11 |
0.16 |
C4 |
1/2 |
0.0127 |
30 |
0.96 |
0.1456 |
998.91 |
1.12E-03 |
19125.43 |
0.07 |
1.96 |
0.29 |
0.41 |
C5 |
1/2 |
0.0127 |
30 |
1.69 |
0.1456 |
998.91 |
1.12E-03 |
19125.43 |
0.07 |
1.96 |
0.29 |
0.41 |
C6 |
1/2 |
0.0127 |
30 |
1.69 |
0.0469 |
998.91 |
1.12E-03 |
10864.15 |
0.08 |
2.39 |
0.11 |
0.16 |
C7 |
1/2 |
0.0127 |
30 |
0.96 |
0.0469 |
998.91 |
1.12E-03 |
10864.15 |
0.08 |
2.39 |
0.11 |
0.16 |
T1 |
1/2 |
0.0127 |
20 |
0.96 |
0.0469 |
998.91 |
1.12E-03 |
10864.15 |
0.08 |
1.60 |
0.07 |
0.11 |
T2 |
3/4 |
0.0190 |
20 |
0.96 |
0.1899 |
998.91 |
1.12E-03 |
32762.20 |
0.05 |
1.09 |
0.21 |
0.30 |
a |
Estimación con la formula propuesta |
1.42 |
2.01 |
|||||||||
b |
Estimación con REVIT |
0.82 |
1.16 |
|||||||||
c |
Diferencia entre la ecuacion propuesta y el software REVIT |
0.60 |
0.85 |
|||||||||
d |
Diferencia porcentual |
73.63% |
||||||||||
Realizando la comparación, para el diseño que ellos analizaron utilizaron un 30% de las pérdidas por fricción en las tuberías. Utilizando la ecuación propuesta el % de pérdidas estuvo en el 36% de las pérdidas por tubería, y de acuerdo con sus conclusiones, además de ya no ser una suposición, sino que permite saber de forma matemática el valor de las pérdidas, también permite localizar los puntos y/o zonas de mayor perdida por accesorios.
La empresa B utilizó un software REVIT2023 de AUTODESK, al realizar el cálculo de la diferencia porcentual entre los valores obtenidos existe una diferencia de un 73.63%, sin embargo, aunque se aprecia una diferencia alta en términos de valores reales, la diferencia es de 0.60 m por encima de lo que midió el REVIT2023.
Además de estas dos empresas diseñadoras se hizo un trabajo de comparación entre los estudiantes de Ingeniería Hidráulica II, del Instituto Tecnológico de Santo Domingo (junio 2023 a enero 2024), durante tres trimestres, donde comparamos las pérdidas de los accesorios, se asumió un 15% de las pérdidas por fricción de las tuberías, las pérdidas calculadas utilizando el grafico de Moody y la ecuación presentada (ver Tabla 8). La ecuación resulta en aproximadamente 30% más que las pérdidas por fricción en las tuberías. Utilizando el diagrama de Moody, la comparación con la ecuación propuesta es similar, pero expresado por los estudiantes, la ecuación reduce el tiempo de cálculo, sustancialmente.
Tabla 8
Comparación entre la Ecuación 7 y el Diagrama de Moody
|
Perdidas Tuberías* |
15% Pérdidas Tuberías* |
Utilizando Diagrama de Moody* |
Utilizando Ecuación 7 |
|||
Trabajo 1 |
356.76 |
53.51 |
0.15 |
51.25 |
0.14 |
87.55 |
25% |
Trabajo 2 |
460.41 |
69.06 |
0.15 |
158.36 |
0.34 |
155.56 |
34% |
Trabajo 3 |
467.36 |
70.10 |
0.15 |
142.55 |
0.31 |
140.21 |
30% |
Trabajo 4 |
287.64 |
43.15 |
0.15 |
93.85 |
0.33 |
89.17 |
31% |
Trabajo 5 |
292.05 |
43.81 |
0.15 |
100.60 |
0.34 |
96.38 |
33% |
Trabajo 6 |
297.25 |
44.59 |
0.15 |
88.20 |
0.30 |
83.23 |
28% |
Trabajo 7 |
288.50 |
43.28 |
0.15 |
95.89 |
0.33 |
92.32 |
32% |
Trabajo 8 |
67.34 |
10.01 |
0.15 |
24.20 |
0.36 |
20.20 |
30% |
Trabajo 9 |
69.05 |
10.36 |
0.15 |
25.40 |
0.37 |
20.72 |
30% |
Trabajo 10 |
66.85 |
10.03 |
0.15 |
22.38 |
0.33 |
20.06 |
30% |
** Estos valores no tienen unidades, ya que representa una relación entre fuerzas.
4. Conclusiones
En este artículo se presenta el desarrollo de una ecuación que permite estimar el factor de fricción (fT) para diferentes piezas especiales y accesorios. Esta herramienta permite estimar de una forma analítica valores de las pérdidas por fricción en un análisis de un sistema de tuberías y accesorios para una edificación cualquiera. Para desarrollar dicha ecuación se utilizaron datos obtenidos del Diagrama de Moody.
Iniciando en el número de Reynolds que identifica el flujo turbulento (4000), se hizo el análisis con una variación de los números marcados en el diagrama de Moody para el numero de Reynolds. Es decir, para cada número de Reynolds tuvimos un valor del factor de fricción para los diferentes accesorios. Ya con esto se usaron los programas de EXCEL y de MATLAB para analizar la curva que mejor se ajusta a los datos. Se propusieron cuatro curvas o modelos matemáticos diferentes, siendo la siguiente formula, la que obtuvo la mayor aproximación de fracciones racionales (RAT):
La ecuación fue validada en dos estudios de casos independientes y como parte del programa de estudios de los estudiantes de Hidráulica II del Instituto Tecnológico de Santo Domingo. El uso de la ecuación desarrollada permite no solo el dejar de estimar los valores de pérdidas en los accesorios, sino que puede ser utilizado en cualquier cálculo de pérdidas por fricción en sistemas sanitarios de agua impulsadas a presión, con diferencias muy mínimas con los métodos utilizados hasta ahora, y en un tiempo mucho menor. Un segundo uso que puede tener la ecuación presentada es la posibilidad de integrar dicha fórmula en los diferentes programas de la Ingeniería Hidráulica.
Referencias
Agudelo Martínez, M. F., & Arango Ramírez, A. (2018). Diseño de material didáctico para las prácticas de laboratorio en mecánica de fluidos e hidráulica de la Universidad EIA. Universidad EIA.
Anaya-Durand, A. I., Cauich-Segovia, G. I., Funabazama-Bárcenas, O., & Gracia-Medrano-Bravo, V. A. (2013). Evaluación de ecuaciones de factor de fricción explícito para tuberías. Educación Química.
Batista de Lima, I., Gabriel Ferreira, P. J., Cearamicoli Vivaldini, T., Daliberto Frugoli, A., & Américo Frugoli, P. (2015). Theoretical and Practical Integrated: Engaging Engineering Students in Fluid Mechanics Class. Proceedings of the 2015 International Conference on Operations Excellence and Service Engineering.
Brown, G. O. (2002). The History of the Darcy-Weisbach Equation for Pipe Flow Resistance. Environmental and Water Resources History, 34–43. https://doi.org/10.1061/40650(2003)4
Camaraza Medina, Y. (2011). Nuevo Modelo para la Determinación del Factor de Fricción en el régimen de flujo turbulento. Revista Arquitectura e Ingeniería.
Diehl, E. (2023). Simulation Project to Promote Learner Autonomy in an Introductory Fluid Mechanics Course. 2023 ASEE Annual Conference & Exposition Proceedings. https://doi.org/10.18260/1-2--44220
Fernández Bolaños, D. A., & Perez Cristancho, B. (2010). Diseño, construcción y calibración de un modelo físico para el estudio de pérdidas de energía.
Florescu, I., Florescu, D., & Nedelcu, D. I. (2012). Study about the fluid losses in the branching pipes. Proceedings in Manufacturing Systems.
Gunadi, G. G. R., Siswantara, A. I., & Budiarso, B. (2018). Turbulence Models Application in Air Flow of Crossflow Turbine. International Journal of Technology, 9(7), 1490. https://doi.org/10.14716/ijtech.v9i7.2636
Huilier, D. G. F. (2019). Forty Years’ Experience in Teaching Fluid Mechanics at Strasbourg University. Fluids, 4(4), 199. https://doi.org/10.3390/fluids4040199
Iturbide, F., Antonio García, A., Jesús, Á., Jasso, M., Santiago-Alvarado, A., & Ramírez, A. (2017, August 29). Diseño y construcción de un equipo para visualizar el comportamiento de los fluidos en regímenes laminar y turbulento. Memorias del XXIII Congreso Internacional Anual de la SOMIM.
Levenspiel, O. (2007). Chemical Reaction Engineering. Wiley.
Mandavgane, S. (2020). Fun with fluid: An innovative assignment in fluid mechanics. Education for Chemical Engineers, 30, 40–48. https://doi.org/https://doi.org/10.1016/j.ece.2019.11.001
Melendez, M. A. (2016). Introducción a la Mecánica de Fluidos. Instituto Tecnológico de Santo Domingo.
Miller, R. W. (1996). Flow Measurement Engineering Handbook (3rd ed.). McGraw Hill.
Moody, L. F. (1944). Friction Factors for Pipe Flow, Transactions of the American Society of Mechanical Engineers, 66.
Plascencia, G., Díaz–Damacillo, L., & Robles-Agudo, M. (2020). On the estimation of the friction factor: a review of recent approaches. SN Applied Sciences, 2(2), 163. https://doi.org/10.1007/s42452-020-1938-6
Roberson, J. A., & Crowe, C. T. (2000). Engineering Fluid Mechanics. Wiley.
Shah, R. K., & London, A. L. (1978). Laminar Flow Forced Convection in Ducts: A Source Book for Compact Heat Exchanger Analytical Data. Academic Press.
Singh, N., Jadhav, R. S., & Agrawal, A. (2017). Derivation of stable Burnett equations for rarefied gas flows. Physical Review E., 96(1). https://doi.org/10.1103/physreve.96.013106
_______________________________
a Área de Ingeniería, Instituto Tecnológico de Santo Domingo. ORCID: 0000-0003-2218-3445. Correo-e: martin.melendez@intec.edu.do
b Área de Ciencias Básicas, Instituto Tecnológico de Santo Domingo. ORCID: 0000-0003-4594-071X. Correo-e: javier.garcia@intec.edu.do
c Área de Ingeniería, Instituto Tecnológico de Santo Domingo. ORCID: 0000-0002-4255-3450. Correo-e: deyslen.mariano@intec.edu.do
d Área de Ingeniería, Instituto Tecnológico de Santo Domingo. ORCID: 0000-0002-4715-3499. Correo-e: miguel.aybar@intec.edu.do
