Ciencia, Ingenierías y Aplicaciones, Vol. 6, No. 2, julio-diciembre, 2023 ISSN (impreso): 2636-218X • ISSN (en línea): 2636-2171 • Sitio web: https://revistas.intec.edu.do/

SELECCIÓN DEL MODELO ÓPTIMO DE LA RELACIÓN DE DESEMPEÑO DE UNA PLANTA SOLAR FOTOVOLTAICA. UN ENFOQUE MULTICRITERIO BASADO EN ALGORITMOS DE APRENDIZAJE AUTOMÁTICO

Selection of the optimal model for predicting the performance ratio of a photovoltaic solar plant. A multi-criteria approach based on machine learning algorithms

DOI: https://doi.org/10.22206/cyap.2023.v6i2.2935

CÉSAR A. YAJURE RAMÍREZ

Universidad Central de Venezuela, Caracas, Venezuela. ORCID: 0000-0002-3813-7606, Correo-e: cyajure@gmail.com

Recibido: 04/09/2023 • Aprobado: 3/11/2023

Cómo citar: Yajure Ramírez, C. A. (2023). Selección del modelo óptimo de predicción de la relación de desempeño de una planta solar fotovoltaica. Un enfoque multicriterio basado en algoritmos de aprendizaje automático. Ciencia, Ingenierías y Aplicaciones, 6(2), 7–29. https://doi.org/10.22206/cyap.2023.v6i2.2935

1. Introducción

El análisis de desempeño de las plantas solares fotovoltaicas incluye la revisión periódica de un conjunto de indicadores diseñados para tal fin, y que se encuentran en los estándares de la Comisión Electrotécnica Internacional (IEC por sus siglas en inglés). Entre los indicadores se tiene a la relación de desempeño (PR por sus siglas en inglés) de la planta, el cual se define como el cociente entre el rendimiento final del sistema y el rendimiento de referencia, e indica el efecto total de las pérdidas sobre la salida del sistema debido tanto a la temperatura del arreglo como a la ineficiencia o falla de los componentes del sistema (International Electrotechnical Commission, 2017, p. 38). En el cálculo de este indicador se debe considerar una corrección por temperatura, para compensar la diferencia entre la temperatura real de los paneles solares y la temperatura de 25°C considerada en las condiciones estándar de prueba (STC por sus siglas en inglés).

Es de interés entonces que el PR sea lo más cercano posible al 100%, lo cual indicaría que las pérdidas son mínimas. En ese sentido, Khalid et al. (2016) plantean que, de acuerdo con la Unión Europea, un PR mayor o igual al 80% es un indicador de buen desempeño del sistema, y un valor por debajo del 75% es indicativo de algún problema en la planta. Por consiguiente, sería un gran aporte contar con una herramienta que nos permita pronosticar si el PR de una planta solar fotovoltaica estará por encima o por debajo del 80%. Desde el punto de vista de la ciencia de datos, este sería un ejemplo de clasificación binaria para el que se cuenta con una variedad de algoritmos de aprendizaje automático, y a priori no se sabría con certeza cuál es el algoritmo que proporciona resultados óptimos y sirve como el modelo más eficaz del sistema.

Por lo anterior, el objetivo de esta investigación es presentar una metodología multicriterio para seleccionar el mejor modelo de clasificación para la relación de desempeño de una planta solar fotovoltaica. Esta metodología se ilustra utilizando los datos de una planta solar fotovoltaica comercial ubicada en la zona central de Chile. Para el estudio se considera la técnica para el orden de preferencia por similitud con la solución ideal (TOPSIS por sus siglas en inglés) como herramienta multicriterio de análisis, y los algoritmos de aprendizaje automático: K vecinos más cercanos (K-NN por sus siglas en inglés), bosques aleatorios, clasificador de soporte vectorial (SVC por sus siglas en inglés), y regresión logística.

Se hizo una revisión de las investigaciones ya realizadas relacionadas con el tema de esta investigación, y no se encontró alguna que haya aplicado las técnicas formales multicriterio para seleccionar modelos de clasificación. Por ejemplo, Vujović (2021) evaluó cuatro algoritmos de clasificación utilizando el software Weka, y considerando hasta dieciséis métricas de evaluación, jerarquizando los modelos por cada una de esas métricas. Utilizó los datos de pacientes egipcios con el virus de hepatitis C, generando cuatro clases, dependiendo del nivel de gravedad de la enfermedad. Obtuvo que el desempeño de los modelos no fue el esperado, y sugiere realizar un procesamiento adicional a los datos. Varoquaux & Colliot (2023) presentan una metodología para evaluar y seleccionar modelos de aprendizaje automático, tanto de clasificación como de regresión. Describen las métricas utilizadas para evaluar los modelos de clasificación binaria y multiclase, recordando que la curva ROC se diseña considerando varios puntos de corte, no sólo el de probabilidad igual a 0,5, y que además se resume en un valor único, el AUC. Una de las estrategias que proponen es el uso de distintas técnicas validación cruzada: k-fold, hold-out repetido, entre otras, así como la repetición de experimentos para obtener intervalos de confianza para las métricas de evaluación consideradas. (Westphal & Brannath (2019) investigan las propiedades de las estrategias de evaluación innovadoras en las que el modelo final es seleccionado con base en su desempeño empírico con los datos de prueba, y emplean un test paramétrico múltiple para estimar el desempeño. Utilizan los algoritmos XGBoost, SVM, CART, y EN, para clasificación, a través del software R. Obtienen que el algoritmo XGBoost es el que tiene mayores probabilidades de aprender el mejor modelo de predicción, para las distintas tareas de clasificación, y que con la estrategia propuesta mejoran el error de clasificación en un 10%. Kirasich, Smith, & Sadler (2018) evalúan el desempeño de modelos de clasificación generados a través de los algoritmos de bosques aleatorios y regresión logística utilizando conjuntos de datos con distintas estructuras subyacentes. Desarrollan una herramienta de evaluación de modelo capaz de simular modelos clasificadores, y con métricas de desempeño tales como: tasa de positivos verdaderos, tasa de positivos falsos, y exactitud. Encuentran que cuando se incrementa la varianza en las variables explicativas, la regresión logística desarrolla consistentemente una exactitud más alta comparada con los modelos de bosques aleatorios. Sin embargo, la tasa de positivos verdaderos para bosques aleatorios es más alta que para el modelo de regresión logística cuando se incrementan las variables ruidosas en el experimento. Dhabarde (2019) revisa las diferentes técnicas utilizadas para selección de algoritmos de aprendizaje automático, y para la evaluación y selección de modelos de machine learning. Considera en detalle el método de retención para la evaluación de los modelos, diferentes variantes de remuestreo para estimar la incertidumbre de los valores de desempeño, técnicas de validación cruzada, compensación error-varianza, entre otras. Yajure-Ramírez (2023) presenta una metodología multicriterio para la selección de modelos de regresión utilizando la técnica TOPSIS. Considera los algoritmos de regresión lineal múltiple, red neuronal artificial, regresor de árbol de decisión, regresor K-NN, y regresor de soporte vectorial. Las métricas de evaluación consideradas fueron: R², RMSE, MAE, y MAPE. Utilizando datos de consumo de energía eléctrica residencial, encontró que el modelo de regresión lineal múltiple obtuvo el mayor valor del indicador de desempeño con 0,826. Finalmente, Puleko et al. (2022) proponen una metodología para evaluar la calidad de los algoritmos de clasificación por medio de un indicador escalar obtenido por convolución de otros indicadores. Para ilustrar la metodología utilizan el clásico conjunto de datos “iris”, así como otro conjunto de datos práctico, y los algoritmos: regresión logística, análisis discriminante lineal, K vecinos más cercanos, árboles de decisión, clasificador Naive-Bayes, y máquinas de soporte vectorial. El indicador escalar utilizado es el esquema de compromiso no lineal NSC, y mientras mayor su valor, mejor. Como resultados obtuvieron que para el conjunto de datos “iris”, el modelo de máquina de soporte vectorial tuvo el mejor desempeño con un NSC de 10.096 y 10.083 para las clases versicolor y virginica, respectivamente. Para el conjunto real, el mejor desempeño lo tuvo el modelo de árboles de decisión con un NSC de 12,46.

El resto del artículo se distribuye de la siguiente manera. En la sección 2 se presenta la metodología planteada y los datos utilizados para ilustrarla. Luego, en la sección 3 se presentan y analizan los resultados obtenidos. Posteriormente, se presentan las conclusiones que se derivan de esta investigación. Por último, se presentan las referencias bibliográficas.

2. Materiales y métodos

La metodología empleada se basa en utilizar las etapas de un proceso de ciencia de datos y agregar una etapa de toma de decisiones multicriterio. Tal como lo plantean (Cielen, Meysman, & Ali, 2016, pág. 23), el proceso de ciencia de datos consta de seis pasos o etapas, cuatro de las cuales se muestran en el esquema de la metodología empleada de la Figura 1.

La primera etapa consiste en definir el o los objetivos, puesto que se requieren para el desarrollo de las siguientes etapas. Enmarcado dentro del proceso de ciencia de datos, el objetivo sería predecir la clase del PR de una planta solar fotovoltaica, utilizando modelos de clasificación. Luego, se deben obtener los datos necesarios a utilizar para alcanzar el objetivo, los que podrían provenir tanto de fuentes internas como externas, y normalmente serán datos “crudos” que requerirán cierto procesamiento. Esto último corresponde a la tercera etapa, en la cual se aplican distintas técnicas, tales como: manejo e imputación de datos faltantes, manejo de datos duplicados, unir datos de distintas fuentes, combinar datos para crear nuevos atributos, verificar formato de los datos, entre otras (McKinney, 2018). En la siguiente etapa, se seleccionan los modelos de clasificación a utilizar, y se aplican para obtener los modelos que permitan predecir la clase del PR. Al finalizar esta etapa, se tienen disponibles los valores de las métricas de evaluación de los modelos de clasificación utilizados, los cuales son insumos para la etapa de toma de decisiones multicriterio. Seguidamente, se selecciona y aplica la técnica de toma de decisión multicriterio, teniendo a los distintos modelos como las alternativas, y a las métricas de evaluación como los criterios de decisión. En esta sección se presentan las etapas de obtención y preprocesamiento de los datos, y en la siguiente sección el resto de las etapas de la metodología.

2.1 Evaluación de modelos de clasificación

Los algoritmos de clasificación caen dentro del aprendizaje automático supervisado, y permiten obtener modelos que pudieran ser de dos tipos, binario y multiclase. El primero de ellos corresponde a casos en los que sólo se consideran dos clases para la clasificación, mientras que el segundo de ellos considera más de dos clases. Para medir el desempeño de los modelos de clasificación binaria, hay distintas métricas, tanto analíticas como gráficas, que por lo general se obtienen a partir de los valores de las celdas de la matriz de confusión, y que requieren que de manera genérica se defina una clase positiva (1) y una clase negativa (0). Esta matriz de confusión se consigue a partir de las predicciones del set de prueba, y es una matriz cuadrada con tantas filas como clases existan, por lo que se está hablando de una matriz de 2x2. De acuerdo con Raschka & Mirjalili (2017, p. 206) “La matriz de confusión es simplemente una matriz cuadrada que reporta el conteo de positivos verdaderos, negativos verdaderos, positivos falsos, y negativos falsos, de las predicciones de un clasificador”.

Entonces, la matriz tiene cuatros celdas, el valor de la celda (1,1) corresponde al número de registros de la clase positiva que el modelo considerado predijo correctamente como pertenecientes a la clase positiva, se les llama positivos verdaderos (TP por sus siglas en inglés). Asimismo, el valor de la celda (0,0) corresponde al número de registros de la clase negativa que el modelo considerado predijo correctamente como negativos, se les llama negativos verdaderos (TN por sus siglas en inglés). La celda (0,1) tiene el número de registros con clase real negativa, pero que el modelo predijo que eran de la clase positiva, y se le llaman positivos falsos (FP por sus siglas en inglés). Finalmente, en la celda (1,0) está el número de registros con clase real positiva, pero que el modelo los predijo como de la clase negativa, y a estos registros se les llama negativos falsos (FN por sus siglas en inglés).

2.1.1 Métricas para evaluación de desempeño de modelos de clasificación

A partir de los valores de las celdas de la matriz de confusión, se calculan una serie de métricas para evaluar el desempeño de los modelos de clasificación: Exactitud, Precisión, Recall o tasa de positivos verdaderos (TPR por sus siglas en inglés), F1-Score, y tasa de positivos falsos (FPR por sus siglas en inglés). Según lo que indica Lee (2019, p. 170), la Exactitud “es definida como la suma de todas las predicciones correctas dividida entre la suma de todas las predicciones”, se calcula aplicando la Ecuación (1). La Precisión “está relacionada con el número de predicciones positivas correcta”, y se calcula con la Ecuación (2). El Recall “está relacionada con el número de eventos positivos predichos correctamente”, se calcula con la Ecuación (3). El F1-Score “es conocido como la media armónica entre la precisión y el recall”, se calcula con la Ecuación (4). La tasa de positivos falsos FPR “corresponde a la proporción de registros negativos que son erróneamente considerados como positivos, con respecto a todos los registros negativos”, se calcula con la Ecuación (5).

$$Exactitud=\frac{TP+TN}{TP+TN+FP+FN}\mathrm{ (1)}$$

$$Precisión=\frac{TP}{TP+FP}\mathrm{ (2)}$$

$$recall=\frac{TP}{TP+FN}\mathrm{ (3)}$$

$$F1-Score=\frac{2·(precisión·recall)}{precisión+recall}\mathrm{ (4)}$$

$$FPR=\frac{FP}{FP+TN}\mathrm{ (5)}$$

2.1.2 Curva ROC

Otra herramienta que se puede utilizar para seleccionar el mejor modelo de clasificación es la curva ROC (Receiver Operating Characteristic). De acuerdo con Haroon (2017, p. 183), esta curva “presenta la fracción de positivos verdaderos del total de positivos (TPR) versus la fracción de positivos falsos del total de negativos (FPR)”. Es decir, la curva se crea graficando TPR versus FPR a distintos puntos de corte (thresholds). Asociado a esta curva está el indicador AUC (Area Under Curve), cuyo valor varía entre 0 y 1. Mientras más cercano a 1 es el valor de AUC, mayor área y mejor desempeño presenta el modelo de clasificación.

2.2 Toma de decisiones multicriterio

La toma de decisiones multicriterio (Multicriteria Decision Making, MCDM) está relacionada con los problemas de decisión en los que se debe seleccionar una alternativa de un conjunto de alternativas, considerando más de un criterio de decisión. La MCDM se divide en toma de decisiones multiobjetivo (Multiobjective Decision Making, MODM), y toma de decisiones multiatributo (Multiattribute Decision Making, MADM). De acuerdo con Eltarabishi et al. (2020, p. 2655) “La MADM trata con problemas de decisión que tienen un objetivo implícito y un espacio de decisión discreto (número finito de alternativas y atributos). Por otra parte, la MODM problemas que tienen objetivos explícitos y un espacio de decisión continuo (número infinito de alternativas y atributos)”.

Una manera de representar un problema de decisión multiatributo es a través de una matriz de decisión (m×n), en la que su elemento a_ij indica el desempeño de la alternativa A_i cuando es evaluada en términos del criterio de decisión C_j, para i = 1, 2 ,3 , … , m, y j = 1, 2, 3, … , n (Triantaphyllou et al., 1998). Un punto para destacar es que los criterios de decisión tienen un peso de importancia relativa w_j, que usualmente son definidos por el analista y/o el tomador de decisión. Entonces, dado un conjunto de alternativas y un conjunto de criterios de decisión, con sus respectivos pesos de importancia relativa, la meta es encontrar la mejor alternativa con el grado más alto de “deseabilidad” con respecto a los criterios de decisión.

Ishizaka & Nemery (2013, pp. 3-4) utilizan la clasificación de problemas de decisión planteada por Roy en 1981, quien identificó cuatro tipos principales de decisión: problemas de selección, problemas de clasificación, problemas de jerarquización, y problemas de descripción. En esta investigación nos interesa el problema de selección, en el que “La meta es seleccionar la mejor alternativa o reducir el grupo de alternativas a un subconjunto de equivalentes o incomparables ‘buenas’ alternativas”. Para abordar los problemas de decisión existe una variedad de técnicas multicriterio, que pueden discriminarse dependiendo del tipo de problema de decisión presente. Por ejemplo, para problemas de selección, se pudieran aplicar las técnicas: AHP, ANP, Promethee, Electré, TOPSIS, Programación meta, entre otras.

2.2.1 Técnica multicriterio TOPSIS

En esta investigación se utiliza la técnica TOPSIS ya que como lo plantean Velasquez & Hester (2013, p. 64), esta técnica “posee un procedimiento sencillo, es fácil de usar y programar, y el número de pasos sigue siendo el mismo independientemente del número de criterios”. Asimismo, esta técnica se basa en seleccionar la mejor alternativa midiendo la distancia geométrica más corta a la solución positiva ideal, y la distancia geométrica más larga a la solución negativa ideal (Sahoo et al., 2022).

La técnica TOPSIS está compuesta por seis pasos, el primero de los cuales consiste en obtener la matriz de decisión, compuesta por m filas (alternativas) y n columnas (criterios de decisión). Cada celda de la matriz corresponderá al desempeño de cada alternativa con respecto a cada criterio, es decir, el desempeño de cada modelo de clasificación con respecto a cada una de las métricas de evaluación. Luego, el desempeño de las distintas alternativas debe ser normalizado para poder comparar valores de distintas unidades, y así se obtiene la matriz de decisión normalizada utilizando la Ecuación (6). Posteriormente, cada celda se pondera con el peso de importancia relativa respectivo aplicando la Ecuación (7), para generar la matriz de decisión normalizada ponderada. A continuación, se calculan la solución ideal positiva A^* y la solución ideal negativa A^–, utilizando las Ecuaciones (8) y (9), respectivamente. La distancia de cada alternativa con respecto a las soluciones ideales se obtiene al usar las Ecuaciones (10) y (11). A continuación, se aplica la Ecuación (12) para obtener la cercanía relativa de cada alternativa con la solución ideal $C_i^{*}$ (Papathanasiou & Ploskas, 2018).

El valor de $C_i^{*}$ varía entre 0 y 1, y mientras más cercano a 1, la alternativa respectiva tiene mejor desempeño. Finalmente, las alternativas se jerarquizan de acuerdo con este indicador, y la que ocupe el primer lugar será la seleccionada.

$$r_{ij}=\frac{a_{ij}}{\sqrt{\sum _{i=1}^m{a}_{ij}^2}}\mathrm{ (6)}$$

$$v_{ij}=w_j·r_{ij}\mathrm{ (7)}$$

$$A^{*}=\{v_1^{*},v_2^{*},\dots ,v_n^{*}\}=\left\{\underset{j}{max}{v}_{ij}\right\}\mathrm{ (8)}$$

$$A^{-}=\{v_1^{-},v_2^{-},\dots ,v_n^{-}\}=\left\{\underset{j}{min}{v}_{ij}\right\}\mathrm{ (9)}$$

$$D_i^{*}=\sqrt{\sum _{j=1}^n{(v_{ij}-v_j^{*})}^2}\mathrm{ (10)}$$

$$D_i^{-}=\sqrt{\sum _{j=1}^n{(v_{ij}-v_j^{-})}^2}\mathrm{ (11)}$$

$$C_i^{*}=\frac{D_i^{-}}{D_i^{-}+D_i^{*}}\mathrm{ (12)}$$

2.3 Obtención de los datos

Los datos conciernen a las mediciones de las variables eléctricas de una planta solar fotovoltaica, ubicada en la zona central de Chile, y las correspondientes mediciones de las variables climáticas. Todas las mediciones se realizaron a intervalos de quince minutos, y fueron realizadas durante el período que va desde enero del año 2021 hasta la primera quincena del mes de enero del año 2023. Esta planta de 109,49 MW nominales de potencia AC, incluye 397.565 paneles solares de variadas marcas comerciales y capacidades. En una primera etapa fueron instalados 101 inversores marca INGETEAM, 53 unidades transformadoras elevadoras y un transformador principal de relación nominal 22/220 kV y 130 MVA de potencia nominal, estando estas instalaciones ubicadas a 800 msnm. Posteriormente, en una ampliación se instalaron adicionalmente 35 inversores marca HUAWEI SUN2000TL de 185 kW cada uno (Estudios energéticos consultores, 2021).

El conjunto de datos incluye la sumatoria de la energía eléctrica AC a la salida de los inversores (“Inv_kWh”), la energía eléctrica AC que entrega la planta (“Plant_kWh”), y las pérdidas de energía en la planta (“Energy Losses”), en kilovatios-hora (kWh). De igual forma, el promedio de la temperatura ambiente (“Tamb_Avg”) y el promedio de la temperatura de los paneles solares (“Tbom_Avg”), ambos en grados Celsius (°C). La irradiancia solar que llega a los paneles solares (“POA_Avg”) y la irradiancia global horizontal (“GHI”), ambas en vatios por metro cuadrado (W/m2). Además, la suma de la potencia AC entregada por los inversores (“SumInv_kW”), y los valores de potencia AC entregados por la planta (“Plant_kW”), ambos en kilovatios (kW). Asimismo, la fecha de la medición, así como el año, el mes, el día, y la hora de la medición. En total son 71.773 filas y 14 columnas correspondientes a las variables mencionadas previamente.

2.4 Preprocesamiento de los datos

En principio, se revisó la posible existencia de datos faltantes, de los cuales se encontraron doce en las columnas de la temperatura ambiente y la temperatura de los módulos, los cuales se imputaron con los valores promedios de los últimos cuatro valores diferentes de cero. De igual manera, se chequeó la posible existencia de datos duplicados, detectándose 288 filas duplicadas correspondientes a las mediciones de los días 28, 29, y 30 de noviembre del 2022, las cuales fueron eliminadas, para llegar a un total de 71.485 filas.

A continuación, se utilizó la columna de la irradiancia solar, para crear la columna de la irradiación solar (“irradiation_Wh/m2”), la cuál de acuerdo con SolarPower Europe (2021, p. 72) “se calcula como la suma de las irradiancias en un período de tiempo. Es comúnmente expresado como kilovatio-hora por metro cuadrado (kWh/m2)”. Esta variable recién creada se utiliza para calcular el rendimiento de referencia definido como la relación entre la irradiación solar para un período de tiempo y la irradiancia solar a las condiciones estándar de prueba (International Electrotechnical Commission, 2017). Asimismo, se toma la columna de la energía eléctrica entregada por la planta para calcular el rendimiento específico, el cual se define como la relación entre la energía eléctrica producida por la planta en un período de tiempo y la potencia nominal pico DC de la planta (International Electrotechnical Commission, 2017). Luego, utilizando los dos rendimientos mencionados previamente, se genera la columna del PR. De igual forma, al usar la columna de la energía eléctrica se genera la columna del factor de capacidad de la planta CF, definido como la relación entre la energía eléctrica entregada por la planta y la energía que entregaría la planta a su máxima capacidad (International Electrotechnical Commission, 2016). Luego, se toma la columna de la energía para generar la columna de la eficiencia AC de la planta (Eff_AC).

Posteriormente, los datos 15-minutales fueron agrupados para generar un set de datos diarios, el cual fue utilizado en las etapas de análisis exploratorio y modelación de los datos.

3. Análisis y discusión de resultados

En esta sección se aplica la metodología planteada utilizando los algoritmos de clasificación de K vecinos más cercanos (K-NN por sus siglas en inglés), bosques aleatorios, máquinas de soporte vectorial (SVC por sus siglas en inglés), y regresión logística, como las alternativas del problema de decisión. En cuanto a los criterios de decisión, se consideran: exactitud, precisión, F1-Score, recall, y AUC. Como variable objetivo de los modelos de clasificación se tiene a la relación de desempeño PR, para lo cual se definieron dos clases: mayor o igual a 80%, y menor a 80%.

Para todos los algoritmos de clasificación aplicados se consideró el set de datos diarios, el cual consta de 745 registros. Este set se dividió en dos partes de manera aleatoria: el 70% de los datos (521 registros) se utiliza para el entrenamiento del modelo, y el 30% restante para la prueba de ese modelo.

3.1 Uso de algoritmo de K vecinos más cercanos

K-NN es un algoritmo de aprendizaje automático de tipo supervisado, que se puede utilizar para desarrollar modelos tanto de regresión como de clasificación, y según Fenner (2020, p. 65), esta técnica de aprendizaje es del tipo no paramétrica. Sin embargo, dado que el principio básico consiste en considerar los elementos que son similares entre sí (vecinos más cercanos), se requiere conocer de antemano el número de vecinos K a tomar en cuenta. Se han propuesto varias metodologías para obtener el valor de K, por ejemplo, Maleki et al. (2017) proponen utilizar las técnicas de validación cruzada. En esta investigación se obtiene el valor óptimo de K graficando el número de vecinos más cercanos versus la exactitud, y se escoge aquel valor de K que maximiza esta métrica.

El valor óptimo de K resultó ser igual a 5. A partir del set de pruebas se realizan predicciones utilizando el modelo entrenado, y se calculan las métricas de evaluación del modelo, los cuales se presentan a continuación: Exactitud = 0,9286, Precisión = 0,8909, F1-Score = 0,9069, Recall = 0,9277.

3.2 Uso de algoritmo de bosques aleatorios

El algoritmo de bosques aleatorios pertenece a la familia de aprendizaje automático supervisado, y también cae dentro de la definición de los métodos de aprendizaje de conjunto (ensemble methods). Consiste en crear múltiples árboles de decisión a partir de un mismo conjunto de datos, utilizando la técnica de remuestreo con reemplazo con el fin de reducir la varianza. Russano & Ferreira Avelino (2020, p. 206) plantean que una vez que se tienen los modelos de clasificación, se realizan predicciones con cada uno de ellos y se combinan los resultados aplicando una de dos posibles vías: tomar el voto mayoritario, es decir, el resultado que más se repite para el caso de problemas de clasificación, o tomar el promedio de los resultados en caso de problemas de regresión.

Para la definición del bosque aleatorio, se toman sus parámetros por defecto, es decir, número de árboles de decisión igual a cien, “gini” como criterio para medir la calidad del bosque, entre otros. De nuevo, con el conjunto de prueba se realizan predicciones utilizando el modelo entrenado, resultando que las variables que más aportan a la calidad del bosque fueron la temperatura de los paneles solares y la irradiancia solar. En cuanto a las métricas de evaluación del modelo, los resultados fueron: Exactitud = 0,9554, Precisión = 0,9378, F1-Score = 0,9425, Recall = 0,9474.

3.3 Uso de máquina de soporte vectorial

Las máquinas de soporte vectorial se crearon inicialmente para tratar problemas de clasificación, y posteriormente se adaptaron para que pudieran utilizarse en problemas de regresión utilizando el mismo principio de funcionamiento. El algoritmo de soporte vectorial utiliza el concepto de kernel para convertir los datos dados en una dimensión superior, para así conseguir los hiperplanos. Los puntos ubicados a cada lado del hiperplano y que estén más cercanos a él se conocen como vectores de soporte. Hay cuatro tipos principales de kernel, a saber, lineal, polinómico, sigmoidea y función de base radial (Muthukrishnan & Jamila. S, 2020).

Para nuestro caso de estudio se utiliza el clasificador de soporte vectorial, considerando sus parámetros por defecto, lo cual incluye un kernel de función de base radial. El modelo entrenado se utiliza para realizar predicciones utilizando el conjunto de prueba, resultando que las métricas de evaluación del modelo fueron: Exactitud = 0,8527, Precisión = 0,8226, F1-Score = 0,8091, Recall = 0,7986.

3.4 Uso de regresión logística

Este algoritmo es de aprendizaje automático supervisado, y a través de su aplicación se pueden obtener modelos para clasificación binaria. De acuerdo con Kirasich et al. (2018, p. 8), esta técnica “ Es uno de los modelos estadísticos lineales más utilizados para análisis discriminante”. Luego se realizar una regresión lineal, la técnica transforma la salida de esta regresión a través de una función logística (de allí su nombre), que por lo general es la función sigmoide. Está última función asigna una probabilidad condicional para cada clase.

Para la aplicación del algoritmo se tomaron todos los parámetros por defecto, lo que incluyó el método de optimización lbfgs. Tal como en los otros algoritmos, el modelo entrenado se utiliza para realizar predicciones utilizando el conjunto de prueba, resultando que las métricas de evaluación del modelo fueron: Exactitud = 0,9777, Precisión = 0,9659, F1-Score = 0,9689, Recall = 0,9720.

3.5 Curvas ROC de cada modelo clasificador

Se obtuvieron las curvas ROC de cada modelo clasificador considerado, y se obtuvo el área bajo cada una de esas curvas para utilizarlo como métrica de evaluación. En la Figura 2 se muestran los resultados obtenidos. Según lo planteado por Rogel-Salazar (2017, pp. 202-203), serán mejores las curvas que más se acerquen a la esquina superior izquierda, es decir, cuando la fracción de positivos falsos sea nula, y la fracción de positivos verdaderos sea máxima. Los modelos en esa esquina tendrían un AUC del 100%. Asimismo, indica que la línea punteada representaría un clasificador que hace sus predicciones al azar con un área bajo la curva del 50%. Por debajo de esta línea punteada estarían los clasificadores con AUC menores al 50%.

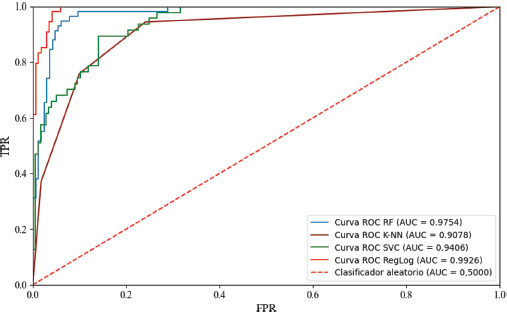
Entonces, de la Figura 2 se puede ver que, bajo este criterio, el mejor modelo considerado sería el de la regresión logística (RegLog) seguido del modelo asociado a bosques aleatorios (RF), y el peor modelo sería el desarrollado con el algoritmo K-NN.

3.6 Selección multicriterio del mejor modelo

3.6.1 Pesos de importancia de los criterios

Antes de aplicar la técnica TOPSIS, primero se deben calcular los pesos de importancia relativa de los criterios de decisión utilizando la técnica de las comparaciones pareadas propuesta por Saaty, quien definió una escala de números que indican cuantas veces es más importante un elemento con respecto a otro elemento, según el criterio o propiedad usado para compararlos. La intensidad de importancia va desde “1” hasta “9”, siendo “1” cuando los elementos tienen igual importancia y “9” cuando el elemento es extremadamente más importante con respecto al otro elemento (Saaty, 2008). En la Tabla 1 se presenta la matriz de comparaciones pareadas para los criterios de decisión: Exactitud, Precisión, F1-Score, Recall, y AUC.

A partir de la matriz de comparaciones pareadas se obtienen los pesos de importancia relativa de los criterios, aplicando un procedimiento práctico que Moreno Jiménez (2002, p. 16) llama “el método de las potencias”, que consiste en elevar la matriz de comparaciones pareadas a una potencia suficientemente grande, sumando por filas y normalizando estos valores mediante la división de la suma de cada fila por la suma total, deteniendo el proceso cuando la diferencia entre dos potencias consecutivas sea mínima. En la Tabla 2 se presentan los resultados obtenidos, de la que se puede notar que el AUC es el criterio con mayor importancia relativa.

Se verificó la consistencia de estos pesos de importancia relativa de acuerdo con el procedimiento de la razón de consistencia RC, resultando una RC de solo el 0,2% de un máximo del 10% requerido para aceptar los resultados desde un punto de vista práctico (Moreno Jiménez, 2002, p. 17).

3.6.2 Selección óptima del modelo de clasificación

Los resultados de las métricas de evaluación para cada modelo conforman la matriz de decisión de nuestro problema de decisión, y esta se presenta en la Tabla 3. Dado que todos los valores corresponden a cifras entre 0 y 1, no será necesario normalizar la matriz.

El siguiente paso en la aplicación de la técnica TOPSIS, consiste en calcular la matriz de decisión ponderada aplicando la Ecuación (7). Esta matriz se presenta en la Tabla 4.

A partir de la matriz de la Tabla 4, se obtiene la solución ideal positiva A^* tomando el valor máximo de cada uno de los criterios. De igual forma, se obtiene la solución ideal negativa A^- al tomar el valor mínimo de los criterios. Con esta información, se aplican las Ecuaciones (10) y (11) para obtener la distancia de cada alternativa con respecto a las soluciones soluciones ideales, $D_i^{*}$ y $D_i^{-}$. Finalmente, se aplica la Ecuación (12) para obtener la cercanía relativa de cada alternativa con la solución ideal. En la Tabla 5 se presentan los resultados, ya jerarquizados de acuerdo con $C_i^{*}$.

De la Tabla 5 se puede ver que el modelo que se obtuvo con Regresión Logística es el que se considera óptimo de acuerdo con la metodología multicriterio aplicada. Se puede ver que alcanzó el puntaje máximo posible, y eso se debe a que la mejor solución para cada uno de los criterios de decisión correspondió a este modelo. También se puede ver que el peor modelo fue el obtenido con el clasificador de soporte vectorial.

4. Conclusiones

Se desarrolló una metodología multicriterio para seleccionar el mejor modelo de clasificación para la predicción de la clase de la relación de desempeño de una planta solar fotovoltaica. Se utilizó la técnica multicriterio TOPSIS, las alternativas de la metodología fueron los modelos de clasificación, y los criterios de decisión fueron las métricas de evaluación de los modelos de clasificación. El modelo de Regresión Logística resultó ser el óptimo con un puntaje máximo de 1,00 seguido por el modelo de bosques aleatorios con un puntaje de 0,8286.

Con la técnica de comparaciones pareadas propuesta por Saaty, se pudieron obtener los pesos de importancia relativa de los criterios de decisión, con una razón de consistencia de sólo el 0,2%, de un límite máximo del 10%, requerido para aceptar los resultados de esta técnica.

Se generaron modelos de clasificación para las clases de la relación de desempeño de una planta solar fotovoltaica comercial, utilizando los algoritmos K-NN, SVC, Bosques aleatorios, y Regresión logística, con valores por encima del 80% para cada una de las métricas de evaluación: Exactitud, Precisión, F1-Score, y Recall. También se graficaron curvas ROC para cada uno de los modelos, resultando valores AUC por encima del 90% para cada uno de ellos, siendo mayor el valor para el modelo de Regresión logística con 99,26%.

Se recomienda continuar la investigación incorporando nuevos modelos de clasificación, otra técnica de análisis multicriterio, y probar nuevamente la metodología planteada.

Referencias

Cielen, D., Meysman, A., & Ali, M. (2016). Introducing Data Science. Shelter Island, NY: Manning Publications Co.

Dhabarde, S. (2019). Approach towards Model Evaluation, Model Selection, and Algorithm Selection in Machine Learning. Pramana Research Journal, 396-408.

Eltarabishi, F., Omar, O., Alsyouf, I., & Bettayeb, M. (2020). Multi-Criteria Decision Making Methods And Their Applications– A Literature Review. Proceedings of the International Conference on Industrial Engineering and Operations Management (págs. 2654-2663). Dubai, UAE: IEOM Society International.

Estudios energéticos consultores. (2021). Informe de determinación de potencia máxima - Parque Solar Fotovoltaico Quilapilún. Santiago de Chile: Grupo Mercados Energéticos Consultores.

Fenner, M. E. (2020). Machine Learning with Python for Everyone. Boston: Pearson Education, Inc.

Haroon, D. (2017). Python Machine Learning Case Studies. Karachi, Pakistan: Apress.

International Electrotechnical Commission. (2016). Photovoltaic system performance – Part 3: Energy evaluation method. (IEC 61724-3).

International Electrotechnical Commission. (2017). Photovoltaic System Performance - Part 1: Monitoring. (IEC 61724-1).

Ishizaka, A., & Nemery, P. (2013). Multi-Criteria Decision Analysis - Methods and Software. West Sussex, United Kingdom: John Wiley & Sons, Ltd.

Khalid, A., Mitra, I., Warmuth, W., & Schacht, V. (2016). Performance ratio – Crucial parameter for grid connected PV plants. Renewable and Sustainable Energy Reviews, 1139-1158. https://doi.org/10.1016/j.rser.2016.07.066.

Kirasich, K., Smith, T., & Sadler, B. (2018). Random Forest vs Logistic Regression: Binary Classification for Heterogeneous Datasets. SMU Data Science Review, https://scholar.smu.edu/datasciencereview/vol1/iss3/9.

Lee, W. M. (2019). Python Machine Learning. Indianapolis: John Wiley & Sons, Inc.

Maleki, M., Manshouri, N., & Kayıkçıoğlu, T. (2017). A Novel Simple Method to Select Optimal k in k-Nearest Neighbor Classifier. International Journal of Computer Science and Information Security, 464-469.

McKinney, W. (2018). Python for Data Analysis. Sebastopol, CA: O’Reilly Media, Inc.

Moreno Jiménez, J. (2002). El proceso analítico jerárquico (AHP). Fundamentos, metodología, y aplicaciones. Revista Electrónica de Comunicaciones y Trabajos de ASEPUMA, 28-77.

Muthukrishnan, R., & Jamila. S, M. (2020). Predictive Modeling Using Support Vector Regression. International Journal of Scientific & Technology Research, 4863-4865.

Papathanasiou, J., & Ploskas, N. (2018). Multiple Criteria Decision Aid - Methods, Examples and Python Implementations. Cham, Switzerland: Springer Nature Switzerland AG.

Puleko, I., Svintsytska, O., Chumakevych, V., Ptashnyk, V., & Polishchuk, Y. (2022). The Scalar Metric of Classification Algorithm Choice in Machine Learning Problems Based on the Scheme of Nonlinear Compromises. 6th International Conference on Computational Linguistics and Intelligent Systems. Gliwice, Poland: CEUR Workshop Proceedings.

Raschka, S., & Mirjalili, V. (2017). Python Machine Learning - Machine Learning and Deep Learning with Python, Scikit-Learn, and TensorFlow. Birmingham: Packt Publishing Ltd.

Rogel-Salazar, J. (2017). Data Science and Analytics with Python. Boca Raton, FL: CRC Press Taylor & Francis Group.

Russano, E., & Ferreira Avelino, E. (2020). Fundamentals of Machine Learning Using Python. Oakville, Canadá: Arcler Press.

Saaty, T. (2008). Decision making with the analytic hierarchy process. International Journal of Services Sciences, 83-98. https://dx.doi.org/10.1504/IJSSCI.2008.017590.

Sahoo, B., Behera, R., & Pattnaik, P. (2022). A Comparative Analysis of Multi-Criteria Decision Making Techniques for Ranking of Attributes for e-Governance in India. International Journal of Advanced Computer Science and Applications, 65-70. https://dx.doi.org/10.14569/IJACSA.2022.0130311.

SolarPower Europe. (2021). Operation & Maintenance - Best Practice Guidelines. Europe: SolarPower Europe.

Triantaphyllou, E., Shu, B., Nieto Sanchez, S., & Ray, T. (1998). Multi-Criteria Decision Making: An Operations Research Approach. Encyclopedia of Electrical and Electronics Engineering, 175-186.

Varoquaux, G., & Colliot, O. (2023). Evaluating machine learning models and their diagnostic value. HAL Open Science, 1-31. https://hal.science/hal-03682454v4.

Velasquez, M., & Hester, P. (2013). An Analysis of Multi-Criteria Decision Making Methods. International Journal of Operations Research, 56-66. http://www.orstw.org.tw/ijor/vol10no2/ijor_vol10_no2_p56_p66.pdf.

Vujović, Ž. (2021). Classification Model Evaluation Metrics. (IJACSA) International Journal of Advanced Computer Science and Applications, 599-606. doi: 10.14569/IJACSA.2021.0120670.

Westphal, M., & Brannath, W. (2019). Improving Model Selection by Employing the Test Data. Proceedings of the 36 th International Conference on Machine Learning. Long Beach, California.

Yajure-Ramírez, C. (2023). Multi-criteria methodology based on data science for the selection of the optimal forecast model for residential electricity consumption. Scientia et Technica Universidad Tecnológica de Pereira.