1. Introduction
The objective of this article is to highlight the importance of a good coupling in a transmission line in which a through bandwidth will be propagated, as well as to identify the optimal and efficient coupling technique that can be implemented to have low decoupling losses. For this, it is necessary to understand the phenomenon that generates such losses and how to design and interpret the couplings that will correct such inconveniences, as well as to observe a real physical example of the problem and its respective implemented solution.
2. Theoretical Framework
The frequency variation present in a transmission line has always been a problem, since it contains all the secondary parameters of a transmission line, such as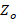 
, which is given by equation (1):
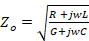
At zero frequency, the characteristic impedance reduces to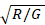 
, however, if the frequency is too high R and G become practically negligible against 
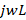and 
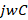, thus obtaining that the characteristic impedance reduces to 
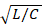. This is why, for high frequency variations, the characteristic impedance has a practically negligible change. On the other hand, the load impedance is affected by the frequency: the skin effect, in the resistive part, and its reactance which depends on the frequency. The reactance, either capacitive or inductive, at center frequency is given by equation (2):
where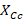 
and 
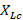are the capacitive and inductive reactance at center frequency, respectively. Therefore, when the frequency varies, high or low (x), the reactance is modified according to the equation (3):
where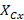 
and 
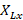are the capacitive and inductive reactance at frequency x (
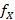), respectively. Combining equations 2 and 3 results in equation (4) as follows:
While for the real part of the impedance it is not so simple, since the skin effect is present. Therefore, the resistance will have a variation according to equation (5):
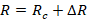
where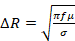 
, µ is the magnetic permeability of the material, σ is the conductance and ƒ is the frequency. The phenomenon that occurs in the apparent resistance of a material is due to the fact that at a certain frequency the charge has a uniform distribution over the entire area of the conductor; however, as the frequency increases, the magnetic field near the center of the cable increases the local reactance. The charge carriers move toward the edge of the cable, decreasing the effective area and increasing the apparent resistance (Hideshi, 2017). This effect is evident in Figure 1:
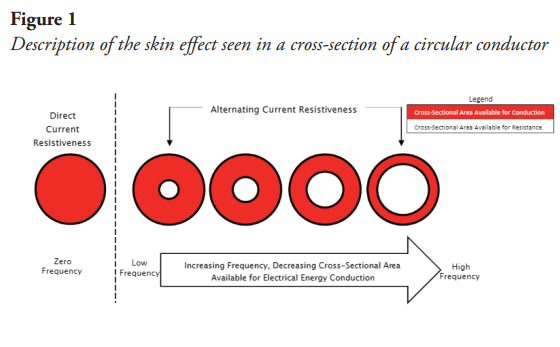
All these effects can be observed in cables typically used as transmission media, such as: coaxial cable, telephone pair or micro-tape line. According to a study by Walker and Wax (1946), the variation of resistance was found for three different references of a coaxial cable of reference RG-6, RG-8U and RG-58U, a telephone pair of reference CN 180 BR-500-ND and CN 170 BR-500-ND, and a micro-tape line of reference AF08-500-ND and AF06-500-ND.
As for the coaxial cable, which is generally used for high frequencies, because it has a decrease in its radiative losses and dielectric losses. The resistivity of the coaxial cable is given by equation (6):
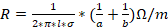
where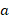 
is the radius of the solid center of the material, b the radius of the dielectric, 
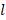the penetration depth (
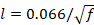) and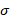 
the conductivity of the material.
For the RG-6 coaxial cable, the copper conductor material was identified, with radius of 0.37mm and conductivity of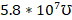 
; a polyethylene dielectric material with radius of 2.35mm (Pasternak, s. f.). The resistivity behavior of the coaxial cable is shown in Figure 2:
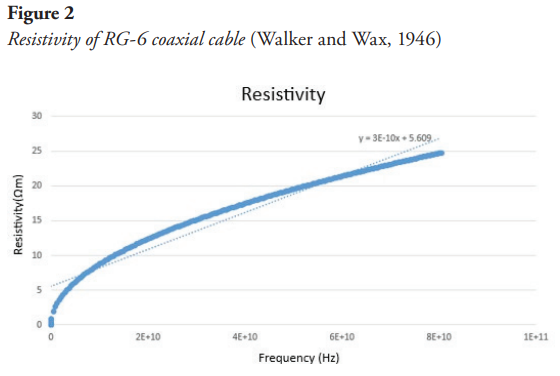
The telephone pair is another transmission medium consisting of a pair of conductors covered with a polyethylene insulating material and is twisted with the purpose of reducing the interferences produced by magnetic field induction with respect to the nearby pairs around it. The resistance of this medium is calculated by equation (7):
where is the conductor radius, l the penetration depth and 
the copper conductivity.
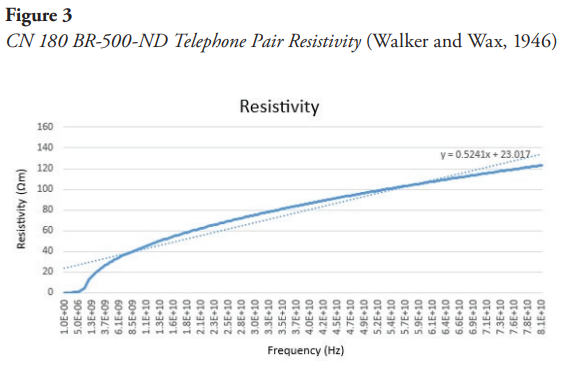
For the CN 180 BR-500-ND telephone pair with copper conductor material, radius of 0.38mm and conductivity of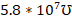 
(Digikey, s. f.), the resistivity behavior follows the curve in Figure 3:
While the micro-tape line has the characteristics of coaxial lines and waveguides, with a type of EM wave propagation. These lines are devices of much use in electronics since they allow according to their configuration to create various elements such as filters, resonators, couplers, antennas, among others. The resistance of the microstrip line is found with equation (8):
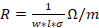
Where w the conductor width, l the penetration depth and σ the conductivity of the material.
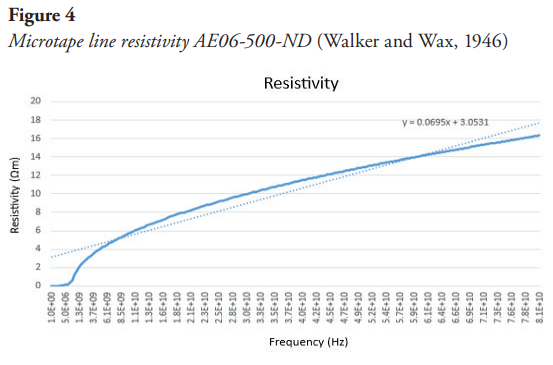
For the AE06-500-ND microtape line of copper conductor material, with a conductor width of 9mm and conductivity of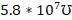 
(Digikey, s. f.), the resistivity behaves as shown in Figure 4:
Impedance variations trigger decoupling levels in transmission lines, which can be measured by means of the reflection coefficient or 
. The reflection coefficient, mostly known by 
o 
(Townsend, 1995), can be expressed by equation (9):
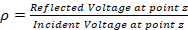
where the reflected voltage at any point z, is given by the expression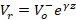 
and the incident voltage at any point z, is given by the expression 
; 
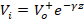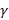is the propagation constant. If the reflection coefficient is evaluated at any point on the line, located on the Z axis, equation (10) is obtained:
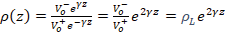
where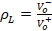 
can also be expressed as a function of impedances, as shown by equation (11):
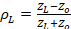
Note that, if the load is complex, the reflection coefficient will also be complex obtaining a phase shift (Townsend, 1995). On the other hand, the ROE is generally defined as a ratio of voltages, more specifically the maximum voltage over the minimum voltage of a voltage standing wave: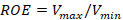 
(Townsend, 1995), where 
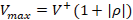and 
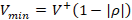. Hence, the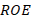 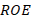simplifies to equation (12) (Rambousky, et al., 2015):
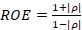
Analyzing the equations of the reflection coefficient and 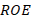, a range of operation for these can be established. In equation (11), 
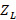can take three specific values (
, 
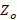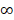y 0), it is known that if 
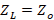we have a coupling condition, and replacing in the same equation we obtain 
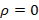. While if 
, 
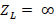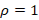and, if 
, 
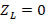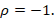These last two conditions, are known as maximum decoupling condition. On the other hand, analyzing 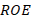with the range of variation of 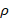, one can arrive at the statement that 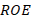will vary between 1 and .
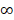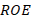and 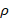are established as fundamental parameters when evaluating the level of decoupling in a transmission line for a bandwidth. Looking at 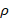, if it is non-zero, it means that 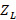is different from 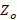and hence there is no coupling. Similarly, for 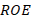, if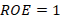 
, it means that 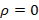and therefore there is a perfect coupling, otherwise, there is decoupling in the line.
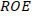can be measured in different ways, including the following: Directional 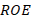meter or 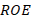bridge. The directional 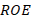meter has two terminals, a transmitter (TX) and the antenna (ANT), connected through an internal transmission line. This line is electromagnetically coupled to two smaller sensing lines (directional couplers) that terminate with resistors at one end and diode rectifiers at the other. The resistors are chosen to match the characteristic impedance of the sensing lines (Saber, 2019). The diodes are responsible for converting the incident and reflected wave magnitudes into DC voltages, FWD and REV respectively, as shown in Figure 5:
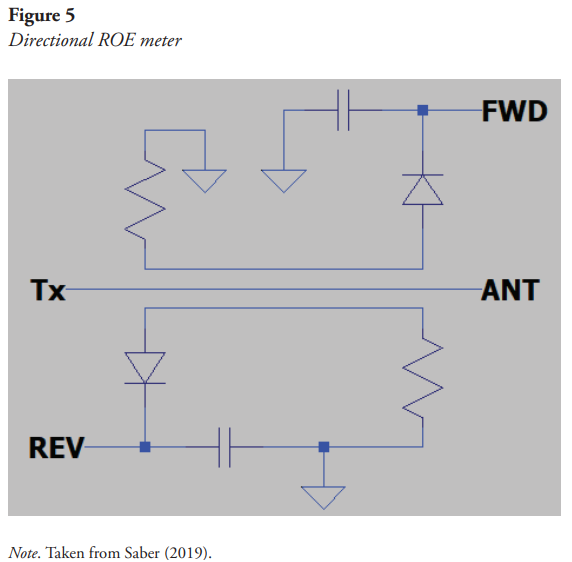
The 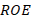bridge can be like a Wheatstone bridge, the bridge is balanced (0 volts across the detector) only when the test impedance exactly matches the reference impedance, while when a transmission line does not match (
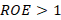), its input impedance deviates from its characteristic impedance obtaining a voltage difference at the output (Saber, 2019). The jumper indicates only decoupling but does not indicate impedance reading.
3. Methodology
For the design of the coupling techniques, the “Amanogawa” software was used as well as the impedance diagram also known as the Smith chart. In the first case, if there is a decoupled transmission line and it is of interest to couple it with a complex-valued load, a purely reactive element of equal magnitude and opposite sign to the load reactance is added (Townsend, 1995). However, it must be considered that, when eliminating such reactive part of the load impedance, it must be considered that the resistive component, both of the load impedance and characteristic, must be equal in order to obtain a maximum power transfer and therefore no reflected signal. For this purpose, a procedure is followed, considering the parameters of Figure 6:
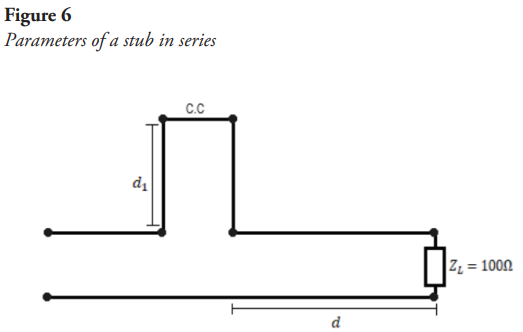
where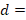 
distance at which the stub is located, 
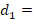stub length, 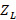= load impedance, 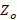= characteristic impedance of the transmission line. The procedure consists of:
- Locate the normalized load impedance on the Smith chart and plot the respective .
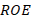- Move over the 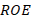the shortest distance until it intersects the circle of resistance
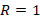. - Draw a straight line from the center of the circle to the cut.
- The value of d is the distance from
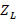to the above-mentioned cut-off in the direction towards the generator.
To ensure the coupling, the value of the stub reactance must be found with equation (13):
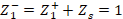
where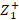 
is the impedance found with the circle cut-off 
. 
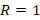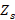is the normalized stub input reactance and 
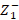is the impedance seen from the left of the stub insertion point:
is cleared.- The reactance semicircle
is located on the Smith chart.
The value of d1 is the distance from the intercept of the semicircle with the edge of the Smith chart circle, in the load direction, to the short circuit of the chart in terms of impedances.
Another technique used to minimize the decoupling of a line is the simple parallel stub: being in parallel with the other impedances the calculations are facilitated if one works in terms of admittances (Townsend, 1995). As in the previous case, the aim is to have a maximum power transfer, therefore, the impedance seen from the left at the insertion point of the stub must be equal to the characteristic impedance. For the design of a simple parallel stub, the parameters shown in Figure 7 are used as a starting point:
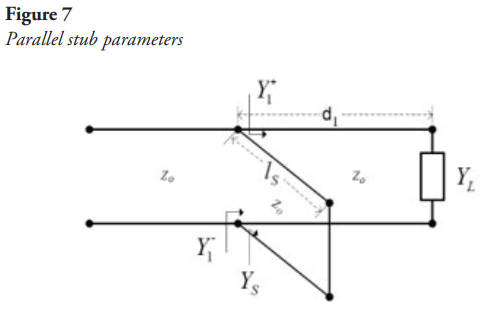
where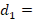 
distance at which the stub is located, 
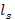= stub length, 
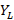= load admittance, 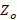= characteristic impedance of the line, 
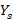= stub admittance, 
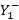= admittance to the left of the stub insertion point, 
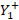= admittance of the stub at a distance 
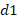from the load. The design follows the steps below:
- Locate the normalized load impedance on the Smith chart and plot the respective
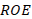. - Move over the 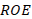a quarter lambda distance toward the load to find the normalized
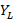. - Identify the circle
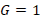and its respective intersection with the 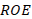circle. - Move
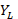towards the generator until the first intersection of 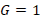with the 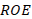circle is found to obtain the value of 
.
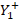To guarantee a coupling, it is required that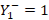 
. Therefore, equation (14) must be satisfied:
-
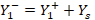
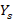is cleared to obtain its susceptance semicircle. - The stub length
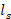is the segment between the short circuit in admittance and the susceptance semicircle 
.
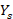Another way to solve the problem of a decoupled line is to insert a lambda-quarters section between the transmission line and the load. The section must measure lambda quarters and has its own characteristic impedance that depends on the primary parameters R (resistance), C (capacitance), G (conductance) and L (inductance). Since the impedances are in series, it makes it easier to work the Smith chart in terms of impedances. As in all previous cases, what is sought is to have a maximum power transfer, therefore, it must be fulfilled that the impedance seen from point b of Figure 8, is equal to the characteristic impedance:
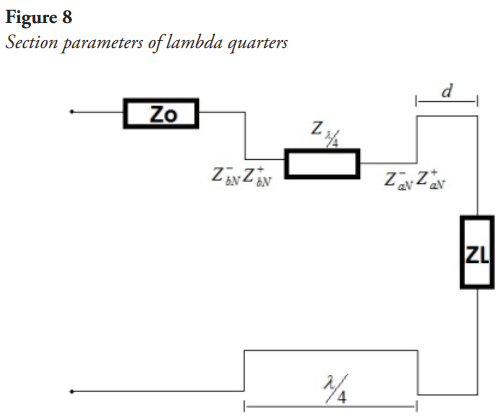
where 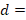distance at which the fourth lambda coupling section is located, 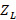= load impedance, 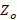= characteristic impedance of the line, 
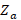= impedance of the section at point a, 
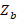= impedance of the section at point b. The following steps are followed for the design:
- Locate the normalized load impedance on the Smith chart and plot the respective
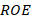. - Move over the 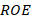towards the generator, until finding the real axis to obtain the normalized
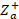(note that if 
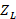is real, d will be equal to zero). - The value of d is the distance from 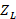to .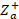
- We proceed to denormalize 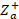with respect to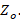
- Calculate the value of
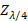with equation 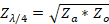(15).
(15)
To guarantee an effective coupling,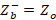 
must be fulfilled.
- Normalize
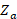with respect to 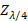. - Move
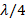towards the generator to find 
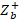. - Denormalize
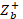with 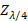to finally re-normalize 
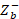with respect to 
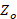. - Normalized 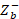should give approximate or equal to one, i.e.,
.
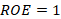Each coupling technique has its own limitations, such as the level of decoupling with frequency variation. In this article, impedance variations due to frequency variations are not considered; therefore, to find the level of decoupling due to frequency variations, the procedure is like that of the coupling for a central frequency, with the difference that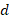 
and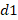 
are no longer found, now the displacements due to the change in frequency are made.
As the distance at which I place the stub is a function of lambda, and lambda is a function of frequency, any variation of this will cause changes in the designed coupling. This variation is known as decoupling and can be found as follows. The new values of ,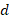 
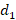and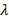 
for high and low frequency are calculated with equations (16) and (17):
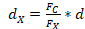
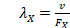
where X can represent H or L (high frequency or low frequency) and C represents the center frequency. Once the values of d and d1 are calculated, we start from the location of the normalized load impedance to move over its respective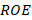 
towards the load a distance 
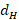and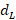 
, in this way we find 
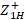and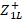 
.
Then with the value of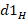 
and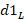 
, we start from the short circuit of the chart towards the generator a distance 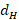and 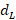, to find the value of 
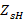and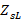 
respectively. As 
, 
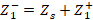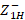and 
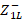are found to find the decoupling level by means of the 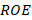and the reflection coefficient at that point. In the parallel stub there are also variations in the distances and lengths, since they depend on the frequency, therefore, starting from equation (16) the analogy can be made to find the new 
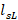and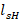 
, while with (17) the actual value of 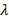is calculated.
Once the values of 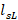and 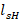are found, normalized 
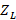, which has not changed is located again and its respective 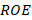is plotted; 
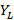is found. With equation (16) we fi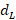nd and 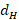to travel each distance on the circle of the 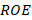to the generator, there we will find the value of 
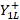and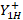 
respectively. With the values of 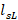and 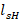, plot from the short on the Smith chart for admittances and find the respective 
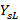and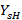 
. From equation (14) the values of 
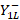and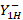 
are obtained to finally find the 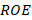and reflection coefficient on that point to evaluate the level of decoupling.
In the fourth lambda coupling section, there are also variations in the distances and lengths, since they depend on the frequency; therefore, d can be calculated from equation (16). While for the new value of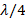 
we start from the equation of length of a wave (17).
Now with the value of , ,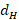 
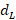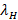and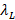 
calculated for the respective high and low frequency, normalized 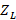, which has not changed, is located again and its respective 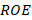is plotted. The respective translation is performed from 
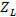a distance 
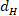and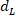 
to obtain the values of 
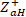and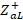 
. We proceed to denormalize each 
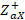with respect to 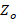to then be normalized again with respect to 
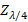. As it is already known 
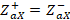, therefore, to find 
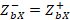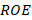, the of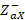 
is plotted and a length 
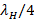and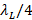 
is transferred in the direction of the generator. Already with the values of 
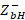and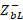 
, they are denormalized with respect to 
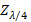to then be normalized again with respect to 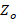and thus be located in the Smith chart in order to be able to calculate their new 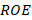, reflection coefficient and, therefore, their decoupling level.
In order to make the comparison, it was decided to implement the three couplings mentioned above in a single design, which is as follows; We have a transmission line with a characteristic impedance (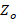) of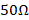 
and a load impedance with a value of 
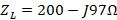, in a frequency range 
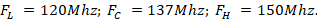For the parallel stub design, the procedure for the center frequency is performed as a first step.
Following the steps mentioned above, the load impedance value is normalized:
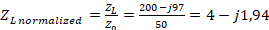
Then the normalized load admittance is found:
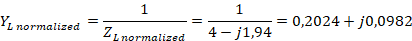
At this point the design tools are used, either the Amanogawa software application or the Smith chart. The next step is to locate the normalized load admittance and thus plot the value of the standing wave ratio better known as 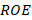or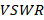 
, then perform the displacement from the normalized load admittance to the junction with 
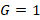to thus find the value of 
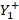. With a value of 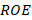equal to 4.9902, the distance d shifted from 
to 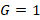corresponds to 
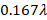; the arrival point allows finding 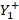, with a value of 
.
Then the value of the stub admittance is found: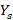 
, which corresponds to the complex imaginary conjugate of . 
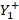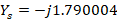is obtained. Since the stub ends in short circuit it must be moved from the short in admittance to the previously found value of 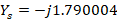, such distance corresponds to 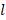(stub length) with a value of 
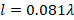. Assuming that the wave propagation is at the speed of light, the length would be 
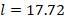cm. Finally, 
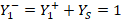is found, i.e., 
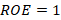and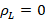 
.
Now the procedure is done for the high frequency (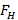
). As a first step the distance for high frequency is found as follows:
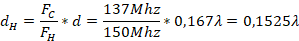
Following this we traverse this distance from the load to the generator to find 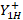, we obtain that 
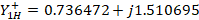; then we find the length 
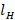as follows:
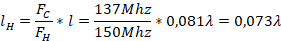
We move this length found above from the short in admittance on the circle 
(outer circle of the Smith chart) to obtain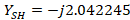 
. Finally, we find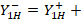 
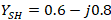. The respective 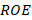and reflection coefficient at that point is: 
, 
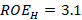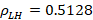. Which can be checked and observed by means of the software.
As a final step of the analysis the procedure for the low frequency (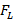
) is performed. First the normalized load admittance () is located, starting from this we proceed to move a distance 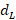by the 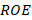in the direction of the generator, this distance is found as follows:
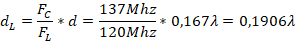
The displacement from the load admittance is performed, and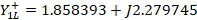 
is reached. Now the length of the stub: 
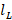, is found as follows:
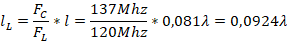
Then this length is shifted from the short in admittance on the circle 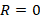to obtain 
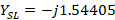. Finally,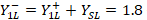 
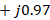is found with its respective 
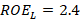and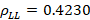 
. For the analysis of the series stub, we start with the center frequency (
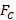). The first thing is to normalize the load impedance value:
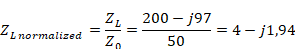
The normalized load impedance is in the impedance diagram and the displacement is made from it by its 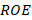to the intersection with 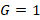in order to find the value of 
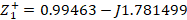. The distance at which the stub is located is found by finding the intercept with the circle of 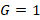, in this case it is obtained that 
.
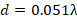Then, the value of the stub impedance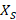 
is found, which corresponds to the complex conjugate of 
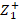, which gives: 
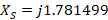. With this admittance, the stub length (
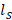) is found, moving along the circle 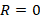from the short circuit in terms of impedance to the reactance semicircle 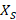, in the direction towards the load; 
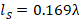is obtained. Finally, for , 
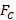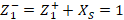is found with its respective 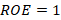and .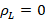
After that we continue with the procedure for the high frequency (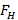): first we find the distance for high frequency as follows:
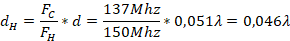
Then this distance from the load to the generator is traversed to find the corresponding value of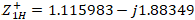 
. Now we proceed to find the length 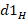as follows:
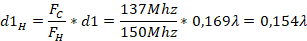
Therefore, this length is shifted from the short in impedance on the circle 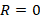thus obtaining 
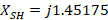. Finally, 
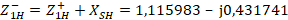and its respective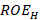 
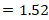and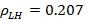 
are found. We continue with the procedure for the low frequency (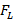). As a first step the normalized load impedance (
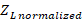) is located again, starting from this the displacement of a distance 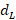by the 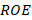in the direction towards the generator is performed. 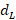is obtained as follows:
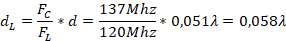
With this displacement we arrive at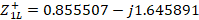 
. Now the length 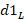is found as follows:
We then shift that length from the short in impedance about the circle 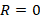and obtain 
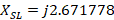. Finally,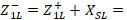 
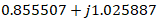is found along with its respective 
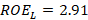and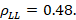 
For the fourth lambda section, we start with the norma-lized load impedance, already calculated in the previous designs:
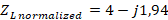
The normalized load impedance is located on the impedance diagram and the displacement from it by its 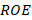to the intersection with the real axis is performed, in order to find the value of 
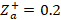. The distance at which the fourth lambda section is located is 
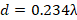. We proceed to calculate the value of 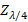, denormalizing 
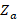with respect to 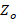, then:
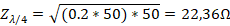
To verify the coupling, 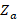is normalized with respect to 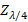, obtaining 0.448, and then 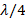is moved to the generator to find 
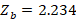, impedance that is denormalized with respect to 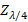. Finally, it is normalized again with 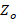and placed on the Smith chart to obtain 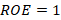and 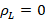. To evaluate the level of decoupling for high frequency (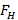), we first find: the distance and 
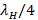for high frequency as follows:
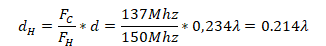
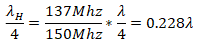
This distance from the load to the generator is now traversed to find the respective value of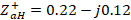 
. It is denormalized with respect to 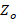and normalized again with :
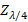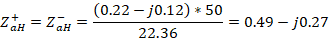
Then a length 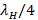is shifted to the generator to find 
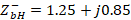; this impedance is denormalized with respect to 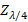, and normalized again with 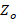, finding its respective 
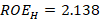and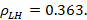 
The procedure to evaluate the decoupling level for the low frequency (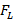) is as follows: the normalized load impedance (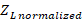) is located; we start from this to move a distance 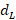by the SWR in the direction towards the generator: this distance is calculated as follows:
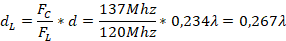
With this shift the value of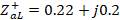 
is obtained. It is denormalized with respect to 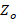and normalized again with .
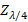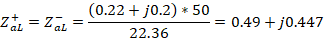
Then the equivalent 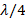length for low frequency is found as follows:
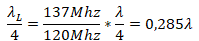
A length 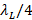is transferred to the generator to find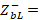 
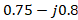; this impedance is denormalized with respect to 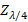and finally normalized again with 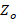, finding its respective 
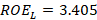and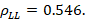 
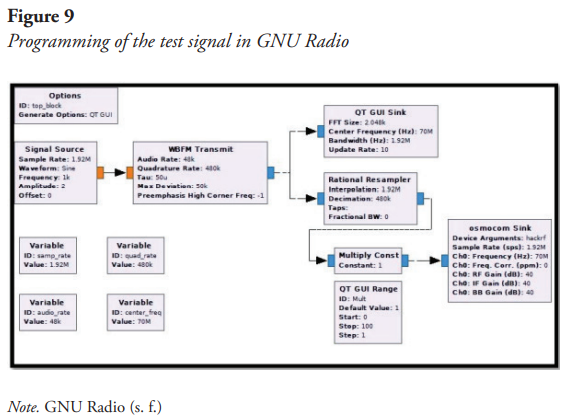
For the physical implementation of the narrowband impedance coupling, the one with the best performance in terms of bandwidth and lowest level of decoupling will be selected. According to the results presented below, the parallel stub coupling was selected: a reference RG - 6 coaxial cable, threaded connectors for RG - 6 cable and SMA adapters were used to perform the physical coupling. The test signal propagating in the line coupled by parallel stub is a 1KHz tone modulated on a 70 MHz carrier; an impedance with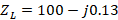 
value was used as load. The signal was extracted from the software defined radio module: HackRF ONE, programming in GNU Radio the blocks specified in Figure 9.
4. Results
By means of the Amanogawa software, the figures of the reflection coefficient (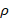) vs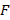 
of the three designs are obtained, which are shown in figures 10, 11 and 12 in the following table.
From figures 10, 11 and 12 it can be inferred that the decoupling for a parallel stub is not symmetrical between low frequency and high frequency. Comparing the three coupling techniques yields the characteristic features of each, which are shown in Table 1.
Figures 13 and 14 show the physical assembly and the evaluation of the decoupling level by means of the transmitted and received or dissipated signals in the load, from which the reflected signal is inferred. The measurements considered are the input voltage, corresponding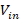 
(signal a in Figure 14) and the voltage over the load corresponding 
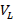(signal b in Figure 14).
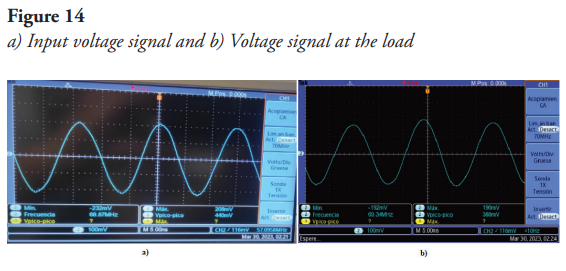
To find the reflected voltage and thus calculate the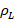 
, equations (19) and (20) were used, respectively:
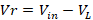
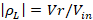
For the center frequency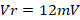 
, 
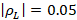and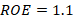 
were obtained; while for the high and low frequencies: 
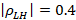and,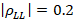 
were obtained.
5. Discussion of results
If the SWR and reflection coefficient parameters are considered as criteria for selecting the best narrowband coupling technique, the parallel stub technique is chosen because it presents lower SWR values for the frequencies located at the extremes (1.52 for high frequency and 2.91 for low frequency) of the through bandwidth. Also, the smallest magnitudes of the reflection coefficient for the frequencies located at the extremes of the passing bandwidth are evident in the stub in parallel (0.207 for high frequency and 0.48 for low frequency) (Middelstaedt, 2018). The evaluations of the parameters mentioned above, for the three coupling techniques, were made under the same conditions, namely, the same: load impedances, characteristic impedance of the line, through bandwidth, and attenuation equal to zero for the short length of the line.
However, the results of the stub in parallel showed the lowest levels of decoupling (see column 2 of table 1), the desired bandwidth of 30 MHz is not met for a maximum standing wave ratio of 1.4 at the two extreme frequencies of the through bandwidth (Adam, 2016). This standing wave value is recommended by national agencies, such as the National Spectrum Agency (ANE) in Colombia, for cell phone operators. The standing wave ratio of 1.4 corresponds to 1.7% reflected power and 98.3% transmitted power. The reflected power is the portion of incident power that was not absorbed by the load. The smaller the standing wave ratio, the better the load impedance will match the transmission line impedance or vice versa; although a standing wave ratio value of 1 is an ideal fit condition, it is unlikely to occur within normal design conditions.
Regarding the results of the decoupling level expressed in terms of the reflection coefficient and SWR, for a bandwidth similar to that used in the theoretical exercise (evaluated above), however, the central frequency, characteristic impedance of the line and the load impedance, values higher than the theoretical ones are obtained, due to the losses due to the welding points of the load, tolerance of the passive elements representative of the load impedance, and the attenuation of the signal due to coupling insertion losses and the measuring equipment.
In practice, the value of the standing wave ratio evaluated in the load for the extreme frequencies of a passing bandwidth can be altered by several factors. For example, in a radiant system, a damaged power cable or feeder, an inadequate or poorly connected connector, a splice of two misaligned line sections or an oxidized antenna port cause the impedance of the transmission line to vary throughout its entire length, and that the reflected wave increases. So, the value of the standing wave ratio will rise.
6. Conclusions
To conclude this article, it can be observed from Figures 5, 6 and 7 that the decoupling for any coupling technique is not symmetrical between the low frequency and the high frequency since it presents variations however small they may be. In addition, it is observed that the reflection coefficient graph of a parallel stub, unlike the series stub and lambda quarters, in the frequency range shown, does not reach the value of 1, which is the case of maximum decoupling.
Finally, it is observed that for both series and parallel stub, the frequency range to meet a ROE<0.2 is wider than in the lambda quarters section. Being the parallel stub even more practical, since it not only reaches an extreme case, but also is easy to fabricate and add, so it is fabricated with the same material of the transmission line.
