Uso del análisis de series de tiempo para pronosticar la producción de energía eléctrica de una planta solar fotovoltaica

1. Introducción

Existen dos principales factores, entre otros posibles, que explican en gran medida la necesidad del uso de fuentes renovables de energía para la producción de electricidad. Por una parte, la fuente primaria por lo general no tiene costo. Por ejemplo, para las plantas eólicas, la fuente primaria es el viento, y para las plantas solares fotovoltaicas la fuente primaria es la energía solar. Por otro lado, y según lo indicado en el reporte de la Agencia Internacional de Energía (IEA, 2022 por sus siglas en inglés) las fuentes renovables generan bajas emisiones de efecto invernadero. Por ello, la producción de energía eléctrica a través de fuentes renovables se ha ido incrementando con el tiempo, pues de acuerdo con el reporte de estatus global de energías renovables (Comunidad global de energías renovables REN21, 2022), para el año 2021, y a pesar de los retardos y las interrupciones en las cadenas de suministro producto de la pandemia COVID-19, se incorporaron a nivel mundial 314 gigavatios (GW) adicionales de capacidad instalada de energías renovables para la producción de electricidad, y de esos, 175 GW correspondieron a energía solar fotovoltaica.

La producción de una planta solar fotovoltaica conectada a la red (on-grid) se inyecta a la misma si se está a nivel de transmisión o distribución, pero si la planta es propiedad del usuario final, la producción podría satisfacer su demanda y los posibles excedentes se inyectarían a la red, si la normativa vigente lo permite. Cuando el objetivo de la planta sea abastecer zonas aisladas, la instalación estará desconectada (off-grid), y toda la producción iría para ese fin. Si los usuarios están conectados a la red, el pronóstico de la producción de energía eléctrica permitirá al propietario de la planta estimar sus ingresos en función de la producción esperada. En el caso desconectado, el pronóstico favorecerá el cálculo del nivel de carga que será satisfecho, así como los excedentes que podrían ser almacenados para su uso posterior. Asimismo, la predicción será útil para la planificación, gestión y operación de la planta, por lo que se deberán definir distintos horizontes para tales fines. El objetivo de esta investigación es desarrollar el pronóstico de generación de energía eléctrica de una planta solar fotovoltaica a través del análisis de series de tiempo para obtener los modelos de pronóstico, utilizando las escalas semanal y mensual. Específicamente, se obtuvieron cuatro modelos ARIMA (Autoregressive Integrated Moving Average) estacionales, dos en escala semanal y dos en escala mensual, y se utilizaron las siguientes métricas: error absoluto medio (MAE), raíz cuadrada del error cuadrático medio (RMSE) y el error porcentual absoluto medio (MAPE), para evaluar su desempeño y compararlos entre sí.

En torno a esto, se hizo una revisión del estado del arte relacionado con el área temática de esta investigación, al respecto, se encontraron diversos estudios, pero con horizontes de pronósticos diferentes y metodologías variadas. Por ejemplo, Vyas et al. (2022) desarrollaron un estudio para llevar a cabo el pronóstico de la energía eléctrica generada por una planta de 1 MW pico con datos diarios desde el año 2010 hasta el año 2022. Utilizaron un vector autorregresivo para el pronóstico correspondiente, y la métrica RMSPE para evaluar el desempeño de los modelos. Larson et al. (2016) realizaron el pronóstico diario de una planta solar fotovoltaica de 1 MW pico, ubicada en California, con un método basado en la optimización de mínimos cuadrados de la predicción meteorológica numérica (NWP). Las métricas utilizadas para evaluar el desempeño de los modelos fueron MAE, RMSE y el error medio de sesgo. Arias y Bae (2021) presentan un modelo de predicción utilizando herramientas para manejar grandes cantidades de datos, considerando datos históricos de irradiancia solar, eficiencia y características del sistema. Los mejores resultados correspondieron a 17,57 kW para el RMSE y 2,8 % para el error relativo medio. Kardakos et al. (2013) utilizan el análisis de serie de tiempo y las redes neuronales artificiales para llevar a cabo el pronóstico de corto plazo de la generación de una planta solar fotovoltaica. El primer modelo que emplean es uno estacional ARIMA, y el segundo es una red neuronal artificial con múltiples entradas. Para evaluar el desempeño de los modelos hacen uso del RMSE, normalizado con respecto a la capacidad instalada de la planta. Fara et al. (2021) aplicaron modelos ARIMA y red neuronal artificial para el pronóstico de la producción de energía de una planta solar fotovoltaica ubicada en el sur de Rumanía.

Los modelos obtenidos fueron comparados utilizando el MAE relativo y el RMSE relativo, resultando que los modelos ARIMA tienen mejor desempeño que la red neuronal artificial. Borunda et al. (2022) hacen uso del aprendizaje automático para obtener modelos de pronóstico de la producción de energía eléctrica fotovoltaica, y la mejor ubicación posible de la planta solar fotovoltaica. Samanta et al. (2014) consideran la regresión lineal tradicional, la regresión de soporte vectorial y los modelos ARIMA, para desarrollar el pronóstico de la irradiancia solar y, por consiguiente, la energía eléctrica, para diferentes horizontes de pronóstico en el corto plazo. Para evaluar el desempeño de los modelos hacen uso de la métrica RMSE. Jung et al. (2022) manejan un modelo de vector autorregresivo para el pronóstico regional de plantas solares fotovoltaicas en Corea del Sur. Estos autores utilizan el valor normalizado del RMSE y el coeficiente de determinación para evaluar el modelo.

Gaikwad y Agravat (2017) desarrollaron una metodología para el pronóstico diario de energía eléctrica proveniente de la energía solar y la energía eólica. Utilizaron modelos ARIMA y redes neuronales artificiales, además de un software de pronóstico de variables climáticas para obtener los datos de estas variables, que luego fueron usadas en los modelos para calcular el pronóstico de la energía eléctrica. Konstantinou et al. (2021) utilizan una metodología basada en red neuronal recurrente para el pronóstico horario de la producción eléctrica de una planta solar fotovoltaica ubicada en Chipre. El desempeño del modelo fue evaluado utilizando el RMSE y la validación cruzada k-fold, obteniendo un valor de 0,11368 que disminuye a 0,09394 cuando se aplica k-fold. Fan et al. (2022) desarrollan un modelo combinando tres técnicas de pronóstico: análisis de serie de tiempo con modelos ARIMA, red neuronal artificial y regresión de soporte vectorial, que emplearon para pronosticar la producción de energía de una planta solar fotovoltaica. Las métricas de comparación utilizadas fueron el MAE, el MSE y el MAPE. Concluyen que su modelo tiene mejor desempeño que los que se generan con las tres técnicas aplicadas de manera individual.

El resto del artículo se organiza de la siguiente manera. En la sección 2 se presenta la metodología utilizada en la investigación y en la sección 3 se examinan los resultados obtenidos luego de aplicar la metodología. Seguidamente, se exponen las conclusiones de la investigación, y por último, se presentan las referencias bibliográficas utilizadas.

2. Metodología

En esta investigación se aplica la metodología de los proyectos de ciencia de datos la cual, según Vanderplas (2017), es un área interdisciplinaria que está compuesta a su vez por tres áreas. Cuando se combinan dos de ellas, el manejo adecuado de matemáticas y estadística para modelar conjuntos de datos, y el dominio o habilidad sobre el área de investigación de la cual provienen los datos, se llega a lo que es la investigación tradicional. Pero, al agregar a estas dos, la habilidad computacional para diseñar y usar algoritmos para procesar, almacenar y visualizar grandes cantidades de datos, se obtiene lo que se conoce como ciencia de datos.

Los proyectos de ciencia de datos constan de una serie de etapas, que según Cielen et al. (2016), son el establecimiento de objetivos, la extracción u obtención de datos, su procesamiento, el análisis exploratorio, la modelación de los datos y la toma decisiones basada en los conocimientos adquiridos. Para el procesamiento se tiene un conjunto de técnicas cuyo uso dependerá del caso particular que se esté tratando. De acuerdo con Navlani et al. (2021), estas técnicas podrían incluir: manejo e imputación de datos faltantes, manejo e imputación de datos atípicos, manejo de datos duplicados, escalado y/o transformación de variables, entre otras. Para el análisis exploratorio de los datos se podrían utilizar técnicas estadísticas descriptivas, gráficos univariados y/o multivariados, entre otros. Al final de la etapa de análisis exploratorio, se pudiera haber encontrado conocimiento importante para el análisis (insights), así como patrones en los datos a considerar en la siguiente etapa. Posteriormente, en la etapa de modelación se aplican los algoritmos necesarios para obtener los modelos matemáticos a utilizar para la generación de conocimiento útil. El tipo y cantidad de algoritmos a utilizar dependerá de los objetivos planteados en la etapa inicial y, probablemente, de los resultados del análisis exploratorio.

La etapa de modelación en esta investigación consiste en aplicar el análisis de serie de tiempo para obtener modelos ARIMA que se utilizan luego en el pronóstico. En específico, se aplica la metodología Box-Jenkins descrita y utilizada por Cryer y Chan (2008) para generar modelos ARIMA, y presentada detalladamente por Makridakis et al. (1997). Esta metodología está compuesta por tres fases y aplica tanto a series estacionarias como no estacionarias: una primera fase de identificación, que incluye a su vez dos pasos: la preparación de los datos y la selección del modelo inicial. En la preparación usualmente se transforman los datos para estabilizar la varianza y/o se diferencian para hacer la serie estacionaria. La selección de los modelos potenciales se hace examinando los datos con gráficos y técnicas estadísticas descriptivas, y haciendo uso de las funciones de autocorrelación y autocorrelación parcial. La segunda fase, de estimación y prueba, incluye también dos pasos: estimación y diagnóstico. En el primero se estiman los parámetros de los modelos potenciales, y se selecciona el mejor de estos utilizando un criterio de comparación determinado, el cual usualmente es el AIC (Akaike Information Criteria), pues según Mills (2019): “Hay una variedad de criterios de selección que se pueden utilizar para elegir un modelo apropiado, de los cuales quizás el más popular es el de Akaike” (p. 28). En el diagnóstico se hace el análisis de los residuos para verificar que se cumpla con los supuestos estadísticos. En caso de ser afirmativo, se pasa a la fase de aplicación, en la que se usa el modelo para realizar el pronóstico requerido.

En esta sección se presentan las etapas de obtención y procesamiento de los datos, mientras que las etapas restantes se exponen en el siguiente apartado.

2.1. Modelo ARIMA y métricas de evaluación de desempeño

2.1.1. Análisis de Serie de Tiempo

En este tipo de análisis la idea es conocer el valor futuro de una variable objetivo, sin intentar descubrir los factores que afectan su comportamiento. Supone que los patrones históricos de la variable se repetirán más adelante, y por tal razón se busca identificar esos patrones. Existe una variedad de modelos para el análisis de series de tiempo, y uno de los más conocidos son los modelos ARIMA. Estos están compuestos por una parte autorregresiva (AR), una parte de promedios móviles (MA) y la parte integrativa (I).

En la parte autorregresiva (AR), la variable objetivo en el instante de tiempo t, depende de sus valores retardados en el tiempo, tal como se muestra en la ecuación (1), en la que se observan hasta p retardos:

$Y_t=b_0+b_1\bullet Y_{t-1}+b_2\bullet Y_{t-2}+\dots +b_p\bullet Y_p+e_t$     (1)

En la componente de promedios móviles (MA), las variables explicativas corresponden a los errores pasados, tal como se presenta en la ecuación (2), en la que se tienen hasta q retardos en los residuos:

$Y_t=b_0+b_1\bullet e_{t-1}+b_2\bullet e_{t-2}+\dots +b_q\bullet e_q+e_t$    (2)

Al combinar las ecuaciones 1 y 2 se obtienen los modelos ARIMA que se pueden aplicar a series estacionarias. Si se quiere aplicar el modelo a series no estacionarias deberá diferenciarse (I) la serie correspondiente d veces, en donde el valor d final dependerá de la serie en cuestión. De esa manera, se completa el modelo ARIMA (p, d, q). Según Hammad et al. (2020), los modelos ARIMA fueron propuestos por primera vez por Box y Jenkins en 1976.

Ahora, si la serie además de ser no estacionaria (d≠0) presenta estacionalidad, se deberá generar un modelo que considere esta característica. El modelo final quedaría entonces como ARIMA (p, d, q) (P, D, Q). En donde P, D y Q tienen el mismo significado que las correspondientes letras en minúsculas, pero considerando los valores estacionales de los datos.

2.1.2. Métricas de evaluación de desempeño de los modelos

Para efecto de evaluar los modelos de pronóstico y hacer comparaciones entre ellos se utilizan una serie de métricas. De acuerdo con Makridakis y Hyndman (1997) entre las medidas estadísticas estándar para evaluar modelos se tienen: el error absoluto medio (MAE), la raíz cuadrada del error cuadrático medio (RMSE) y el error porcentual absoluto medio (MAPE). Siendo el error, la diferencia entre el valor real y el valor pronosticado. A continuación, se presentan las ecuaciones matemáticas utilizadas para calcular estas métricas:

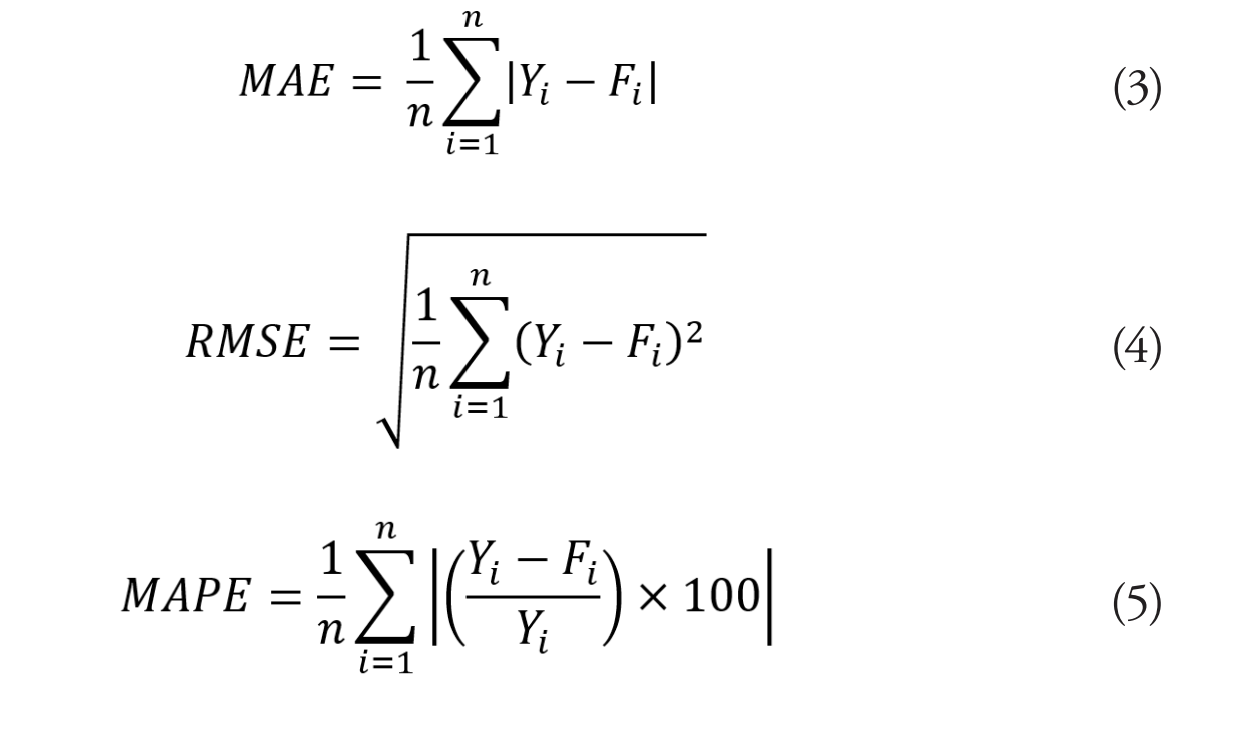
Siendo:

Y_i: El i-ésimo valor medido de la variable a pronosticar, y que sería Y_t  en caso de serie de tiempo.

F_i: El i-ésimo valor pronosticado.

n: Número de registros o datos históricos disponibles.

2.2. Obtención de los datos

Para esta investigación los datos se extrajeron de la página web del conjunto de datos públicos del Laboratorio Nacional de Energías Renovables (NREL, por sus siglas en inglés), y corresponden al sistema de adquisición de datos de una planta solar fotovoltaica del NREL ubicada en Golden, Colorado (PVDAQ NREL, 2023). Esta planta está compuesta por cinco paneles solares marca Sanyo, con celdas de monosilicio y 200 vatios de potencia pico (SolarDesignTool, 2023), instalados en un montaje fijo, con 40° de inclinación y ángulo azimut de 180°.

El set de datos consta de cinco variables (columnas), y son mediciones ejecutadas y guardadas cada minuto, de potencia pico de salida de la planta (“ac_power”), en vatios, temperatura ambiente (“ambient_temp”) en grados Celsius, irradiancia (“poa_irradiance”) en vatios por metro cuadrado, velocidad del viento en metros por segundo (“wind_speed”) y tasa de suciedad (“soiling”). Los datos van desde el 25 de febrero del 2010 hasta el 13 de diciembre del 2016, siendo un total de 1.558.875 filas (registros o instancias).

2.3. Procesamiento de los datos

El primer paso consiste en utilizar la variable de potencia eléctrica para generar una nueva variable con los datos de energía eléctrica generada (“ac_energy”). Por otra parte, se detectó que para el año 2010 no existen registros en los meses de enero, septiembre y octubre, por lo que para el análisis se consideraron los registros desde el mes de noviembre del año 2010 en adelante, que totalizan 1.473.570 filas. Por otro lado, debido a que se trabajará con escalas temporales diferentes a los minutos, se suman los valores de energía minutales dentro de cada hora, día, semana y mes, para obtener datos con escala horaria (25.780 registros), diaria (2.200 registros), semanal (320 registros) y mensual (74 registros), respectivamente.

3. Discusión de resultados

A continuación, se presentan el análisis exploratorio de los datos y su respectiva modelación, así como la correspondiente discusión de resultados.

3.1. Análisis exploratorio de los datos

Se exponen a continuación distintas curvas que muestran el comportamiento de la energía generada por la planta solar fotovoltaica, junto con la irradiancia solar que es captada por los paneles de la planta. En la Figura 1 se presentan las curvas horarias de las dos variables mencionadas de manera previa. Realmente se presenta el intervalo de confianza de ambas variables, al 5 % de significancia estadística.

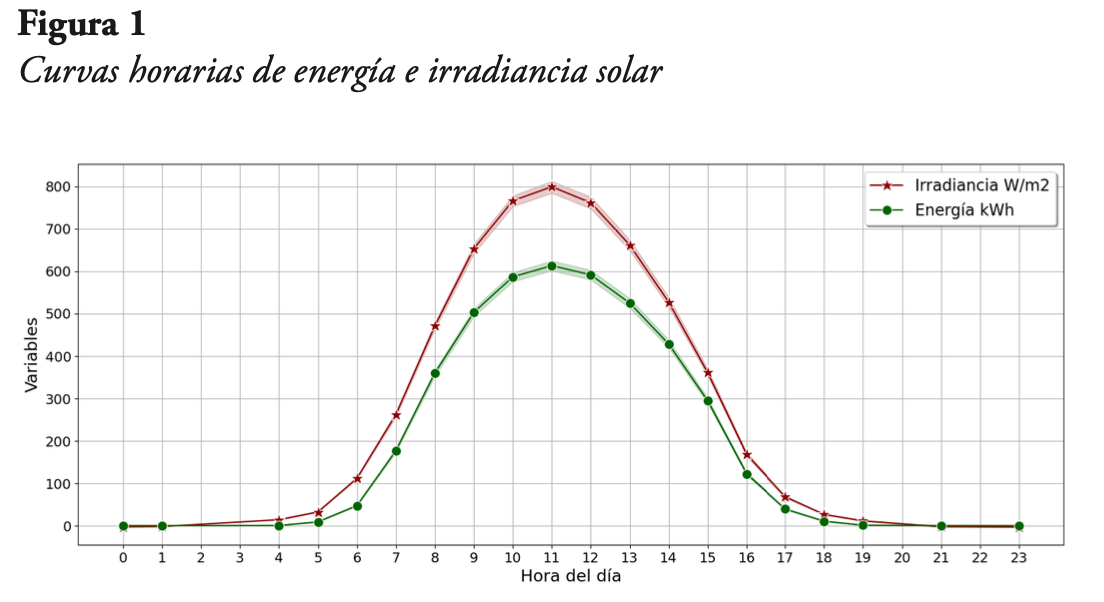
De la Figura 1 se puede ver, como era de esperarse, que la irradiancia solar inicia con valores bajos al inicio de la mañana, luego se incrementa de manera constante hasta llegar a su valor máximo alrededor de las 11 a. m., seguidamente inicia el descenso de sus valores, hasta hacerse nulos al final de la tarde. La curva de energía eléctrica tiene exactamente el mismo comportamiento. Asimismo, se puede notar que, en cada hora del día, la dispersión de los datos de irradiancia solar es significativamente baja, al igual que el de la energía eléctrica generada.

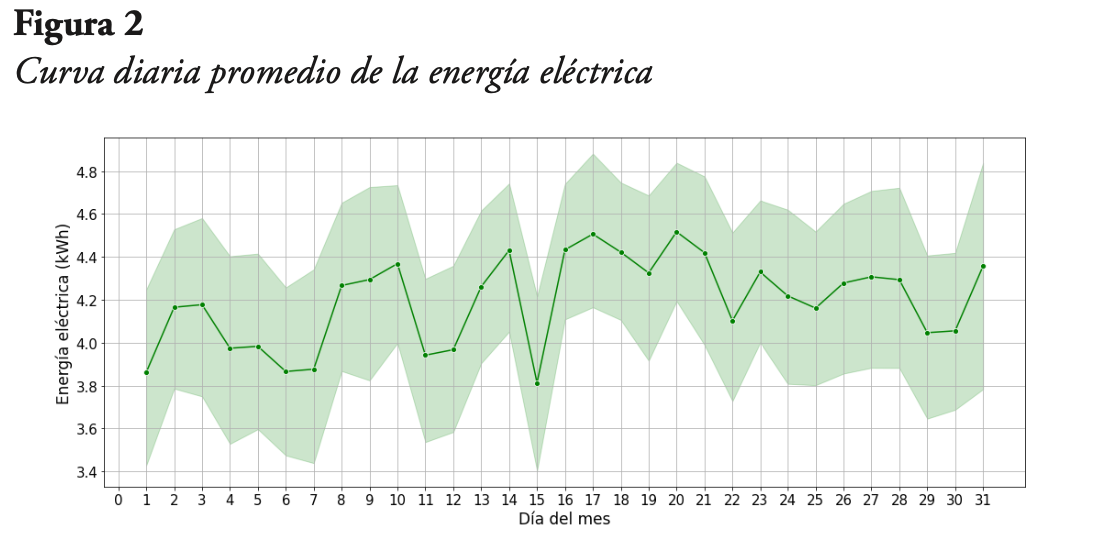
Seguidamente, en la Figura 2 se presenta la curva promedio diaria de la energía eléctrica generada, junto con su intervalo de confianza al 5 %. Se puede observar que los datos presentan una alta variabilidad con respecto a su valor medio, con su valor mínimo ocurriendo en el día 15 del mes, luego sube y alcanza su valor máximo el día 21. Por otra parte, también se nota que la curva no tiene ningún tipo de tendencia.

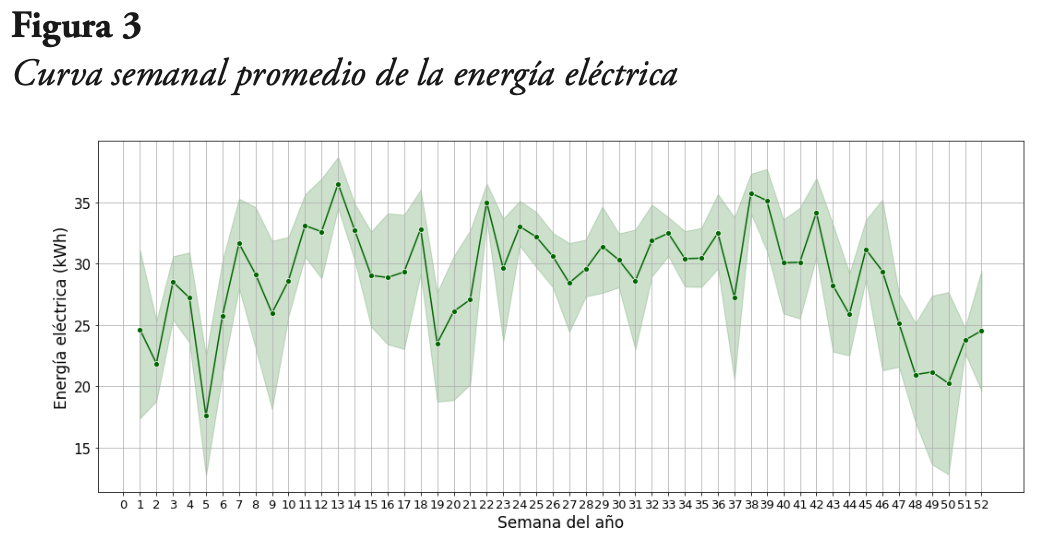
Ahora, en la Figura 3, se muestra la curva semanal promedio de la energía eléctrica generada, de la que se observa que tampoco evidencia algún tipo de tendencia. Sin embargo, se puede ver que la generación de energía cae en un período que va desde finales de año hasta inicios del siguiente año. El valor máximo promedio ocurre en la semana 13 del año, mientras que el valor mínimo promedio ocurre en la semana 5 del año.

En cuanto a los datos mensuales, estos se tomaron de la energía generada, y corresponden a todos los meses que tenían la información completa. Estos datos se graficaron junto con el valor de irradiancia solar promedio, lo cual se presenta en la Figura 4. Se puede notar que ya a escala mensual el comportamiento de la curva de energía no es tan parecido al comportamiento de la curva de irradiancia solar. De igual forma, se observa la existencia de una estacionalidad anual en la curva de energía eléctrica, con valores mínimos entre los meses de noviembre y diciembre, lo que coincide con lo encontrado en la Figura 3.

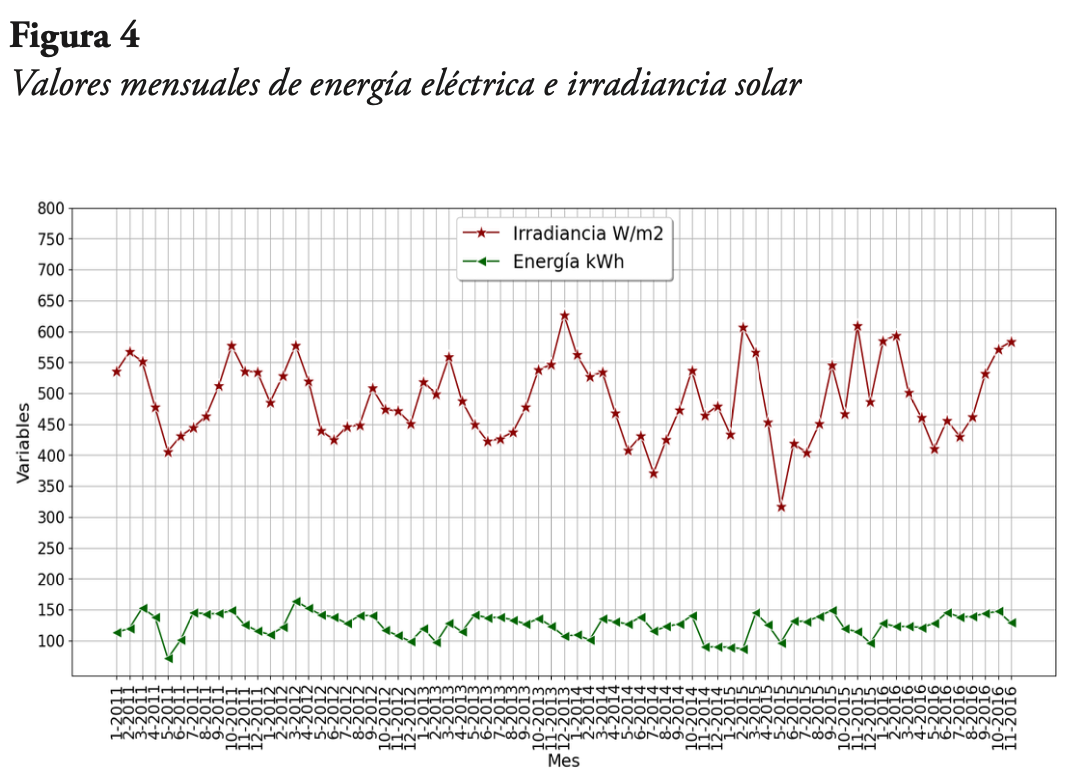
Con respecto al comportamiento de los datos de energía eléctrica comparado con los datos de irradiancia solar, se tiene que mientras la escala temporal sea más pequeña (cercana a la escala minutal original), las dos variables se comportan de manera similar. Para corroborar lo anterior, en la Tabla 1 se presentan los valores del coeficiente de correlación entre este par de variables, para las distintas escalas temporales consideradas tomando en cuenta tres métodos para el cálculo de los coeficientes, el de Pearson que es un método paramétrico, y los de Spearman y Kendall que no son paramétricos (Haslwanter, 2016).

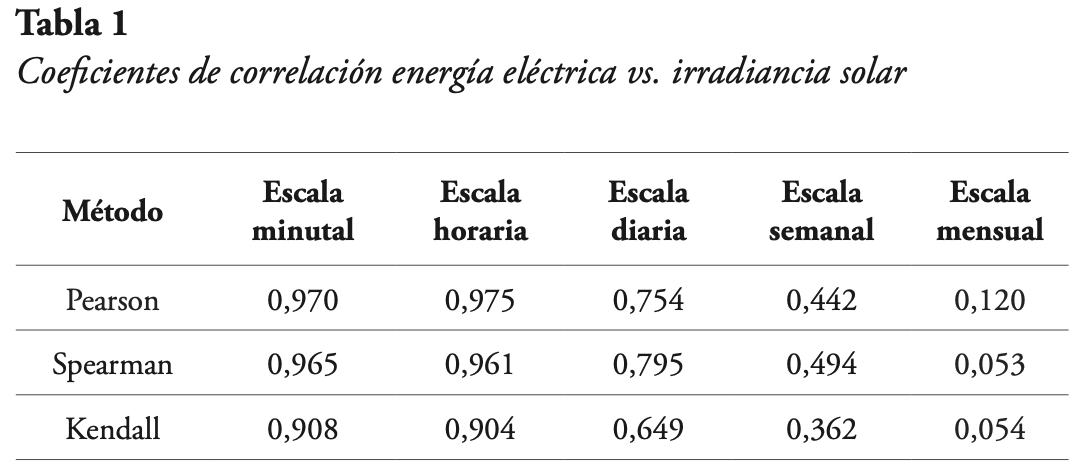
Es importante recordar que, según lo que indican Bruce y Bruce (2017), el coeficiente de correlación varía entre -1 y 1, siendo igual a 1 cuando hay una correlación positiva perfecta entre el par de variables consideradas, mientras que si vale -1, hay una correlación negativa perfecta. Un valor de cero indica que no hay correlación alguna entre las variables. De acuerdo con los resultados mostrados en la Tabla 1, tanto en la escala minutal como en la escala horaria, los valores de correlación son bastante cercanos a la unidad, para cada uno de los tres métodos. Pero a medida que la escala de tiempo es mayor, los valores de correlación van disminuyendo, hasta llegar a valores casi nulos de correlación para la escala mensual.

3.2 Modelación de los datos

En este apartado se aplica la metodología Box-Jenkins para obtener los modelos ARIMA que nos permitirán realizar el pronóstico de la generación eléctrica producida por la planta solar fotovoltaica. Se obtienen modelos ARIMA utilizando los datos semanales para realizar el pronóstico, luego se repite el proceso, pero utilizando datos en escala mensual.

3.2.1. Aplicación de metodología Box-Jenkins – escala semanal

Para efectos de aplicación de la metodología Box-Jenkins, se considera la serie de tiempo semanal de energía eléctrica generada, desde la semana 41 del 2010 hasta la semana 26 del 2016, es decir, 299 registros. Los datos desde la semana 27 del 2016 hasta la semana 48 del mismo año se utilizan para realizar el pronóstico y comparar con los valores reales.

Ahora bien, como se observó en la Figura 3, los datos semanales no presentan tendencia de ningún tipo, pero sí estacionalidad anual (cada 52 semanas). La estacionariedad se confirma al aplicar la prueba de Dickey-Fuller ampliada para detección de raíces unitarias, la que de acuerdo con Afriyie et al. (2020) tiene como hipótesis nula que la serie bajo estudio tiene al menos una raíz unitaria. Se aplicó la prueba a la serie en nivel, es decir, sin diferenciarla, y a la serie diferenciada estacional. Los resultados se muestran en la Tabla 2.

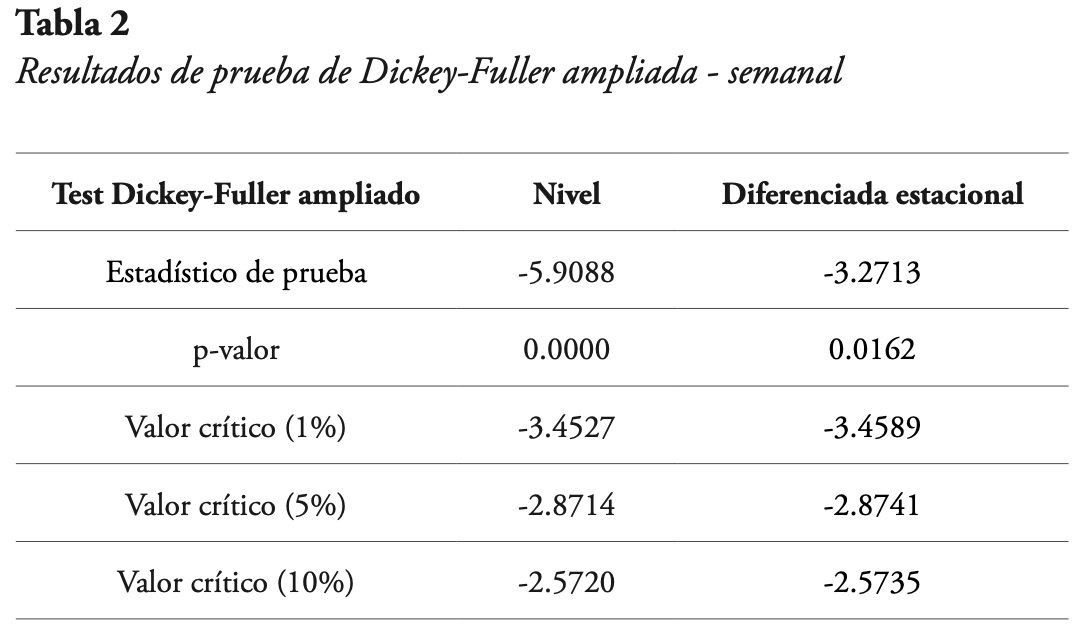
De la Tabla 2 se puede ver que, para la serie de nivel, el p-valor es menor al 1 %, por lo que se rechaza la hipótesis nula de que la serie tiene raíces unitarias, además de ello, el estadístico de prueba es menor para cada uno de los valores críticos. Por todo lo anterior, se puede decir que la serie de nivel es estacionaria. En cuanto a la serie diferenciada estacional, se observa que el p-valor es menor al nivel de significancia del 5 %, pero mayor al nivel de significancia del 1 %, es decir, la hipótesis nula se rechaza para el 5 %, pero no para el 1 %. Esto se comprueba al notar que el estadístico de prueba es mayor al valor crítico del 1 %.

El siguiente paso consiste en graficar las funciones de autocorrelación y autocorrelación parcial, con el fin de determinar un modelo inicial. Esta información se encuentra en la Figura 5. Se puede ver que la serie en nivel tiene un valor autorregresivo estacional (SAR), así como componentes autorregresivos (AR) en nivel.

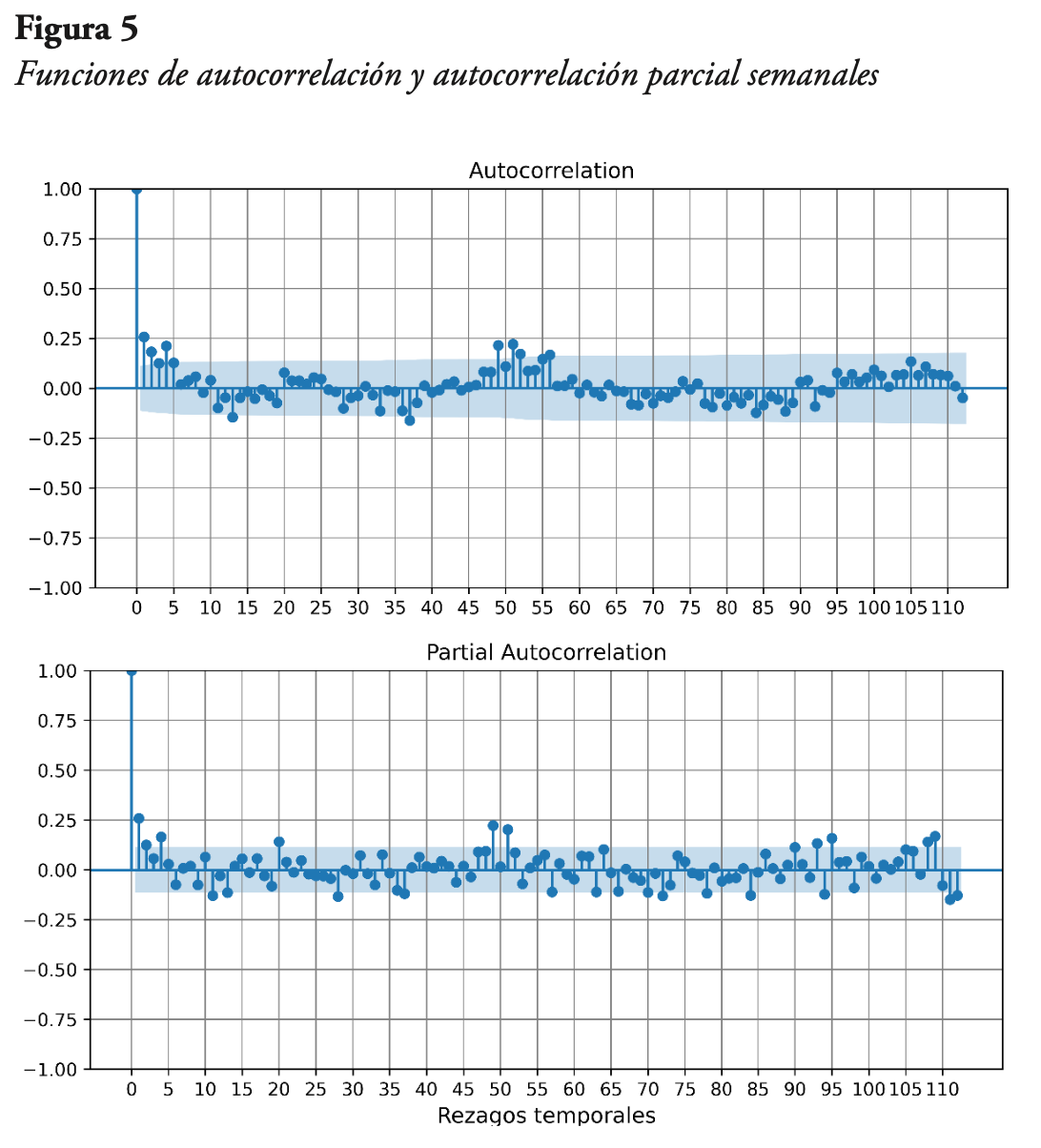
Tomando en cuenta los resultados obtenidos a partir de la Figura 5, se prueban varios modelos y se seleccionan aquellos que minimizan el AIC, pero que además cumplan con los supuestos estadísticos para los residuos. En ese sentido, se seleccionaron dos modelos: el primero de ellos es el ARIMA (1,0,1) (1,1,2) [52] y el segundo es el ARIMA (1,0,0) (1,1,0) [52]. Es decir, en ambos casos predomina la parte estacional, con una componente autorregresiva y una raíz unitaria, pero en la parte estacional del primer modelo, también hay dos componentes de promedio móvil. Por otra parte, en el primer modelo se tiene una componente autorregresiva, y otra de promedios móviles en la serie de nivel, y en el segundo modelo solo una componente autorregresiva en la serie de nivel.

Con respecto al análisis de los residuos, en ambos modelos se aplica la prueba de Ljung-Box cuya hipótesis nula indica que las autocorrelaciones de los residuos son nulas. Según Mahan et al. (2015), la prueba de Ljung-Box es útil para probar la autocorrelación de los residuos, considerando más de un rezago. También se aplica la prueba de Jarque-Bera, cuya hipótesis nula dice que la asimetría y el exceso de curtosis son nulos, es decir, se distribuyen normalmente. De acuerdo con Ahmad y Khan Sherwani (2015), la prueba de Jarque-Bera es muy popular para probar normalidad, y tienen buen desempeño para tamaños de muestras similares a las de esta investigación.

Considerando la prueba Ljung-Box, para el primer modelo se obtuvo un p-valor de 0,58 superior al 5 % de significancia estadística, y para el segundo modelo el p-valor fue de 0,83. Para ambos casos se puede decir que los residuos son independientes. Ahora, considerando la prueba de Jarque-Bera, para el primer modelo se obtuvo un p-valor de 0,09 y para el segundo modelo el p-valor fue de 0,19. Por lo anterior, para ambos casos se puede decir que los residuos están normalmente distribuidos.

3.2.2. Aplicación de metodología Box-Jenkins – escala mensual

Para la aplicación de la metodología de Box-Jenkins a los datos mensuales, se considera la serie de tiempo mensual de energía eléctrica generada, desde el mes de octubre del 2010, hasta el mes de junio del 2016, es decir, 69 registros. Los datos desde julio del 2016 hasta noviembre del mismo año se utilizan para realizar el pronóstico, y comparar con los valores reales de energía eléctrica.

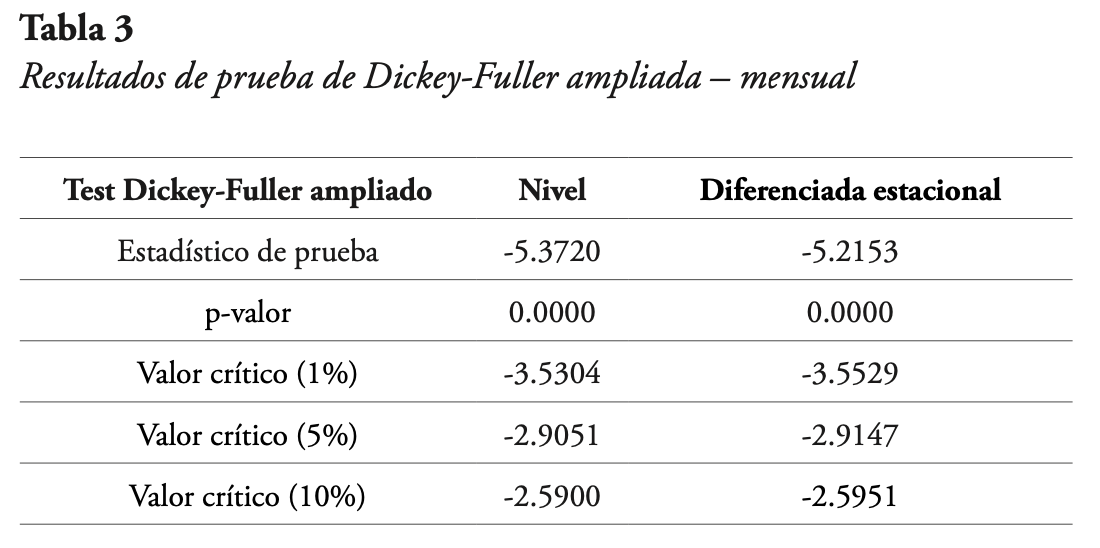
De acuerdo con lo observado en la Figura 4, existe estacionalidad anual en los datos (cada 12 meses), con valores mínimos entre los meses de noviembre y diciembre. Adicionalmente, de la misma figura se puede apreciar que los datos no tienen tendencia, y aparentemente tienen baja variabilidad. Para verificar lo anterior, se aplica la prueba de Dickey-Fuller ampliada a la serie en nivel, y a la serie diferenciada estacional. Los resultados se presentan en la Tabla 3. Puede verse que tanto el p-valor de la serie de nivel como el de la serie diferenciada estacional son iguales a cero, por lo que se puede decir que ambas series son estacionarias, de acuerdo con esta prueba.

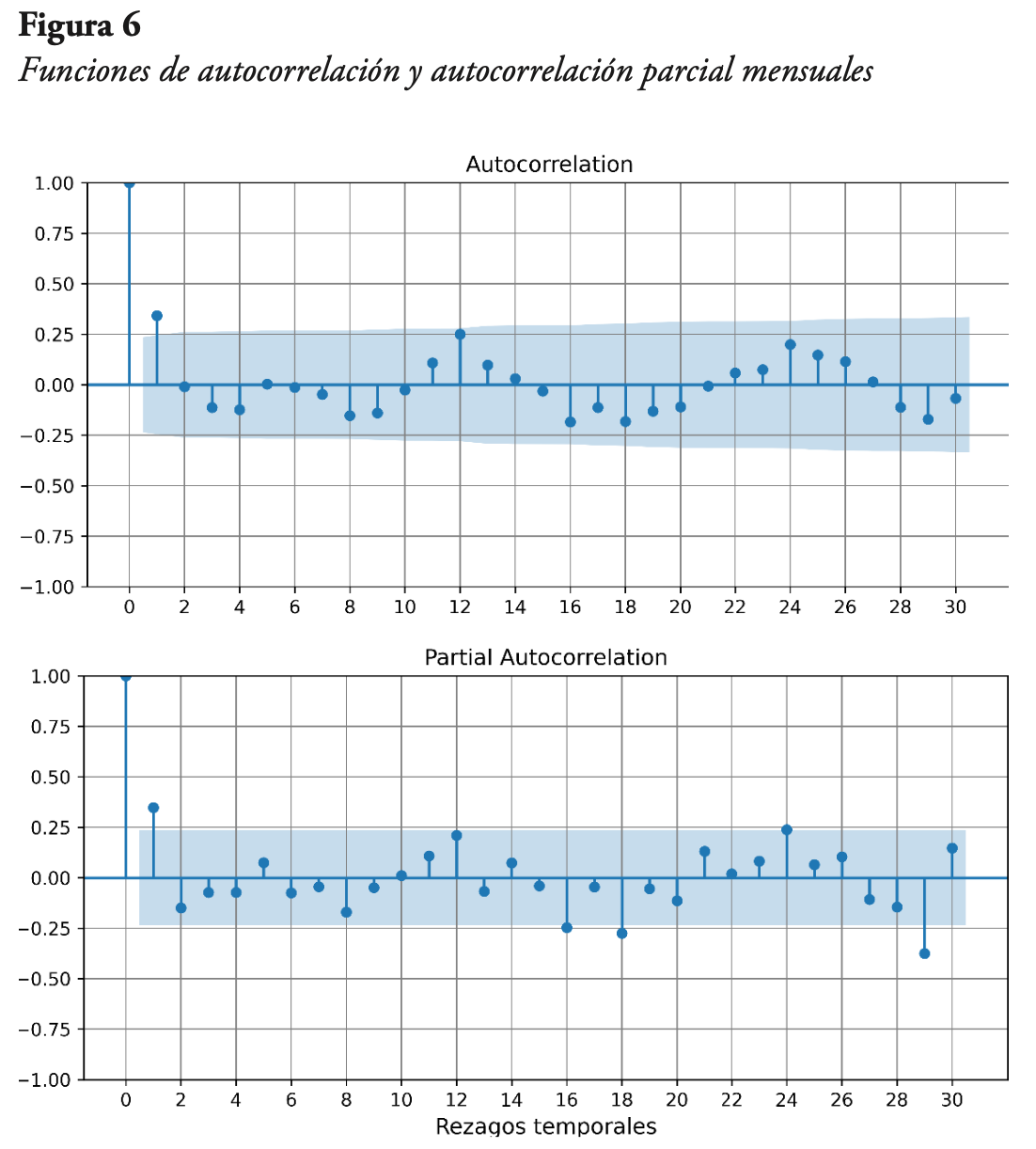
Posteriormente se graficaron las funciones de autocorrelación y autocorrelación parcial de la serie de nivel, las cuales se presentan en la Figura 6. Se puede ver que en ambas figuras hay un valor significativo para el primer rezago, y que luego los valores se comportan de manera sinusoidal, lo que sugiere una componente AR y otra MA en la serie de nivel. Asimismo, se puede notar que, en la función de autocorrelación parcial, los valores múltiplos de 12 se mantienen constantes, mientras que, en la función de autocorrelación, los valores múltiplos de 12 disminuyen exponencialmente, lo que sugiere una componente autorregresiva estacional.

Con los resultados obtenidos hasta ahora, se procedió a probar varios modelos ARIMA, seleccionando aquellos que minimizan el AIC, pero que además cumplan con los supuestos estadísticos para los residuos. Así, se consideran dos modelos, el primero de ellos es ARIMA (1,0,2) (1,0,1) [12] y el segundo es el modelo ARIMA (0,0,1) (1,0,0) [12].

Tomando en cuenta la prueba Ljung-Box, para el primer modelo se obtuvo un p-valor de 0,73 y para el segundo un p-valor de 0,96, por lo cual se puede decir que los residuos en ambos casos se distribuyen de manera independiente. En cuanto a la prueba de Jarque-Bera, en ambos casos el p-valor fue superior al 5 % de significancia estadística: 0,57 para el primer modelo y 0,27 para el segundo, por lo que se puede decir que los residuos están normalmente distribuidos para ambos casos.

3.2.3. Comparación de resultados de los pronósticos

Con los datos semanales, se realizaron pronósticos para las semanas de la 27 a la 48, y se compararon con los valores reales, calculando las métricas de desempeño MAE, RMSE y MAPE. En la Tabla 4 se muestran los resultados obtenidos para cada uno de los dos modelos. Se puede observar que el primer modelo tuvo el mejor desempeño, puesto que tiene los valores mínimos de cada una de las tres métricas consideradas.

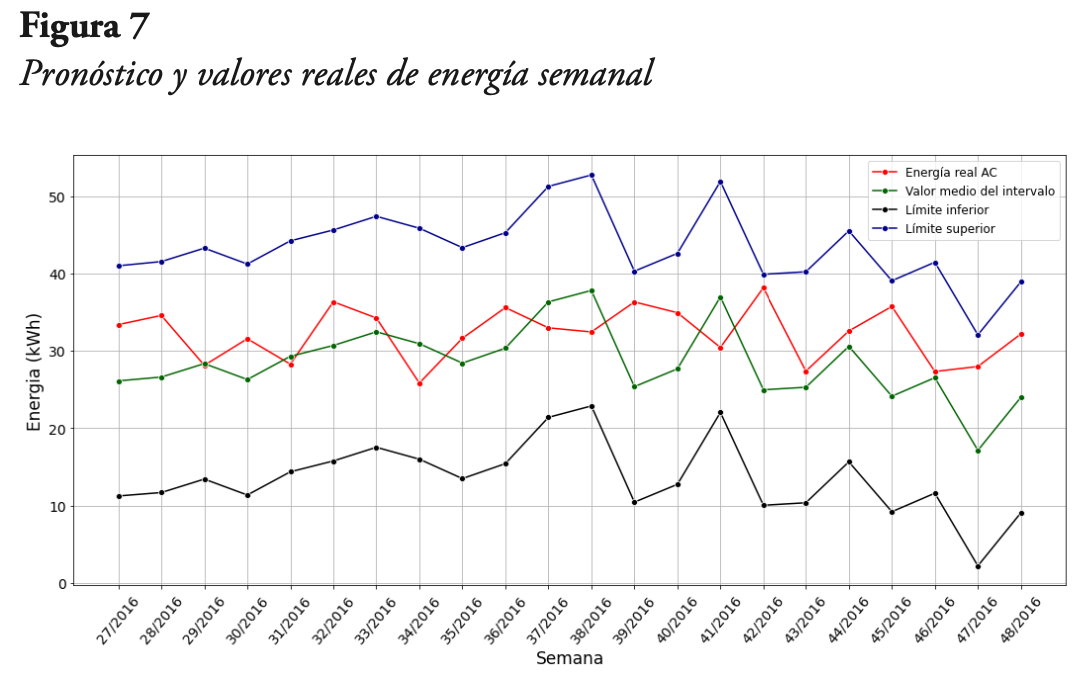
Ahora bien, los valores de pronóstico obtenidos corresponden al valor medio del intervalo de confianza al 5 % de significancia estadística. En la Figura 7 se presenta el intervalo de confianza mencionado, para el primer modelo semanal, junto con los valores reales de energía. En primer lugar, se observa que los valores reales de energía caen dentro de los límites del intervalo de confianza. Adicionalmente, se aprecia que los valores de la curva promedio coinciden o están cerca de los valores reales, para las semanas 29, 31, 33, 43, 44 y 46.

Por otra parte, con los datos mensuales se realizaron pronósticos para los meses de julio a noviembre del año 2016, período que es equivalente al utilizado en el pronóstico semanal. Los resultados se compararon con los valores mensuales reales, y se calcularon las métricas MAE, RMSE y MAPE. En la Tabla 5 se muestran los resultados obtenidos, de los cuáles se puede ver que el primer modelo tiene mejor desempeño, de acuerdo con las métricas utilizadas.

Con respecto al MAPE, que es una métrica porcentual, se obtuvo que, de los cuatro modelos presentados para el mismo período de tiempo, dos en escala semanal y dos en escala mensual, el primer modelo mensual es el que tiene menor valor, con un 8,31 %. En la Figura 8 se presenta el pronóstico obtenido con este modelo, junto con los valores reales de energía mensual.

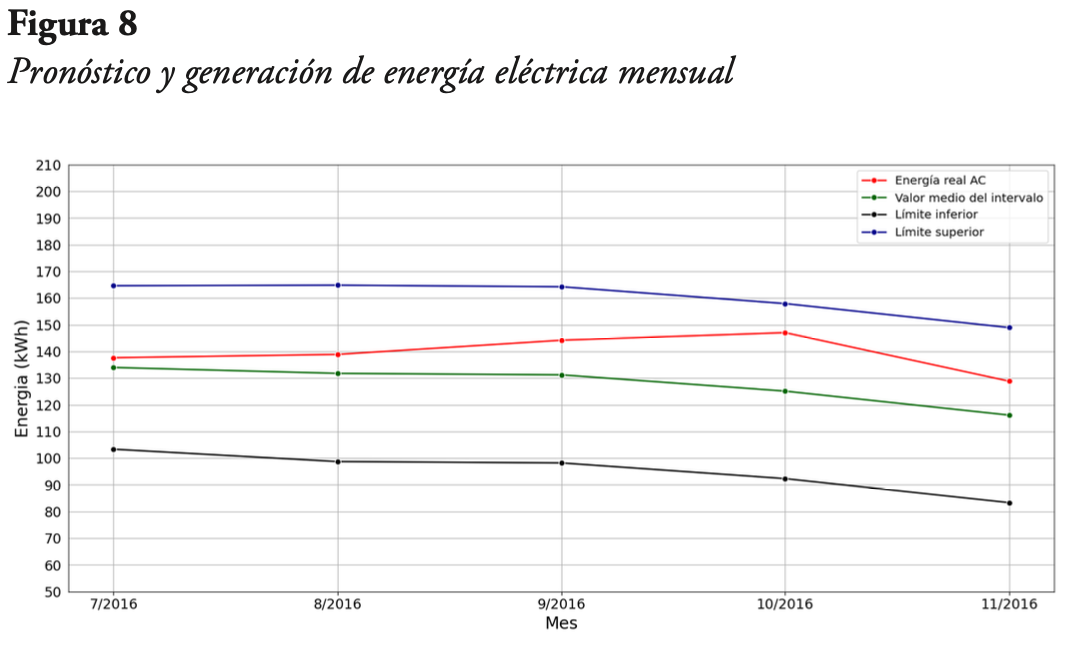
De la Figura 8 se evidencia que los valores reales de energía caen dentro del intervalo de confianza de la predicción. Además, se observa que estos valores reales son siempre superiores al valor medio del pronóstico, es decir, caen en la banda superior del intervalo de confianza.

4. Conclusiones

En esta investigación se hace uso de los modelos ARIMA del análisis de series de tiempo para el pronóstico de la energía eléctrica generada por una planta solar fotovoltaica, considerando resoluciones temporales semanal y mensual.

En los modelos ARIMA semanales hay fuerte presencia de estacionalidad, con la existencia de una raíz unitaria estacional. Del análisis de los residuos se puede decir que no están correlacionados, y además están normalmente distribuidos. En cuanto a los modelos mensuales, también se presenta la estacionalidad anual, pero no hay raíces unitarias ni de nivel ni estacionales. De los resultados de las pruebas correspondientes, se deduce que los residuos están no correlacionados, y que, a su vez, siguen una distribución normal.

De los dos modelos semanales, el primero fue el que tuvo mejor desempeño en el pronóstico realizado, pues tuvo los valores mínimos de las métricas de desempeño consideradas. Con respecto a los modelos mensuales, también el primero tuvo los valores mínimos de las métricas. De los cuatro modelos, el primer modelo mensual fue el que tuvo el menor valor de la métrica MAPE con un 8,31 %.

La curva real de energía eléctrica generada cae dentro del intervalo de confianza del pronóstico respectivo. Para el caso semanal, la curva promedio de los pronósticos está más cerca de la curva real, en comparación con el caso mensual, en el que la curva real está cerca del límite superior del intervalo de confianza al final del período de pronóstico.

En los datos con escalas diaria, semanal y mensual no se observa algún tipo de tendencia, lo cual queda verificado con los resultados de la prueba de Dickey-Fuller ampliada aplicada a los datos semanales y mensuales. Además, el comportamiento de las curvas de energía eléctrica generada es similar al comportamiento de las curvas de irradiancia solar, a excepción de la curva con datos mensuales. Lo anterior queda confirmado con el análisis de correlación entre esas dos variables.