Uso de algoritmos de Machine Learning para analizar los datos de energía eléctrica facturada en la Ciudad de Buenos Aires durante el período 2010–2021

1. Introducción

El análisis de datos de consumo y/o facturación de energía eléctrica, así como los datos de número de usuarios, son importantes desde el punto de vista de todos los actores del sector eléctrico de distribución, ya que permiten definir políticas desde los organismos del Estado y mejorar la gestión del servicio que se presta desde las empresas distribuidoras de electricidad. Por ejemplo, los organismos reguladores del sector eléctrico podrían implementar políticas de uso racional y eficiente de la energía eléctrica con base en al análisis de los datos de consumo de energía eléctrica, por tipo de usuario, utilizando como proxy de consumo la energía eléctrica facturada. Por otra parte, las empresas distribuidoras podrían “incentivar” menos consumo en los meses donde la facturación es ‘mayor’, pero la disponibilidad de energía es menor (o viceversa); en todo caso, se puede verificar si los incentivos ya implementados están funcionando de la manera adecuada. De manera similar, se pueden tomar medidas con antelación para evitar sobrecargas de la red producto de los picos de demanda estacionales. Con este fin, debe haber una coordinación total entre los organismos del Estado y las empresas distribuidoras de energía eléctrica para la implementación de las políticas públicas del sector eléctrico. Por citar, en el informe técnico de segmentación de la Subsecretaría de Planeamiento Energético del Ministerio de Economía de Argentina (2022) para el establecimiento o rediseño de los subsidios a los usuarios residenciales se indican los escenarios de cooperación necesarios para implementar esta política pública.

Las empresas distribuidoras que suplen energía eléctrica a la Ciudad de Buenos Aires, capital federal de la República de Argentina, son la Distribuidora de Energía Sur (Edesur) y la Distribuidora y Comercializadora de Energía Norte (Edenor). De acuerdo con un documento de trabajo del año 2016 de la Subsecretaría de Escenarios y Evaluación de Proyectos del Ministerio de Energía y Minería (MINEM), los picos de demanda de energía en Argentina están relacionados con las altas temperaturas en el verano y las bajas temperaturas en el invierno, con un mayor impacto de las temperaturas del verano. De igual manera, MINEM (2016, p. 9) indica que en lo que respecta a la demanda de energía asociada a las distribuidoras del área metropolitana de Buenos Aires, “la estacionalidad de la demanda está influenciada principalmente por los clientes residenciales, mientras que los grandes clientes comerciales y los industriales, no presentan variaciones significativas en su demanda a lo largo del año”. Aunque el documento de trabajo del MINEM es del año 2016, a partir del análisis de datos de esta investigación se espera ratificar estos resultados.

Los tipos de usuarios del servicio eléctrico se podrían clasificar como: usuarios residenciales, usuarios comerciales, usuarios industriales, usuarios oficiales, y otros usuarios fuera de estas categorías. En ese sentido, la proyección de la población de la Ciudad de Buenos Aires es según la Dirección General de Estadística y Censos (DGEyC, 2022) de 3.081.550 habitantes. Adicionalmente, para el año 2019, y de acuerdo con el censo de locales comerciales, se contaba con un total de 130.480 locales en los que se comercializan servicios o mercancía para la venta al público. La DGEyC (2022) también indica en sus estadísticas que el consumo de energía eléctrica del sector industrial en la ciudad de Buenos Aires para el año 2020 fue similar en promedio al consumo del año 2001, pero que para el año 2021 este consumo de energía en promedio creció un 6 %. Sin embargo, el consumo de energía eléctrica del año 2021 aún estuvo por debajo del consumo del año 2019. En cuanto al consumo por parte de los usuarios oficiales en la Ciudad de Buenos Aires, en el año 2020 cayó alrededor de 13 % con respecto al año 2019, pero para el año 2021 se incrementó casi 40 % con respecto al año anterior.

Como se mencionó previamente, las altas temperaturas del período de verano podrían impactar la demanda de energía eléctrica, y por ende su facturación; es así como según Infobae (2022), el pasado 14 de enero del 2022 hubo un récord de demanda de energía eléctrica debido al incremento de la temperatura hasta los 40 °C en varios puntos del país, incluyendo la Ciudad de Buenos Aires. De igual forma, de acuerdo con Ámbito (2021) durante el período de invierno del año 2021 se produjeron los récords de demanda de energía de invierno, en la Ciudad de Buenos Aires, con Edesur, alcanzando el pico de demanda el 28 de junio, al igual que Edenor.

En la presente investigación, tomando en cuenta los datos estadísticos oficiales de la DGEyC (2022) de Buenos Aires, se realizó el análisis de los datos de energía eléctrica facturada mensual por tipo de población usuaria y público usuario del servicio eléctrico durante el período 2010-2021. El propósito fue describir, a partir de los resultados cuantitativos obtenidos, sus características principales y, además, descubrir patrones en la energía eléctrica facturada que permitan ratificar la estacionalidad del consumo de energía en la Ciudad de Buenos Aires. Adicionalmente, se buscó determinar cuáles eran las variables del conjunto de datos que tienen un mayor impacto sobre la energía total facturada. Con este fin se hizo uso de algoritmos de Machine Learning, tanto de aprendizaje supervisado como no supervisado. Específicamente, se utilizó el algoritmo K-Means para encontrar patrones en los datos de energía eléctrica facturada, el análisis de componentes principales para reducir la dimensionalidad de los datos previo a la aplicación de algoritmos supervisados, y el algoritmo de regresión lineal múltiple para generar un modelo que permita predecir los valores de energía total facturada.

Luego de realizar una revisión bibliográfica relacionada con el tema, no se encontraron investigaciones similares a la aquí desarrollada, pues la mayoría está orientada al consumo eléctrico residencial y/o al uso de algoritmo K-Means para definir perfiles de usuarios. Guzmán y Sánchez (2021) elaboran un análisis exploratorio de los datos del servicio público domiciliario de energía eléctrica de la ciudad de Bogotá, capital de Colombia, el cual tuvo como objetivo desarrollar un modelo de aprendizaje automático que ayude a predecir potenciales suscriptores morosos. De igual manera, Marrero et al. (2021) utilizaron el algoritmo de aprendizaje no supervisado K-Means para clasificar perfiles de clientes residenciales del sur de Chile, utilizando los datos provenientes de los medidores inteligentes instalados en los hogares de estos clientes. Del conjunto de 1179 medidores inteligentes, obtuvieron dos clústers, uno de alto consumo, y otro de consumo menor. De la misma forma, Morales et al. (2022) utilizan dos algoritmos de agrupamiento (K-Means y Agrupamiento Jerárquico) para identificar diferentes perfiles de consumidores de energía eléctrica, utilizando datos de consumo de energía eléctrica de la región oriental del Paraguay almacenados entre enero del 2017 y diciembre del 2020. Por otra parte, Rajabi et al. (2019) desarrollaron un estudio de comparación de técnicas de agrupamiento para segmentación de patrones de carga eléctrica utilizando datos provenientes de medidores inteligentes manejados por la Comisión de Regulación de Energía de Irlanda. Finalmente, Hosseini y Fard (2021) realizaron un estudio para modelar los factores que afectan el consumo de energía eléctrica en edificios utilizando algoritmos de Machine Learning. Específicamente, usaron algoritmos de árboles de decisión, bosques aleatorios y K-vecinos más cercanos.

El resto del artículo se organiza de la siguiente manera. En la sección 2 se presenta una serie de conceptos básicos para comprender de mejor forma la metodología utilizada. Seguidamente, en el acápite 3, se presenta la metodología utilizada. En el apartado 4 se exponen los resultados obtenidos. Finalmente, se plantean las conclusiones que se derivaron de la investigación realizada.

2. Marco teórico

Algoritmos de aprendizaje

En principio, se puede decir que un algoritmo está conformado por una serie de pasos que tienen como objetivo resolver un problema. Es decir, la existencia de problemas que se repiten en distintas situaciones crea la necesidad de crear algoritmos que resuelvan estos problemas con el uso, por lo general, de herramientas matemáticas y computacionales. En ese sentido surgieron los algoritmos de aprendizaje, entendiéndose por aprendizaje lo planteado por Shalev-Shwartz y Ben-David (2014, p. 1): “el aprendizaje es convertir la experiencia en habilidad y/o conocimiento”.

Los algoritmos de aprendizaje han existido desde hace varias décadas, pero no habían sido tan utilizados debido a la complejidad de las operaciones matemáticas que están detrás del uso de estos algoritmos, las cuales requieren una alta capacidad de cómputo. Por ejemplo, Arthur Samuel, a inicios de la década de 1950, cuando trabajaba en la empresa IBM, diseñó un algoritmo que permitió a una computadora de la época jugar “Damas” contra él y vencerlo. El aprendizaje de la computadora evolucionó de tal manera que permitió que dos computadoras jugaran entre sí (Fenner, 2020). El gran logro de Samuel no fue que las computadoras jugaran “Damas”, sino que las computadoras aprendieran a jugarlo.

En la actualidad, con el desarrollo vertiginoso de la computación y la informática los algoritmos de aprendizaje se implementan con facilidad en distintas áreas de interés: academia, investigación de mercado, detección de fraudes bancarios, detección de usuarios morosos en el sector eléctrico, entre otras. Los algoritmos de aprendizaje se conocen también como algoritmos de “Machine Learning” que es la terminología utilizada en el idioma inglés; es así como Lee (2019, p. 1) define Machine Learning como “una colección de algoritmos y técnicas utilizadas para diseñar sistemas que aprenden a partir de datos disponibles. Estos sistemas son entonces capaces de desarrollar predicciones o deducir patrones a partir de otros datos suministrados”. Es importante destacar que la implementación de estos algoritmos incluye el uso de técnicas de programación y el uso de conocimientos de matemáticas y estadística. Además, asociado al concepto de Machine Learning está el de Ciencia de Datos, que de acuerdo con Cielen et al. (2016, p. 1) “involucra el uso de métodos para analizar cantidades masivas de datos y extraer el conocimiento que contienen”. Estos métodos a los que refiere esta definición de la Ciencia de Datos son precisamente los algoritmos de Machine Learning, los cuales, usualmente, se dividen en tres categorías: algoritmos de aprendizaje supervisado, algoritmos de aprendizaje no supervisado y algoritmos de aprendizaje reforzado.

Algoritmos de aprendizaje supervisado

Consisten en algoritmos de aprendizaje que requieren que el sistema sea entrenado entregando un conjunto de datos de entrada y el correspondiente conjunto de datos de salida con el fin de generar el modelo de predicción o de clasificación. Paluszek y Thomas (2019) indican que el aprendizaje es supervisado debido a que el conjunto de entrenamiento es establecido por una persona, es decir, esta persona, ejerciendo el rol de “Maestro”, le informa al sistema cuál es la salida deseada para un conjunto de elementos de entrada. El proceso de clasificar las salidas del sistema para un conjunto dado de las entradas se conoce como “etiquetamiento”, en el sentido de que se indican cuáles salidas del sistema son las correctas para cada conjunto de entradas.

Existe una variedad de algoritmos de aprendizaje supervisado, unos caen dentro de la categoría de Regresión y otros en la categoría de Clasificación, y se utilizará uno u otro dependiendo del caso de estudio que se esté considerando. Entre los algoritmos de aprendizaje supervisado más conocidos se tienen: Regresión Lineal (Simple o Múltiple), Regresión Logística, K-NN o K-vecinos más cercanos, Bayes Naive, Máquina de Soporte Vectorial, Árboles de Decisión y Bosques Aleatorios.

Algoritmos de aprendizaje no supervisado

Los algoritmos de aprendizaje no supervisado se utilizan cuando no se sabe a priori cuál es la salida deseada o correcta del sistema para un conjunto de datos de entrada dado. Son muy útiles cuando se tienen datos no etiquetados y se desea explorar su estructura para extraer información significativa. De acuerdo con Raschka y Mirjalili (2017, p. 7) esta información se obtiene sin la guía de una variable de salida conocida, propia de los algoritmos supervisados, ni con alguna función de recompensa como en el caso de los algoritmos de reforzamiento. Por otra parte, Paluszek y Thomas (2019, p. 4) plantean que el aprendizaje no supervisado no requiere datos de entrenamiento, y “se utilizan para descubrir patrones en datos para los cuales no hay una respuesta ‘correcta’.”

Los algoritmos de aprendizaje no supervisado por lo general caen dentro de dos categorías: algoritmos para agrupamiento (clustering) y algoritmos para reducción de la dimensionalidad. Ejemplos de estos tipos de algoritmos son: análisis de componentes principales, agrupamiento K-Means, agrupamiento DBSCAN y agrupamiento jerárquico.

Algoritmos de aprendizaje reforzado

En este tipo de aprendizaje el objetivo es desarrollar un sistema o agente que mejore su desempeño basado en las interacciones con el medio ambiente. En este caso, no hay un “maestro” que vaya indicando qué tan lejos o cerca se encuentra el sistema de la meta propuesta. El desempeño del sistema estará íntimamente ligado a la maximización de una “recompensa” a largo plazo.

Según Raschka y Mirjalili (2017, p. 6):

un ejemplo popular de aprendizaje reforzado es un ‘motor de ajedrez’. En este caso el agente decide una serie de movimientos dependiendo del estado en que se encuentre el tablero (el medio ambiente), y la recompensa se puede definir como ganar o perder al final del juego.

En la presente investigación, no se hace uso de algoritmos de aprendizaje reforzado.

Técnicas de detección de datos atípicos

Entre las técnicas de pre-procesamiento que se aplican a los datos previo al uso de los algoritmos de Machine Learning se encuentran: detección de datos faltantes, detección de datos duplicados, y detección de datos atípicos. Para los dos primeros casos la mayoría de los softwares utilizados para el análisis de datos tienen comandos para llevar a cabo la respectiva tarea de manera directa, pero para la detección de datos atípicos por lo general habrá que implementar alguno de los criterios existentes para tal fin. La detección y corrección de estas tres posibles “anomalías” en los datos es fundamental para que los modelos que se generen de la aplicación de los algoritmos de Machine Learning tengan suficiente validez estadística.

Un dato atípico, también conocido como “outlier”, es aquel que pertenece a un conjunto de datos particular, pero que esta considerablemente alejado del rango en el que se encuentran la mayoría de los datos del conjunto. Walpole et al. (2012 p. 24) definen los datos atípicos como “observaciones que se consideran inusualmente alejadas de la masa de datos”. Los consideran como “eventos raros”, pues la probabilidad de encontrar una observación alejada de la masa de datos es baja. De igual manera indican que “existen muchas pruebas estadísticas para detectar este tipo de valores”, pero en esta investigación se utiliza la prueba de Tukey para la detección de datos atípicos, la cual utiliza el Diagrama de Caja y Bigotes (Box-Plot) ya que según Moreno (2012, p. 14) “Es extensamente usado en la detección de outliers, quizá el más utilizado y popular entre todos los métodos”.

Prueba de Tukey para la detección de datos atípicos

La prueba de Tukey consiste en la obtención del diagrama Box-Plot para visualizar gráficamente la presencia de datos atípicos. De acuerdo con Amón (2010), el diagrama utiliza cinco medidas descriptivas de los datos: el primer cuartil (Q1), la mediana (Q2), el tercer cuartil (Q3), el valor máximo, y el valor mínimo. Se forma un rectángulo o caja cuyos dos lados corresponde al primer y tercer cuartil, y que además se cumple que el 50 % de los datos están ubicados dentro de la caja. Adicionalmente, los brazos o “bigotes” están representados por los valores mínimo y máximo, y la mediana es la línea que atraviesa la caja.

Para diferenciar los datos atípicos del resto de los datos, se hace uso de los límites inferior y superior, los cuales se construyen a partir del rango intercuartil (IQR), que no es más que la diferencia entre el tercer cuartil y el primer cuartil. Los datos serán atípicos si son menores al límite inferior o si son mayores al límite superior. El límite inferior se obtiene al restar del primer cuartil k veces el rango intercuartil, mientras que el límite superior se obtiene al sumar al tercer cuartil k veces el rango intercuartil. Cuando k = 1,5 los límites se utilizan para detectar datos atípicos “leves”. Por otra parte, cuando k = 3 los límites se utilizan para detectar datos atípicos “graves”.

3. Metodología

La investigación realizada es de tipo cuantitativa-evaluativa. Los datos utilizados fueron tomados de la página web de la DGEyC (2022), y están compuestos por los valores de energía eléctrica mensual facturada, en kilovatios por hora (kWh), por tipo de cliente, durante el período 2010-2021. Los datos incluyen: Energía total, Energía residencial, Energía comercial, Energía oficial, Energía industrial, Energía otros usuarios o clientes, así como el número de usuarios por cada una de esas categorías de clientes. En la matriz de datos total cada fila corresponde a una observación, y cada observación está compuesta por el año, el mes, el valor de consumo total de energía, los valores de energía eléctrica facturada por cada tipo de usuario para ese mes y año, el número de usuarios totales, y los números de usuarios existentes por cada tipo de usuario, para ese mes y año. En la Tabla 1 se presenta un resumen de los datos estadísticos de energía (kWh) por tipo de usuario.

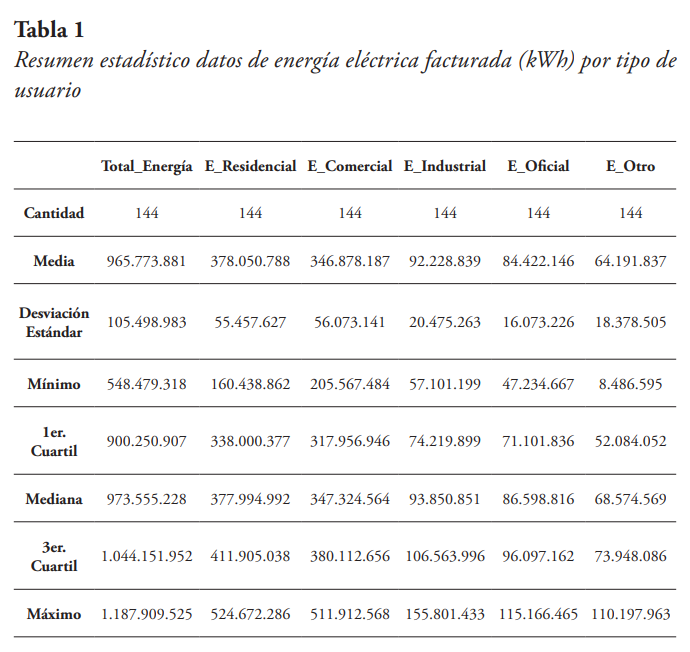
De la Tabla 1 se puede observar que hay un total de 144 datos correspondientes a la cantidad de meses existentes dentro del período de estudio. De igual manera se puede notar que los valores de la media y la mediana están cercanos entre sí, siendo su diferencia porcentual de solo 0,806 %, para el caso de la energía total. Siendo baja la diferencia porcentual para el resto de los tipos de energía, a excepción de la energía facturada de clientes oficiales con 2,58 %, y la energía facturada por otros clientes, cuya diferencia porcentual es de 6,83 %.

Seguidamente, se genera una matriz de coeficientes de correlación para determinar el nivel de correlación entre cada par de variables; la matriz resultante se muestra en la Figura 1.

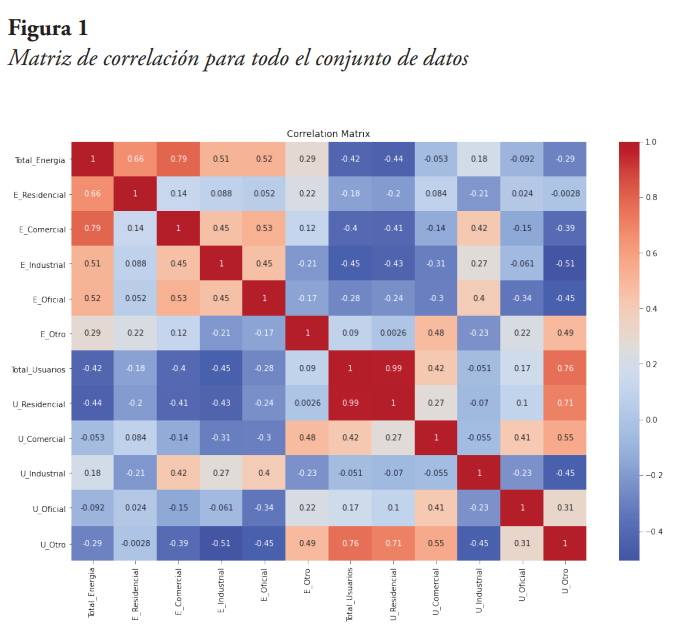
En la esquina superior izquierda de la matriz se pueden ver los valores de correlación entre cada par de variables de energía facturada, de lo cual se nota, como era de esperarse, que todas las energías facturadas de cada categoría de usuario tienen un valor positivo y mayor a 0,5 (a excepción del tipo de usuario Otro), con respecto a la energía facturada total. Resalta la energía facturada comercial con un coeficiente de correlación de 0,79 con la energía total facturada. De igual forma, se observa que la energía facturada residencial tiene un coeficiente de 0,66 con respecto a la energía total. Por su parte, la energía facturada de usuarios tipo “Otro”, tiene un coeficiente de correlación de solo 0,29 con la energía eléctrica total facturada.

En cuanto al número de usuarios, la mayoría de las categorías tiene un coeficiente de correlación negativo, y menor a 0,5 con respecto a la energía eléctrica total facturada, a excepción del número de usuarios industriales, que tiene un coeficiente positivo, pero menor a 0,5. Si se comparan los coeficientes de correlación de las categorías de usuarios entre sí, se puede ver que el número de usuarios residenciales tiene un coeficiente de correlación positivo y casi uno (0,99) con los usuarios totales; mientras que el número de usuarios “Otros” tiene un coeficiente de 0,76 con los usuarios totales.

Análisis inicial de los datos de energía eléctrica facturada

El análisis y procesamiento de los datos se realizó utilizando la herramienta Jupyter de Anaconda y código Python. Se hizo una revisión preliminar del conjunto de datos para determinar la posible existencia de datos faltantes, datos repetidos, datos atípicos, y verificar que los tipos de datos fuesen los correctos. En cuanto a la posibilidad de datos faltantes y/o repetidos, la verificación se realizó utilizando los comandos de código previstos para ello, de lo cual se concluyó que no hay datos faltantes ni repetidos.

Posteriormente, se hizo el análisis para la posible detección de datos atípicos, utilizando herramientas gráficas como diagramas Box-Plot e Histogramas. Se graficaron los Box-Plot de energía facturada de cada tipo de cliente para determinar la existencia de este tipo de datos, tal como se muestra en la Figura 2.

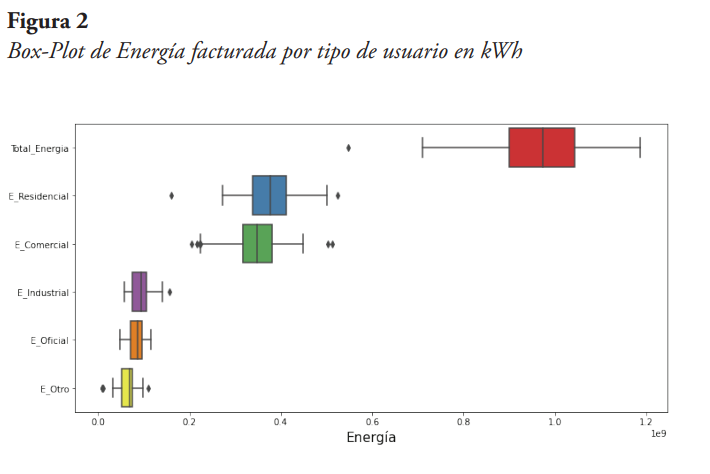
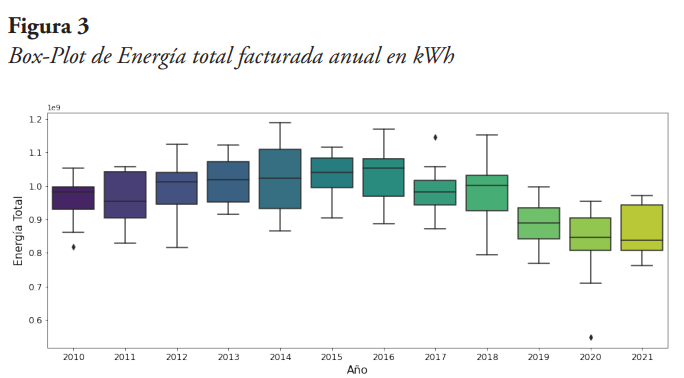
De la Figura 2 se puede observar que la energía total presenta un dato atípico significativo. De igual manera, se observa que este dato lo pudiera suministrar la energía residencial y/o la energía comercial. En la Figura 3 se tiene el Box-Plot por año, donde se observa que hay un dato atípico significativo en el año 2020, y dos datos atípicos adicionales, aunque no tan significativos, en los años 2010 y 2017.

La Figura 4 muestra el Box-Plot de la energía total por mes, del cual se observan datos atípicos para los meses de junio y agosto, siendo más significativo el ocurrido durante el mes de junio.

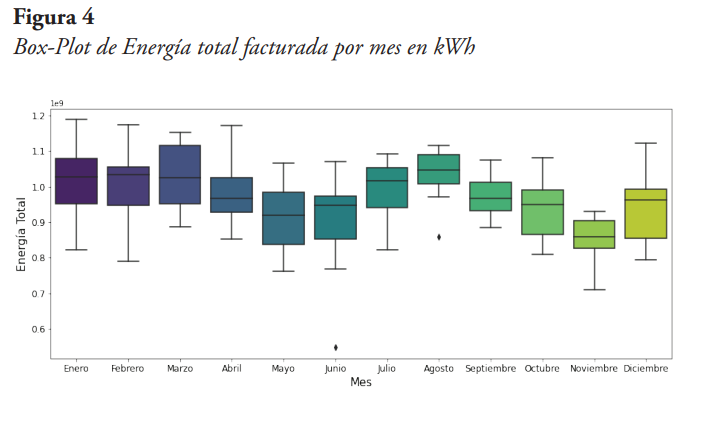
Ahora, aplicando la técnica del diagrama de caja y bigote para datos atípicos “leves” y datos atípicos “graves”, a los datos de energía total, se determinó que existen un dato atípico leve en el mes de junio del año 2020, justo cuando en la Ciudad de Buenos Aires se aplicaba una cuarentena estricta debido a la pandemia.

En cuanto a los datos de energía residencial, se consiguieron dos datos atípicos, uno para el mes de agosto del año 2018, y otro para el mes de junio del año 2020. Este último coincidiendo con los datos de energía total. Para el caso de energía facturada de clientes comerciales, se encontraron seis datos atípicos “leves”: cuatro en el año 2020, en los meses de junio, julio, octubre y noviembre; uno en el mes de diciembre 2012, y el otro en diciembre del 2013. Para el caso industrial, se consiguió un dato atípico “leve” en el mes de abril del año 2016. Finalmente, para los datos de energía facturada de clientes oficiales no se consiguieron datos atípicos, mientras que para clientes en la categoría “Otro”, se encontraron datos atípicos para el año 2011. Cabe destacar, que en ningún caso se encontró datos atípicos “graves”.

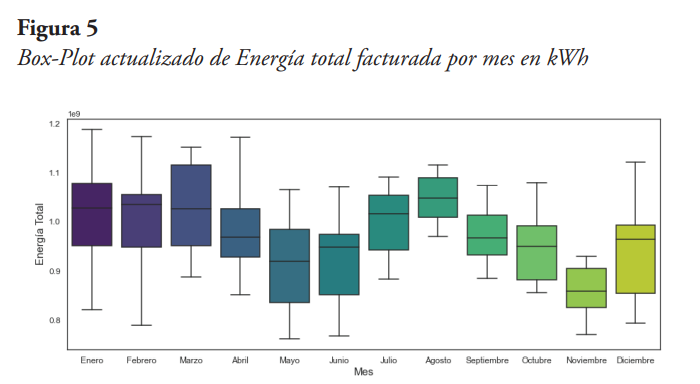
Se optó por imputar los datos atípicos, de los tipos de clientes residencial y comercial, con el promedio de los valores del mismo mes, para los años anterior y posterior al del dato atípico. El resultado obtenido se observa en el Box-Plot de la energía total por mes de la Figura 5, de la cual se nota que ya no existen datos atípicos para los datos de energía total facturada.

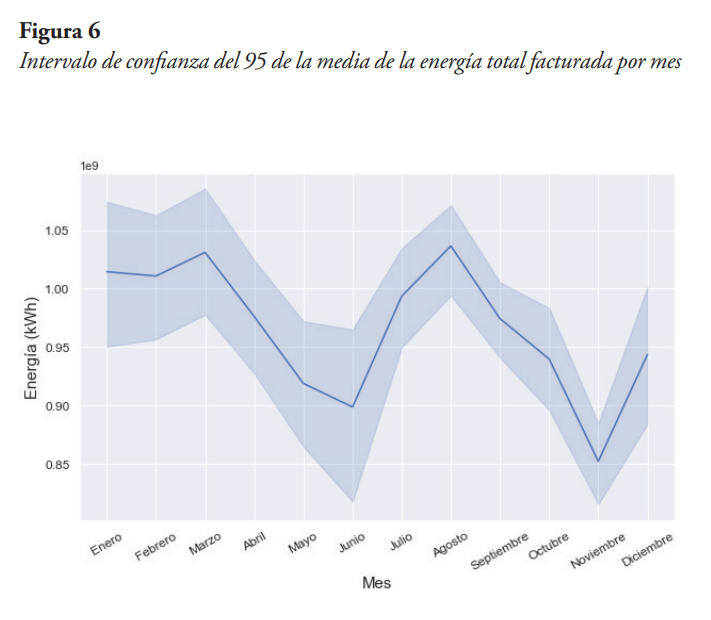
Finalmente, podemos ver el comportamiento de la energía eléctrica facturada total, graficando la media mensual en un intervalo de confianza del 95 %. Esta información se presenta en la Figura 6, de la cual se ve que, durante los meses de junio y noviembre, la energía facturada promedio tiene valores mínimos, mientras que en los meses de marzo y agosto ocurren los valores máximos.

Análisis inicial de los datos de número de usuarios

Aunque el número de usuarios por tipo de cliente forma parte del mismo conjunto de datos, se optó por desarrollar el análisis de datos atípicos de manera separada, al tener un comportamiento totalmente diferente con respecto a los datos de facturación de energía. Es así como en la Figura 7 se muestran los diagramas Box-Plot del número de usuarios por cada uno de los tipos de clientes.

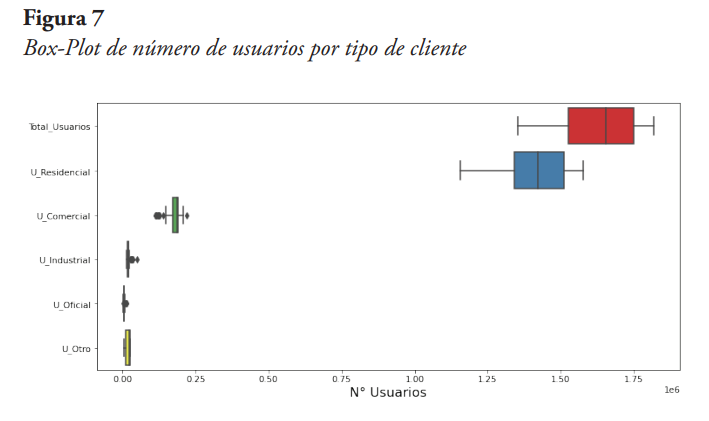
De esta Figura 7 se pueden deducir varias afirmaciones. Primero, el número total de usuarios está fuertemente definido por el número de usuarios residenciales, levemente definido por el número de usuarios comerciales, y casi nada por el resto de los tipos de usuarios. Segundo, se puede decir que para este conjunto de datos no se presentan valores atípicos, esto se verificó aplicando la técnica del diagrama de caja y bigote para datos atípicos “leves” y datos atípicos “graves”. Tercero, el número de usuarios comerciales, industriales, oficiales y otros han tenido muy poca variación durante el período de estudio.

Aplicación de los algoritmos de Machine Learning

Se aplicó el algoritmo de agrupamiento K-Means para identificar patrones dentro del conjunto de datos de energía eléctrica facturada. El número de clúster K se definió aplicando el “método del codo” para así obtener el valor óptimo. El otro algoritmo aplicado, del tipo de aprendizaje no supervisado, fue el análisis de componentes principales, que permitió identificar las variables del conjunto de datos que mejor explican la varianza del sistema.

De igual forma, se aplicó algoritmo de regresión lineal múltiple para obtener un modelo que permite predecir la energía eléctrica total facturada, y a la vez determinar cuáles variables tienen un mayor impacto sobre esa energía facturada. Se usaron los resultados del análisis de componentes principales como complemento para reducir la cantidad de variables explicativas del modelo.

4. Resultados obtenidos

Veremos a continuación, los resultados obtenidos luego de la aplicación de algoritmos de aprendizaje supervisado y no supervisado a los datos de energía eléctrica facturada mensual, y número de usuarios mensuales por tipo de usuarios.

Aplicación del algoritmo K-Means

El algoritmo K-Means es utilizado para agrupamiento o clustering, el cual, de acuerdo con Igual y Seguí (2017, p. 116),

es el proceso de agrupar objetos similares juntos entre sí; es decir, crear subconjuntos de grupos con tal que los objetos en un mismo grupo (clúster) sean similares entre sí y los objetos ubicados en grupos diferentes tengan características diferentes entre sí.

Se habla entonces de alta semejanza intraclase, y baja semejanza interclases.

El algoritmo inicia con el establecimiento manual del número de grupos (clústeres) K. Luego, según lo indicado por Russano y Ferreira (2020, p. 246),

a través de la iteración, el algoritmo asigna cada punto de datos a uno de los grupos en función de su posición en el espacio n-dimensional (1D, 2D, etc.). El agrupamiento se realiza según la similitud de los datos, es decir, los datos similares se unen bajo el mismo grupo. La similitud puede medirse con diferentes criterios, dependiendo del problema.

Después del proceso de iteración, el algoritmo entrega el centroide de cada clúster, utilizados para etiquetar cada dato del conjunto, así como a los nuevos datos, y etiquetas para los datos de entrenamiento del modelo.

Una de las desventajas de utilizar este algoritmo para hacer agrupamiento de datos, radica en el hecho de que el usuario define previamente el número de clústeres K. Sin embargo, tal como lo indican Umargono et al. (2020), se puede utilizar una metodología para obtener el valor óptimo de K. Esta se conoce como el “método del codo”, para lo cual debe definirse una métrica de optimización. Swamynathan (2017, p. 199) indica que el método del codo “consiste en aplicar el algoritmo K-Means para un rango de valores de K y calcular la suma de los errores al cuadrado o el porcentaje de varianza explicada, para cada valor de K.”

Para el caso analizado en esta investigación, se aplicó el algoritmo a todo el conjunto de datos. Dado que este algoritmo se basa en minimizar la distancia entre puntos del conjunto de datos, previo a su aplicación se normalizaron los datos.

Obtención del valor óptimo de K

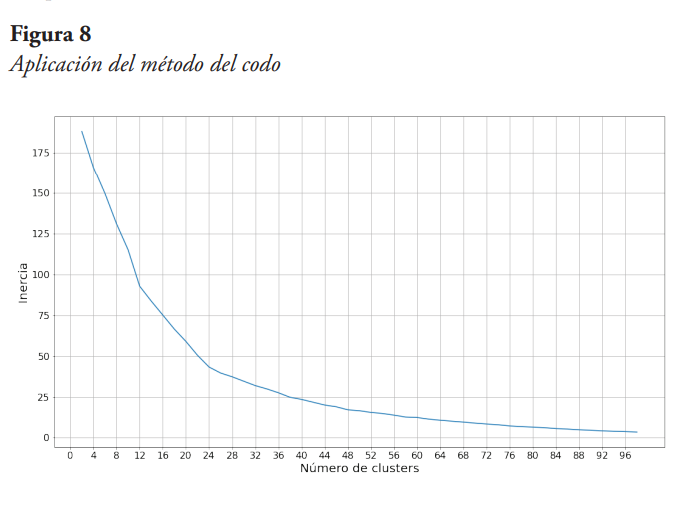
Para obtener el K óptimo se empleó el método del codo, utilizando como métrica la inercia, la cual es la función de costo de los clústeres, y consiste en minimizar la sumatoria de los cuadrados de la diferencia de cada punto al centro del clúster al que pertenecen. Los resultados obtenidos se presentan en la Figura 8, de la cual se observa que el valor de K para el cual la curva cambia su pendiente de manera más pronunciada es 12, por lo tanto, ese es el valor de K utilizado.

Obtención de los clústeres

Se utiliza entonces K=12, y se aplica el algoritmo. En la Tabla 2 se presenta el número de elementos de cada uno de los clústeres obtenidos, observándose que todos tienen el mismo tamaño y es igual a 12, y al ser 12 los clústeres, da el valor total de datos 144.

Es importante observar que en algunas ocasiones las variables categóricas del conjunto de datos podrían coincidir con los grupos o clústeres que se derivan de la aplicación del algoritmo. En este caso, las variables categóricas son el año (12 en total) y el mes (12 en total).

Del análisis de los clústeres, considerando la etiqueta año, se obtuvo que dada clúster contiene un elemento de cada uno de los años del período de estudio, por lo cual se deduce que esa categoría no define los clusters del agrupamiento. Seguidamente, en la Figura 9, se presenta el conteo de elementos que componen cada clúster, pero esta vez con la etiqueta del mes para cada elemento.

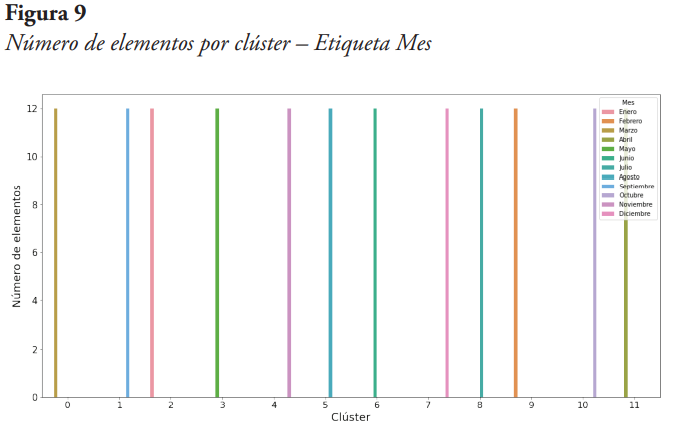
De la Figura 9 se puede notar que cada clúster tiene 12 elementos de un mismo mes. Por ejemplo, el clúster 0 está compuesto por los meses de marzo de los años que van desde el 2010 al 2021, el clúster 1 a los meses de septiembre del mismo período, el clúster 2 a los meses de enero, y así sucesivamente, por lo que se puede afirmar que los 12 clústeres obtenidos corresponden a los 12 meses del año. De lo anterior se puede inferir que los datos presentan una estacionalidad mensual, es decir, que el comportamiento de la energía eléctrica facturada está en cierta forma determinado por el mes del año en que se registra el consumo de esta energía.

Aplicación de algoritmo de análisis de componentes principales

El análisis de componentes principales (PCA) es una técnica que nos permite reducir la dimensionalidad de un caso de estudio, en términos de reducir la cantidad de variables que conforman un conjunto de datos, dejando solo las variables que tienen una mayor incidencia en la explicación de la varianza del sistema. PCA realmente transforma los datos originales en un nuevo conjunto de características con una dimensionalidad menor, este nuevo conjunto lo conforman las componentes principales, que se obtienen como una combinación lineal de las variables originales. La idea es que el nuevo conjunto de componentes tenga la mayor cantidad posible de información de los datos originales, y eso se mide con la proporción de varianza explicada por las componentes principales. Es una técnica muy utilizada para el preprocesado de predictores en el ajuste de modelos de aprendizaje supervisado.

En nuestro caso de estudio tenemos catorce variables, seis sobre energía eléctrica facturada, seis sobre cantidad de usuarios que consumen esa energía eléctrica, el mes del consumo, y el año del consumo. La aplicación de PCA, en este caso, es con el fin de seleccionar los predictores de la energía total facturada. Por tal razón, del conjunto de datos se extrae la energía total facturada antes de aplicar PCA.

En esta oportunidad, para generar el modelo PCA no se indica el número de componentes principales deseadas, de modo que por defecto será igual al menor valor entre el número de filas del conjunto de datos original menos uno y el número de columnas del mencionado conjunto. En este caso son 13 componentes principales, y la proporción de varianza que explica cada una de esas componentes, luego de aplicar la técnica, se muestra en la Figura 10.

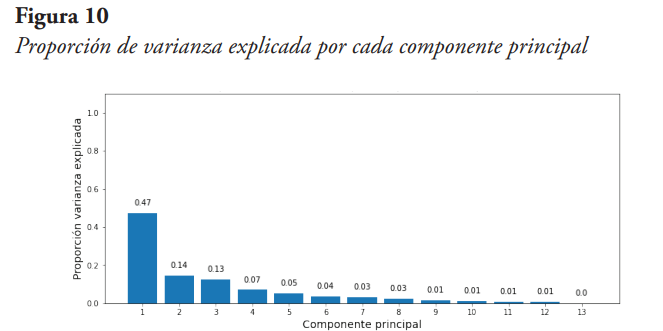
De la Figura 10 se puede observar que la primera componente principal ya explica un 47 % de la varianza, y el porcentaje que explica cada componente va disminuyendo a medida que se avanza en las componentes. De igual forma, se observa que la sumatoria de las varianzas explicadas de las 13 componentes es igual al 100 %, pero para efectos de reducir la dimensionalidad no tiene sentido escoger todas las componentes, pues es el mismo número de variables originales consideradas. Entonces, se debe definir un criterio para así hacer la reducción correspondiente. Para efectos de la reducción de dimensionalidad, se define como criterio seleccionar las componentes principales que en su conjunto explican al menos el 90 % de la varianza. Para ello obtenemos un gráfico de varianza explicada acumulada, el cual se presenta en la Figura 11.

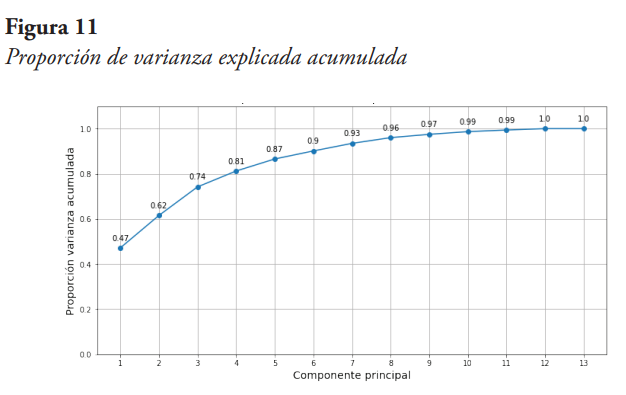
De la Figura 11 se puede observar, que con seis componentes principales ya se explica el 90 % de la varianza, por lo tanto, se seleccionan las seis primeras componentes principales (PC). Ahora, recordando que cada componente principal es la combinación lineal de las variables originales, en la Tabla 3 se presenta una matriz de pesos que relacionan cada componente principal con cada variable original, para las seis primeras componentes seleccionadas.

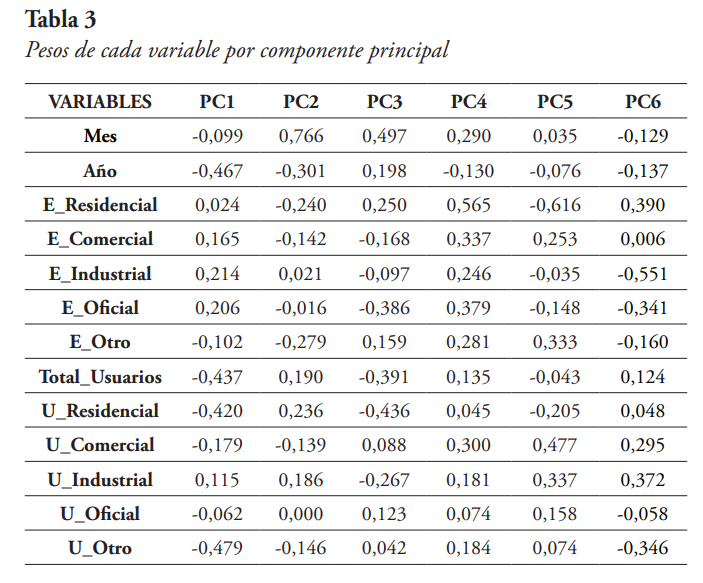
Obsérvese que la magnitud de los pesos varía entre 0 y 1. Mientras más cerca de 1, mayor influencia tendrá la variable original sobre la componente principal respectiva. Por el contrario, mientras más cerca esté de 0, menos significativa será la variable sobre la componente principal. De la Tabla 3 también se puede observar que las variables E_Comercial, E_Oficial, E_Otro, U_Industrial, y U_Oficial, tienen pesos bajos (por debajo de 0,4 en magnitud) en cada una de las componentes, por lo que pudieran ser descartadas en el posible diseño de un modelo de regresión, pues su impacto no es significativo desde el punto de vista de las componentes principales.

Aplicación del algoritmo de Regresión Lineal Múltiple

Este algoritmo consiste en generar un modelo de regresión en el que se quiere predecir una variable objetivo a partir de un conjunto de otras variables (explicativas). Para este caso, como variable objetivo se selecciona facturación total de energía eléctrica en la Ciudad de Buenos Aires, y como variables explicativas se tienen inicialmente las restantes trece variables del conjunto de datos. Sin embargo, se hace un análisis previo para determinar cuáles de esas posibles trece variables explicativas se podrían descartar del modelo.

Análisis de Correlación

Se calculó el coeficiente de correlación de cada una de las variables explicativas con la variable objetivo. Esto se realizó utilizando el método de Pearson, el de Spearman y el de Kendall. Los valores absolutos de los coeficientes de correlación obtenidos, ordenados de mayor a menor, se presentan en la Tabla 4, a continuación.

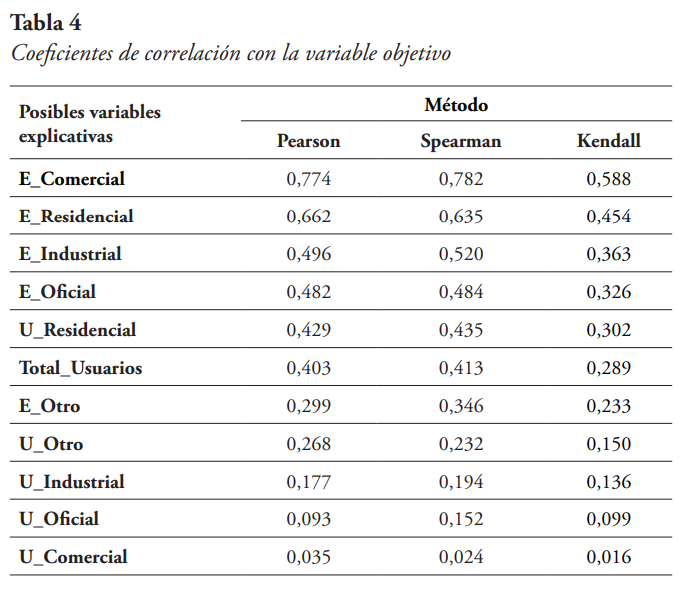
Se puede observar que para cada uno de los métodos utilizados el orden se mantiene igual, siendo la Energía Comercial la variable explicativa con mayor coeficiente con la variable objetivo, seguida por la Energía Residencial, la Energía Industrial y la Energía Oficial. Es importante resaltar, que el número de usuarios residenciales y el número total de usuarios tienen mayor coeficiente de correlación con la variable objetivo que la energía de otros usuarios (E_Otro). También se puede observar que el número de usuarios industriales, el número de usuarios oficiales y el número de usuarios comerciales tienen un coeficiente de correlación casi nulo con la variable objetivo.

Ahora, se espera que las variables explicativas además de tener un coeficiente de correlación relativamente alto con la variable objetivo tengan un coeficiente relativamente bajo entre ellas. En ese sentido, se extrajo la variable objetivo y se calculó el coeficiente de correlación entre cada par de variables explicativas. En la Figura 12 se presenta la matriz de correlación obtenida.

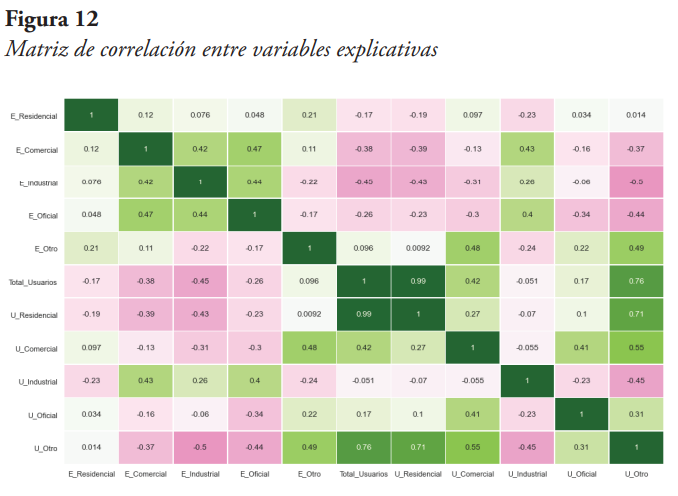
De la Figura 12 se puede observar que la variable Total_Usuarios tiene una alta correlación con U_Residencial (0,99) y con U_Otro, por lo que se elimina del conjunto de variables explicativas. Por otra parte, U_Otro tiene una alta correlación también con U_Residencial (0,71) y con U_Comercial (0,55), por lo que se elimina del conjunto de variables explicativas. De igual manera, se debe recordar que U_Industrial, U_Oficial, y U_Comercial tiene un coeficiente de correlación prácticamente nulo con la variable objetivo, por lo que también se eliminan del conjunto de variables explicativas.

Finalmente, haciendo uso de los resultados PCA se podrían eliminar las variables explicativas E_Oficial y E_Otro, ya que además sus coeficientes de correlación con la variable objetivo son relativamente bajos.

Obtención del modelo de Regresión Lineal

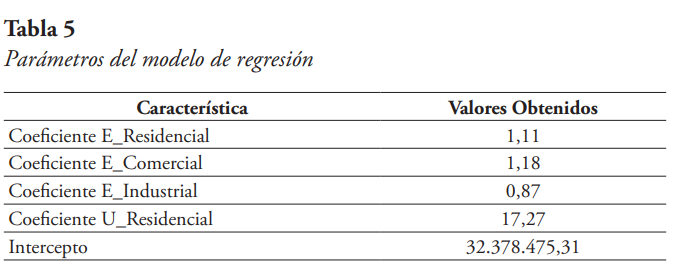
Entonces, para el modelo de Regresión Lineal Múltiple, se tienen como variables explicativas: la facturación de energía residencial (E_residencial), la facturación de energía comercial (E_Comercial), la facturación de energía industrial (E_Industrial) y el número de usuarios residenciales (U_Residencial). Cómo ya se mencionó, la variable objetivo es la facturación total de energía eléctrica.

El modelo se entrenó con el 75 % de los datos, y el 25 % restante se utiliza para la evaluación de este. El intercepto y los coeficientes obtenidos se presentan en la Tabla 5 siguiente, de la cual se puede decir que, al haber un aumento unitario del consumo de energía residencial, la variable objetivo aumenta 1,11 kWh. De igual manera, al haber un aumento unitario en el consumo de energía comercial, la energía total facturada aumenta 1,18 kWh, y en el caso de la energía industrial el aumento sería de 0,87 kWh. En cuanto al número de usuarios residenciales, al haber un aumento unitario, el modelo indica que la energía total facturada mensual aumentaría 17,27 kWh.

Evaluación del modelo

El restante 25 % de los datos se utilizó para obtener predicciones y así poder evaluar el modelo. Uno de los indicadores utilizados es el coeficiente de determinación R², que según Walpole (2012, p. 407) “es una medida de la calidad de ajuste del modelo, y muestra la proporción de la variabilidad explicada por el modelo ajustado”. Es un indicador que varía entre 0 y 1, valdrá 1 cuando el ajuste del modelo sea perfecto. Por el contrario, un valor cercano a 0 indica un ajuste deficiente del modelo. Por lo tanto, lo que se busca es que este indicador este lo más cercano posible a la unidad.

Los otros dos indicadores utilizados son la raíz cuadrada de la media de los errores al cuadrado (RMSE), y la media del valor absoluto de los errores (MAE). En ambos casos, las unidades son las mismas de la variable objetivo, es decir kilowatt-hora (kWh). El error o residuo no es más que la diferencia entre el valor real y la predicción respectiva. Por otra parte, se aplicó la prueba de Shapiro-Wilk para contrastar la normalidad de los residuos. La hipótesis nula es que los residuos provienen de una población normalmente distribuida, y el estadístico utilizado varía entre 0 y 1. Si el p-valor es mayor al nivel de significancia (por lo general 5 %) se concluye que no se puede rechazar la hipótesis nula. En la Tabla 6 se presentan los resultados de la evaluación.

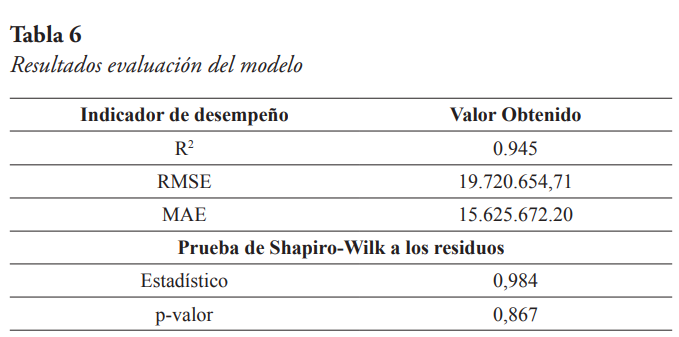
De los resultados de la evaluación del modelo se puede observar que el R² es cercano a uno, lo cual es indicativo de un buen ajuste del modelo. Adicionalmente, se puede notar que no se rechaza la hipótesis de que los residuos provienen de una población normalmente distribuida. En cuanto al RMSE, este tiene un valor de algo más de 19 millones de kWh, y el MAE un valor de algo más de 15 millones de kWh. Estos dos valores son relativamente bajos si se comparan con la media de los datos de energía total facturada que es de aproximadamente 966 millones de kWh.

5. Conclusiones

Los datos de energía eléctrica facturada total presentan una estacionalidad mensual evidenciada por los clústers obtenidos luego de aplicar el algoritmo K-Means, el cual agrupó los datos de acuerdo con el mes en que se encontraban. Lo anterior confirma lo encontrado en el análisis inicial de los datos en el sentido de que, en promedio, se presenta una mayor facturación de la energía eléctrica total durante los meses de enero, febrero, y marzo. Mientras que, en los meses de mayo, junio y noviembre la facturación es menor. De igual manera coincide con lo establecido en MINEM (2016) sobre la estacionalidad de la demanda.

El número total de usuarios que consumen energía eléctrica en la Ciudad de Buenos Aires está altamente influenciado por el número de usuarios residenciales, con un aumento del año 2011 al 2012, luego una caída hasta el año 2013, donde prácticamente se mantuvo hasta el 2015, y a partir del cual experimentó un aumento sostenido hasta el 2018. A partir de este último año las variaciones han sido mínimas.

De acuerdo con el modelo de regresión lineal se puede establecer que la energía eléctrica facturada para los usuarios comerciales, residenciales e industriales, así como el número de usuarios residenciales son las variables (del conjunto de datos original) que mayor impacto tienen sobre la energía eléctrica facturada total en la Ciudad de Buenos Aires para el período 2010-2021. Lo anterior coincide con MINEM (2016) en lo que respecta a la influencia de los clientes residenciales sobre la demanda total de energía. Este modelo de regresión presenta un buen desempeño, con un R² cercano a la unidad y un error absoluto medio que solo alcanza el 1,62 % del valor medio de la energía total facturada.

El análisis de componentes principales nos permitió reducir la dimensionalidad del conjunto de datos, previo a la aplicación del modelo de regresión lineal. Con las seis primeras componentes principales ya se explicaba el 90 % de la varianza del sistema, por lo que las variables del conjunto de datos que eran significativas solo en las seis restantes componentes fueron eliminadas del conjunto de posibles variables explicativas de la energía total facturada.