Diseño mecánico de palas para un aerogenerador de 250w de potencia

Introducción

La energía eólica es una fuente de energía renovable que ha experimentado un enorme crecimiento en las últimas décadas (Cooperman, Eberle, & Lantz, 2021). Los aerogeneradores de baja potencia trabajan bajo el principio de transformar la energía cinética de un recurso eólico en trabajo mecánico, que a su vez logra convertir esa energía mecánica en energía eléctrica a través de un generador (Junginger, Hittinger, Williams, & Wiser, 2019). Debido a las condiciones climáticas que se presentan en la República Dominicana, la Comisión Nacional de Energía (CNE) establece que en el territorio nacional se tienen condiciones climáticas adecuadas para producir energía.

Las condiciones que presentan las áreas rurales son ideales para esta clase de proyectos, y en los estudios realizados en otras naciones se ve un impacto positivo dentro de este tipo de comunidades (Ngbara Touafio, Sanda, Malenguinza, M’Boliguipa, & Mouangue, 2020).

Para una buena generación dentro de un área determinada se necesita una combinación de características de vientos que favorezcan la producción de energía (Saint-Drenan et al., 2020). Estos factores pueden ser desde la velocidad del viento promedio dentro de un determinado periodo de tiempo, los patrones de viento estacionales, entre otros (López-Villalobos, Rodríguez-Hernández, Martínez-Alvarado, & Hernández-Yepes, 2021). En general, las ubicaciones con una velocidad media anual del viento de 7 m/s o más son las más adecuadas para los sistemas de energía eólica conectados a la red de servicios públicos. Las aplicaciones de energía rural son usualmente viables a velocidades de viento más bajas (5 a 6 m/s), en algunos casos a velocidades de viento tan bajas como 4.5 m/s (Elliott et al., 2001).

El diseño de aerogeneradores pequeños representa una solución efectiva y económica en las regiones del caribe (Costoya, de Castro, Santos, Sousa, & Gómez-Gesteira, 2019). Es por lo que este documento se enfoca en el diseño mecánico de las palas aerogeneradores de eje horizontal (HAWT – Horizontal Axis Wind Turbine en inglés) con una capacidad de generación de 250 W y su impacto en el medio ambiente.

Metodología

La estructuración de este artículo se basa en la presentación gradual de los conocimientos y deducciones basada en los datos arrojados mediante la investigación, empleando la metodología que se describe a continuación:

• Planteamiento para diseño y selección de los componentes mecánicos para palas mecánicas de aerogenerador de baja potencia de eje horizontal de 250 W
• Búsqueda exhaustiva basada en palabras clave en distintas bases de datos como ScienceDirect e IEEE Xplore. La delimitación de palabras fue una combinación de las siguientes palabras: Energía eólica; Palas de aerogenerador; SolidWorks; Aerogenerador; HAWT.
• Filtrado de información: se realizó mediante una serie de pautas correspondientes a trabajos de investigación, trabajos de revisión, actas de congresos y libros de textos.
• Análisis y simulación de datos: se realizaron las simulaciones pertinentes, expuestas en el documento, utilizando softwares computacionales.

Dimensionamiento del aerogenerador

Descripción del sistema global

La conformación de un aerogenerador está basada en la unión de una serie de elementos con la finalidad de poder convertir la energía mecánica en energía eléctrica aprovechando el viento, para luego poder alimentar las cargas (Xi et al., 2020).

Las principales partes de un aerogenerador incluyen los siguientes componentes:

• Rotor: pieza que gira de manera continua dentro de una máquina eléctrica, (generadores o motores eléctricos), encontrándose ubicada en su contraparte, el estator (Sugathapala, Boteju, Withanage, & Wijewardane, 2020).
• El movimiento mecánico transferido por el viento es llevado hasta el generador gracias al eje de transmisión, que acopla la turbina al rotor del generador (Rauert, Herrmann, Dalhoff, & Sander, 2016).
• Soporte o torre: estructura tubular que soportar la góndola y el rotor (Mühle, Adaramola, & Sætran, 2017).
• La potencia eléctrica generada, es distribuida mediante un cableado y un circuito eléctrico que trasporta la energía desde su punto de generación hasta un banco de baterías, donde se almacena para su uso posterior (Rommel, Di Maio, & Tinga, 2020).
• Las palas mecánicas o también conocidas como aspas de aerogeneradores es el componente encargado de recolectar la energía del viento (Denhof, Staar, Lütjen, & Freitag, 2019). El diseño determina la cantidad de energía que se recolectará del viento (Moghadassian & Sharma, 2020). Con el tiempo estas han ido mejorando la eficiencia, y la reducción de fricción con el eje (Micha, Mohan, & Sivamani, 2017).
• En el mercado se encuentran una variedad de aerogeneradores de distintos tipos como los de eje vertical (Li, Maeda, Kamada, & Mori, 2017), los de sistema de direccionamiento por veleta (Alsailani, Montazeri, & Rezaeiha, 2021), con el empleo de distintos materiales dependiendo del área de utilización (Gugliani, Sarkar, Ley, & Matsagar, 2021). Esta investigación se enfoca en la construcción de palas para aerogeneradores de eje horizontal con una potencia de 250 W.

Dimensionado del modelo propuesto

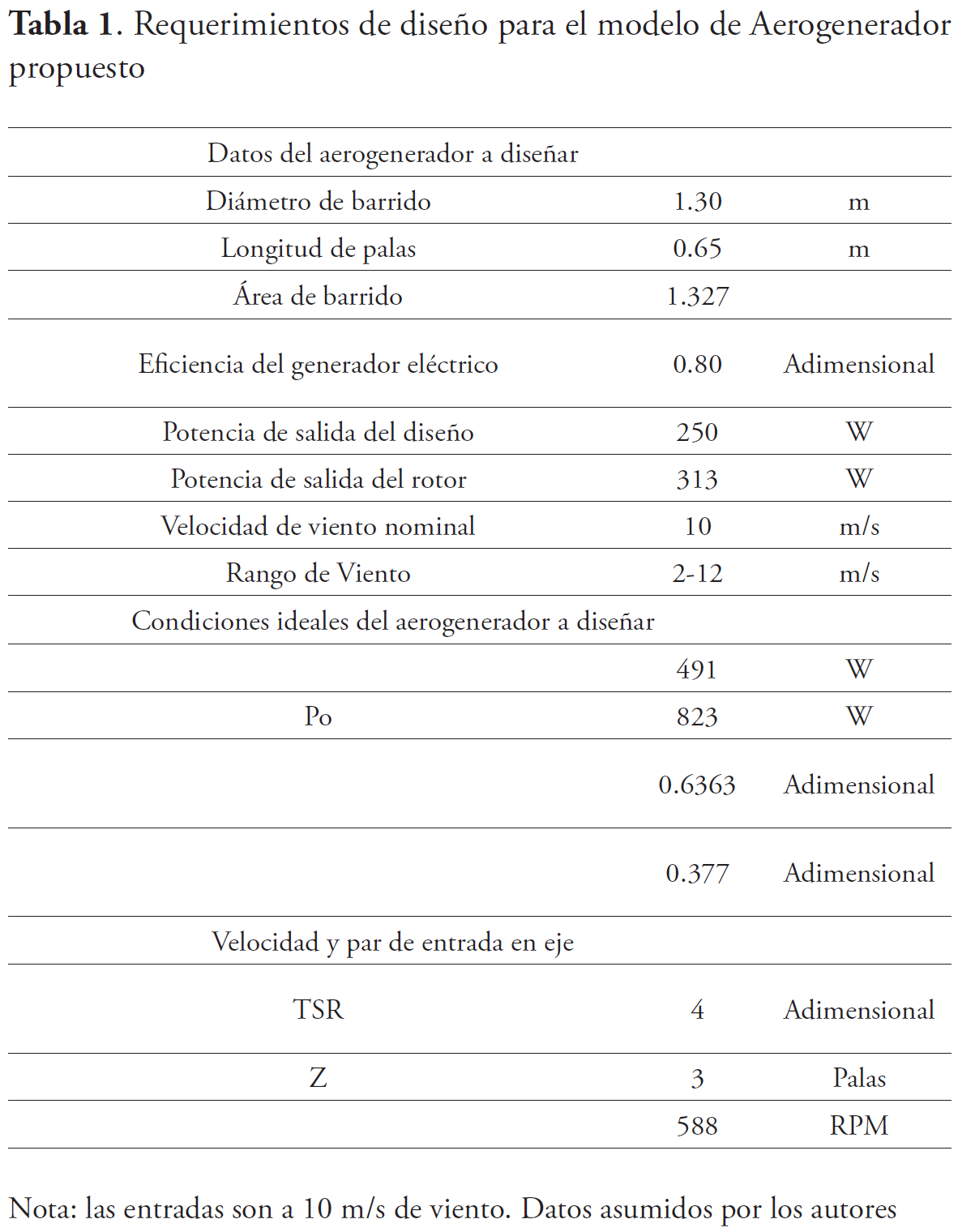
El rotor del aerogenerador posee un diámetro de barrido de 1.30 m, equivalente a 0.65 m (65 mm) de longitud para cada una de las 3 palas. Se toma para condiciones estándares una eficiencia del generador eléctrico del 80 % (Lara, Merino, Pavez, & Tapia, 2011). La potencia ideal para la entrega es de 250 W por las condiciones de viento que se presenta en estas zonas (Garcia et al., 2019), esto es posible determinar gracias a una serie de modelados o sistemas de predicción de vientos dentro de un periodo de tiempo (Dong, Li, Gao, & Zheng, 2020).

Para vientos de 10 m/s, con el tamaño de aerogenerador diseñado, solamente se puede extraer 491 W (tomando en cuenta el Límite de Betz), pero la energía total del viento en estas condiciones es de 823 W, la cual no es completamente disponible. Las palas están diseñadas con un TSR (Tip Speed Ratio) de 4, significando que la velocidad en la punta de las palas del rotor aumenta cuatro veces la velocidad del viento. A 10 m/s el rotor gira a 588 RPM.

Al relacionar la potencia requerida (313 W) con la potencia disponible a 10 m/s de viento (491 W), se determina un rendimiento de 63.63 % y un factor de potencia del aerogenerador de 37.7 %. Mientras más alto este factor, mejor eficiencia posee el aerogenerador. Sin embargo, existe un punto máximo para este factor, el cual depende mayormente del diseño de las palas. Mediante los cálculos de referencia del libro Introduction to Wind Turbine Aerodynamics (Schaffarczyk, 2014), se procuró que este factor sea alcanzado alrededor de los 10 m/s. Los demás componentes mecánicos, como el eje de transmisión, carcasa, veleta y torre son diseñados con base en las referencias de varios autores de otros modelos similares de aerogeneradores HAWT de baja potencia. Para el diseño del eje, se utiliza los procedimientos del libro de Diseño en Ingeniería Mecánica de Shigley, (Budynas & Nisbett, 2012). En la tabla 1 se presentan los requerimientos que se usaron para el diseño de las palas.

Diseño de partes mecánicas: rotor

Es el componente que sostiene las palas y las conecta al eje principal de la máquina eólica. Los rotores vienen en muchas formas y configuraciones diferentes, principalmente dependiendo del tipo de generador utilizado y del diseño de las palas del rotor (Bernuzzi et al., 2021).

Las tres palas diseñadas utilizan un perfil aerodinámico NACA 4412 (Schmitz, 2020), con un TSR igual a 4, basado en los datos obtenidos de la herramienta Airfoil Tools. En cuanto el procedimiento aplicado se referencia en el libro de Introducción a la teoría de turbinas eólicas (Voneschen, 2009) conocido como “Método de las palas óptimamente diseñadas”. El material es de madera Plywood debido a la disponibilidad local y su costo. El método para la fabricación de palas por costillas (Lima Menjívar, Orellana Ramos, & Valencia Gómez, 2017), persigue el objetivo de mejorar la técnica de fabricación de la pala, por lo que se describe un procedimiento que facilite la aplicación de esta técnica de fabricación:

1. Usar una plantilla que contenga los perfiles de distintos tamaños y orientaciones correspondientes de la pala. En la plantilla cada perfil estará en un cuadro dentro de la plancha de madera, contendrá un agujero central por el que será atravesada una varilla de metal con extremos roscados para el apriete y lograr la estabilidad de la estructura.

2. Cortar en la plancha de madera las plantillas con una impresora láser u otra herramienta de corte. En el corte sale el perfil con su agujero.

3. Apilar en orden de tamaño (mayor a menor) los perfiles cortados. Se pegan con pegamento epóxido e irán tomando la orientación diseñada, y al mismo tiempo se crea un molde de madera con los cuadros cortados de donde sale el perfil, que sirve como molde para los perfiles de las otras aspas.

4. Introducir varilla de metal con puntas roscadas a través de los agujeros de los perfiles dentro del molde de madera. Enroscar en ambos extremos con tornillos para asegurar el apriete entre perfiles. Finalmente, se retira la pala desde la parte de abajo del molde de madera fabricado.

5. Realizar un recubrimiento de fibra de vidrio para añadir mayor resistencia a las palas, así como suavizar las superficies para mayor aerodinámica.

Diseño de partes mecánicas: eje de transmisión

El eje conecta el rotor con un acoplamiento al generador eléctrico. De esta manera se transmite el torque generado en el rotor hasta el generador eléctrico. El material es acero 1020 CD, para el diseño del eje de transmisión fueron utilizandos los libros de Diseño en Ingeniería Mecánica de Shigley (Budynas & Nisbett, 2012) y Diseño de Maquinaria (Norton, 2009). Se hicieron los cálculos analíticos de cargas en el eje utilizando el software MD Solids.

Datos de entrada:

• Peso del Rotor (P1): 121 N
• Par de entrada = Par de salida: 5.00 Nm (para un viento de 10 m/s).
• Factor de Diseño (N_f): 1.5
• Material: Acero 1020 CD

En la figura 2 se presenta los valores usados para hacer los análisis de fuerza cortante y momento flector del eje de transmisión. En la figura 3 se presenta las longitudes evaluadas para obtener las concentraciones de esfuerzo en el eje. Las condiciones de carga en el eje se tomarán como constantes, debido a las características del viento como:

• Los cambios de velocidad del viento ocurren de manera gradual y no repentinamente. Por lo que si la velocidad del viento disminuye la inercia del rotor mantiene la rotación de las palas a una velocidad que desacelera a ritmo constante. En caso contrario, si la velocidad del viento aumenta, se diseñó en la condición máxima de torque establecido (10 m/s), por lo que cualquier otra velocidad no representará un peligro al eje diseñado.
• Las palas del aerogenerador están diseñadas para rotar en un solo sentido, garantizándose por el mecanismo de orientación que alinea el aerogenerador en la dirección del viento.

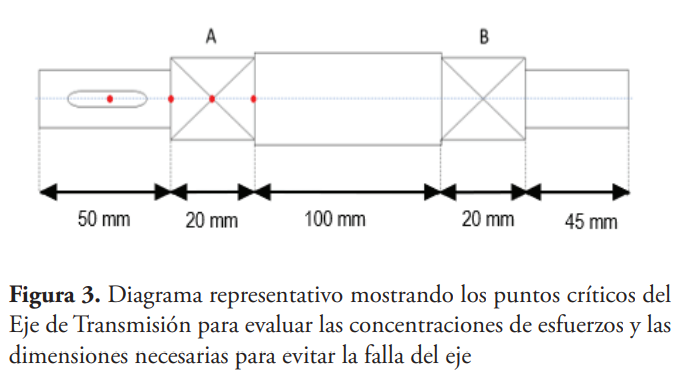
Se evalúa el Torque aplicado como un Torque Medio y el Momento Flector resultante como un Momento Alternante, donde el punto 2 es donde ocurre el Momento Flector Máximo en el eje. Usando la ecuación 6.8 del libro Diseño de Máquinas un enfoque integrado (Robert L Norton, 2011. pág. 422) se usó para determinar el diámetro requerido en el eje. Los escalones (cambios de sección), se tomaron con una relación típica de 1.20, es decir, la relación entre el diámetro superior y el diámetro inferior en el eje.

La ecuación (1), se obtiene cuando en la ecuación 6.8 del libro Diseño de Máquinas un enfoque integrado (Robert L Norton, 2011. pág. 422) Mm = Ta = 0 , se reduce a lo siguiente:

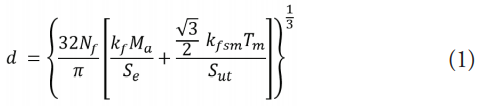
Análisis en el punto 2:

• Ma = 4235 N-mm
• Tm = 5000 N-mm
• N_f = 1.5
• Material: Acero 1020 CD

Los valores para k_fs (flexión) y k_fsm (torsión), se asumen inicialmente de manera conservadora como 1.7 y 1.5, respectivamente, para un filete de hombro bien redondeado (r/d = 0.1). El valor corregido de resistencia a la fatiga S_e, depende de diferentes constantes en base a las condiciones de trabajo

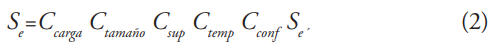
donde C_carga es el factor de carga, (Adimensional).

C_tamaño es el factor de tamaño, (Adimensional).

C_sup es el factor de superficie, (Adimensional).

C_temp es el factor de temperatura, (Adimensional).

C_conf es el factor de confiabilidad, (Adimensional).

S_e´ es el Limite de resistencia a la fatiga, (MPa o N/m$m^2$ ).

Para los aceros se cumple que, si la resistencia última del material S_ut es menor a 1400 MPa, entonces el Límite de resistencia a la fatiga es igual a 0.5S_ut (Ecuación 4.5a, Norton, 2009, p. 260). Entonces:

S_e´ = 0.5S_ut = 0.5(460) = 230 MPa.

Los factores de corrección se determinaron de la siguiente manera:

o Factor de Carga

Para casos de torsión pura o flexión, C_carga = 1.000

o Factor de Tamaño

El diámetro del eje a diseñar debe estar entre 2.79 y 51 mm (Ecuación 6.20, Budynas & Nisbett, 2012, p. 275). Tomando una estimación inicial del diámetro como 10 mm, el factor de tamaño es:

C_tamaño = 1.24$d^{-0.107}$ = 1.24(10)${}^{-0.107}$ = 0.9692

o Factor de Superficie

Para el acabo superficial de Maquinado o Laminado en frío.

C _sup = aS_ut${}^b$ = (4.51)(460)${}^{-0.265}$ = 0.8883

o Factor de Temperatura

La temperatura de trabajo puede asumirse como 50 º, tomando en cuenta el generador eléctrico. (Con la tabla 6-4, Budynas & Nisbett, 2012, p. 278).

C _temp = 1.008

o Factor de Confiabilidad

Con una confiablidad del 95 %, se utilizó la Tabla 6-5 (Budynas & Nisbett, 2012, p. 279).

C_conf = 0.868

Por tanto, el valor corregido de esfuerzo a la fatiga es tomado como:

S_e = C_carga*C_tamaño*C_sup*C_temp*C_conf*S_e´

S_e = (1.000)(0.9692)(0.8883)(1.008)(0.868)(230) = 173 MPa

Introduciendo los valores en la ecuación (1):

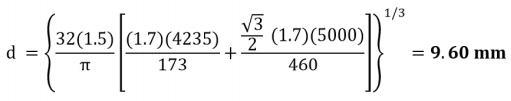
En la tabla A-17 p. 999 del libro de Budynas y Nisbett (2012) para las dimensiones estándar, el diámetro comercial del eje en su punto crítico es de 10 mm. Con una relación de escalones típico de 1.20, el diámetro siguiente es de 12.00 mm, y el anterior es de 9 mm. Las dimensiones en el otro extremo del eje serán las mismas determinadas para el punto crítico.

Después de confirmadas las dimensiones críticas, se seleccionó las dimensiones como 20 mm, 25 mm y 30 mm para los diámetros en los puntos 1, 3, 4, por razones de conveniencia para los cojinetes que se seleccionan con base en la Carga Nominal de Catálogo C_10., usando ecuación 11.3, de Budynas y Nisbett (2012, p. 551), para una confiabilidad del 90 %.

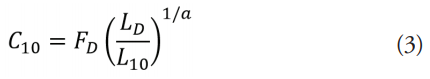
donde:

C₁₀ es la Carga Nominal de Catálogo, (Adimensional).

F_D es la Carga Real del cojinete, (Adimensional).

L_D es la vida útil de diseño, (Adimensional).

L₁₀ es la vida útil nominal, (Adimensional).

a es el parámetro del tipo de cojinete, (MPa o N/mm${}^2$).

Del software MDSolids, se obtuvieron las cargas reales en los cojinetes como las reacciones en los apoyos A y B, y sus magnitudes son 156 N y 35 N, respectivamente, seleccionando un solo tipo de cojinete con base en el apoyo A. Determinando la vida útil por

Donde:

n es la velocidad nominal del cojinete, (rev/min o RPM).

L_Des la vida útil de diseño en el tiempo, (horas).

Los libros establecen una vida útil en diez millones de revoluciones (${10}^6$). El parámetro para el tipo de cojinete es:

o a=3, para cojinete de bolas.

o a=10/3, para cojinete de rodillo o cónico.

Utilizando la tabla 11.4 (Budynas & Nisbett, 2012, p. 559), se toma en cuenta las horas de operación efectiva (a máxima capacidad) como 8 horas. Para máquinas para servicio de 8 h, establecemos una vida útil en tiempo de 10 000 horas. La velocidad nominal de los cojinetes es de 600 RPM. Introduciendo en la ecuación (c).

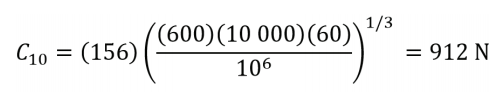
Comentarios

Los cojinetes de referencia, para un diámetro de 25 mm, tienen cargas nominales del orden de los kN, por lo que las necesidades de diseño están cubiertas en esta parte. Adicionalmente, los cojinetes poseen retenedores de aluminio para mantener la fijación del eje a pesar de las vibraciones y movimientos erráticos.

Diseño de partes mecánicas: otros componentes

CARCASA

Es el componente que protege los elementos, con suficiente espacio como para añadir elementos adicionales de control, posee dos partes, las cuales están unidas por dos bisagras y una cerradura de pestillos de palanca que evita que se abra durante operación.

VELETA

Es el dispositivo de orientación situado en la prolongación del eje del rotor. Están constituidas por una superficie plana metálica o de madera, sobre la que el viento ejerce una presión en el momento en que no están orientadas paralelamente en la dirección de este, provocando un par de giro que orienta la máquina (Gato, Maduro, Carrelhas, Henriques & Ferreira, 2021).

Se necesitan dos soportes: 1) El que une la carcasa con el tubo de dirección, 2) El que une el tubo de dirección con el soporte de veleta. Ambos implicarían el uso de maquinado y soldadura. La plancha de madera puede extraerse de las mismas que se usen para las palas.

TORRE

Consta de una base en forma de trípode atornilladas al suelo. Estas patas son soldadas a un tubo de acero, hueco, en el que se inserta otro tubo, igualmente hueco, dando la altura completa para la máquina eólica. En el extremo superior, se conecta un soporte giratorio (con cojinete), el cual permite la sujeción de la carcasa a la torre, así como la rotación de este.

Resultado de las simulaciones

ROTOR

• Cálculo de potencia y velocidad de giro

Con los parámetros especificados del aerogenerador, aplicamos las fórmulas para la potencia de salida y velocidad de giro en el rotor (Voneschen, 1989; 2009).

donde

P_w es la potencia entregada por el rotor, (W).

C_p es el factor de potencia del rotor, (Adimensional).

P_w,max es la potencia teórica máxima posible entregable por el rotor, (W).

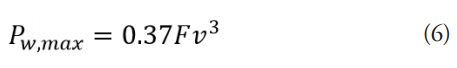
Donde:

F es el área de barrido por las palas, ($m^2$)

v es la velocidad del viento que atraviesan las palas, (m/s).

Donde:

λ es el Tip Speed Ratio (TSR), (Adimensional)

D es el diámetro de barrido de las palas, (m)

n el número de revoluciones por minuto a las que gira el rotor, (RPM)

En la tabla 2 se presenta los valores de velocidad del viento correlacionado con la velocidad angular del eje del rotor en revoluciones por minuto (RPM) y la potencia aproximada de salida de este para esas condiciones.

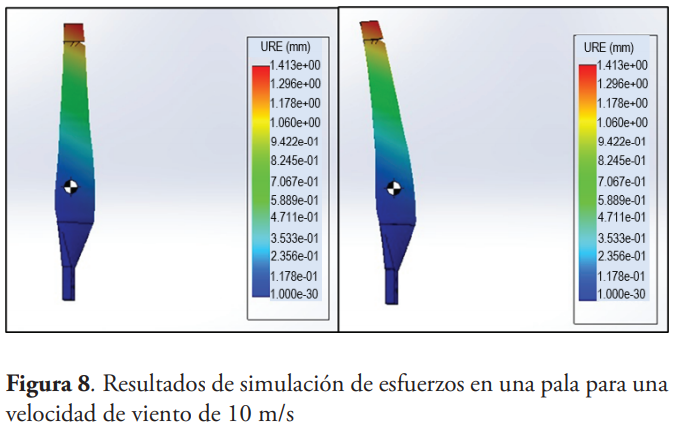
Cálculos de esfuerzo de flexión y visualización de resistencia al viento de las palas

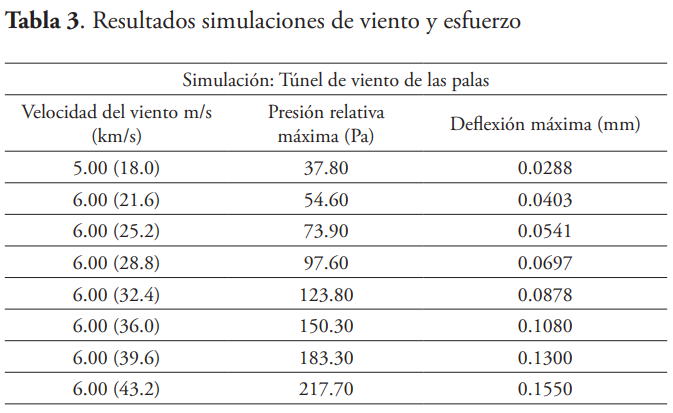
Se utilizaron las herramientas de Solidworks Flow Simulation para observar el comportamiento del viento en un rango de 5 a 12 m/s cuando atraviesa una pala. De esta simulación, se importaron los datos de los esfuerzos generados sobre la superficie de la pala y se determinó la deflexión máxima resultante en Solidworks Stress Analysis, cono se muestra en la tabla 3.

Comentarios

La deflexión de las palas es mínima por la acción del viento. Esto es debido al material seleccionado de madera Plywood, el cual es bastante rígido y resistente.

• Curva característica de las palas en función del TSR

Con el documento sobre Introducción a la teoría de las turbinas eólicas (Voneschen, 2009), es posible realizar los cálculos aproximados para determinar el factor de potencia de la pala dependiendo del TSR (figura 7). Los datos de los coeficientes de arrastre y sustentación para distintos ángulos de ataque del perfil NACA 4412 fueron extraídos de la página web de AirfoilTools (AirfoilTools, 2020). De acuerdo con la teoría de turbinas eólicas, el punto de la pala donde se estima el factor de potencia de la pala completa es en el 72 % de su longitud total, partiendo desde el centro del rotor (Voneschen, 2009). En la figura 5 se presenta la relación de velocidad de la punta (TSR) frente al coeficiente de potencia (CP) y tabla 4 se presenta los valores simulados para los coeficientes de las palas propuestas.

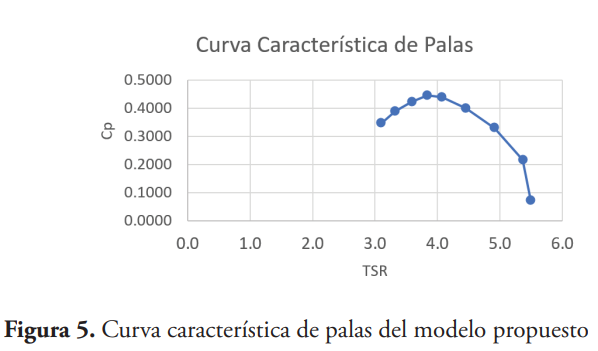
En la tabla 4 se puede observar que para los ángulos se obtienen un coeficiente de potencia mayor como se muestra a continuación:

TORRE

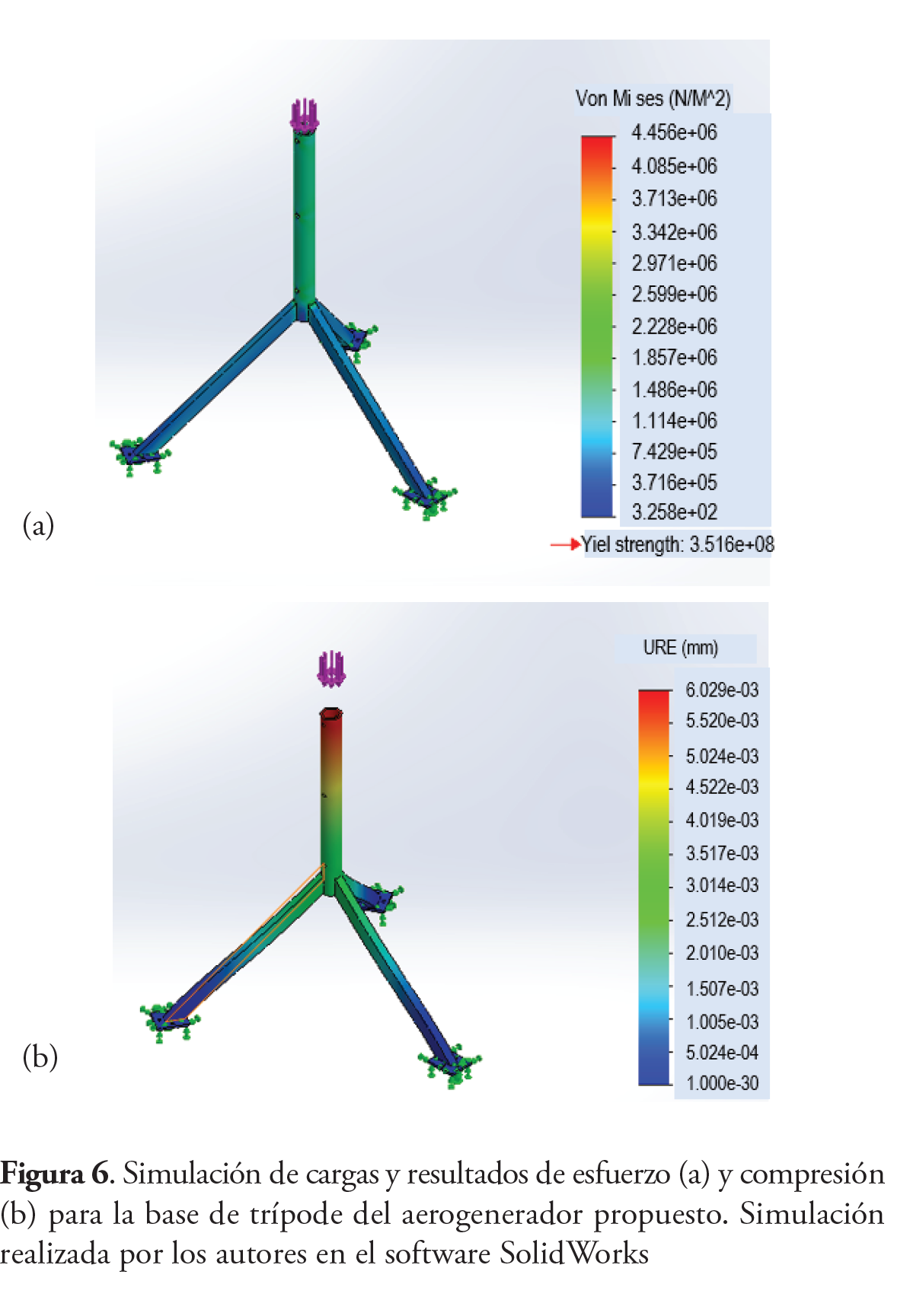
Se simuló la respuesta de la torre del aerogenerador propuesto aplicando una carga de 900 N, sobre la columna principal, el cual representa el peso total del sistema a sostener (Véase la figura 6).

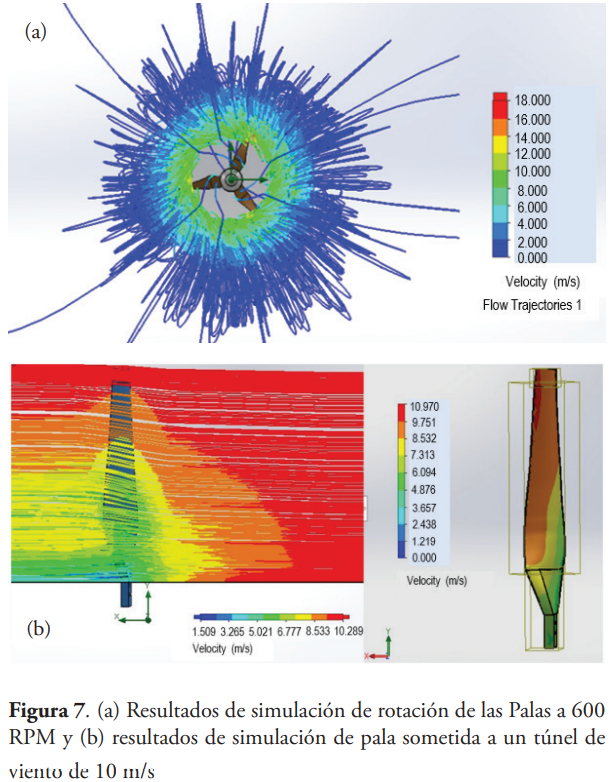
Simulación de rotación de las palas del rotor a 600 RPM

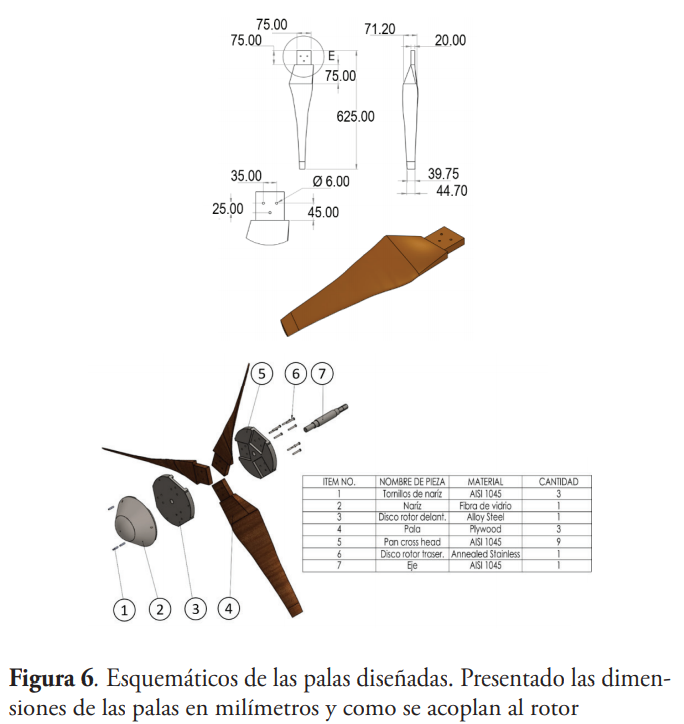
En el programa de simulación Flow Simulation no es posible determinar la velocidad de giro que produce una corriente de viento sobre las palas del aerogenerador. Sin embargo, puede hacerse el proceso inverso, es decir, girar las palas del aerogenerador para conocer el flujo de viento que produce. Es por esto que en el experimento a la inversa para comprobar que si las palas giran a 588 RPM, entonces el viento generado es de 10 m/s y es posible producir 250 W. Exitosamente, se cumplieron los resultados esperados. En la figura 6 se presenta el modelo propuesto de las palas y en figura 7 y figura 8 los resultados simulados de las palas en el software SolidWorks.

Análisis económico

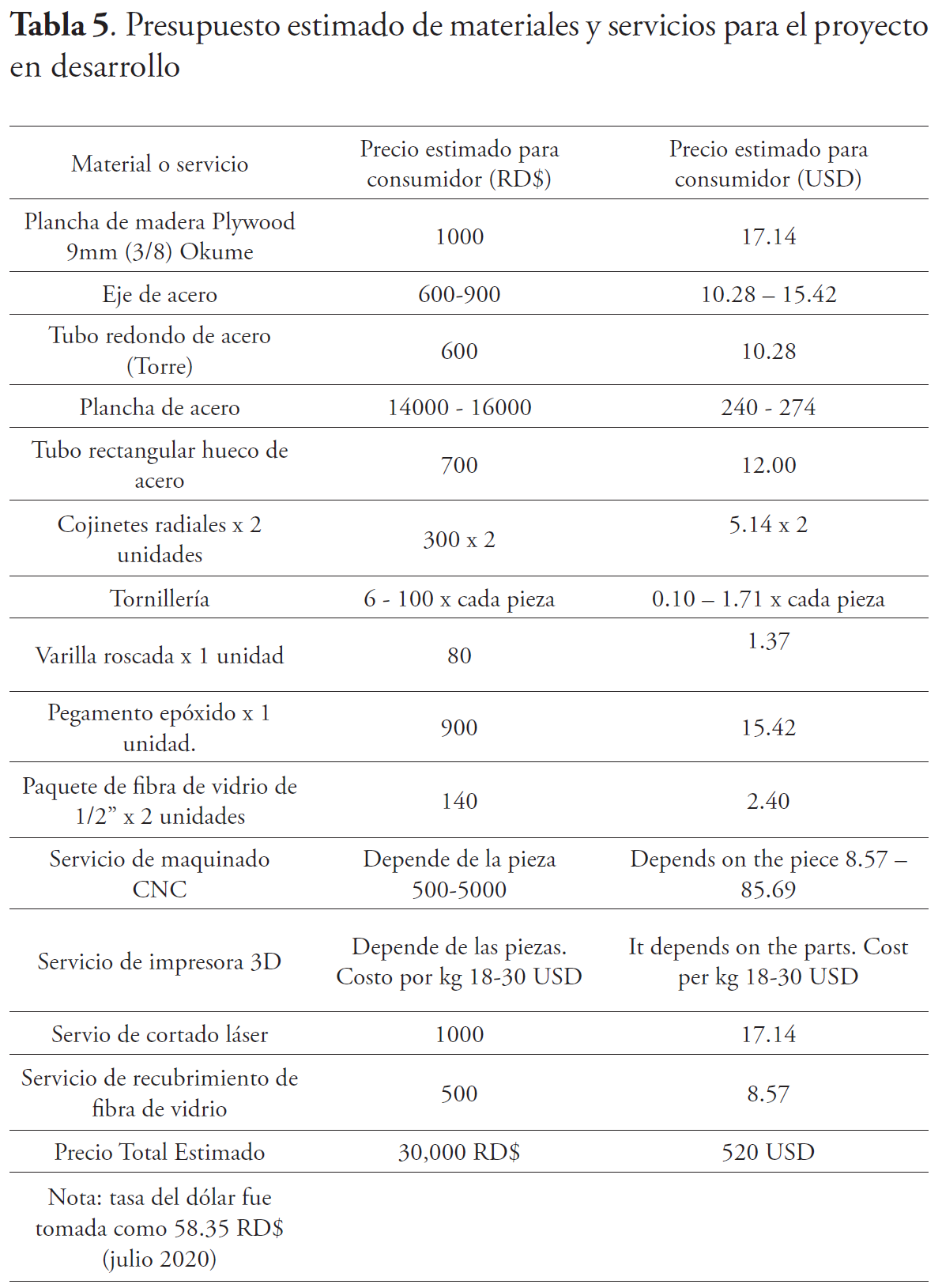
Los costos de este proyecto se estimaron con base en los precios ofertados en ferreterías y talleres industriales locales. Cabe destacar que estos precios no son definitivos, varían según la inflación monetaria, por lo que al momento de construir este proyecto es recomendable revisar esta tabla de precios como referencia, se sugiere mantener los gastos al mínimo.

Se debe resaltar que este prototipo está conceptualizado con la finalidad de que pudiera ser elaborado por cualquier persona que desee implementar estas técnicas para construir sus propias palas mecánicas.

En el mercado moderno se pueden encontrar distintos tipos de modelos de aerogenerador de baja potencia de 400W, 1000 W a un costo menor que el propuesto, estos oscilan entre 200 y 300 dólares. Sin embargo, la diferencia fundamental es la durabilidad y resiliencia de las partes presentadas en este diseño, con una vida útil de 20 años (Herrmann, Rauert, Dalhoff, & Sander, 2016) en las condiciones de trabajo con alta exposición solar, humedad, alta velocidad de los vientos y lluvias. Es por esto que se recomienda como una opción tanto para la República Dominicana como en toda la región del Caribe que presente las mismas condiciones. Como agregado se pueden aumentar el tamaño de las palas, para obtener mayor capacidad de producción de energía.

A continuación, presentaremos los precios analizando los materiales necesarios para su construcción como se expone en la tabla 5.

Impacto medioambiental 

La madera Plywood, aunque es elaborada en un proceso de compactación caliente no queda exenta de sufrir efectos de descomposición cuando se encuentra a la intemperie, por esta razón, para esta aplicación se utilizó un recubrimiento de fibra de vidrio para brindar una protección total de la madera por medio del encapsulamiento de las palas en este tipo de resina.

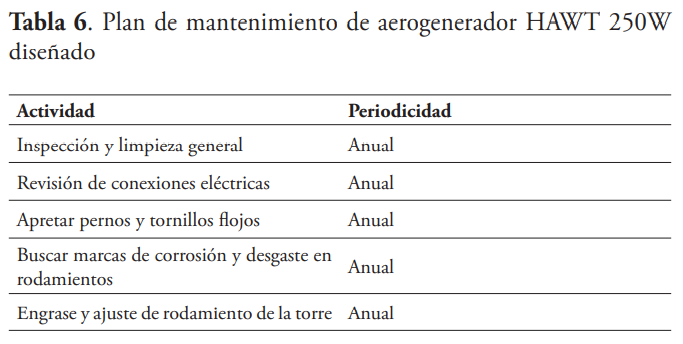
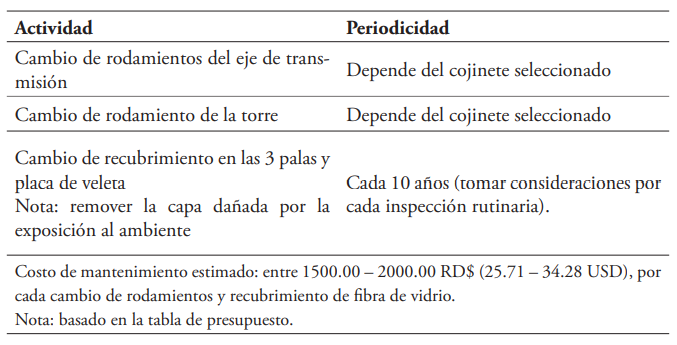
La fibra de vidrio convencional sin recubrimientos especiales tiene un tiempo de descomposición aproximado de 50 años bajo condiciones de cuidados especiales (Rahimizadeh, Kalman, Fayazbakhsh, & Lessard, 2019), cuando es expuesto a los rayos ultravioleta este tiempo de vida decrece aproximadamente a 4 años. La solución para el alargamiento de la vida útil de la resina es un aditamento de protección llamado Gelcoat, el cual es un material parecido a la resina, pero con bases de poliéster insaturado y resinas epóxicas (Rafiee et al., 2019). El Gelcoat ofrece durabilidad y resistencia al estrés mecánico brindándole un tiempo de vida aproximado de 15 años expuesto a la intemperie (Pomázi & Toldy, 2021). Al culminar el tiempo de vida estimado de dichos aerogeneradores se han estipulado varios proyectos encaminado a la reutilización de estos materiales, volviendo todavía más amigables al planeta estas maquinarias (Joustra, Flipsen, & Balkenende, 2021). En la tabla 6 se presenta el plan de mantenimiento básico del aerogenerador.

Este proyecto de diseño de palas mecánicas para aerogeneradores HAWT de 250 W se ha desarrollado dentro del INTEC, y puede considerarse como un proyecto piloto, como una primera parte de una serie de investigaciones orientadas a la parte mecánica de los aerogeneradores en lugares de bajos recursos. Este se presenta como un punto de partida, dando lugar para la mejora del diseño fortalecido en el análisis, prueba y experimentación con el prototipo que se fabrique.

Conclusiones

De acuerdo con la investigación realizada, el proyecto propuesto para el diseño mecánico de un aerogenerador de eje horizontal de 250 W constituye una opción viable y simple para las comunidades con escasez de energía eléctrica, por poseer una cantidad mínima de partes móviles. Teniendo siempre en cuenta que se debe realizar mediciones de viento para determinar la altura a la que se obtienen velocidad de viento de entre 10-11 m/s, que es donde se puede implementar este diseño que se apoya en los estudios de la NREL y las fórmulas del documento Introducción a teoría de las turbinas eólicas (Voneschen, 2009).

El prototipo reúne las características básicas y funcionales para su operación continua durante un tiempo de vida útil de 20 años, con un plan de mantenimiento preventivo de bajo coste, por tratarse de una máquina con pocas piezas móviles, tanto en las partes mecánicas como en el generador eléctrico diseñado en INTEC. El procedimiento de fabricación de moldes de madera de las palas por costillas es una de las propuestas con valor agregado al proyecto, el cual se convierte en una forma reutilizable y práctica para construir palas de aerogeneradores.