Ciencia, Ingenierías y Aplicaciones, Vol. 3, No. 2, julio-diciembre, 2020 ISSN (impreso): 2636-218X • ISSN (en línea): 2636-2171 • Sitio web: https://revistas.intec.edu.do/
Emergence of self-sustained oscillations in a hypothetical metabolic pathway regulated by a positive feedback loop
Aparición de oscilaciones autosostenidas en una ruta metabólica hipotética regulada por un bucle de retroalimentación positiva
Cómo citar: Boluda, C. J., Ceballos, M., Díaz, K., Hernández, D., Hidalgo, D., & Martínez, P. (2020). Aparición de oscilaciones autosostenidas en una ruta metabólica hipotética regulada por un bucle de retroalimentación positiva. Ciencia, Ingenierías y Aplicaciones, 3(2), 5-38. Doi: https://doi.org/10.22206/cyap.2020.v3i2.pp5-38
Introduction
1.1 Oscillations in chemical and biological systems
In the early 1950s, Russian biochemist Boris Pavlovich Belousov discovered that the oxidation of citric acid, with bromate (BrO3-) and cerium ions as a catalyst, did not progress as expected. Instead of a gradual change from a colorless solution to a pale yellow one, due to the oxidation of Ce3+ to Ce4+, periodic fluctuations in the color of the reaction mixture were observed, indicating that successive interconversions between reduced and oxidized states of reactants were taking place. Belousov was unsuccessful in publishing his results because the reviewers believed that this phenomenon disagreed with the Second Law of Thermodynamics (Kiprijanov, 2016). However, in 1961 Zhabotinsky verified Belousov’s discovery, publishing his results in 1964 (Tyson, 1994). The Belousov-Zhabotinsky reaction is considered a prototype of an oscillatory chemical reaction, being its mechanism well-known (Noyes et al., 1972). Nevertheless, oscillations in chemical systems were discovered long before. As early as the 17th century, Robert Boyle observed the intermittent ignition of phosphorus (Agreda & Barragán, 1998), and references from the 19th century mention the mercury beating heart, an electrochemical-based mechanical oscillator (Martín & Martín, 2010). In 1910 Lotka proposed a hypothetical reaction model that displays damped oscillations (Lotka, 1910).
Later on, in 1920, the same author showed that chemical systems could adopt sustained oscillatory behavior under certain circumstances (Lotka, 1920). However, it was not until the late 1960s when other researchers became interested in these types of reactions (Goldbeter, 2018). In 1956 Prigogine and Balescu demonstrated that sustained oscillations could occur in open chemical systems with nonlinear kinetics and far from equilibrium (Prigogine & Balescu, 1956; Goldbeter, 1996). In the 1960s, Goodwin studied negative feedback as a source of oscillations and the quasiperiodic and subharmonic behavior resulting from the interaction between two oscillators. Goodwin ventured the importance of these phenomena for cellular physiology (Gonze & Ruoff, 2020). In 1967 Prigogine and Nicolis demonstrated that sustained oscillations do not contradict any thermodynamic principle and showed that the instability of these chemical oscillators is due to positive (PFBLs) or negative feedback loops (NFBLs) (Prigogine & Nicolis, 1967; Agreda & Barragán, 1998).
In 1968 Lefever, Nicolis and Prigogine presented an autocatalytic theoretical model known as Brusselator (an acronym for Brussels and oscillator) that has been very useful for the understanding of oscillatory behaviors in chemical systems (Lefever et al., 1967; Goldbeter, 1996; Agreda & Barragán, 1998). In contrast to the scarcity of oscillatory behavior in chemical systems, rhythmicity is inherent to life (Li & Yang, 2018). Although periodic phenomena are not exclusive to biological systems, this behavior is much more frequent in living beings than in purely chemical systems (Goldbeter, 1996; Goldbeter, 2018). The circadian rhythm of sleep and wakefulness is a classic example of rhythmicity in which both frequency and amplitude of a circadian oscillator must keep robust 24-hour rhythms in the presence of external fluctuations (Kang & Cho, 2017). Although oscillations are necessary for many biological functions that require precise control of time, biological systems are inherently noisy, affecting its oscillations’ accuracy.
However, these systems achieve robustness by dissipating a critical amount of free energy, which results in greater irreversibility and accuracy of the oscillations (Cao et al., 2015; Fei et al., 2018). The relationship between the amount of energy dissipated and the precision of the oscillations period is a particularly topical question that has been the subject of recent research (del Junco and Vaikuntanathan, 2020). Heart and respiratory rates, fluctuations in hormone levels, electrically excitable cells like neurons, or muscle cells are additional examples of rhythmicity. Physiological oscillations can be a consequence of the central nervous system’s activity, although in certain instances, they are generated in situ. Thus, the heart rate is due to the sinoatrial node’s pacemaker cells, located in the right atrium, which have an unstable resting membrane potential.
Rhythmically and spontaneously, these cells generate an action potential that is transmitted with the necessary delay to coordinate the atria and ventricles’ function throughout the myocardium whose cells are electrically coupled. The frequency of the oscillations can become high; for example, in those insects equipped with asynchronous flying muscles, as Diptera, the wings can reach, in certain species, a frequency of 1000 Hz (Ruppert & Barnes, 1996). Oscillatory behavior is also observed in non-excitable cells, such as intracellular Ca2+ fluctuations, enzymatic reactions, or the secretion of many hormones released from the endocrine glands in a pulsatile manner rather than continuously (Goldbeter, 2018). Additional examples of oscillatory behaviors in non-excitable cells are the nuclear factor kappa B (NF-κB), and the proteins p53 and p38 (Li & Yang, 2018). The latter is a mitogen-activated protein kinase (MAPK), which controls an inflammatory response; oscillations in its activity have been observed for more than 8 hours under stimulation by interleukin-1β (Tomida et al., 2015).
The tumor suppressor protein p53, regulated through a negative feedback loop (NFBL) with the mdm2 protein, also exhibits an oscillatory dynamic. This mechanism allows the cell to repair its DNA through the action of p53 without excessive exposure to said protein, which could induce the apoptotic cell-death (Bar-Or et al., 2000). The oscillations of p53 are observed in cell lines of different species, although with different frequencies. For example, in rodent cells, these oscillations are faster than those observed in cell lines derived from humans, monkeys, and dogs (Stewart-Ornstein et al., 2018). Nuclear factor-kappa B (NF-κB), a protein complex that plays a crucial role in inflammation and cancer, exhibits damped oscillations synchronized with external disturbances (Zambrano et al., 2016).
1.2 Biochemical oscillations
The study of oscillating biochemical systems began in 1955 after observing changes in the concentrations of 3-phosphoglycerate and ribulose-1,5-diphosphate during the dark phase of photosynthesis (Chance et al., 1973). Oscillations in glycolysis were observed in 1957, while continuous glycolytic oscillations in cell-free yeast systems were demonstrated in 1966. (Chance et al., 1973; Agreda & Barragán, 1998; Robles & Barragán, 2006). Oscillations of cAMP (Li & Goldbeter, 1990; Goldbeter, 2018), intracellular Ca2+ (Dupont & Goldbeter, 1992), and glycolysis metabolites (Goldbeter, 1996) are among the best-known examples of periodic behavior at the biochemical level. The role of oscillations can be diverse and have high functional importance; abnormalities in them can cause disease, including cancer (Li & Yang, 2018). It has been suggested that they may be at the origin of some circadian rhythms and other processes such as cell division (Rodríguez et al., 1998). Thus, in Dyctiostelium discodeium amoebas, concentration’s periodic oscillations are related to the aggregation of cells that respond chemotactically to cAMP pulses (Goldbeter 1996; Goldbeter, 2018).
Periodic and chaotic behaviors are observed in metabolic pathways driven by matter flows and controlled by positive or negative feedback loops (PFBLs or NFBLs) (Goldbeter, 1996). In the context of biochemical pathways, feedback loops (FBLs) consist of at least two metabolites that regulate their activity reciprocally by activation or inhibition. The complex behavior of biological systems results from the coexistence of multiple of these FBLs (Dalchau et al., 2018).
Glycolysis is considered the central route of glucose catabolism and provides cells a significant portion of energy and pyruvate that can continue the subsequent oxidative degradation. It is a 10-steps metabolic pathway that transforms glucose and other hexoses into two pyruvate molecules, obtaining two molecules of ATP and NADH. This metabolic pathway begins and ends with irreversible steps: the conversion of glucose to glucose-6-phosphate by hexokinase, consuming ATP (step 1), and the conversion of phosphoenolpyruvate to pyruvate by pyruvate kinase, producing ATP (step 10). There is a third irreversible step: the transformation of fructose-6-phosphate to fructose-1,6-bisphosphate by phosphofructokinase (PFK). These three irreversible steps suppose a greater dissipation of energy, driving glycolysis away from thermodynamic equilibrium (Robles & Barragán, 2006).
Metabolic oscillations in this pathway have been observed in tumor cells, muscle extracts, fibroblasts, and yeast, the latter being the most studied system (Sel’kov, 1968; Robles & Barragán, 2006). These oscillations emerge in glycolysis when glucose-6-phosphate or fructose-6-phosphate is supplied, but not for the addition of fructose-1,6-diphosphate. This observation suggests that the enzyme phosphofructokinase (PFK) is the oscillophore responsible for the periodic behavior of the pathway, which can also be demonstrated by adding inhibitors or activators of the enzyme. Specifically, the addition of ADP (an activator of PFK) affected the frequency and amplitude of the oscillations of glycolytic metabolites; this is an example of PFBL.
Although PFBLs exerted by a product of a metabolic pathway on an enzyme are not as frequent as product inhibition, autocatalysis has an essential role in biochemical oscillations (Robles & Barragán, 2006; Tyson, 2002). Nonetheless, the importance of PFK in the oscillations observed in this metabolic pathway has also been relativized, proposing that the characteristics of the oscillations also depend on other enzymes of the pathway (Reijenga et al., 2005). Alternatives to the oscillophore have been proposed to explain this glycolytic behavior through the autocatalytic character of the stoichiometry of the pathway, which acts as a PFBL responsible for the oscillations (Gustavsson et al., 2014).
The theoretical approach to these periodic biochemical phenomena through models is useful in understanding their physiological roles and underlying mechanisms. An example of the latter is the Oregonator, an autocatalytic model that reproduces the oscillatory behavior of the Belousov-Zabotinsky reaction (Field & Noyes, 1974).
This article presents a hypothetical metabolic pathway with a PFBL. The system is kept away from thermodynamic equilibrium by constant input and output fluxes. The positive feedback consists of the activation of the first enzyme of the pathway by its product. Our main target is to provide a simple kinetic model in which, intrinsically and under certain conditions, sustained oscillatory behavior arises. Such a model could be a starting point for building modified or more complex and realistic models for educational and research purposes.
2 Model and kinetic equations
Figure 1 shows the sequence of enzymatic reactions of a hypothetical linear metabolic pathway consisting of four steps and six metabolites: S0, S1, S2, S3, S4, and S5. The concentration of S0 is constant and it is also converted at a constant rate by a non-enzymatic irreversible step in S1, representing a non-rhythmic input of the substrate into the system. The rest of the metabolites are sequentially transformed from S1 to S5 through the subsequent action of the enzymes E1, E2, E3, and E4.
Figure 1. Sequential reactions that make up a linear metabolic pathway
As described in Figure 2, each enzyme reversible binds to its substrate in these four enzymatic reactions, forming a substrate-enzyme complex (Ex Sx ) that converts into the corresponding product. The kinetic constants for the reversible formation of the substrate enzyme complex are given by kn and k-n. For each step of the pathway, the substrate enzyme complex (Ex Sx ) yields its corresponding product (Sx+1) with a kinetic constant denoted by kn + 1 and k(n+1)-1 for the reverse reaction. When k(n+1)-1= 0, the conversion of Ex Sx into Ex and Sx+1 is irreversible.
Figure 2. Enzyme reversibly binds its substrate forming a substrate-enzyme complex
Note: Each enzyme of the pathway reversibly binds its substrate to form an enzyme-substrate complex (ExSx) with kn and k-n as kinetic constants of the direct and reverse reaction. The ExSx complexes evolve to form their corresponding products (Sx+1) with a constant rate of kn+1.
The dynamic of the enzymatic conversions showed in Figure 1 can be described by the following differential equations:
As shown in Figure 1, the E1-catalyzed transformation of S1 to S2 simulates an activation per product step. The formation reaction rate for the E1S1 complex and its conversion into E1 and S2 have become strongly dependent on the concentration of S2 by the inclusion of the algebraic expression 1+ [S2]3 in equations 1 and 2. This represents an activation of the E1 enzyme by the substrate S2, increasing both the affinity of the enzyme E1 to the substrate S1 and the conversion rate of this complex to S2 and E1. The inclusion of the binomial 1+ [S2]3 in the differential equations is responsible for the system’s non-linearity. According to the Arrhenius equation, the kinetic constants depend not only on the temperature but also on the presence of catalyst; therefore, it can be considered that the expression (1+S23) modifies the kinetic constants as follows: k1’ = k1 (1+S23) and k2’ = k2 (1+S23).
Since in living cells, the inlet flow is considered a key parameter to trigger the oscillations (Danø et al., 1999); the model›s behavior was evaluated for concentration values of S0 between 0 and 12 arbitrary units (a.u.). In all experiments, the inlet flux was such that the concentration of S2 (activator of E1) was lower than the concentration of E1 ([S2] < [E1]). Table 1 shows the values of the kinetic parameters, concentration of enzymes, and initial substrates concentration for each of the pathway steps.
Python version 3.7.4 with Spyder and Anaconda as IDE was used for numerical integration of differential equations. The simulations were performed, implementing the kinetic parameters and concentration values for metabolites and enzymes shown in Table 1. Python script used for the experiments is provided in the supplementary materials.
Results
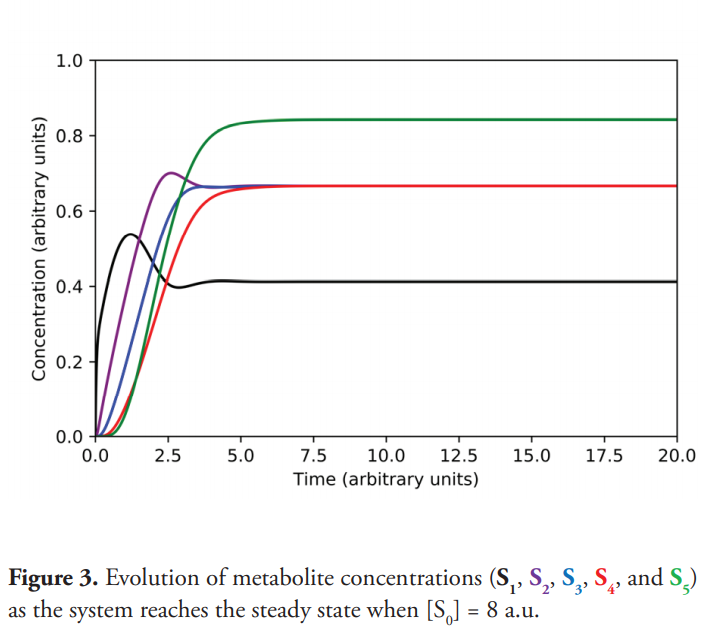
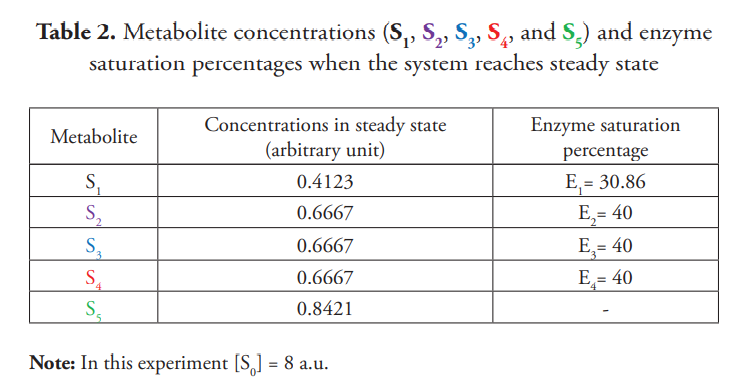
Using the values specified in Table 1 and for [So] equal to 8 a.u., the system reaches the steady state (Figure 3) with saturation percentages for enzymes not exceeding 40%. The steady state concentrations of metabolites and enzyme saturation percentages are shown in Table 2.
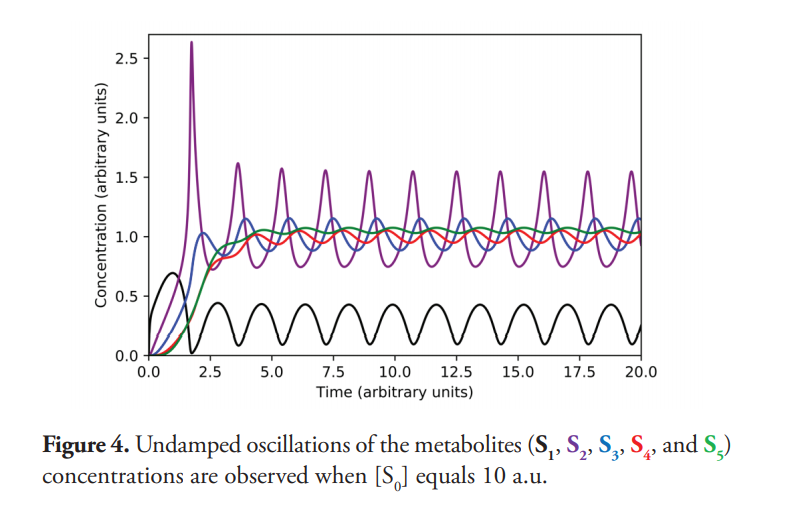
However, when [S0] = 10 a.u., the system does not reach a steady state but is installed in a sustained oscillation, as displayed in Figure 4. Periodic oscillations with T=1.775 a.u. are observed in all metabolites of the pathway. The transformation of S1 to S2 speeds up as S2 increases until S1 depletion (Figure 1), limiting S2 production to a value that allows recovery of S1 levels, this being a classic oscillation generator mechanism (Tyson, 2002).
The oscillatory ranges of the concentration of metabolites are shown in Table 3.
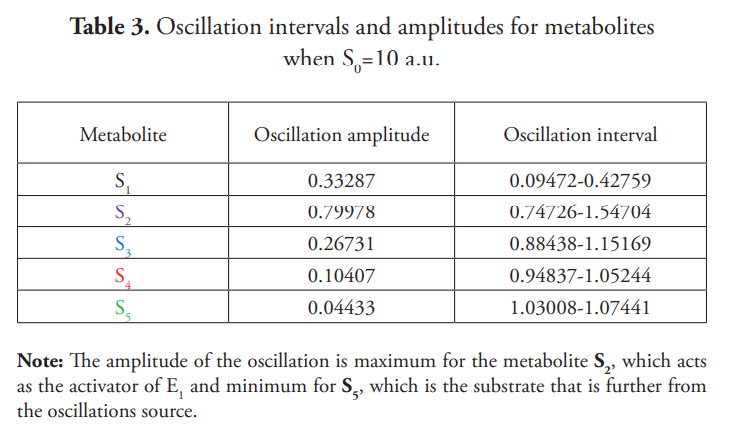
Figure 5 illustrates the phase plane plot for S2 against S3, observing a limit cycle that is the proper attractor for the oscillatory behavior.
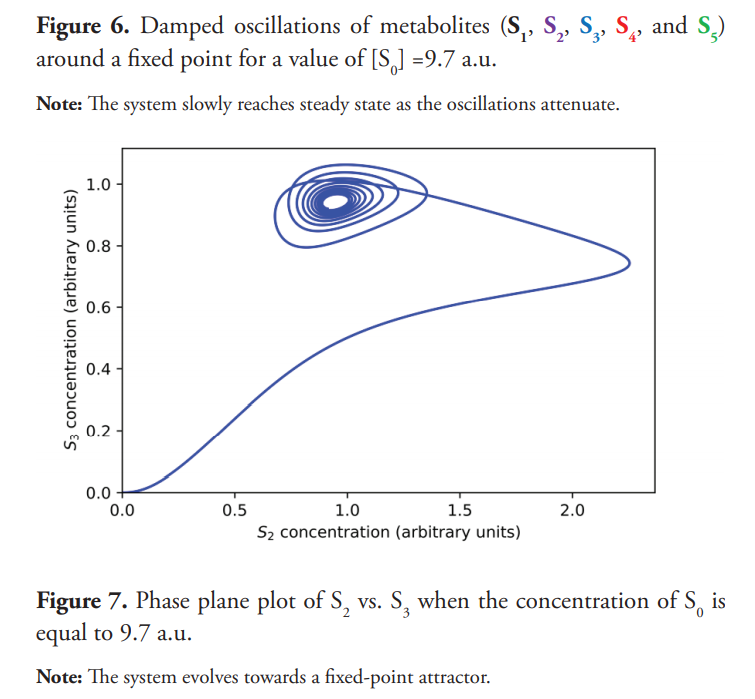
The transition from the steady state to the sustained oscillation takes place through a Hopf bifurcation (Gustavsson et al., 2014; Beta & Kruse, 2017). For a critical value of S0 (approximately 9.8 a.u.), the steady state becomes unstable, and the system evolves to an oscillatory behavior. When S0=9.7 a.u., near the bifurcation point, the system shows damped oscillations, which eventually reaches the steady state as shown in Figure 6. Figure 7 shows the phase plane for this experiment; a stable focus is attained. Figure 8 displays a close-up view of the said attractor.
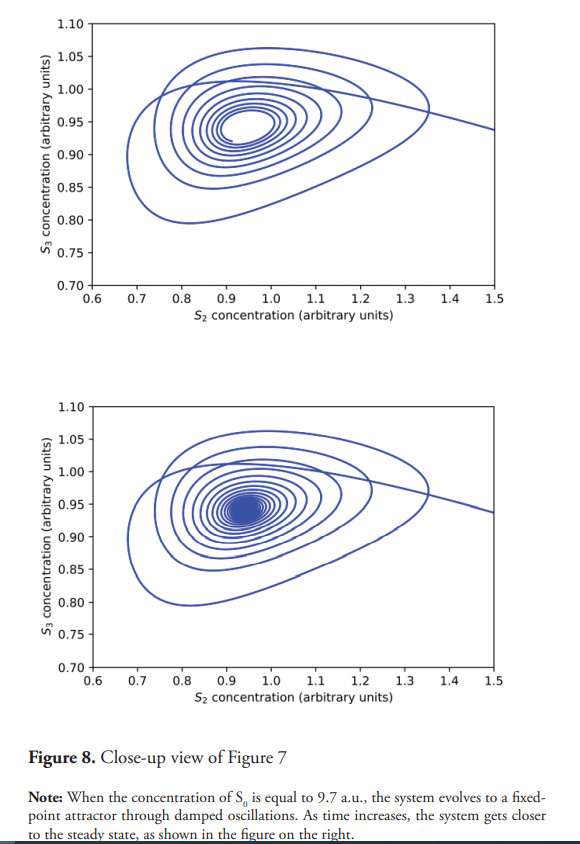
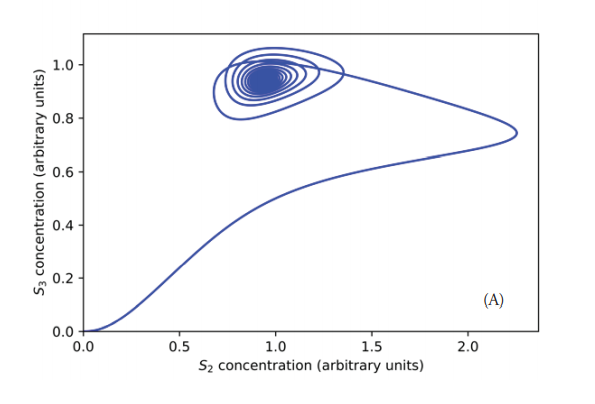
The system’s evolution from a fixed-point attractor towards the limit cycle has also been studied (Figure 9). As previously explained, when the concentration of S0 is equal to 9.7 a.u. the limit cycle is not achieved, resulting in a stable focus (Figure 9A). However, starting from a concentration of S0 equal to 9.8 a.u., a stable limit cycle starts taking shape as a result of the self-sustained oscillations, as described by Saha & Gangopadhyay (Saha & Gangopadhyay, 2017). This tendency is confirmed for concentration values of S0 equal to 9.9 and 10 a.u., for which their corresponding phase planes are presented in Figure 9, labeled as (C) and (D). The system returns to a steady state when the concentration of S0 is equal or higher than 11.75 (a.u.), as demonstrated in Figure 10. It should be clarified that the emergence of oscillatory behavior also depends on the concentrations of the enzymes. For example, changing the concentrations of E1, E2, E3, and E4 to 15 a.u. and [S0] equal to 10 a.u., the system does not oscillate. Instead, it reaches a steady state, thus making the oscillatory window even narrower. Contrary to what happens within the oscillatory interval, the concentration of S2 did not drop enough to allow a significant increase in S1, which remains at low concentration, being this the probable reason for the lack of oscillations.
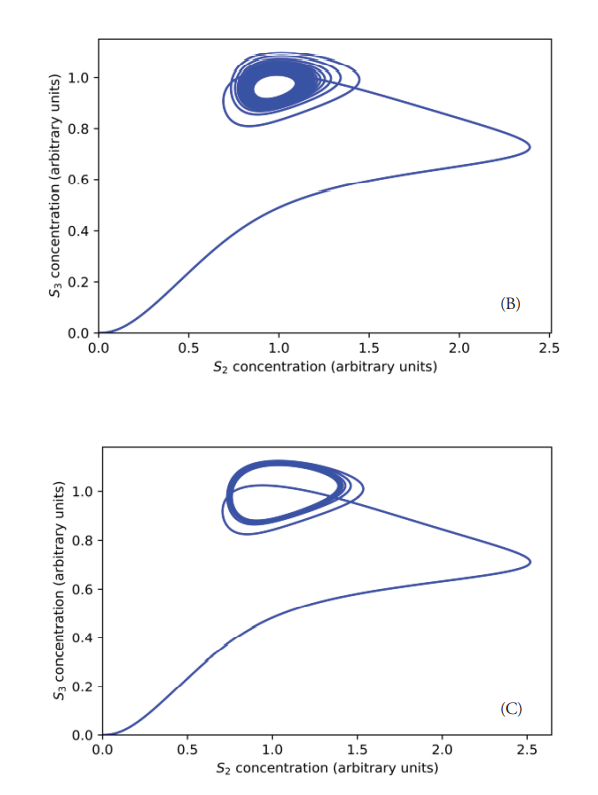
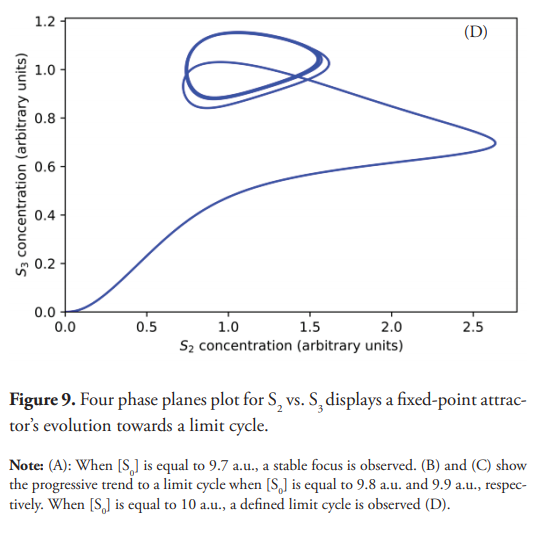
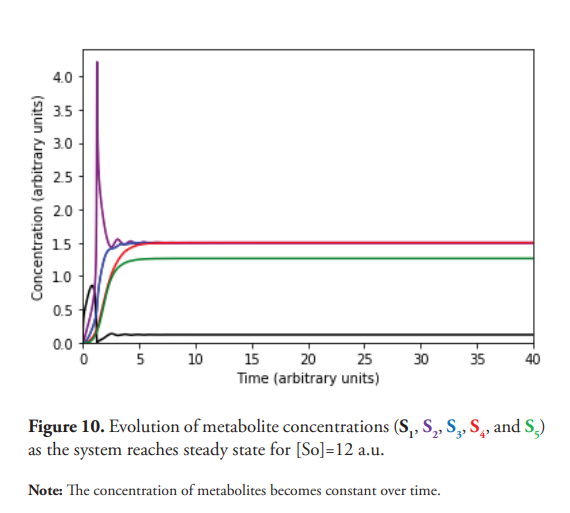
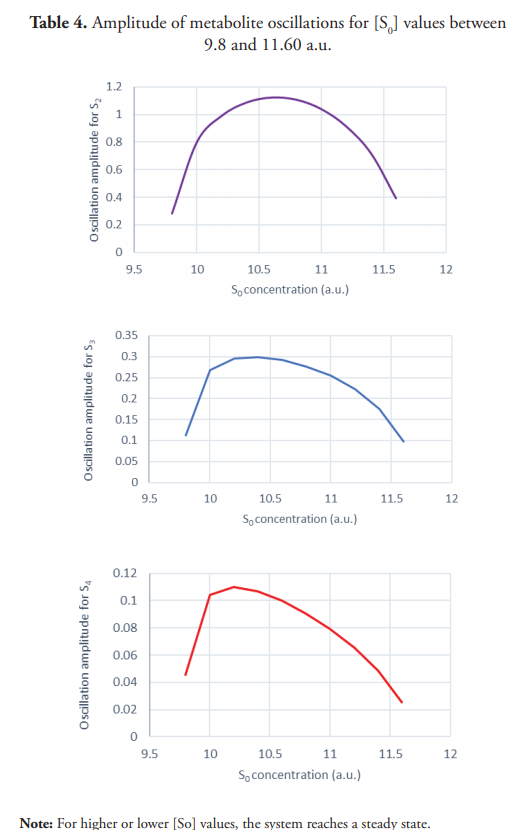
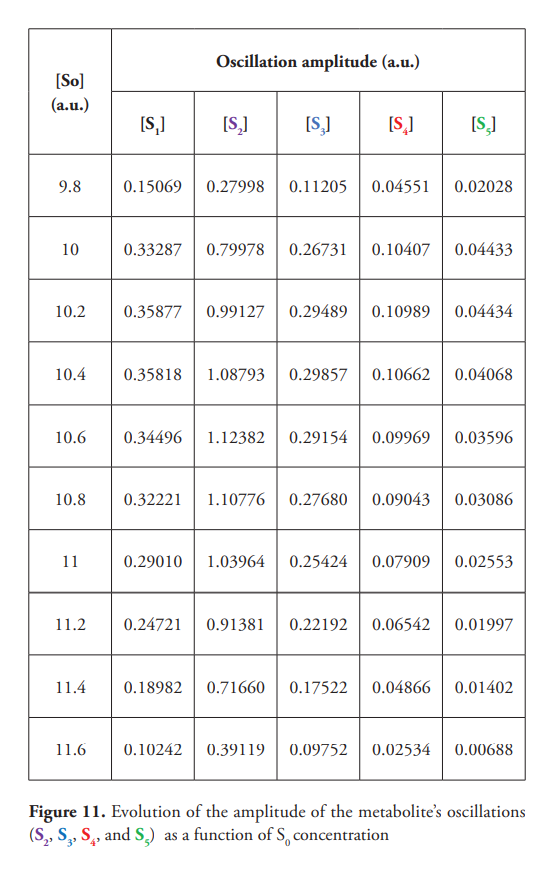
Table 4 shows the amplitude of metabolites’ oscillation as a function of [S0]. Different metabolites reach maximum oscillations for different values of S0. As displayed in Figure 11, oscillations’ amplitude decreases progressively until the system returns to a steady state. Sustained oscillatory behavior is observed in a narrow interval of S0 values (approximately 9.8-11.6 a.u.). Outside this interval, the system remains in steady state, which is reached through damped oscillations near the oscillatory behavior’s emergence point.
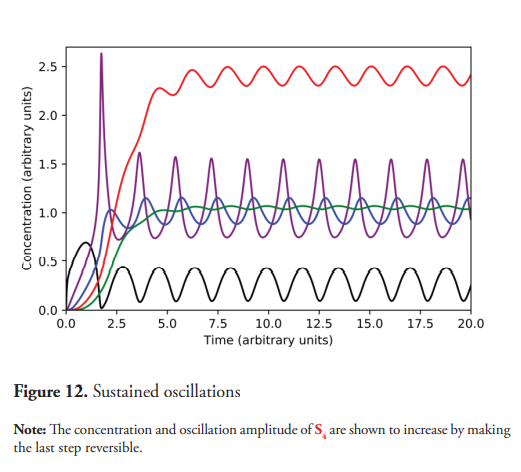
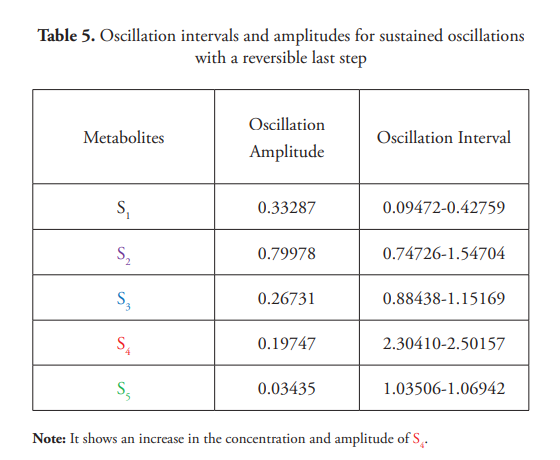
The effect of the reversibility of the pathway’s steps was also briefly analyzed. Setting the value of K-8 to 2, instead of the previously stated value of k-8 =0, the conversion of E4S4 into S5 becomes reversible (Figure 2). This means E4 can bind S5 to regenerate the E4S4 complex that could in turn dissociate, leading to a higher concentration of S4. As can be seen in Figure 12, when the last step of the pathway is reversible, the oscillations amplitude of S4 have a wider interval than those shown in Figure 4, which corresponds to a simulation where the last step is irreversible. The concentration intervals and its oscillation amplitudes of these metabolites are shown in Table 5.
This experiment demonstrates that the oscillation’s characteristics will depend not only on the oscillophore, but also on the kinetic parameters of other metabolic pathway steps.
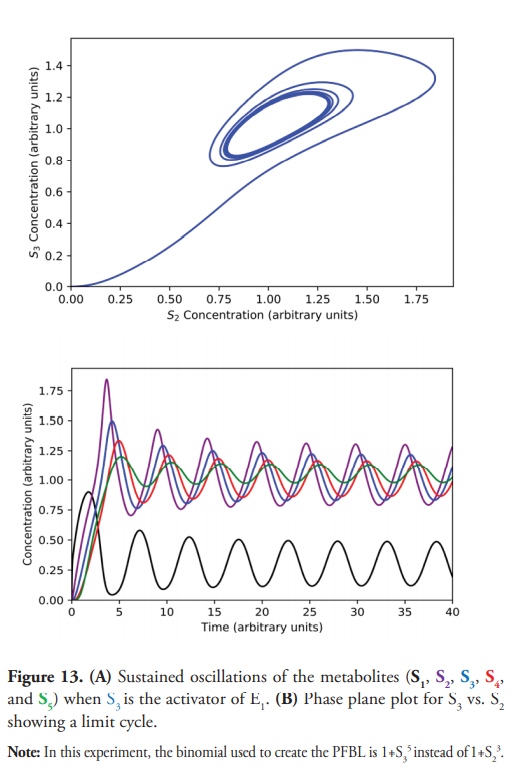
The model could be easily modified to simulate different metabolic pathways such as branched, cyclic routes, or to implement additional feedback loops (PFBLs or NFBLs) for educational or research purposes. For instance, Figure 13A shows the undamped oscillations observed when S3, instead of S2, is the activator of E1 for a [S0] equal to 10 a.u. Figure 13B shows the expected limit cycle for S3 vs. S2.
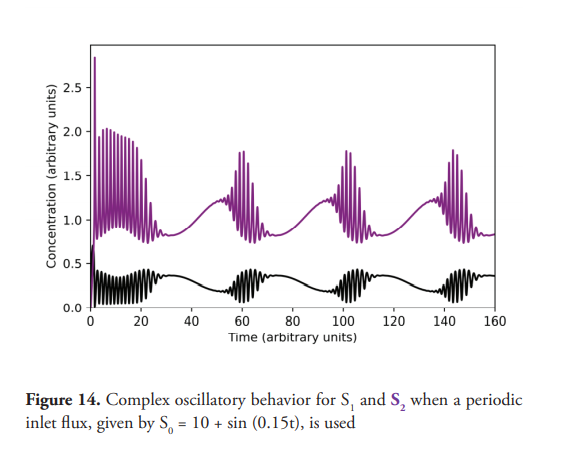
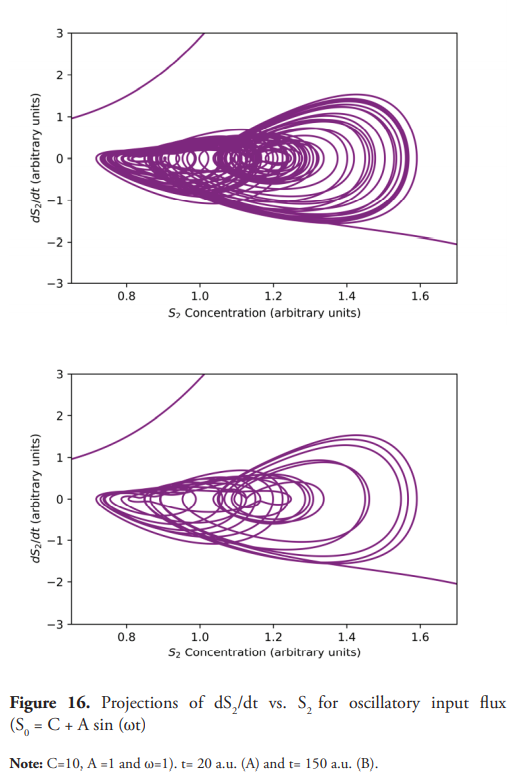
The effect of changing the constant input flux for a sinusoidal type input flux was also investigated. As previously shown, for constant inlet fluxes, steady states or sustained oscillations are observed. In contrast to this, an oscillatory input given by S0 = C + A sin (ωt) leads to more complex behavior as demonstrated in Figure 14; the value 11.0 a.u. for [S0] triggers the sustained oscillations, returning to a non-oscillatory state when So=9.0 a.u. which being a periodically excitable system.
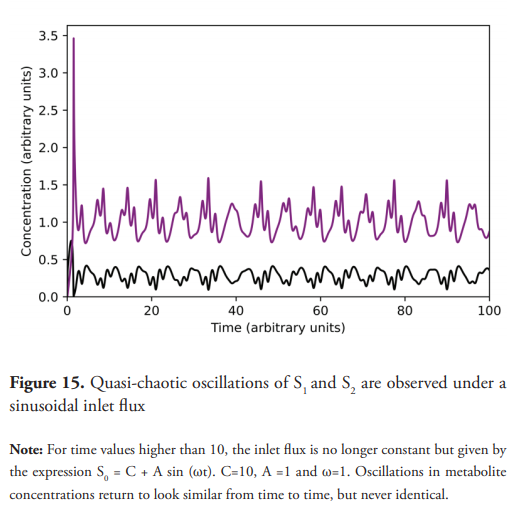
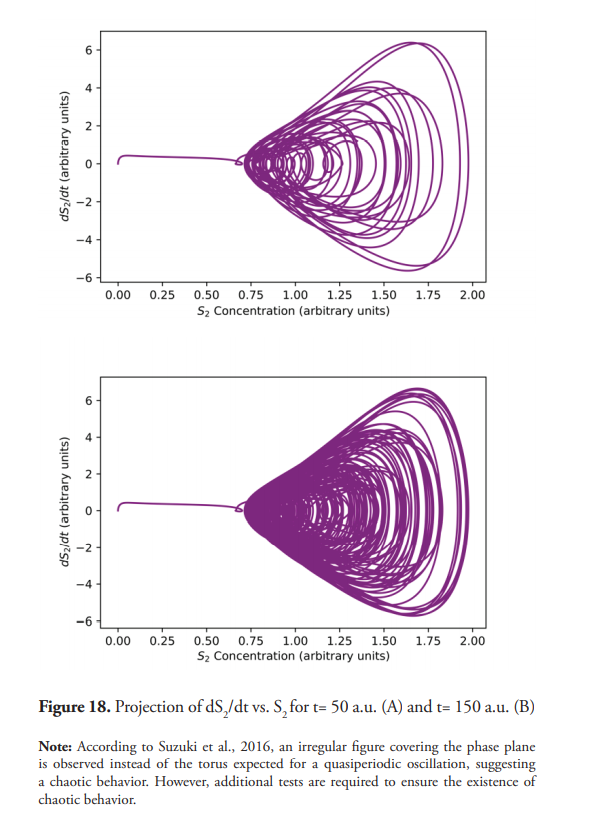
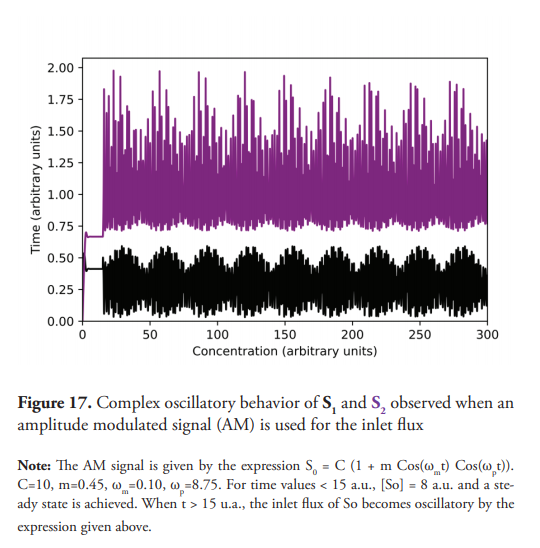
Quasi-chaotic oscillations are observed (Figure 15) when C=10, A =1, and ω=1. Figure 16 shows the projections of dS2/dt vs. S2. Figure 17 shows even more complex and irregular oscillations when an amplitude modulated signal (AM) is used for the inlet flux. Figure 18 shows the phase plane of dS2/dt vs. S2, which seems to indicate a chaotic dynamic (Suzuki et al., 2016). However, quasiperiodic behavior, or even long period oscillations can result in an ergodically filled torus with a similar appearance to a chaotic attractor (Derrick, 1993). Therefore, although the emergence of chaos as a consequence of a forced oscillatory input in a nonlinear system is well known (Nikolaev et al., 2018), other tests are necessary to ensure its existence, such as the determination of Lyapunov exponents, in addition to the detailed study of the trajectories in the phase plane. These last two experiments show interesting results (Figures 15 and 17) for developing further studies about the nature of the observed dynamics, derived from the change oduponf the model’s original conditions.
4. Conclusions
The behavior of the model was evaluated for S0 concentrations in the range 0-12 a.u., observing undamped oscillations for a narrow range of inlet flow values: [11.60>[S0]>9.8]. Outside this oscillatory interval, the system evolves towards a steady state. The transition between steady states and permanent oscillations take place through damped oscillations. Whilst in the absence of the positive feedback loop the system does not exhibit oscillatory behavior, this is not the only requirement to generate the oscillations since they were shown to depend on enzyme concentrations, in addition to the inlet flow value.
Under a dynamic of sustained oscillations, it was found that the amplitude of the oscillations decreases with the distance to the oscillations source and depends on the value of the kinetic constants and the inlet flux. On the contrary, the phase shift of the oscillations increases with the distance to the oscillophore. Undamped oscillations are also observed when the activator is located further ahead in the sequence of the transformation, and not only when it is the direct product of the core of the oscillatory mechanism. When the system’s substrate input is changed from constant to oscillatory, more irregular oscillations emerge that could correspond to chaotic and quasi-chaotic behaviors.
Acknowledgments
Biotechnology bachelor students Ceballos M., Díaz K., Hernández D., Hidalgo D., and Martínez P. thank Carolina Juncá for the help in the understanding of Phyton Programming language. The order of authorship obeys only the alphabetical order of the surnames, as each author contributed to the same extent on the realization of this publication.
Referencias
Agreda, J. A. & Barragán, D. A. (1998). Reacciones químicas oscilantes: su historia, Revista Colombiana de Química, 27(2):61-70.
Bar-Or, R. L., Maya, R., Segel, L. A., Alon, U., Levine, A. J., & Oren, M. (2000). Generation of oscillations by the p53-Mdm2 feedback loop: A theoretical and experimental study. Proceedings of the National Academy of Sciences, 97(21):11250-11255. doi: https://doi.org/10.1073/pnas.210171597
Beta, C. & Kruse, K. (2017). Intracellular Oscillations and Waves. Annual Review of Condensed Matter Physics, 8:239-264. doi: https://doi.org/10.1146/annurev-conmatphys-031016-025210
Cao, Y., Wang, H., Ouyang, Q., & Tu, Y. (2015). The free energy cost of accurate biochemical oscillations. Nature Physics, 11(9):772-778. doi: https://doi.org/10.1038/nphys3412
Chance, B., Pye, E. K., Ghosh, A. K., & Hess, B. (Eds.). (1973). Biological and Biochemical Oscillators (1st ed.). New York: Academic Press.
Dalchau, N., Szép, G., Hernansaiz-Ballesteros, R., Barnes, C. P., Cardelli, L., Phillips, A., & Csikász-Nagy, A. (2018). Computing with biological switches and clocks. Natural Computing, 17(4):761-779. doi: https://doi.org/10.1007/s11047-018-9686-x
Danø, S., Sørensen, P. G., & Hynne, F. (1999). Sustained oscillations on living cells. Nature, 402(6759):320-322. doi: https://doi.org/10.1038/46329
del Junco, C. & Vaikuntanathanm, S. (2020). Robust oscillations in multi-cyclic Markov state models of biochemical clocks. Journal of Chemical Physics, 152(5):055101. doi: https://doi.org/10.1063/1.5143259
Derrick, W. (1993). Mathematics of chaos in perturbed oscillators. In Chaos in Chemistry and Biochemistry (pp. 1-20), World Scientific. doi: https://doi.org/10.1142/9789814354745_0001
Dupont, G. & Goldbeter, A. (1992). Oscillations and waves of cytosolic calcium: Insights from theoretical models. BioEssays, 14(7):485-493. doi: https://doi.org/10.1002/bies.950140711
Fei, C., Cao, Y., Ouyang, Q., & Tu, Y. (2018). Design principles for enhancing phase sensitivity and suppressing phase fluctuations simultaneously in biochemical oscillatory systems. Nature communications, 9(1):1-10. doi: https://doi.org/10.1038/s41467-018-03826-4
Field, R. J. & Noyes, R. M. (1974). Oscillations in chemical system. IV. Limit Cycle behavior in a model of a real chemical reaction. The Journal of Chemical Physics, 60(5):1877-1884. doi: https://doi.org/10.1063/1.1681288
Goldbeter, A. (1996). Biochemical Oscillations and Cellular Rhythms. The molecular bases of periodic and chaotic behaviour. Cambridge: Cambridge University Press. doi: https://doi.org/10.1017/CBO9780511608193
Goldbeter, A. (2018). Dissipative structures in biological systems: bistability, oscillations, spatial patterns and waves. Philosophical Transactions Royal Society A: Mathematical, Physical and Engineering Sciences, 376(2124):20170376. doi: https://doi.org/10.1098/rsta.2017.0376
Gonze, D. & Ruoff, P. (2020), The Goodwin Oscillator and its Legacy. Acta Biotheoretica. doi: https://doi.org/0.1007/s10441-020-09379-8
Gustavsson, A. K., van Niekerk, D. D., Adiels, C. B., Kooi, B., Goksör, M., & Snoep, J. L. (2014). Allosteric regulation of phosphofructokinase controls the emergence of glycolytic oscillations in isolated yeast cells. The FEBS journal, 281(12):2784-2793. doi: https://doi.org/10.1111/febs.12820
Kang, J. H. & Cho, K. H. (2017). A novel interaction perturbation analysis reveals a comprehensive regulatory principle underlying various biochemical oscillators. BMC systems biology, 11(1):1-12. doi: https://doi.org/10.1186/s12918-017-0472-7
Kiprijanov, K. S. (2016). Chaos and beauty in a beaker: The early history of the Belousov-Zhabotinsky reaction. Annalen der Physik, 528:(3-4): 233-237. doi: https://doi.org/10.1002/andp.201600025
Lefever, R., Nicolis, G., & Prigogine, I. (1967). On the occurrence of oscillations around the steady state in systems of chemical reactions far from equilibrium. The Journal of Chemical Physics, 47(3):1045-1047. doi: https://doi.org/10.1063/1.1711987
Li, Y. X. & Goldbeter, A. (1990). Frequency encoding of pulsatile signals of cAMP based on receptor desensitization in Dictyostelium cells. Journal of theoretical biology, 146(3):355-367. doi: https://doi.org/10.1016/s0022-5193(05)80746-5
Li, Z. & Yang, Q. (2018). Systems and synthetic biology approaches in understanding biological oscillations. Quantitative Biology, 6(1):1-14. doi: https://doi.org/10.1007/s40484-017-0120-7
Lotka, A. J. (1910). Contribution to the Theory of Periodic Reactions. The Journal of Physical Chemistry, 14(3):271-274. doi: https://doi.org/10.1021/j150111a004
Lotka, A. J. (1920). Undamped oscillations derived from the law of mass action. Journal of American Chemical Society, 42(8):1595-1599. doi: https://doi.org/10.1021/ja01453a010
Martín, M. T. & Martín, M. (2010). Corazón oscilante de mercurio. Anales de Química, 106(4):304-310.
Nikolaev, E. V., Rahi, S. J., & Sontag, E. D. (2018). Subharmonics and chaos in simple periodically forced biomolecular models. Biophysical journal, 114(5):1232-1240.
Noyes, R. M., Field, R., & Koros, E. (1972). Oscillations in chemical systems. I. Detailed mechanism in a system showing temporal oscillations. Journal of the American Chemical Society, 94(4):1394-1395. doi: https://doi.org/10.1021/ja00759a080
Prigogine, I. & Balescu, R. (1956). Phénomènes cycliques dans la thermodynamique des phénomènes irréversibles. Bulletin de la Classe des sciences. Académie royale de Belgique, 42:256-265.
Prigogine, I. & Nicolis, G. (1967). On Symmetry‐Breaking Instabilities in Dissipative Systems. The Journal of Chemical Physics, 46(9):3542-3550. doi: https://doi.org/10.1063/1.1841255
Reijenga, K. A., van Megen, Y., Kooi, B. W., Bakker, B. M., Snoep, J. L., van Verseveld, H. W., & Westerhoff, H. V. (2005). Yeast glycolytic oscillations that are not controlled by a single oscillophore: A new definition of oscillophore strength. Journal of Theoretical biology, 232(3):385-398. doi: https://doi.org/10.1016/j.jtbi.2004.08.019
Robles, E. & Barragán, D. (2006). Termodinámica de los procesos irreversibles de un metabolismo. Revista Académica Colombiana de Ciencias Exactas, Físicas y Naturales, 116:419-434.
Rodríguez, Y., Nuño, J. C., Lloréns, M., Sánchez-Valdenebro, J. I., & Montero, F. (1998). Amortiguamiento y desfase de las señales periódicas en rutas metabólicas. Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales, 92(2-3):269-277.
Ruppert, E. E. & Barnes, R. D. (1996). Zoología de los invertebrados (6th ed.). México: McGraw-Hill Interamericana.
Saha, S. & Gangopadhyay, G. (2017). Isochronicity and limit cycle oscillation in chemical systems. Journal of Mathematical Chemistry, 55(3):887-910. doi: https://doi.org/10.1007/s10910-016-0729-1
Sel’kov, E. E. (1968). Self-oscillations in glycolysis 1. A simple kinetic model. European Journal of Biochemistry, 4(1):79-86.
Stewart-Ornstein, J., Cheng, H. W., & Lahav, G. (2018). Conservation and divergence of p53 oscillation dynamics across species. Cell System, 5(4):410-417. doi: https://doi.org/10.1016/j.cels.2017.09.012.
Suzuki, Y., Lu, M., Ben-Jacob, E., & Onuchic, J. N. (2016). Periodic, Quasiperiodic and Chaotic Dynamics in Simple Gene Elements with Time Delays. Scientific Reports, 6(1):21037. doi: https://doi.org/10.1038/srep21037
Tomida, T., Takekawa, M., & Saito, H. (2015). Oscillation of p38 activity controls efficient pro-inflammatory gene expression. Nature Communications, 6(1):8350. doi: https://doi.org/10.1038/ncomms9350
Tyson, J. J. (1994). What everyone should know about the Belousov-Zhabotinsky reaction, In S. A. Levin (Ed.). Frontiers in mathematical biology (pp. 569-587). Berlin, Heidelberg: Springer.
Tyson, J. J. (2002). Biochemical oscillations (Chapter 9), In C. P. Fall, E. S. Marland, J. M. Wagner, & J. J. Tyson (Eds.). Computational cell biology (pp. 230-260). New York: Springer.
Zambrano, S., De Toma, I., Piffer, A., Bianchi, M. E., & Agresti, A. (2016). NF-κB oscillations translate into functionally related patterns of gene expression, eLife, 5:e09100. doi: https://doi.org/10.7554/eLife.09100.001

