Análisis probabilístico de peligro sísmico y terremoto de diseño para Santiago-República Dominicana

1. Introducción

La caracterización de los movimientos fuertes del suelo inducidos por terremotos en un sitio es un problema fundamental en ingeniería sísmica. Las características esperadas del movimiento del suelo, tales como intensidad, duración y contenido de frecuencia son necesarias para un efectivo análisis de los efectos inducidos en estructuras civiles y su diseño para resistir dichos efectos. La práctica actual, en el diseño de estructuras sismo-resistentes, está basada en permitir que la estructura sufra un nivel prescrito de daños durante terremotos fuertes, sin fallas importantes en el sistema estructural que pongan en riesgo su integridad; el nivel esperado de daños en la estructura puede ser severo e incluso irreparable. La razón de esta filosofía de diseño es que para estructuras convencionales no es económicamente factible diseñarlas para resistir los efectos de terremotos fuertes sin sufrir ningún tipo de daños, debido a que la recurrencia media de este tipo de evento extremo implica que hay una baja probabilidad de que una estructura particular sea afectada por un terremoto severo durante su vida útil.

La predicción de las características del movimiento del suelo inducido por terremotos en un sitio se conoce como un Análisis de Peligro Sísmico (APS). En general, este procedimiento conlleva los siguientes pasos (Villaverde, 2009)

• Identificación y caracterización de las fuentes de terremotos (fallas sísmicas) cerca del sitio.
• Estimación de la frecuencia de terremotos de distintas magnitudes que se pueden generar en las fallas (basado en datos históricos, medidos con instrumentos o resultados de estudios paleosísmicos).
• Evaluación de la distancia y orientación del sitio con respecto a las fuentes.
• Desarrollo y aplicación de relaciones empíricas (leyes de atenuación) para relacionar características de las fuentes con características del movimiento del suelo en el sitio.

El análisis de peligro sísmico se puede dividir en dos etapas principales: caracterización de las fuentes y caracterización del movimiento del suelo. Se debe resaltar que la predicción de las características de futuros terremotos y su efecto en un sitio es una tarea desafiante debido a las incertidumbres relacionadas al modelamiento de los mecanismos de iniciación y propagación de terremotos, y la escasez de datos o mediciones de sismicidad (especialmente para terremotos fuertes) necesarios para calibrar modelos basados tanto en conceptos físicos como estadísticos. Para tomar en consideración las incertidumbres relacionadas a la predicción de las características del movimiento del suelo en un sitio, generalmente, es utilizado un procedimiento probabilístico donde las variables con mayor incertidumbre se tratan como variables aleatorias (Cornell, 1968). Cuando un procedimiento probabilístico es utilizado para estimar parámetros sísmicos en un sitio, se conoce como un Análisis Probabilístico de Peligro Sísmico (APPS).

El APPS es la principal herramienta utilizada en la práctica para estimar las características del movimiento del terreno en zonas de alta sismicidad. En este sentido, las fuerzas sísmicas de diseño delineadas en la mayoría de las normativas actuales de diseño (como ASCE-07, EUROCODE 9, IBC, entre otras) se basan en un APPS.

Este artículo presenta los resultados de un APPS para un sitio localizado en el centro de la ciudad de Santiago (República Dominicana). Santiago es una ciudad con alta densidad poblacional (segunda ciudad más grande de la República Dominicana) localizada en la región norte de la isla La Española. El sitio de interés y las fallas sísmicas activas de La Española se muestran en la figura 1, donde “SFZ” denota la falla Septentrional. La falla Septentrional es la falla sísmica activa más importante de la República Dominicana y no ha sufrido una ruptura significativa en un gran segmento de la falla en más de 500 años (una pequeña porción sufrió una ruptura en 1950). Dadas las características del medio construido de la ciudad de Santiago y su cercanía a la falla Septentrional, el sitio de interés puede ser considerado como la localidad de mayor riesgo sísmico del país.

Investigaciones recientes sugieren que la falla Septentrional se puede encontrar en la última fase de su ciclo de ruptura (Calais et al., 2002), y por esta razón es de interés caracterizar el posible movimiento del suelo que pudiera generar en las localidades cercanas. Este artículo presenta los resultados de un APPS realizado, tomando en cuenta datos sismológicos recientes, tales como tasa de deslizamiento de la falla estimada usando un sistema de posicionamiento global (Calais et al., 2002; Frankel, Harmsen, Mueller, Calais, & Haase, 2010). Las características del movimiento del terreno estimadas incluyen aceleración máxima del terreno (AMT) y el espectro de pseudo-aceleración para razón de amortiguamiento de 5 %.

El resto del artículo está organizado de la siguiente manera. En la siguiente sección las fuentes de peligrosidad sísmica son discutidas brevemente, seguido de la descripción del modelo de recurrencia de terremotos adoptado. Luego, se presentan las curvas de excedencia para varios periodos de exposición; las curvas de exposición son usadas como base para la estimación de parámetros de intensidad de movimientos del terreno para varias probabilidades de excedencia. Finalmente, es estudiado el efecto de la ubicación de la zona de ruptura en la falla, seguido de conclusiones y comentarios.

2. Fuentes de peligrosidad sísmica (fallas sísmicas)

La ciudad de Santiago se encuentra localizada en la región norte de la isla La Española, delimitada por la falla Septentrional al norte y la falla de La Española al sur (ver figura 1). Basado en mediciones de la deformación de la falla, obtenidas mediante un sistema de posicionamiento global, el peligro sísmico en Santiago se encuentra dominado por la falla Septentrional (Calais et al., 2002). Por esta razón, en este artículo solo se considera la falla Septentrional como fuente de terremotos.

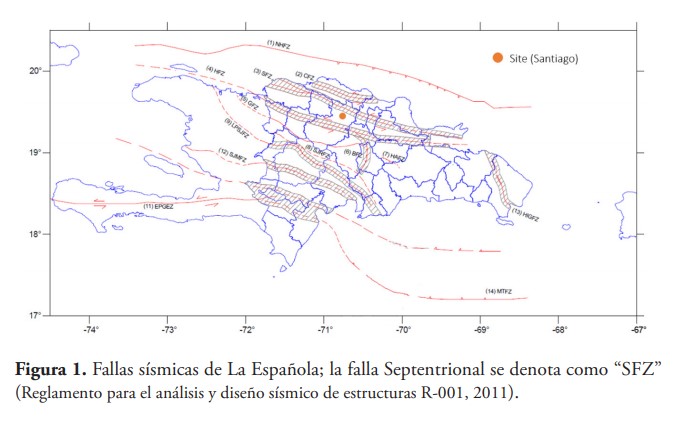
La falla Septentrional es una falla de desplazamiento horizontal (transformante o de desgarre) que cruza la región norte de La Española y acomoda parte del movimiento entre las placas de Norte América y el Caribe; cabe recalcar que este movimiento entre dichas placas ocasionó el devastador terremoto de Haití en el 2010. Trincheras excavadas en la zona y pruebas con radiocarbono mostraron que la falla ha acumulado al menos 5 m de deformación, y que la ruptura de superficie más severa en la porción central de la falla (zona más cercana a Santiago) ocurrió en el año 1260 (Mann, Prentice, Burr, Peña & Taylor, 1998). A pesar de que una pequeña porción de la energía de deformación acumulada fue liberada en los terremotos de 1562, 1776, 1783 y 1842, el consenso es que el periodo de retorno del terremoto característico de esta falla ha sido excedido (Frankel, Harmsen, Mueller, Calais & Haase, 2010; Isidro et al., 2017). La razón de deslizamiento de la falla se estima en 12 mm/año, y la magnitud característica o máxima magnitud de ruptura se estima en 7.8 (Calais et al., 2002; Frankel et al., 2010).

3. Modelo de Magnitud-Recurrencia

El potencial de una falla para generar terremotos fuertes puede ser parcialmente cuantificado usando la razón anual media de excedencia λm definida como la razón entre el número de terremotos de magnitud (momento) mayores que m, dividido entre el intervalo de tiempo considerado. Usando información de las razones de deslizamiento de fallas y sismicidad histórica y medida con instrumentos, las razones anuales medias de excedencia para la falla Septentrional y terremotos de magnitud m=6.5 y m=7 son (Frankel et al., 2010)

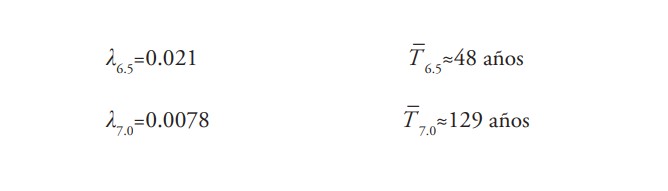
donde T _ denota el periodo de retorno o intervalo de recurrencia media. Tradicionalmente, la ecuación de Gutenberg-Richter (GR) es utilizada para relacionar magnitud y recurrencia de terremotos en una región. En este modelo la relación entre razón anual (media) de excedencia y magnitud está dada por

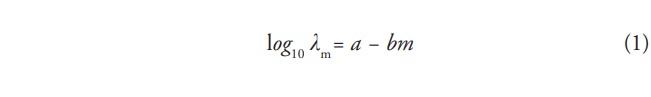
donde a y b son parámetros del modelo, y m es la magnitud (momento) de terremoto considerada. Usando las razones de excedencia estimadas en Frankel et al., (2010), el modelo GR calibrado tiene como parámetros a = 3.91 y b = 0.86 para la falla Septentrional. El modelo de Gutenberg-Richter implica que la distribución de probabilidad de la magnitud de terremoto en el sitio es exponencial.

El modelo de Gutenberg-Richter no tiene límite superior y estima razones de excedencia mayores a las observadas en la práctica para terremotos grandes (magnitud aproximadamente mayor de 7). El modelo GR puede ser modificado para incluir un límite inferior y un límite superior para delimitar la magnitud a un rango de interés. En el modelo GR con límite la razón anual de excedencia está dada por (Youngs & Coppersmith, 1985)

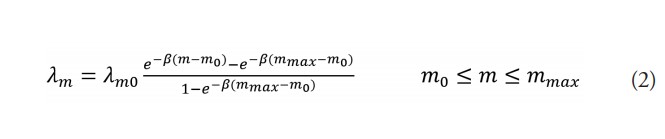
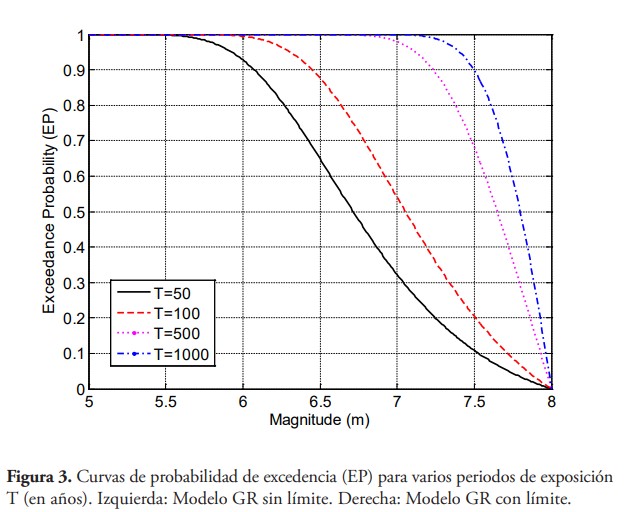
Lo que resulta en un modelo de probabilidad exponencial truncado para la magnitud de terremotos en el sitio. Para calibrar el modelo GR con límite para la falla Septentrional la magnitud máxima se seleccionó como mmax=8, basado en resultados obtenidos en Frankel et al., (2010), mientras que la magnitud mínima se seleccionó como m0 =5. Usando las razones de excedencia discutidas anteriormente, los parámetros del modelo GR con límite para la falla Septentrional son β=1.75 y λm0=0.31 La figura 2 muestra una comparación de las razones de excedencia estimadas con los dos modelos de recurrencia (modelo GR sin y con límite). Como puede observarse, el modelo GR sin límite predice razones de excedencia significativamente mayores que el modelo con límite para magnitudes mayores de 7.5; la figura también muestra el periodo de retorno (intervalo de recurrencia media) estimado por ambos modelos. El modelo GR con límite es adoptado en este artículo para caracterizar la relación entre magnitud y recurrencia de terremotos.

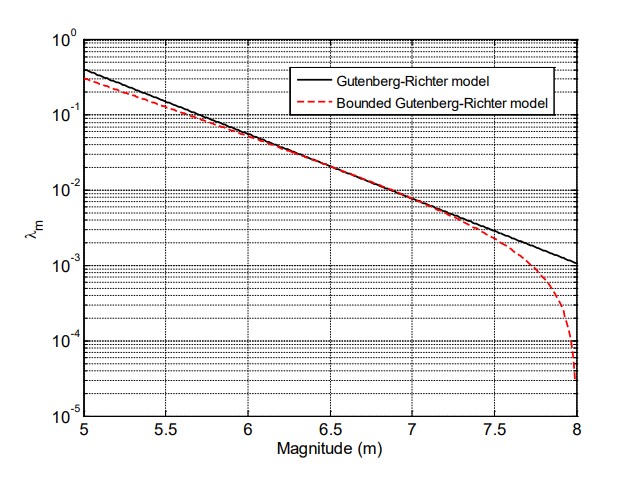
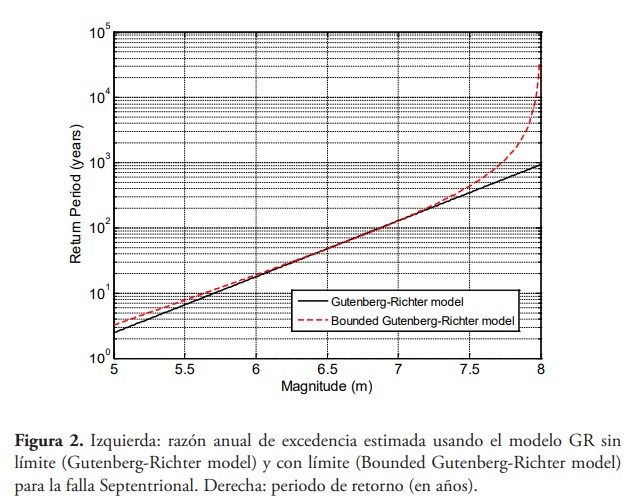
4. Curvas de excedencia de magnitud en un intervalo de tiempo

Los modelos de magnitud-recurrencia discutidos en la sección anterior permiten estimar la distribución de probabilidad de la magnitud de terremotos esperados en el sitio y la razón de excedencia en cualquier tiempo, es decir, el intervalo de tiempo no tiene límite. En otras palabras, los modelos permiten caracterizar la ocurrencia de terremotos en el espacio. Para aplicaciones en ingeniería también es de interés caracterizar la potencial ocurrencia de terremotos en un intervalo de tiempo relacionado a la vida útil de una estructura (por ejemplo, 50 años, 100 años, 500 años, etc.), es decir, una caracterización temporal de la ocurrencia de terremotos. Una vez definida la vida útil o el tiempo de vida de la estructura, el objetivo es estimar la probabilidad de exceder parámetros relacionados al movimiento del terreno (típicamente aceleración máxima del terreno o espectros de respuesta) para diseñar estructuras para valores de dichos parámetros con “pequeña” probabilidad de ser excedidos en dicho intervalo.

Definir un intervalo de tiempo para la vida útil de una estructura (también conocido como tiempo de exposición) implica que un modelo de la ocurrencia de terremotos en el tiempo es necesario. El proceso de Poisson es generalmente utilizado para modelar la ocurrencia en el tiempo de eventos relacionados a la ocurrencia de terremotos. En dicho modelo el número de ocurrencias XT de un evento en un intervalo de tiempo [0,T] es modelado como una variable aleatoria con distribución de probabilidad:

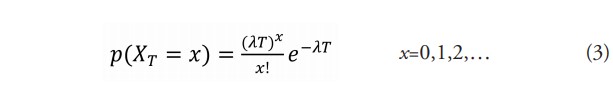
donde λ es la razón anual media de ocurrencia del evento XT y T es el intervalo de tiempo en años. La media y la varianza de la variable aleatoria XT es λT. El evento XT puede ser, por ejemplo, el número de terremotos que exceden una cierta magnitud, o el número de veces que un parámetro de respuesta (como aceleración máxima del terreno u ordenadas del espectro de respuesta de pseudo-aceleración) exceden cierto valor. La probabilidad de excedencia (EP) es definida como la probabilidad de que el evento XT ocurre al menos una vez en el intervalo de tiempo considerado, y está dada por

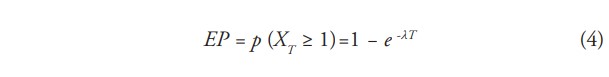
El período de retorno de un evento con probabilidad de excedencia EP está dado por 

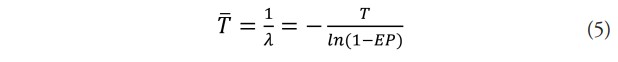
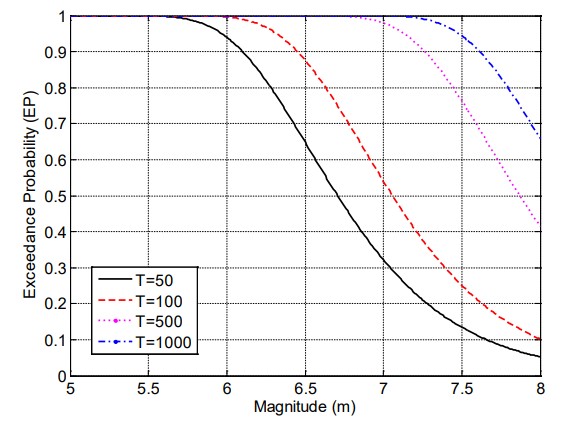
La probabilidad de excedencia para la magnitud de terremoto se muestra en la figura 3 para varios tiempos de exposición y razones anuales estimadas tanto el modelo GR sin límite como con el modelo GR con límite; curvas de este tipo se conocen como curvas de peligro sísmico. Como puede observarse, para magnitudes mayor de 7 las probabilidades de excedencia estimadas con el modelo sin límite son significativamente más altas que las estimadas con el modelo con límite.

Basado en el modelo con límite, un terremoto de magnitud m=7.9 tiene una probabilidad de excedencia de 2 % en 50 años (periodo de retorno de 2475 años), mientras que un terremoto de magnitud m=7.5 tiene una probabilidad de excedencia de 10 % en 50 años (periodo de retorno de 475 años). El terremoto característico de la falla Septentrional tiene una magnitud estimada de 7.8 (Frankel et al., 2010), y de acuerdo al modelo con límite el mismo posee una probabilidad de excedencia de 3.3 % en 50 años o un periodo de retorno de 1460 años.

Es importante resaltar que el modelar la ocurrencia de terremotos (y eventos relacionados a la misma) como un proceso de Poisson contradice los procesos físicos que generan los terremotos y la teoría de rebote elástico, generalmente adoptada para explicar este fenómeno natural, debido a que asume que las ocurrencias de terremotos generados en una falla son eventos independientes. Dados los mecanismos de acumulación y liberación de energía de deformación que tienen lugar en fallas sísmicas, existe una alta correlación temporal entre terremotos consecutivos. Esto implica que la razón de ocurrencia media es dependiente del tiempo, un comportamiento que puede modelarse usando la ley de potencia de Omori (Omori, 1895; Utsu, Ogata & Matsuura, 1995).

A pesar de que algunos investigadores argumentan que la discrepancia entre modelos físicos y estadísticos que describen la ocurrencia de terremotos son suficientes para que el APPS sea inválido para predecir/estimar las características de terremotos (Mulargia, Stark & Geller, 2017), estudios recientes han probado que los resultados del APPS muestran cierta consistencia con observaciones empíricas (Kammerer and Ake, 2012). Además, modelos recientes de la ocurrencia de terremotos buscan tomar en consideración la dependencia en el tiempo del comportamiento, lo cual es una de las limitaciones principales del APPS (HERP, 2010).

5. Parámetros del movimiento del terreno en el sitio

La experiencia ha demostrado que las características de movimientos del terreno inducidos por terremotos varían, significativamente, tanto para distintos sitios como para diferentes terremotos. En adición, las características del movimiento del terreno que tienen mayor impacto en la respuesta y el comportamiento de estructuras son amplitud (intensidad), duración y contenido de frecuencia. Los principales factores que afectan estos parámetros del movimiento del suelo son:

• Tipo de falla, profundidad de la zona de ruptura, orientación de la falla.
• Magnitud del terremoto, que a su vez depende del área de la zona de ruptura, el desplazamiento de la falla, y el módulo de corte de la roca adyacente a la falla.
• Características del medio de propagación, propiedades locales del suelo y topografía.

Dada la dificultad de cuantificar de manera directa el impacto de todos estos factores en el movimiento del terreno usando modelos analíticos (basados en conceptos físicos/mecánicos), modelos empíricos conocidos como leyes de atenuación, son desarrollados usando análisis de regresión y datos de sismicidad pasada, para estimar las características del movimiento del suelo y su efecto en el comportamiento de estructuras. Cuando hay suficiente data disponible se puede obtener una ley de atenuación para el sitio específico de interés. Sin embargo, generalmente este no es el caso, y debe adoptarse una ley de atenuación de la literatura existente, basada en datos de distintos sitios con condiciones similares (principalmente tipo de falla) a las del sitio de interés.

Dada la escasez de datos de eventos telúricos relacionados a la falla Septentrional (y a la República Dominicana en general) la ley de atenuación propuesta por Campbell para terremotos superficiales en la corteza terrestre es adoptada en este artículo. Los parámetros del movimiento del suelo de interés incluyen aceleración (horizontal) máxima del terreno y espectro de respuesta de pseudo-aceleración para razón de amortiguamiento de 5 %. La ley de atenuación de Campbell se basa en datos de terremotos superficiales de todo el mundo con magnitudes entre 4.7 y 8.1 medidos en estaciones en lugares sobre depósitos con al menos 10 m de suelo firme o roca suave/dura (Campbell, 1997).

Los parámetros usados en el modelo de Campbell para estimar características del movimiento del terreno en el sitio son:

r = distancia más corta a la falla (distancia sismogénica) = 8 km

D = profundidad a roca firme = 3 km

F = factor de falla sísmica = 0 (falla lateral)

S_SR = factor de tipo de suelo = 0 (suelo firme)

S_HR = factor de tipo de suelo = 0 (suelo firme)

La distancia sismogénica de 8 km se basó en un sitio en el centro de la ciudad de Santiago, mientras que la profundidad a la roca firme se basó en resultados de estudios geotécnicos realizados anteriormente. Los parámetros de suelo se seleccionaron como suelo firme, debido a que es el que predomina en el área; este parámetro se debe ajustar para otros tipos de suelo.

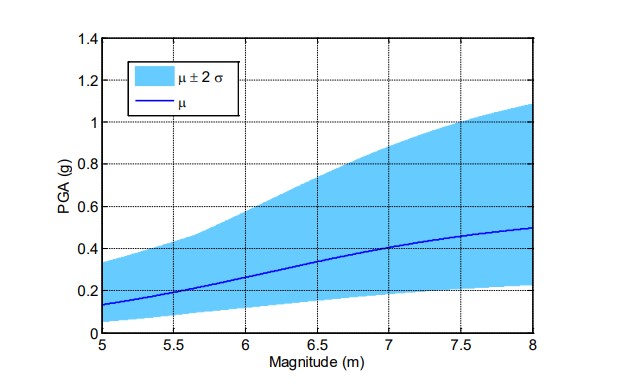
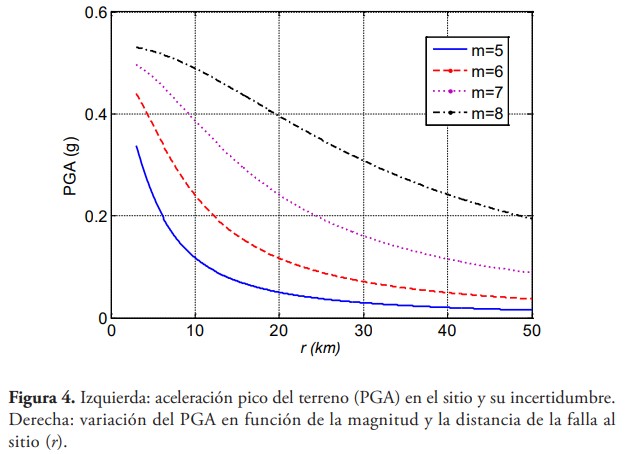
Con los datos mencionados anteriormente, la aceleración máxima del terreno (PGA) en el sitio, estimada con la ley de Campbell, se muestra en la figura 4. La figura muestra la incertidumbre en el PGA caracterizada por dos desviaciones estándar; como el PGA se modela como una variable aleatoria lognormal, la incertidumbre se representa como la desviación estándar de la variable normal asociada. La incertidumbre mostrada es la incertidumbre asociada a la ley de atenuación. El panel derecho de la figura 4 ilustra la variación del PGA en función de la magnitud y la distancia.

Cabe recalcar que la distancia r es la distancia más corta del sitio a la zona de potencial ruptura (distancia sismogénica) en la falla. Sin embargo, una ruptura puede ocurrir a lo largo de la falla, no necesariamente en el punto más cercano al sitio. El efecto de la ubicación de la zona de ruptura en la falla se considerará más adelante en este artículo.

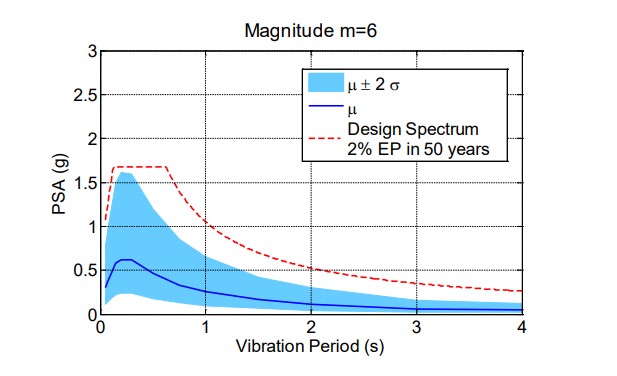
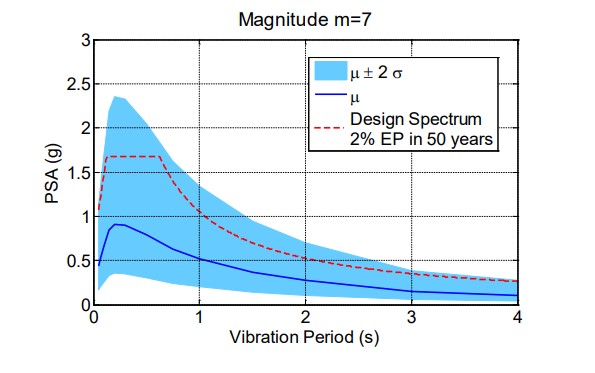
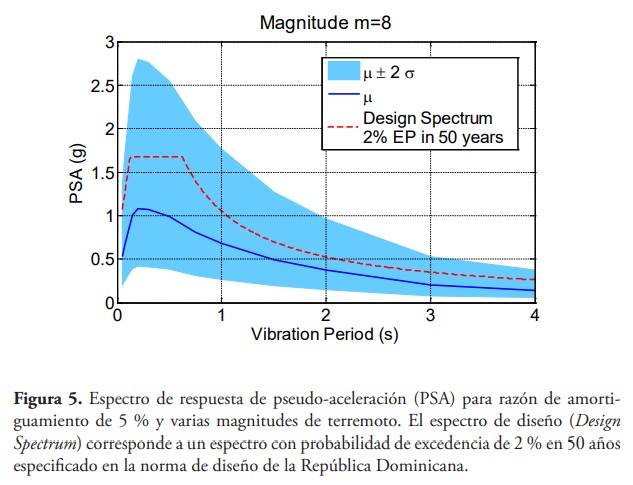
La estimación del espectro de respuesta de pseudo-aceleración espectral (PSA) con 5 % de razón de amortiguamiento se muestra en la figura 5 para varias magnitudes de terremoto; la incertidumbre dada por dos desviaciones estándar se muestra en la figura, donde las ordenadas espectrales son variables lognormal y la media y la varianza mostrada corresponden a la distribución normal asociada. Para fines de comparación también se muestra en la figura el espectro de diseño con probabilidad de excedencia de 2 % en 50 años para suelo firme especificado en la norma de diseño de la República Dominicana para el sitio de interés.

5.1 Curvas de excedencia de parámetros del movimiento del terreno

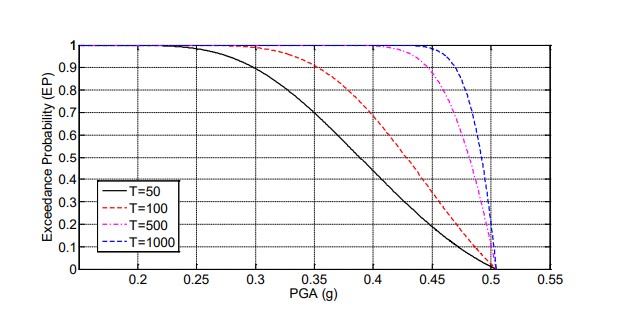
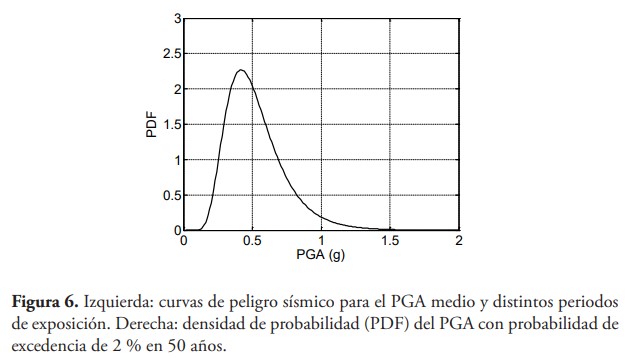
Las curvas de probabilidad de excedencia (curvas de peligro sísmico) para diferentes parámetros del movimiento del terreno de interés en ingeniería sísmica se muestran a continuación. Las curvas de peligro sísmico se calcularon usando la ley de atenuación de Campbell y el modelo de GR con límite, discutidos en secciones anteriores. El panel izquierdo de la figura 6 muestra la probabilidad de excedencia de la aceleración máxima del terreno (PGA) media para varios periodos de exposición. Los valores del PGA con probabilidades de excedencia de 2 % y 10 % en 50 años son, respectivamente, 0.49 g y 0.47 g. El panel derecho de la figura 6 muestra la función de densidad de probabilidad (PDF) del PGA con probabilidad de excedencia de 2 % en 50 años, modelado como una distribución lognormal. La incertidumbre mostrada en la figura 6 se relaciona con la ley de atenuación de Campbell, es decir, a la variabilidad inherente de la respuesta medida en un sitio debido al tipo de falla y mecanismos de ruptura, propiedades del medio de propagación, propiedades locales del terreno, entre otras. Basado en esta PDF hay una probabilidad de 3.6 % de que el PGA con probabilidad de excedencia de 2 % en 50 años sea mayor de 1 g.

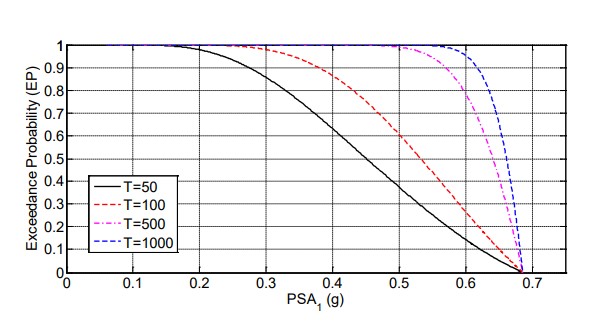
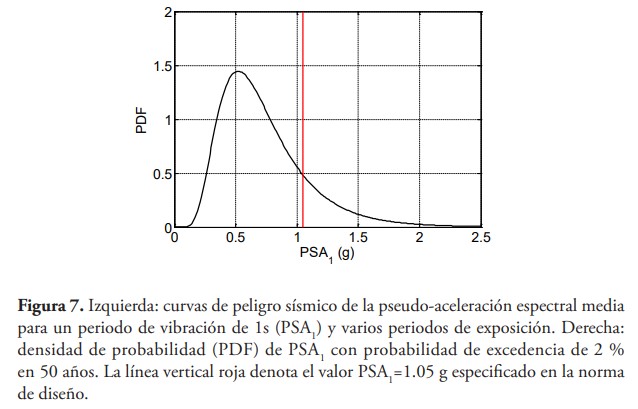
El panel izquierdo de la figura 7 muestra las curvas de peligro sísmico de la pseudo-aceleración espectral (con 5 % de amortiguamiento) para un período de vibración de 1s (PSA1 ) y varios periodos de exposición; esta variable, generalmente, se denota como S1 en las normas de diseño y es usada para construir los espectros de diseño. La media de PSA1 con probabilidades de excedencia de 2 % y 10 % para un periodo de retorno de 50 años son, respectivamente, 0.65 g y 0.62 g. El panel derecho de la figura 7 muestra la función de densidad de probabilidad (PDF) del PSA1 con probabilidad de excedencia de 2 % en 50 años. La incertidumbre dada por la PDF se debe a la ley de atenuación; basado en este modelo existe una probabilidad de 17 % de exceder el valor de 1.05 g especificado en la norma de diseño.

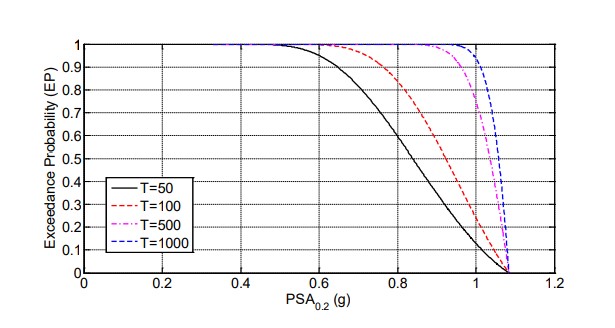
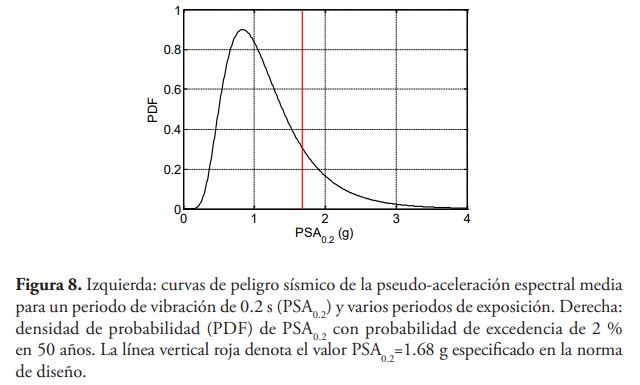
El panel izquierdo de la figura 8 muestra las curvas de peligro sísmico de la pseudo-aceleración espectral (con 5 % de amortiguamiento) para un periodo de vibración de 0.2 s (PSA0.2) y varios períodos de exposición; un valor cercano a esta cantidad generalmente se denota como Ss en las normas de diseño y es usada para construir los espectros de diseño. La media de PSA0.2 con probabilidades de excedencia de 2 % y 10 % para un periodo de retorno de 50 años son, respectivamente, 1.07 g y 1.01 g. El panel derecho de la figura 8 muestra la función de densidad de probabilidad (PDF) del PSA0.2 con probabilidad de excedencia de 2 % en 50 años. La incertidumbre dada por la PDF se debe a la ley de atenuación; basado en este modelo existe una probabilidad de 17 % de exceder el valor de 1.68 g especificado en la norma de diseño.

5.2 Efecto de la ubicación de la zona de ruptura

Los resultados mostrados anteriormente se obtuvieron asumiendo que la zona de ruptura se encuentra en el punto más cerca al sitio, es decir, se utilizó la distancia sismogénica definida como la distancia más corta de la falla al sitio. Sin embargo, la zona de ruptura en una falla se puede ubicar en cualquier zona activa a lo largo de la falla. En esta sección, se considera la ubicación de la zona de ruptura como una variable aleatoria uniforme a lo largo de la falla con una distancia máxima de 25 km, medida desde la ubicación del punto de la distancia sismogénica (más corta) a lo largo de la falla.

Con este fin se realizó un análisis de Monte Carlo para estimar la densidad de probabilidad (PDF) de los parámetros de respuesta discutidos anteriormente. En este caso la distancia r del sitio a la zona de ruptura está dada por

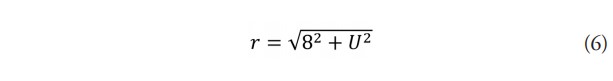
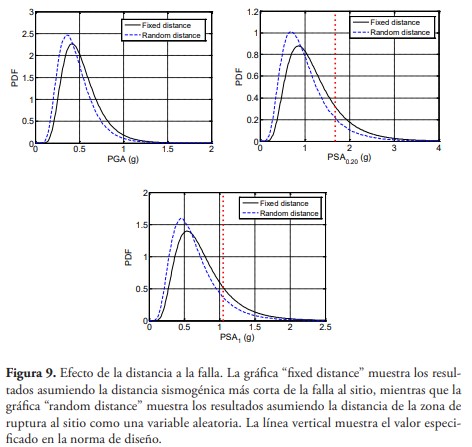
donde es una variable aleatoria uniforme U(-25,25) en el rango [-25 km, 25 km]. Para realizar el análisis de Monte Carlo se utilizaron 300,000 números aleatorios; se observó convergencia de los resultados con dicha muestra. La figura 9 presenta la comparación de los resultados de la estimación de PGA, PSA1 y PSA0.20 tanto asumiendo la distancia más corta como la distancia a lo largo de la falla. Como es de esperarse, las distribuciones obtenidas considerando la zona de ruptura a lo largo de la falla muestran un desplazamiento a la izquierda con respecto a las distribuciones obtenidas, asumiendo la distancia más corta. Para fines de comparación, la línea vertical muestra el valor especificado en la norma de diseño.

6. Conclusiones

Este artículo presentó los resultados de un análisis probabilístico de peligro sísmico (APPS) realizado para un sitio en el centro de la ciudad de Santiago (República Dominicana). Para realizar el análisis se utilizaron datos recientes de la sismicidad de la falla Septentrional para calibrar un modelo de recurrencia de Gutenberg-Richter con límite. El modelo calibrado se utilizó junto a la ley de atenuación de Campbell para estimar las curvas de peligro sísmico de distintos parámetros como magnitud de terremoto, aceleración máxima del terreno, y ordenadas del espectro de respuesta de pseudo-aceleración para razón de amortiguamiento de 5 %. Los resultados del APPS se compararon con el espectro de respuesta de diseño con probabilidad de excedencia de 2 % en 50 años especificado en la normativa de la República Dominicana. Se encontró que existe una probabilidad de 17 % de que las ordenadas espectrales excedan las especificadas en la norma de diseño debido a incertidumbres relacionadas a la ley de atenuación empleada en el análisis. Basado en el modelo de atenuación el espectro de diseño es consistente con los espectros generados por terremotos de magnitud momento de 7.9, valor que es cercano al terremoto característico de la falla Septentrional estimado en 7.8 en estudios recientes.

Reconocimientos

Esta investigación fue parcialmente apoyada por el proyecto de investigación del Instituto Tecnológico de Santo Domingo (INTEC) y del Ministerio de Educación Superior Ciencia y Tecnología (MESCYT) a través del programa FONDOCYT. El autor agradece el soporte de ambas instituciones para materializar esta investigación.