Validación de un método heurístico de optimización basado en un sistema de infección por virus

1. Introducción

Los problemas de optimización existen en cualquier tarea que involucre la búsqueda de una solución, es decir, la que maximice o minimice el rendimiento de una operación o función, dentro de un espacio de soluciones que cumplen con ciertas restricciones (López, 2015). Para resolver este tipo de problemas se han propuesto muchas técnicas, entre las más tradicionales se encuentra el cálculo de la deriva, estas se aplican cuando las funciones que se desean evaluar tienen características lineales, como determinar el área mínima de un cuadrado dada ciertas restricciones de tamaño. También se encuentra el método del gradiente utilizado cuando las funciones son no lineales, como buscar el mínimo en una curva de demanda-precios.

Sin embargo, existen otros tipos de problemas de optimización que no pueden ser resueltos por los métodos tradicionales, debido a que poseen variables con valores discretos. Esto aumenta la complejidad del cálculo y los métodos tradicionales son incapaces de producir soluciones óptimas (Xinjie y Mitsuo 2010). Un ejemplo de este tipo de problemas es encontrar la mejor ruta de tránsito de un punto a otro en una ciudad. Para resolver este tipo de problemas se han propuesto diferentes algoritmos basados en procesos naturales, siendo el más utilizado el Algoritmo Genético (GA), el cual utiliza la selección natural (supervivencia del más apto) y los principios de la genética (Carson, 2017). Estos algoritmos van creando soluciones y dichas soluciones van evolucionando a través de operaciones de selección, cruce y mutación, similares a la evolución genética natural, con el objetivo de buscar valores óptimos del problema.

Otros algoritmos de optimización parten de la misma idea y simulan otros procesos naturales, tales como los algoritmos de partículas (Particle Swarm) utilizados para resolver problemas de optimización de gran escala y no lineales, como el descrito en Del Valle, Kumar, Mohagheghi, Hernandez y Harley (2007), donde se plantea la optimización de varias etapas del sistema de distribución eléctrico teniendo en cuenta restricciones operacionales y de diseño complejas. Este algoritmo está basado en el comportamiento social de grupos de organismos tales como manadas, bandadas de pájaros, peces, hormigas, etc. Estos organismos llamados partículas van tomando información de su propia experiencia de movimiento y de sus vecinos para encontrar la mejor solución del problema (Tong, Dong, Ai, y Jing, 2018).

Este artículo presenta la implementación de un algoritmo de optimización basado en el proceso de infección de un organismo por un virus; es un proceso natural que puede ser usado para realizar un potente algoritmo de optimización. Se han realizado algunos trabajos que tienen esta idea general, como el propuesto por Bey, Bouzand, Benhammadi, y Nacer (2019) que presenta una combinación de un sistema de infección por virus mezclado con un algoritmo genético para optimizar el proceso de asignación de tareas a las máquinas virtuales en diferentes servidores en un ambiente en la nube. 

En esta investigación se toma la propuesta de Cortés, García, Onieva, Muñuzuri, y Guadix (2008),quienes presentan un más completo, tomando todos los elementos y procesos presentes durante la infección para adaptarlo a un algoritmo cuyo objetivo principal es infectar las células del organismo que representan posibles soluciones, en búsqueda de las más resistentes al virus luego dela infección, que sería la solución óptima del problema. El objetivo principal de esta propuesta es la implementación de forma práctica el algoritmo propuesto utilizando la herramienta computacional Matlab y llevar a cabo pruebas con diferentes problemas de optimización de complejidad simple y mediana, y de esta forma comprobar su funcionamiento y eficiencia comparados con otros algoritmos conocidos.

Para lograr el objetivo antes mencionado, primero se hace una revisión de la literatura propuesta donde se explica la base biológica del algoritmo, los componentes y las fases que intervienen en un proceso de infección de un virus a un organismo. Esto dará pie a una correcta aplicación y orientación del algoritmo. En la siguiente parte se realiza la aplicación de la analogía detallando cómo se representa cada elemento al problema de optimización y cuál es la estructura del algoritmo. Finalmente, se presentan los resultados obtenidos luego de realizar las pruebas con dos tipos de funciones, función Onemax de complejidad simple, que ayuda a comprobar el funcionamiento básico del algoritmo y la función Engañosa (Deceptive Function) de complejidad mediana, que pone a prueba la capacidad de convergencia del algoritmo ante condiciones “engañosas”.

2. Descripción del sistema de virus (VS)

2.1 Descripción de la analogía

Los virus son organismos acelulares que se caracterizan por su pequeño tamaño, estructura muy elemental y especial mecanismo de replicación. Son parásitos intracelulares obligados y solo se desarrollan en el interior de células vivas, de las que dependen para obtención de energía y síntesis de proteínas (Mahy, 2001). 

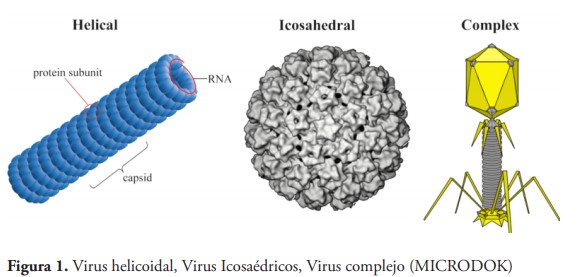
Los virus están constituidos por una molécula de ácido nucleico ADN o ARN, rodeada por una capa de proteínas llamada cápside. Al complejo ácido nucleico-cápside se le denomina nucleocápsida. La figura 1 muestra los diferentes tipos de virus, estas formas dependen de la unión de los capsómeros. Los virus complejos como los bacteriófagos son resultado de combinar diferentes estructuras (Loeffelholz, Hodinka, Pinsky y Young, 2016). La acción patógena de los virus es multifactorial, y depende de factores del virus y del huésped, como la capacidad de penetración, multiplicación e invasión del virus, la interferencia con los mecanismos naturales de defensa y la capacidad para lesionar células y tejidos.

A lo largo de este artículo se toma como referencia el comportamiento de los bacteriófagos o fagos, que son organismos que infectan a las bacterias. La característica principal de este tipo de organismo es la forma en que se adhiere a la bacteria, primero, fijándose con las colas a la membrana externa, luego el ADN vírico viaja desde la cabeza a través de la vaina y se inyecta a la bacteria utilizando las espículas (Harrington, 2017). La figura 2 muestra las partes principales que componen los fagos.

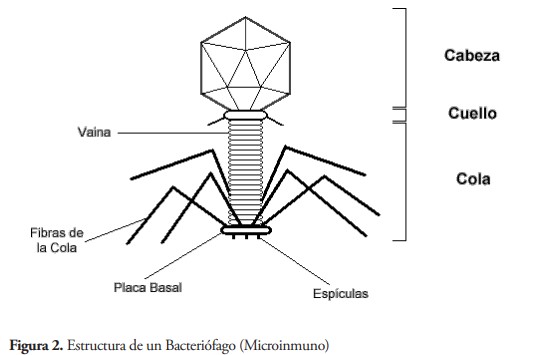
La producción de nuevas partículas virales es el único objetivo de los virus, dado que son formas acelulares e inanimadas en estado extracelular. La multiplicación vírica es un complejo proceso que se divide en varias fases:

Absorción y penetración: es el proceso por medio del cual el virus se une a la célula hospedadora. Cualquier virus no puede unirse a cualquier célula, pueden unirse a un tipo de célula en concreto y depende de su estado de salud. Tras la absorción el virus penetra inyectando ácido nucleico al interior del hospedador. 

Síntesis y ensamblaje: durante este proceso se replica el ácido nucleico inyectado por el virus. Una vez fabricados todos los componentes víricos se inicia la producción de los viriones, es decir, la formación completa de los virus dentro del huésped.

Liberación: las partículas víricas formadas salen de la célula rompiendo las membranas celulares para iniciar el proceso de infección de otras bacterias.

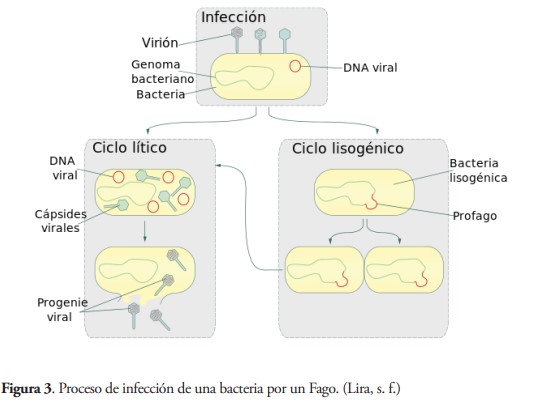
El ciclo de multiplicación, que termina con lisis celular, recibe el nombre de Ciclo Lítico (figura 3), y los virus que los llevan a cabo son virus virulentos. Pero existen otros virus capaces de permanecer en estado latente en la célula que parasitan, gracias a la integración del ADN vírico en el ADN celular; en este caso se llama Ciclo Lisogénico (figura 3), durante este tipo de ciclo se puede conferir características que antes no tenía la bacteria (mutación). Este huésped infectado llamado profago se replicará cada vez que lo haga el genoma bacteriano. El ciclo lisogénico puede convertirse en lítico debido a algún tipo de acción externa para luego iniciar una reproducción de nucleocápcidas en el interior de la bacteria. La difteria es un ejemplo de virus que realiza un proceso lisogénico para luego convertirse en lítico (Miskevich, 2016).

2.1.2 Mecanismos de defensa

Existe una respuesta inmunitaria específica frente a las infecciones virales (humoral y defensa celular). La respuesta de tipo humoral es llevada a cabo por los anticuerpos externos. El mecanismo de defensa más importante es la inmunidad celular, que es capaz de inhibir la patógena de la infección viral. Esto da como resultado una respuesta inmune natural que parte desde la propia bacteria, haciendo uso de las habilidades y condiciones de salud de la misma. Esto permite dar una respuesta contra los agentes infecciosos que no se está inmunizado, retardando de esta manera el proceso del virus o impidiendo su infección.

2.2 Descripción sistema de optimización por infección de virus (VS)

Un problema general de optimización se puede definir como la búsqueda de la mejor solución x que maximiza o minimiza una función objetivo f(x); este conjunto de soluciones g se encuentra dentro de ciertos parámetros o restricciones que posee el problema de manera particular.

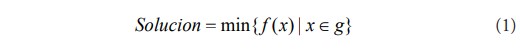
El VS se enfoca en la capacidad que tienen los de fagos de infectar bacterias; estas bacterias infectadas entran a formar parte de un grupo de posibles soluciones del problema de optimización. El objetivo se cumple cuando el organismo logra aislar el virus con las bacterias más resistentes a la reproducción del virus, es decir, se ha encontrado una solución óptima dentro del conjunto de bacterias infectadas.

Este sistema de virus descrito por Cortés et al., (2008) está definido por tres componentes principales que son un conjunto de virus, un organismo y la interacción entre ellos.

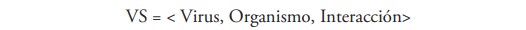
2.2.1 Virus

El conjunto de virus del VS se representa:

Cada virus simple se define por 4 componentes:

Estado_i : define la bacteria infectada por el virus. Es la codificación de la solución matemática en términos computacionales, que también se llama genoma.

Cuando un virus infecta una bacteria, el tiempo de residencia y reproducción del virus dentro del hospedador se define por el número de nucleocápsidas que se replican en el ciclo lítico (NR) o el número de iteraciones en el ciclo lisogénico (IT). El estado_i del virusi se define:

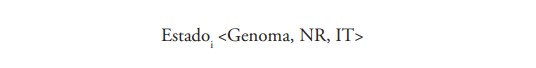
Entrada_i : es la información que el virus busca del organismo, esta información siempre es recolectada en las inmediaciones de la bacteria infectada por el virus. Entrada_i representa la interacción de la información del organismo  virus. Esto corresponde al vecindario de la bacteria infectada en términos computacionales.

Salida_i : identifica la acción que el virus puede tomar. La Salida_i es la interacción virus > organismo. Esto es, la elección del tipo de ciclo de reproducción que se llevará a cabo en el proceso de infección.

Proceso_i : representa el comportamiento autónomo del virus, cambiando el Estado_i . Se corresponde con proceso en el que se desarrolla el tipo de replicación durante la infección, lítico o lisogénico.

2.2.2 Organismo

El organismo del VS está definido por dos componentes: 

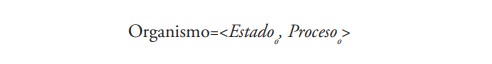
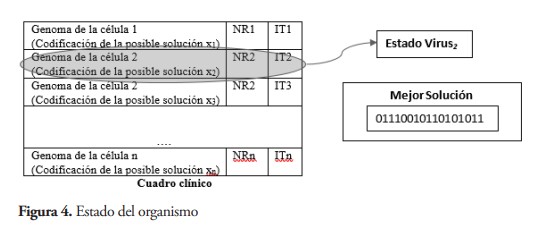
Estado_o : representa el estado del organismo en cada momento. Consiste en el cuadro clínico donde se encuentra la población de las bacterias que han sido infectadas (las mejores soluciones encontradas en el problema de optimización). El conjunto de posibles soluciones en el cuadro clínico debe cumplir con las restricciones impuestas por cada problema de forma particular.

El Cuadro Clínico está compuesto por las tuplas que definen el Estado_i de las bacterias infectadas, Genoma-NR-IT. En este cuadro se encuentra toda la información relativa a las bacterias infectadas necesaria para el algoritmo en cada instante de tiempo. El Estadoo del organismo está representado por el cuadro clínico y la mejor solución encontrada. La figura 4 presenta la matriz que contiene el genoma con la codificación de cada una de las bacterias y sus respectivos valores LNR y LIT para los diferentes tipos de reproducción.

Proceso_o : representa la forma que el organismo tiene para protegerse de la infección del virus, consiste en una producción de anticuerpos en las bacterias que provoca una respuesta inmunológica que la protege de ser infectada.

2.2.3 Interacción del virus y el organismo

El proceso de búsqueda de soluciones inicia cuando se produce un ataque del virus; el virus trata de encontrar las bacterias con menor salud (proceso del virus) para infectarla, y el organismo produce anticuerpos para defenderse de los ataques del virus (proceso del organismo). El resultado de la iteración provoca un cambio general en el estado del organismo con nuevas bacterias infectadas que representan mejor solución de encontradas hasta el momento.

2.2.3.1 Proceso de interacción del virus con el organismo

Entrada: es el proceso de elegir el vecindario correspondiente a las bacterias infectadas, de esta forma se busca posibles soluciones con mejores resultados que se encuentren dentro de los parámetros establecidos por las restricciones. Este conjunto de posibles soluciones se llama vecindario de las posibles soluciones. Las características y la elección de cada uno de sus miembros dependen del problema a optimizar.

Salida: es el proceso de elección del tipo de reproducción con que el virus se desarrollará en la bacteria infectada. La reproducción puede ser de dos tipos: lítica con probabilidad P_ly o lisogénica con probabilidad P_li, la sumatoria de estas dos probabilidades debe ser 1 debido a que el virus puede desarrollarse de una sola forma dentro del hospedador.

2.2.3.2 Proceso de reproducción lítico

El proceso de reproducción lítico se puede llevar a cabo de dos formas, dependiendo el tipo de analogía biológica que se desee representar. El virus puede atacar el organismo de forma invasiva y masiva infectando varias bacterias en un solo ciclo (Cortés, García, Muñuzuri, y Guadix, 2012) o puede seleccionar solo la bacteria que tenga menor salud del vecindario. En el caso de este artículo se desarrolla el método de infección selectiva.

La reproducción lítica selectiva en donde las bacterias infectadas que han desarrollado nucleocápsidas liberan nuevos fagos que van en búsqueda de nuevas bacterias para infectar e incluir en un cuadro clínico donde se almacenan las posibles soluciones. Cada fago evalúa el vecindario y selecciona la más débil para incluirla en el cuadro clínico.

La producción de nucleocápsidas se produce en cada iteración, donde cada bacteria infectada que representa una posible solución, es evaluada con una función binomial que calcula la cantidad de nucleocápsidas que se desarrollarán durante esa iteración dentro de la misma, este valor depende de la salud de la misma. Si se tiene un valor alto de nucleocápcidas se generan los fagos indicando que no es una buena solución y se saca del cuadro clínico para encontrar posibles mejores soluciones. De manera opuesta, si tiene un valor bajo de nucleocápcidas, hay mayores probabilidades de ser una buena solución y se mantendrá más tiempo en el cuadro clínico debido a que su producción de nucleocápsidas será baja. Es importarte notar que el objetivo es mantener en el cuadro clínico las bacterias que representen las mejores soluciones encontradas; éstas son las que son más resistentes a reproducir el virus.

El valor de LNR de cada genoma en el cuadro clínico se calcula comparando el valor de la mejor solución encontrada con la que se desea evaluar, es decir que el valor de LNR de una bacteria infectada puede verse modificado por el valor de la mejor solución encontrada en esa iteración. Este valor se calcula con la fórmula:

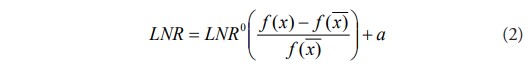
Donde, x – es la codificación del genoma de la bacteria que produce mejor solución según el estado del organismo, x el genoma evaluado, LNR0 es el valor inicial de NR y a es un valor fijo que permite que todas las bacterias produzcan nucleocápsidas cuando se realice el cálculo de la distribución binomial, de esta forma, aunque sean buenas soluciones, en determinado momento podrán generar la cantidad suficiente de nucleocápsidas para que el virus rompa el borde y salga a buscar mejores soluciones en su vecindario. De no permitir que las mejores soluciones desarrollen nucleocápsidas y se mantengan siempre en el cuadro clínico el algoritmo puede tardar más en encontrar la solución óptima debido a que no se exploraría el vecindario directo de estas soluciones.

La probabilidad de generar nucleocápsidas(NR) depende de la probabilidad Pr (probabilidad de que el suceso ocurra) y el valor LNR calculado con la fórmula 2, se utiliza una distribución binomial Bin(LNR,Pr ); mientras más pequeño es el valor del LNR menor será la generación de nucleocápsidas indicando que se está alcanzando solución óptima.

Cuando el organismo se ve atacado con los virus se produce una generación de anticuerpos para evitar el contagio de las bacterias. La capacidad de generar anticuerpos del organismo se representa mediante una distribución de probabilidad binomial Pan que elimina del vecindario elegido una cantidad de bacterias, a las restantes se evalúa el fitness con la anterior bacteria infectada, la mejor solución es elegida e incluida en el cuadro clínico sustituyendo a la anterior. Cuando no se ha encontrado en el vecindario una solución mejor, la bacteria infectada inicia un ciclo de reproducción lisogénico, lo que provocará un salto a otro vecindario.

2.2.3.3 Proceso de reproducción lisogénico

El ciclo de reproducción lisogénica se desarrolla dentro de la bacteria infectada en dos pasos. El primer paso es la infección, para representar este evento el VS coloca la bacteria dentro en el cuadro clínico. En la segunda parte del proceso el virus se mantiene oculto hasta que ocurre alguna acción externa que lo active provocando un cambio en la composición del ADN de la bacteria infectada, es decir, una mutación del genoma. Este fenómeno de activación se representa cuando se llega a un límite de iteraciones IT determinado.

Al igual que el proceso lítico, el valor de LIT de una bacteria infectada dependerá de la salud de la misma. Para un valor alto de fitness el valor de LIT será mayor, esto provoca una salida de dicha solución del cuadro clínico mas rápida y la entrada de otra que será la mutación de la misma. De esta forma el algoritmo de optimización salta de un espacio de búsquedas a otro evitando quedarse estancado en un punto.

Por el contrario, cuando el valor del fitness es bajo, es decir, la salud de la bacteria es bueno, el valor del LIT es bajo, esto provoca que se mantenga en el cuadro clínico por más tiempo. El valor de LIT se calcula en cada iteración del algoritmo con la fórmula (3), donde LIT0 es el valor inicial para LIT,

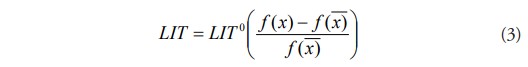
2.2.4 Finalización del proceso de infección

El proceso de infección de un organismo puede terminar de dos formas, el organismo lucha contra el virus y evita la multiplicación del virus o el virus logra infectar al organismo provocando la muerte del mismo. En este último caso el virus logró su objetivo. 

El VS representa el aislamiento virus en el organismo cuando la diferencia del valor del fitness de la mejor solución encontrada y un valor establecido es igual o menor que un margen deseado. En casos que se desee entrenar y verificar la eficiencia del algoritmo, y se conoce el valor la mejor solución, el margen puede fijarse a cero. Este margen se puede calcular con la fórmula 4.

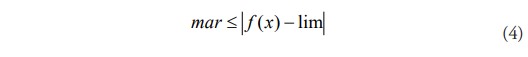
En el caso en que el algoritmo llegue a una cantidad de iteraciones determinadas y el VS haya sido incapaz de llegar al margen, el organismo no pudo de evitar la reproducción de nucleocápsidas en todas sus bacterias y sido infectado completamente. Esto significa que no se ha logrado llegar a una solución óptima del problema.

2.3 Algoritmo del sistema de virus

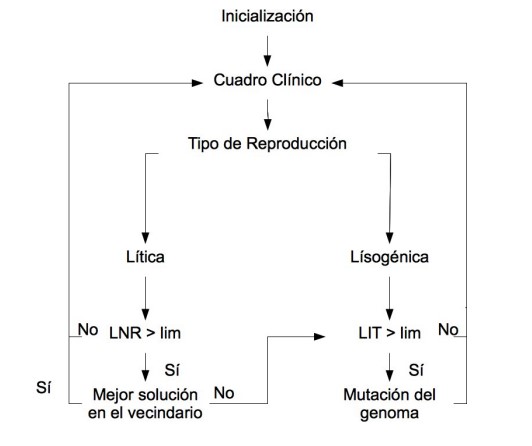
El algoritmo del VS consta de tres partes principales: inicialización, estado estacionario y finalización.

2.3.1 Inicialización

En este primer paso provee del estado inicial de las partes que conforman el sistema, tanto para el organismo como para el conjunto de virus.

1. Se genera el primer cuadro clínico donde se encuentran las primeras bacterias infectadas.
2. Se le asignan a cada bacteria un tipo de reproducción, lítica o lisogénica.
3. Se calcula el primer el valor de LNR para la reproducción lítica y de LIT para la reproducción lisogénica de cada bacteria en el cuadro clínico.
4. Se determina la forma en que el virus atacará al organismo, de forma masiva o selectiva. En este caso, como se mencionó anteriormente, se utilizará la infección selectiva.

2.3.2 Estado estacionario

El estado estacionario define la interacción virus organismo, durante cada iteración se evaluará el estado de cada una de las bacterias del cuadro clínico dependiendo de su tipo de reproducción.

1. Reproducción lítica: cada bacteria infectada comienza a reproducir nucleocápsidas en su interior, producto de la suma al LNR inicial del valor de la distribución binomial con probabilidad Pr, de haber llegado al límite establecido, dicha bacteria se convierte en un virus.

a. Sale del cuadro clínico y busca sus vecinos más cercanos que no producen anticuerpos y escoge la más débil. De no encontrar una mejor solución inicia un proceso lisogénico.

2. Reproducción lisogénica: se incrementa en uno el valor calculado de LIT simulando la acción externa que lo activa, y se compara si con este nuevo valor, de no llegar al límite IT establecido, la bacteria se queda en el cuadro clínico, en el caso contrario,

a. El genoma de esta bacteria infectada sale del cuadro clínico y es mutado, convirtiéndose en otra solución, esta solución sustituye la anterior del cuadro clínico.

Para ambos casos de reproducción, se realiza un control de repetición en el cuadro clínico antes de incluir una nueva solución, esto para evitar posible redundancia en los datos que están siendo evaluados. Luego que se actualiza el cuadro clínico durante la evaluación de cada bacteria infectada, asignándole un nuevo tipo de reproducción a cada bacteria, esto ayuda a la dinamización de la información y los procesos de búsqueda de nuevas soluciones.

Por último, se actualiza el estado del organismo, es decir, se busca la mejor solución encontrada con el objetivo de hacer los nuevos cálculos LNR y LIT de cada bacteria, estos cálculos se hacen para todas las bacterias independiente del tipo de reproducción asignada en el momento, debido a que un proceso lítico se puede convertir en un lisogénico y durante ese proceso necesitará información tanto de LNR como de LIT de la bacteria infectada.

2.3.3 Finalización

El proceso de estado estacionario se realizará hasta que se llegue a los límites establecidos en la sección 2.2.4, de número de iteraciones o de un valor límite de solución.

2.3.4 Diagrama de flujo

3. Resultados experimentales

En este capítulo se muestran los resultados de las pruebas realizadas para comprobar la eficiencia del algoritmo por infección por virus (VS). Primero, se realizan pruebas con funciones Onemax de diferentes longitudes de bits; estas funciones son de rápida implementación y permiten evaluar de forma efectiva el funcionamiento básico de un algoritmo de optimización. Los resultados fueron comparados con los obtenidos con un algoritmo genético (GA) que funciona simulando el crecimiento de los corales marinos.

Para elevar el nivel de complejidad de las pruebas se utilizaron funciones Engañosas, conocidas en inglés como Deceptive functions, con diferentes longitudes de bits. Estas funciones nos ayudan a comprobar la potencia de convergencia del algoritmo bajo condiciones más complicadas.

3.1 Experimentos con funciones Onemax

La función Onemax toma un individuo x (cadena n de bits de una longitud determinada), y devuelve un número igual a la suma de los valores de todos sus bits. El objetivo es encontrar el individuo que maximiza esta función, este valor es el que todos sus bits valen uno, coincidiendo en ese caso el valor de Onemax con la longitud del individuo (Doerr y Neumann, 2020). La fórmula general es:

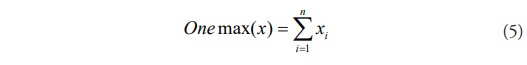
donde xi puede valer 0 o 1.

3.1.1 Parámetros configurados en el VS

Como se explicó en la sección 2.2, el VS posee una serie de parámetros y elementos que definen su comportamiento, estos parámetros vienen determinados por el tipo de problemas de optimización que se desee resolver, en este caso estamos trabajando con funciones Onemax de diferentes longitudes. En esta parte se define cómo se realiza la codificación de cada uno de estos elementos a fin de adaptarlos a este problema en particular. A continuación, se presentan los elementos configurados en el VS:

Genoma: cada bacteria infectada que es una posible solución, y está representada por un genoma que es una cadena de bits con una longitud determinada.

Estado del organismo: el primer cuadro clínico se elige de manera aleatoria dentro del espacio de posibles soluciones cumpliendo con las restricciones establecidas, en este caso cada genoma en el cuadro clínico debe cumplir con la cantidad de bits establecido. El cuadro clínico y la mejor solución en él representan el organismo.

Estado del virus: como se explicó en la sección 2.2.1 el estado del virus está compuesto por tres tuplas, genoma de la bacteria infectada, la cantidad de nucleocápside para la reproducción lítica calculado con la fórmula 2 y el número de iteraciones para la reproducción lisogénica calculado con la fórmula 3 < Genoma, NR, IT>.

Entrada del virus: está representado por el vecindario de cada una de las bacterias infectadas. Se debe elegir adecuadamente el vecindario en la reproducción lítica para poder encontrar los individuos más propensos a contagiarse e incluirlos en el cuadro clínico. Para esta prueba los vecinos se generan usando la distancia de bits, complementado una cantidad aleatoria de bits del genoma.

Proceso del organismo: consiste en la respuesta antigénica del organismo determinada por la probabilidad Pan que se aplica al vecindario elegido de la bacteria infectada, descrito en la sección 2.2.3.2.

Proceso del virus: está definida por el tipo de reproducción que se llevará a cabo en cada genoma del cuadro clínico, lítica o lisogénica. Esta asignación se hace manera aleatoria siguiendo las especificaciones de probabilidad presentadas en la sección 2.2.3.2. El proceso del virus también depende de los parámetros iniciales LNR0 y LIT0 al igual que de la probabilidad de reproducir nucleocápsides en el proceso lítico.

3.1.2 Resultados

Luego de configurar los parámetros iniciales necesarios para la configuración del VS. Se realizaron las pruebas con cadenas de bits de diferentes longitudes para la función Onemax, de esta forma se puede comprobar la potencia de convergencia del algoritmo mientras la complejidad del problema aumenta. Los valores de los parámetros de configuración básicos se presentan en la tabla 1, el genoma, determinado por la longitud de bits, el valor del cuadro clínico inicial, la probabilidad de reproducción lítica (PLIT), número inicial de nucleocapsidas en la reproducción lítica (LNR), número de iteraciones iniciales para la reproducción lisogénica (LIT), probabilidad de generar nucleocapsidas (Pr) y probabilidad de la bacteria de desarrollar anticuerpos (Pan). Los valores para cada prueba son muy parecidos debido a que la función objetivo y las características generales del problema son las mismas. Los valores que más influencian en la configuración son el tamaño del cuadro clínico y los valores de LIT debido a que el espacio de búsqueda de posibles soluciones aumenta.

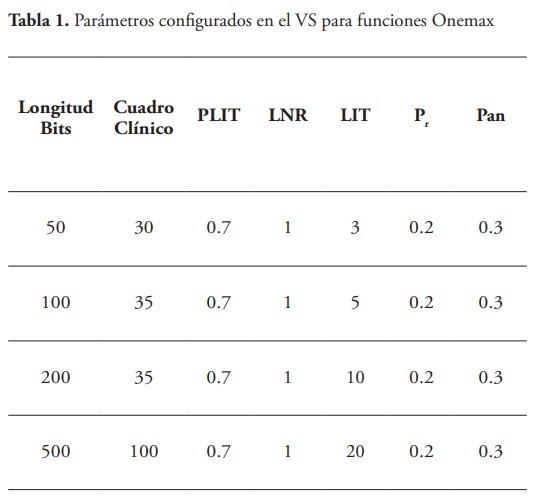
La finalización del algoritmo se determinó con un número máximo de 5000 iteraciones o un margen de 0 (que significa que se espera encontrar el mínimo global). Cada configuración se ejecutó 10 veces para comprobar la coherencia de los resultados. El resultado de la media de cada prueba se muestra en la figura 5 en conjunto con los resultados obtenidos del sistema de corales marinos.

A partir de estos resultados, podemos tener varias conclusiones relativas al funcionamiento del VS y su aparente ventaja sobre el GA de corales marinos. En primer lugar, el VS converge más rápido en todas las pruebas dentro de los parámetros establecidos (número de iteraciones) encontrando el resultado óptimo, mientras que el GA requiere un número mayor de iteraciones para lograr el resultado deseado. En segundo lugar, se puede observar la influencia significativa del incremento de la longitud de bits a optimizar, esto supone un mayor esfuerzo al algoritmo y mayor número de iteraciones.

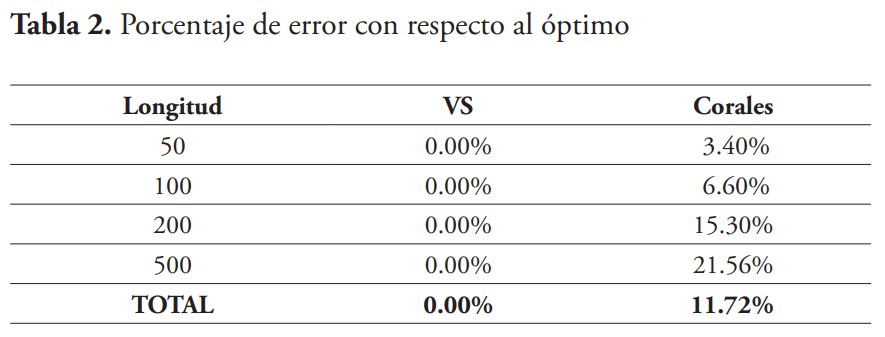
La tabla 2 muestra un resumen del porcentaje de error obtenido en cada prueba. Tal y como se pudo apreciar anteriormente en los resultados de la figura 5, el VS tiene un porcentaje de error de 0 % debido a que en cada caso pudo encontrar el óptimo deseado. Mientras que el GA de corales marinos tiene un índice de error que va creciendo según la complejidad del problema aumenta.

Para calcular el porcentaje de error para el GA se utilizó el valor obtenido en el número de iteración donde el VS encontró el óptimo. De esta forma se compara la diferencia entre ambos algoritmos en el mismo punto de referencia.

3.2 Experimentos con función Engañosa (Deceptive Function)

Las funciones Engañosas (Deceptive Function) fueron creadas con el objetivo de diseñar pruebas más complicadas para los GA y determinar su potencia de convergencia ante problemas que no fueran del tipo combinacionales, donde la mejor solución se construye con la hipótesis de construcción por bloques (BBH), la cual establece que la mejor solución en un algoritmo se encuentra ensamblando soluciones parciales. Debido a que las soluciones de funciones Engañosas no se construyen en bloques la eficiencia de los GA es muy baja ante este tipo de problemas de optimización.

La complejidad de una función engañosa radica en que tiene por lo menos dos tipos de soluciones óptimas, una global para todo el espacio de búsquedas, y una local para un determinado vecindario de soluciones. El problema principal es que los algoritmos tienden a encontrar la solución local, que es una solución sub-óptima y es llamada la solución engañosa. Estas soluciones están creadas por bloques, donde cada uno tiene un valor determinado, el fitness se calcula sumando dichos valores. El valor de estos bloques se asigna de forma tal que los bloques que representan la solución engañosa tengan un valor alto, mayor que cualquier otro y con muy poca diferencia del bloque que formará la solución global (Du y Swamy, 2016).

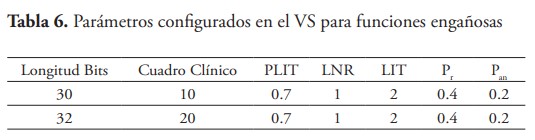
Este tipo de pruebas permitirán comprobar el funcionamiento del VS bajo condiciones más complicadas que las tenidas con las funciones Onemax. Para las pruebas se utilizaron dos tipos de funciones totalmente engañosas, una con bloques de 3 bits y un genoma de 30 bits (10 bloques), y una segunda de 4 bits con genoma de 32 bits (8 bloques). 

3.2.1. Valores de las funciones deceptivas

El objetivo del algoritmo es encontrar el máximo global compuesto por bloques todos a 1, el algoritmo debe tener la capacidad de salir de la solución engañosa, esta solución está compuesta por bloques todos a 0. La tabla 3 establece las condiciones que debe cumplir la función compuesta por bloques de 3 bits para ser completamente engañosa.

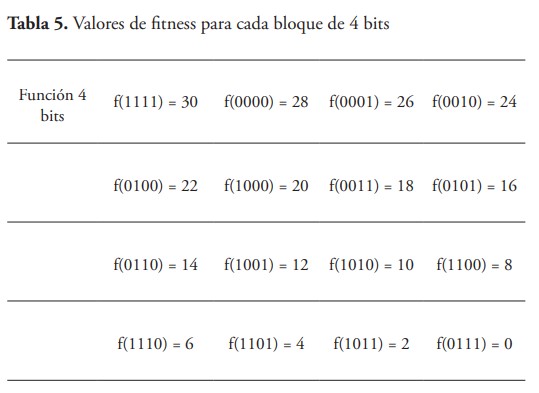
La tabla 4 presenta los valores de fitness para cada bloque de 3 bits que cumplen con las condiciones antes mencionadas. El valor de fitness total de cada genoma se representa por la suma de las aportaciones de cada bloque. La tabla 5, por otro lado, presenta los valores totalmente engañosos correspondientes a una función de 4 bits.

El valor óptimo del fitness para la configuración de 3 bits y genoma de 30 bits es de 300 y el valor engañoso 280, mientras que para la función de 4 bits y genoma de 32 bits el valor óptimo de fitness es de 240 y el valor engañoso de 224. Los valores óptimos y engañosos para ambas funciones están muy cercanos, esta es la razón por la cual las funciones engañosas representan un desafío para el algoritmo.

3.2.2 Resultados

Para configurar el VS con estas funciones solo fue necesario cambiar la función que calcula el fitness, sustituyéndola por una que calcula el valor total del fitness del genoma compuesto por los valores de cada bloque. El resto del algoritmo sigue siendo el mismo.

La configuración de los parámetros necesarios en el VS para realizar estas pruebas son los mismos que la presentadas en la parte 3.1.1. La tabla 6 muestra los valores, los cuales son muy parecidos, con una ligera variación en el tamaño del cuadro clínico debido al tamaño del espacio de soluciones.

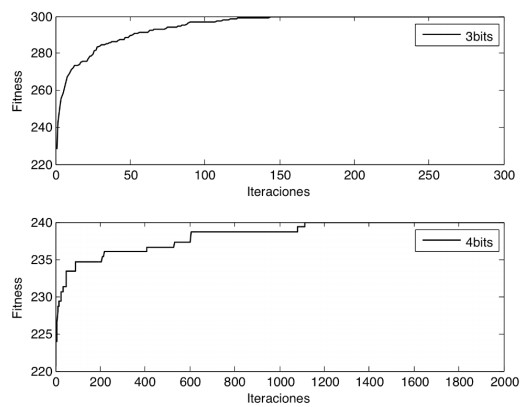
El número de iteraciones fue fijada a 4000 y el margen a 0 que representa el resultado de encontrar el valor óptimo según la fórmula 4. Para comprobar el comportamiento del algoritmo con estas dos configuraciones se ejecutó 5 veces en cada caso para luego obtener la media de los valores. Los resultados se muestran en la figura 6 donde podemos observar que, a pesar de las características engañosas que tiene dichas funciones, el VS tuvo la capacidad de encontrar el máximo global en ambos casos. Es de notar, que para la función de 4 bits el algoritmo se detuvo por una cantidad de iteraciones en la solución engañosa hasta que logra salir de ella y encuentra la solución óptima.

4. Conclusiones

En este artículo se presenta el desarrollo y la implementación de un método heurístico a partir del proceso natural de un virus infectando las células de un organismo. La aplicación de la analogía estuvo basada en la propuesta de Cortés et al. (2008), en el cual el objetivo del algoritmo es el triunfo del organismo, lo que significa que debe aislar el virus luego de ser infectado encontrando la bacterias más resistentes a la multiplicación, entre las que se encuentra la mejor solución del problema de optimización.

Para probar el funcionamiento y la correcta implementación del algoritmo, se utilizaron dos tipos de funciones; Onemax (con diferentes longitudes) y funciones Engañosas, llamadas también Deceptive Function (con diferentes longitudes de bloques). Utilizando la herramienta computacional Matlab se lograron resultados muy favorables. De las 4 pruebas realizadas con la función Onemax (longitud de 50, 100, 200 y 500 bits) el VS logró encontrar la solución óptima en todos los casos. De la misma forma con las funciones Engañosas donde las características de dichas funciones no lograron evitar que el VS encontrara la mejor solución en ambos casos (bloques de 3 y 4 bits).

A manera de comparación con otros algoritmos de optimización, se realizaron las mismas pruebas de las funciones Onemax en un algoritmo genético (GA) inspirado en el proceso natural de crecimiento de corales marinos. Esta comparación mostró la gran ventaja del VS frente al GA, donde de las 4 pruebas realizadas, el GA solo pudo encontrar 1 solución óptima con las condiciones impuestas para ambos algoritmos, en las demás condiciones el GA no pudo encontrar una solución óptima. Dado los resultados favorables obtenidos se puede concluir que este algoritmo se puede utilizar para resolver problemas de optimización de mediana y alta complejidad. Un ejemplo de aplicación de problemas de alta complejidad en redes de comunicaciones es el presentado por Cortés et al. (2008) en donde el VS resuelve el problema de Steiner.