Respuesta sísmica local de la presa Las Dos Bocas utilizando un análisis no lineal

La isla Hispaniola, que República Dominicana comparte con Haití, se encuentra asentada en el borde Norte de la placa tectónica del Caribe, y como en la mayoría de bordes de placas tectónicas, en los límites de la placa del Caribe, hay una actividad sísmica importante, lo que la convierte en una zona de “alta peligrosidad sísmica”, tanto en el interior de la isla como en su zona marítima. 

Durante la ocurrencia de un sismo, se libera la energía de deformación acumulada en las zonas de contacto entre placas tectónicas de forma brusca y relativamente rápida. esta energía liberada se transforma en ondas sísmicas que se propagan, se reflejan, refractan y atenúan por el interior de la Tierra hasta llegar al sustrato rocoso que está situado bajo el terreno de cimentación de la estructura. Por encima de este, las capas de suelo actúan como filtros de frecuencias, de manera que modifican la energía que transmiten a la estructura. Los terrenos blandos amplifican las señales cuyas frecuencias predominantes son bajas (períodos altos). Otros aspectos como el aumento de las presiones intersticiales del terreno durante los terremotos pueden alterar incluso el estado físico de los suelos, ya que se producen fenómenos de licuefacción. Asimismo, pueden producirse otros efectos como roturas del terreno, deslizamientos y caídas de rocas. Dichos fenómenos, conocidos como efectos inducidos, provocan la pérdida de capacidad portante del terreno y son causa directa de daño estructural.

Los terremotos, en los últimos cincuenta años, han demostrado el papel de los efectos del suelo en la distribución y magnitud de los daños. Cuando se produce un terremoto, el suelo circundante y los elementos estructurales pueden mostrar un comportamiento no lineal. En la práctica común, solo se evalúa el comportamiento no lineal de los elementos estructurales, pero, en realidad, el suelo alcanza el límite de su comportamiento elástico antes que los elementos estructurales. En general, los efectos de interacción suelo-estructura se suponen beneficiosos, por lo tanto, se ignoran. Sin embargo, un conocimiento más preciso de la respuesta sísmica estructural esperada puede permitir reducir el coste de la estructura y mejorar la práctica de la ingeniería sísmica.

La importancia que presenta la respuesta del suelo sobre el que se ubica una estructura ante un posible movimiento sísmico, así como la interacción suelo-estructura en terrenos blandos, son cuestiones que adquieren especial relevancia en el diseño de obras. Ello exige un conocimiento previo de las características de amplificación del suelo. Dado que la no linealidad del comportamiento del suelo es bien conocida (Beresnev, 1996), el enfoque lineal debe ser modificado para proporcionar estimaciones razonables de respuesta del terreno para los problemas prácticos de interés y una mejora en la calidad de datos.

En la actualidad se dispone de un gran número de procedimientos numéricos para estimar la respuesta dinámica de un suelo. Estos procedimientos consideran en mayor o menor medida la complejidad del comportamiento dinámico de los suelos, en los cuales se evidencia un claro comportamiento no lineal (Aki & Ikura, 1991). De todas las metodologías disponibles, la que ha sido utilizada con mayor frecuencia es la propagación unidimensional de onda cortante, utilizando un modelo lineal equivalente. 

En regiones sísmicamente activas se reconoce la necesidad de realizar análisis adecuados y de investigar cómo se comportarían las grandes estructuras diseñadas antes de los códigos y prácticas vigentes, durante la ocurrencia de un sismo de magnitud importante. Entre tales estructuras se destacan las presas de embalse, ya que un daño sobre las mismas puede tener efectos en una gran zona de influencia, pueden variar desde pérdidas económicas (por necesidad de reparación de la estructura, inundaciones en cultivos, o verse afectado el sistema de generación de energía o de distribución de agua) hasta la pérdida de vidas humanas por inundaciones en poblados cercanos.

El presente artículo incluye, fundamentalmente, la evaluación de la respuesta sísmica para el punto específico Presa Las Dos Bocas, realizando un análisis no lineal del modelo unidimensional del suelo, teniendo en cuenta que el depósito de suelo es estratificado, con amortiguamiento y que el lecho rocoso es elástico.

2. Sismicidad y descripción de la zona de estudio

La República Dominicana cuenta con una alta sismicidad, debido a la posición de la isla Hispaniola, lo que provoca que sea considerada como de alto riesgo sísmico. La sismicidad de la República Dominicana se debe básicamente a los movimientos transformantes (falla Septentrional) y de subducción interplacas (falla Hispaniola Norte) entre las placas Norteamericana y del Caribe al norte de la Hispaniola y al noroeste del Canal de la Mona; a la fosa Los Muertos al sur de la isla; a la falla Enriquillo-Plantain Garden al oeste y suroeste de la Hispaniola; a las fallas de Ocoa, Guácara y Hatillo en la zona central del país; y a la probable interacción de varias microplacas dentro de una zona compleja de borde de placa.

Registros históricos e instrumentales dan cuenta de la sismicidad en la Isla Hispaniola. Más de quince terremotos con intensidades MM ≥ viii han ocurrido en o cerca de la isla en los pasados 500 años (Chalas Jiménez, 1989). Todos esos terremotos causaron grandes daños en la República Dominicana. Dignos de mención son los terremotos de 1562, 1673, 1751, 1842 y 1946, por lo que, es de esperarse que en un futuro relativamente cercano el país sea afectado por una fuerte sacudida sísmica, ya que desde 1946 hasta el presente han transcurrido 73 años.

Sin embargo, a pesar del alto riesgo sísmico de nuestro territorio y de la alta probabilidad de ocurrencia de un evento importante en los próximos años, el país no está preparado ni física, ni síquica, ni logísticamente para enfrentar un terremoto de magnitud superior a 7.0 grados en la escala de Richter, puesto que la mayor parte de la población dominicana, por no haber vivido la experiencia del último gran terremoto, tiende a subestimar el riesgo sísmico en el país (León & Ciencias, 2002). Esta subestimación del riesgo sísmico permite que se levanten edificaciones en áreas poco aptas y aunque los códigos de construcción antisísmica ya existen en la República Dominicana, los escasos conocimientos o actualización de los avances en la ingeniería sísmica pueden obstaculizar los planes de construcción adecuados en zonas sísmicamente vulnerables.

Para esta ocasión este estudio se centrará en el análisis probabilístico de amenaza sísmica de la Presa Las Dos Bocas. El proyecto “Las Dos Bocas” se encuentra aguas arriba de la confluencia de los ríos El Cole y Dos Bocas afluentes del río Vallejuelo, ubicado al suroeste de San Juan de la Maguana, al sureste de El Cercado y al oeste de Vallejuelo, en el lado norte de la sierra de Neyba, la cual está formada por estratos de rocas calizas plegadas que originan una serie de anticlinales y sinclinales que generan las montañas y los valles de la zona.

3. Comportamiento no lineal

El estudio de leyes constitutivas o modelos del comportamiento dinámico de suelos es necesario debido, fundamentalmente, a que los suelos sometidos a ensayos cíclicos de laboratorio exhiben un comportamiento no lineal e histerético (Hardin & Drnevich, 1972).

Entre los modelos de comportamiento dinámico más empleados se encuentran:

• Correlaciones empíricas de Seed e Idriss (1970)
• Modelo hiperbólico de Hardin y Drnevich (1972)
• Modelo de Ramberg-Osgood (1973)

Estos modelos aceptan como válida la regla de Masing para idealizar la curva esfuerzo deformación del suelo bajo carga dinámica (ver (Figura 2).

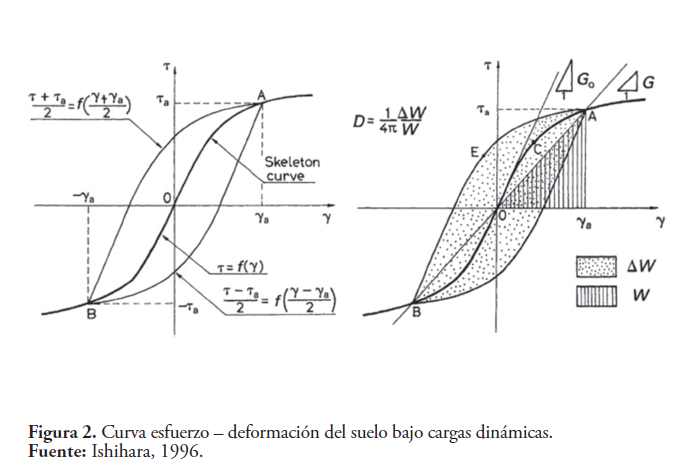
La regla de Masing establece que la curva esfuerzo-deformación inicial (o virgen) del suelo se expresa como:

$T = f \left(y\right)$ (1)

Mientras que las ramas de descarga y de recarga se definen con 

$\frac{t-t_a}{2}= f \left(\begin{array}{c}y-y_a\\ 2\end{array}\right)$(2)

donde τ_a es la amplitud del esfuerzo cortante y γ_a la deformación angular. El comportamiento no lineal del suelo es tomado en cuenta por la dependencia de los parámetros de rigidez (G) y el coeficiente de amortiguamiento del suelo (ζ) en función de la deformación alcanzada por el sismo. El módulo de corte generalmente se define como la pendiente de la línea secante que conecta el punto final del bucle del ciclo de histéresis para una deformación de corte, como se muestra en la Figura 2. En términos generales, se pueden obtener dos parámetros importantes “lineales equivalentes” directamente de la curva. El primero es el módulo de corte secante:

$G=\frac{t_a}{y_a}$(3)

que nos da la información de la inclinación de la curva. El segundo parámetro es el coeficiente de amortiguamiento histerético:

 

ζ = $\frac{W_D}{4\mathrm{\pi } {\mathrm{W}}_{\mathrm{E}}} = \frac{∆ E}{2\mathrm{\pi } {\mathrm{GY}}^2}$(4)

donde ∆E es la energía disipada por el suelo en un ciclo y por unidad de volumen (∆E = área punteada en la curva de la Figura 2), W_D es la energía disipada y W_E es la energía máxima de deformación. Los parámetros G y ζ bastan para describir el comportamiento del suelo para cierto tipo de análisis de respuesta del terreno.

4. Modelo lineal equivalente

Los modelos más simples y más comúnmente utilizados para el estudio del comportamiento dinámico de los suelos que trabajan con la teoría de la elasticidad son los modelos de suelo lineal equivalentes, que consideran a un suelo como un material viscoelástico lineal. En ellos el comportamiento no lineal es tenido en cuenta mediante la dependencia de los parámetros de rigidez (G) y amortiguamiento del suelo (ζ) con la deformación. Sin embargo, no permiten que se desarrollen deformaciones permanentes. La rigidez del suelo es caracterizada normalmente por el módulo de corte máximo (Gmax), el cual se encuentra para pequeñas deformaciones, y por una curva de reducción del módulo (G/Gmax) en la que se observa como el módulo de corte decrece para grandes deformaciones. El comportamiento amortiguador del suelo queda caracterizado por el coeficiente de amortiguamiento (ζ) que crece al crecer la amplitud de la deformación.

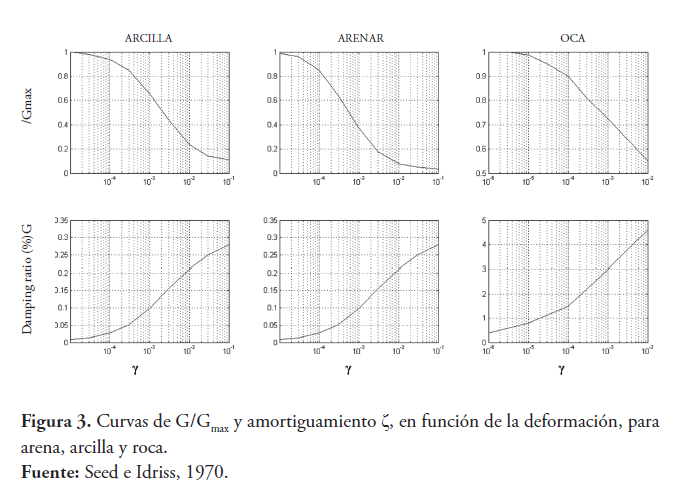
El módulo de corte dinámico y la relación de amortiguamiento en función de la deformación alcanzada por el sismo fueron primero introducidos por Seed e Idriss (1970) y esencialmente a análisis lineales equivalentes. Tales curvas fueron desarrolladas para diferentes materiales del suelo; por ejemplo, curvas para arena y arcilla fueron propuestas por Seed e Idriss (1970), y para grava, por Seed, Wong, Idriss, y Tokimatsu (1986). Estos autores proponen las curvas de degradación G/Gmax y la relación de amortiguamiento de acuerdo con los niveles de deformación para diferentes tipos de suelo. Por ejemplo, en las siguientes validaciones de este trabajo consideramos las curvas relacionando el módulo de corte y la relación de amortiguamiento que se muestran en la Figura 3 para arena, arcilla y roca, respectivamente. 

5. Movimiento en el afloramiento rocoso

Generalmente, el movimiento de control utilizado para el análisis de suelo se define en superficie mediante un espectro de respuesta o una historia temporal correspondiente a la base rocosa por lo que se conoce como “Afloramiento rocoso”. A partir de él se precisa predecir el movimiento en el sustrato rocoso cubierto por el depósito de suelos. Este problema se ha resuelto para el caso especial de un sistema de capas que cubre a un semiespacio elástico, uniforme y lineal. En Germoso (2015) se justifica que en la base de la columna de suelo el medio espacio del lecho de roca puede ser reemplazado por un esfuerzo cuyo comportamiento está modelado por:

${T_0}^{*} = p{C}_s U_s p{C}_s{U_0}^{*}$(5)

donde ρ es la densidad de la roca madre, C_s la velocidad de la onda de corte, ${U_s}^{*}$ la velocidad del afloramiento de roca, ${U_0}^{*}$ la velocidad en la base de la columna del suelo, que coincide con la interfaz del medio suelo-roca madre y ${T_0}^{*}$ es el esfuerzo cortante en esa posición. En Germoso (2016) esta condición límite se aplicó en la base del depósito del suelo que se analizó en el régimen no lineal, teniendo en cuenta los efectos del medio espacio subyacente de la roca madre.

6. Análisis de respuesta de sitio Presa Las Dos Bocas

Para el análisis de la respuesta de sitio, se deben considerar varios factores, la descripción del perfil geológico, que nos dará información de los valores iniciales de las propiedades dinámicas y de la estratigrafía del depósito de suelo, la clasificación sísmica del sitio, en el que se tomará en consideración la alta sismicidad y si la zona de estudio pertenece a un campo lejano o cercano y las aceleraciones máximas esperada en roca. Una vez establecidos estos parámetros se procede a la determinación del comportamiento no lineal del suelo, en el que se considerará el modelo lineal equivalente descrito anteriormente; en este método el comportamiento no lineal se ajustará en un proceso iterativo para obtener un nivel efectivo de deformación de corte inducido por el suelo. En el proceso de análisis se toman valores estimados de módulo de corte y amortiguamiento para un sismo de entrada y se calcula la deformación efectiva de corte para un tipo de suelo con sus diferentes estratos.

6.1. Descripción del perfil geológico

Para determinar la geología específica del sitio de presa, Betances y Ciriaco (2015) realizaron un programa de investigación del subsuelo mediante la ejecución de una campaña de sondeos mecánicos con extracción de núcleos de roca y realización de ensayos Lugeon, indicando las siguientes características:

1. Se perforaron siete sondeos, y fueron numerados desde el No. 6 hasta el No. 12.
2. Los siete sondeos fueron distribuidos en toda la longitud de la fundación de la presa, desde la margen izquierda hasta la margen derecha y en el lecho del río.
3. Los sondeos No. 6, 7, 8, 10 fueron verticales, mientras los sondeos No. 9,11 y 12 fueron inclinados 35º hacia la margen derecha, contra el buzamiento de los estratos.
4. En los sondeos verticales se ejecutaron ensayos de penetración (SPT).
5. En la margen izquierda, el sondeo No. 10 atraviesa en toda su longitud estratos de lutita de color crema, los cuales muestran una secuencia de estratos medianamente estructurados y consolidados, de manera ocasional intercalada con estratos más rígidos y fracturados de limolita.
6. Los sondeos 6 y 11 atraviesan una terraza aluvial con un espesor promedio de 14 m de profundidad y continúan dentro de una secuencia estratigráfica de lutita y limolita y dada su buena calidad, la roca base con mejores condiciones geotécnicas para la fundación de la presa. La cota media del techo de esta terraza es 875.50 msnm, aproximadamente, siendo la profundidad media de los sondeos de 37.5 m. La roca base se encuentra en la cota 862 msnm, aproximadamente.
7. El sondeo 12 atraviesa el aluvial en una terraza más baja, aproximadamente en la cota 864 msnm. Tiene una profundidad de 25 m y encuentra la roca base a 3.60 m de profundidad, en la cota 861 msnm.

6.2. Geofísica y Geotecnia

Para dar soporte a los estudios de respuesta dinámica del suelo del sitio a las excitaciones sísmicas, además de la descripción geológica, se pudo conocer la columna estratigráfica del sitio y las propiedades de los suelos a través de la campaña de sondeos mecánicos con extracción de núcleos de roca. Las velocidades de corte en cada uno de los estratos del suelo se determinaron con una campaña geofísica realizada por la empresa Geoconsult, mediante el método MASW (Multichannel Analysis of Surface Waves), hasta una profundidad de 30 m.

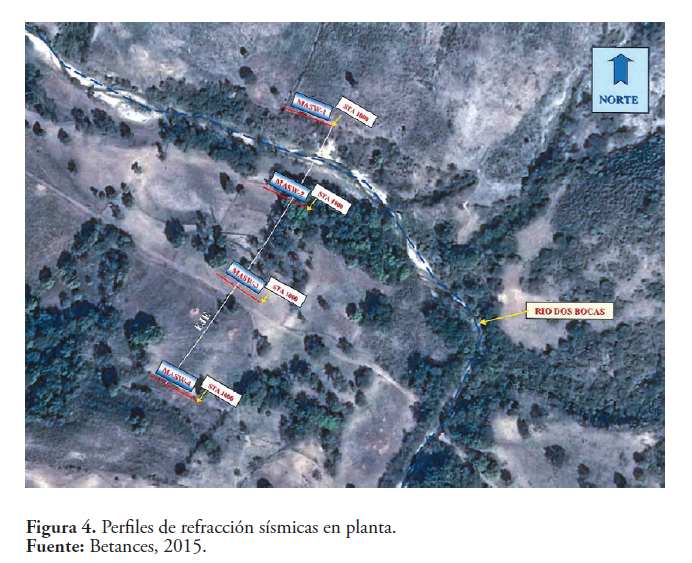
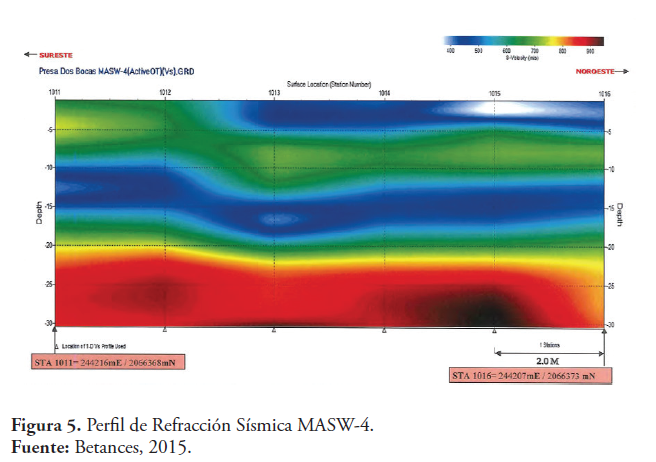
Las velocidades de la onda de corte Vs, han sido calculadas para diferentes estratos. Las Figuras 4 y 5, muestran el perfil de refracción sísmica MASW-4 y las velocidades de las ondas de corte Vs, respectivamente. El Estudio Geotécnico consistió en la realización de siete (7) sondeos en el eje de la Presa, con profundidades que van desde 25.00 m a 45.00 m.

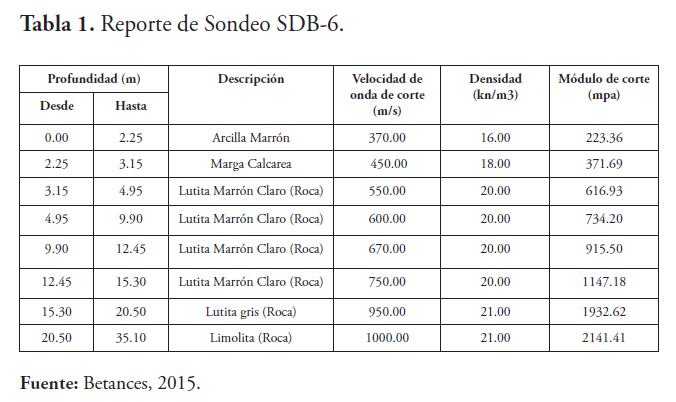
Para el presente estudio se eligió como perfil del suelo uno de los sondeos que se consideró como el más representativo del suelo subyacente, para fines de obtener la respuesta dinámica. Esta columna de suelo, con la descripción estratigráfica y geológica de los distintos estratos, le corresponde al sondeo SDB-6, mostrado en la tabla 1.

6.3. Fuentes Sísmicas

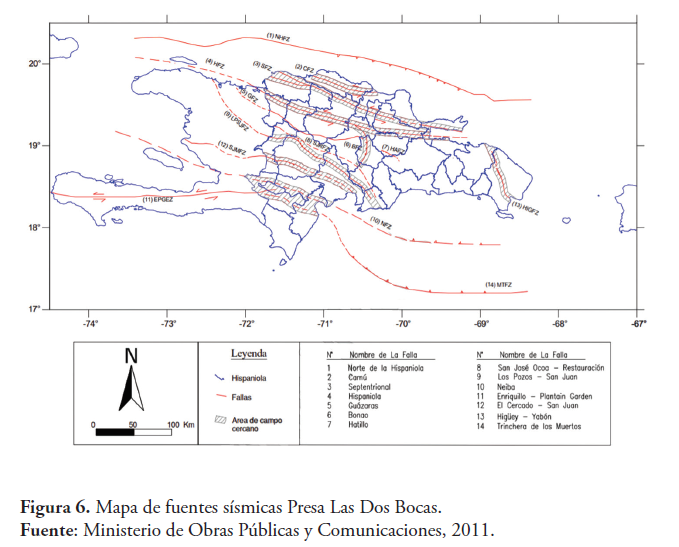
La amenaza sísmica de la Presa Las Dos Bocas comprende todas las fallas geológicas y áreas de fuentes activas dentro de un radio de 200 Km a partir de la localización del proyecto, incluyendo la Zona de Deformación Hispaniola Norte, la falla Septentrional, la Zona de Deformación Fosa Los Muertos, la falla Enriquillo-Plantain Garden, y las zonas de fallas Ocoa-Matieux-Neyba y Guácara-Hatillo-Bonao, como se muestra en la Figura 6.

6.4. Clasificación sísmica del sitio

6.4.1. Zona Sísmica

Según el Reglamento para el Análisis y Diseño Sísmico de Estructuras, el R-001, la República Dominicana se considera dividida en dos zonas, de acuerdo a sus niveles de aceleración sísmica espectral de referencia Ss, para un período de retorno de 2,475 años, con una probabilidad de excedencia de un 2 %, en 50 años. Y según la tabla 2 (artículo 10, p. 7) del reglamento, la Provincia San Juan pertenece a la Zona Sísmica ii.

1. Zona i: zona de alta sismicidad. Aceleración sísmica espectral de referencia mayor que 0.95 g.
2. Zona ii: zona de mediana sismicidad. Aceleración sísmica espectral de referencia menor o igual que 0.95 g.

6.4.2. Clasificación de sitio

El Proyecto Presa Las Dos Bocas se encuentra a más de 5 km de la falla más cercana (El Cercado-San Juan) por lo que se clasifica como campo lejano. El R-001, en su artículo 12, establece que los suelos serán clasificados según se indica en la Fig. 7 del reglamento (Figura 7) en función de las velocidades de ondas de corte Vs y/o el número de golpes del ensayo de penetración estándar “N”, o usando la resistencia al corte sin drenar, Su.

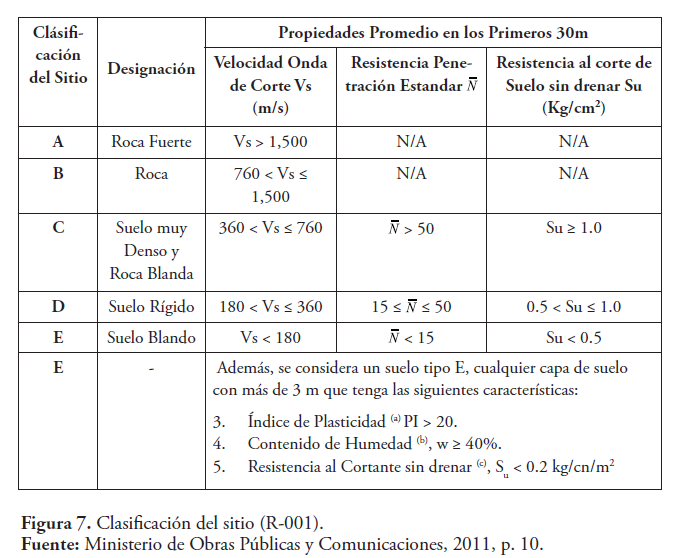
En el perfil MASW-4(2-D), Figura 5, de la velocidad de onda de corte (Vs) en los primeros 5.0 metros de profundidad los valores de velocidad varían entre 370 y 550 m/s (colores azules), debajo de este estrato y hasta los 10.0 – 12.5 metros de profundidad los valores de velocidad varían entre 750 y 950 m/s (colores amarillos, naranjas y rojos). Desde 12.5 hasta los 20.0 de profundidad aproximadamente los valores de velocidad varían entre 600 y 720 m/s (colores verdes). La velocidad promedio de la onda de corte en los primeros 30.0 metros de profundidad (Vs₍₃₀₎), muestra valores de V_s(30) comprendidos entre 598 y 645 m/s. Estas velocidades son mayores de 360 m/s y menores de 760 m/s. Según el R-001, Figura 7, para este rango de velocidades la clasificación sísmica del sitio es C.

6.5. Aceleración máxima del terreno

Se han realizado construcciones importantes en zonas cercanas al sitio de la Presa Las Dos Bocas, tales como la Presa Monte Grande y Presa Yacahueque. Y puesto que las aceleraciones contenidas en el R-001 son un tanto genéricas, para el diseño de estos proyectos se realizaron análisis probabilístico en términos de aceleraciones en la base rocosa, obteniendo así resultados que coinciden bastante con los obtenidos en estudios similares realizados en el país.

Tres aceleraciones máximas fueron obtenidas en el Estudio Probabilístico de Amenaza Sísmica en la Base rocosa, para el sitio Presa Yacahueque. Estos valores de aceleraciones máximas, determinados para diferentes niveles de riesgo, serán los que utilizaremos para el sitio de la Presa Las Dos Bocas, y son los siguientes:

1. Para una probabilidad de excedencia de un 10 % en 50 años, es decir, para un Periodo de Retorno de 475 años, PGA= 0.308 g.
2. Para una probabilidad de excedencia de un 5 % en 50 años, es decir, para un Periodo de Retorno de 975 años, PGA= 0.397 g.
3. Para una probabilidad de excedencia de un 2 % en 50 años, es decir, para un Periodo de Retorno de 2,475 años, PGA= 0.526 g.

Estas aceleraciones son utilizadas en este estudio para escalar una suite de registros acelerográficos de terremotos reales.

6.6. Selección de terremotos específicos del sitio

Para este estudio, dado la falta de registros sísmicos de aceleraciones fuertes en la zona, será necesario utilizar registros sísmicos que corresponden a fuentes sismo tectónicas con mecanismos focales iguales a los de las fuentes sísmicas asignadas al sitio de la Presa Las Dos Bocas, localizadas a distancias similares y registrados por estaciones acelerográficas situadas sobre terrenos con propiedades dinámicas similares a las del suelo en el lugar del proyecto. Los registros seleccionados corresponden a los presentados en la tabla 2.

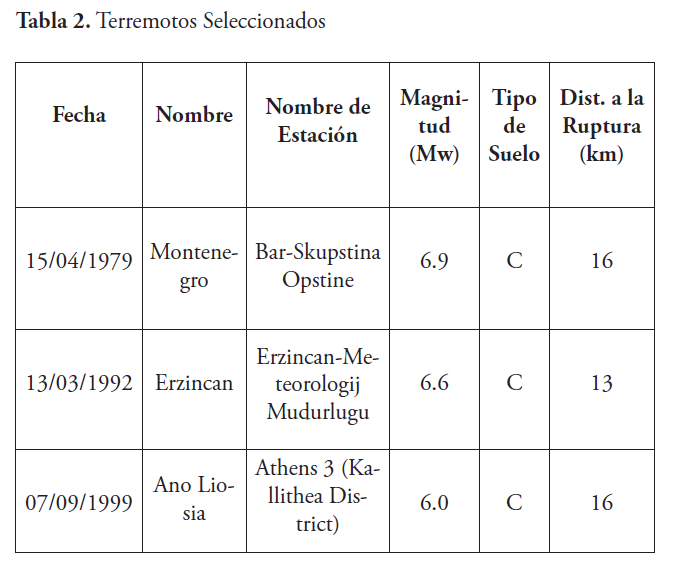
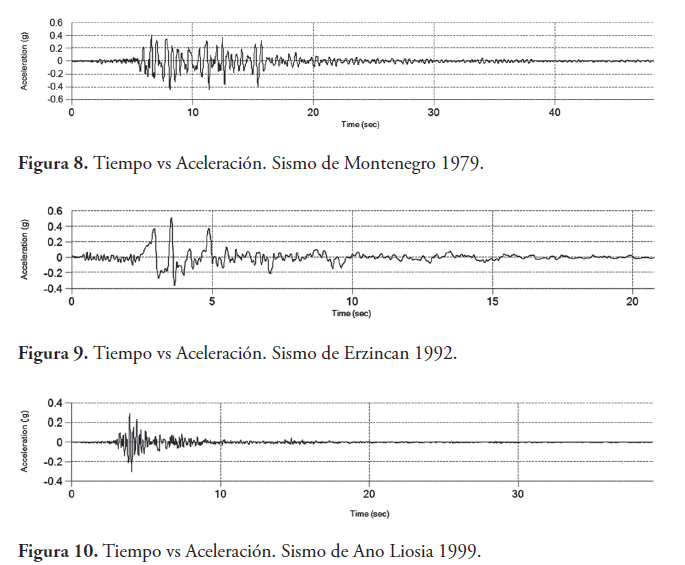
Los valores de aceleraciones máximas determinados para los períodos de retorno de 475, 975 y 2475 años, serán los que utilizaremos en el análisis de respuesta de sitio para escalar los registros acelerográficos de los sismos presentados en la tabla 2. En las Figuras 8, 9 y 10 se presentan los registros, sin escalar, de los terremotos seleccionados.

7. Resultados

A través del programa de cálculo EERA (Equivalent-linear Earthquake site Response Analyses, Bardet Ichii & Lin, 2000), que aplica la hipótesis del comportamiento no lineal mediante un análisis lineal equivalente del suelo empleando el procedimiento numérico para un modelo de suelo unidimensional, se muestran los resultados del análisis de respuesta sísmica de sitio. Para el análisis utilizaremos los registros acelerográficos de los sismos presentados en la tabla 2, escalados para los valores de aceleraciones máximas determinados para los períodos de retorno de 475, 975 y 2475 años.

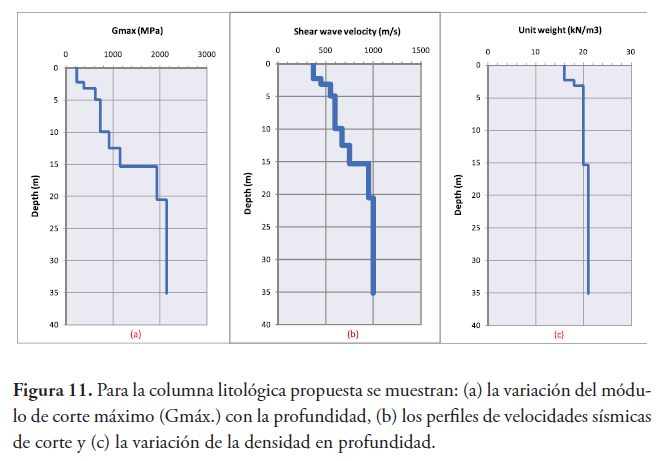
Los resultados presentados en esta sección son considerando la señal de entrada como un movimiento en el afloramiento (ver sección 5). En la Figura 11, EERA nos muestra la variación del módulo de corte, los perfiles velocidades sísmicas de corte, y la variación de la densidad en profundidad tomados como valores iniciales del modelo.

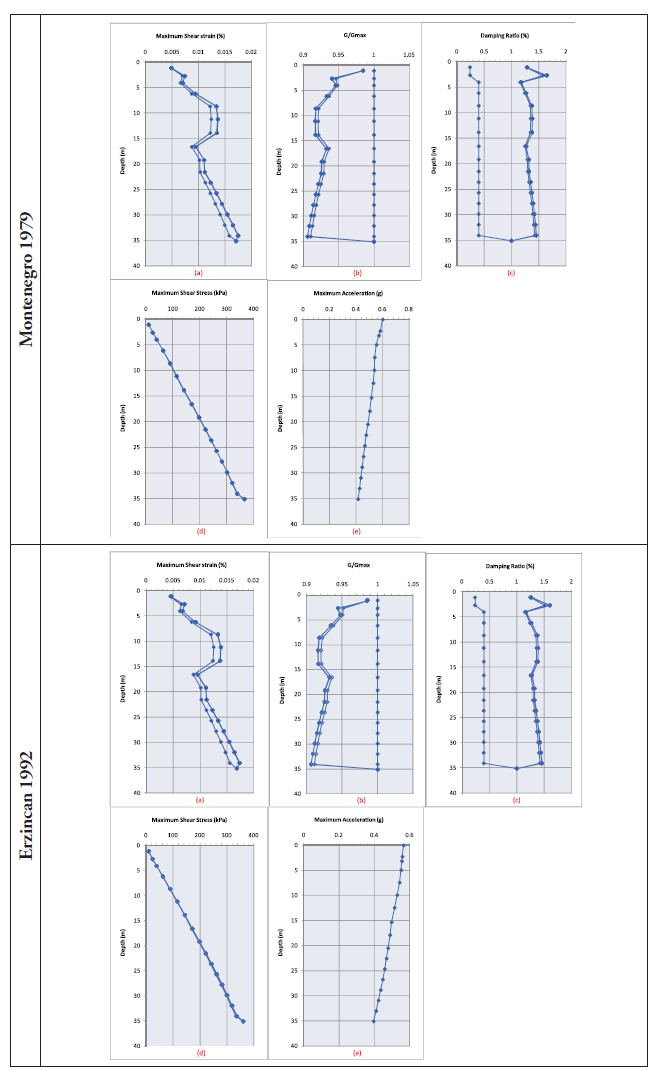
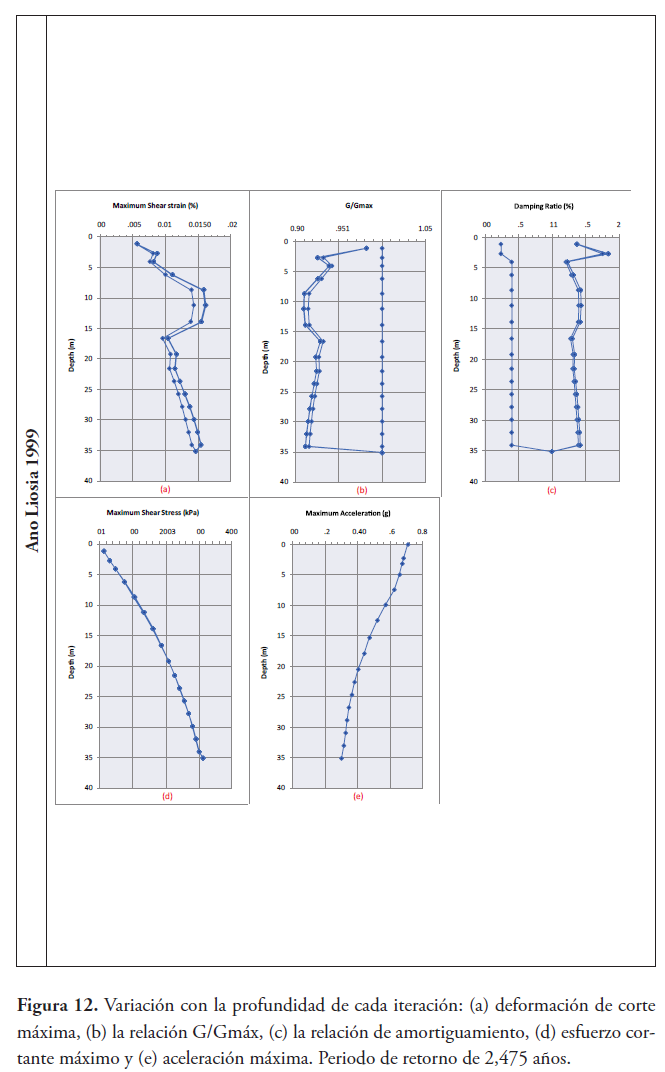
La Figura 12 muestra, para los tres terremotos con un periodo de retorno de 2475 años, la variación con la profundidad de la deformación de corte máxima, la relación G/Gmáx y la relación de amortiguamiento en cada una de las etapas de iteración del cálculo. El proceso de cálculo se efectuó hasta alcanzar la convergencia, que en ningún caso requirió más de 8 ciclos de iteración. Se puede observar cómo en una primera etapa de iteración, la relación G/Gmáx es igual a 1, y la relación de amortiguamiento toma valores bajos, correspondientes a niveles de deformación bajo, y a medida que se van realizando las demás iteraciones, las distribuciones de la relación G/Gmáx y la relación de amortiguamiento convergen hacia sus valores finales.

Además, se muestra el esfuerzo cortante máximo y la aceleración máxima convergente en cada uno de los estratos, durante las iteraciones; en ellos podemos observar la influencia de la carga sísmica en los valores finales del módulo de corte, amortiguamiento y esfuerzo de corte máximo, es decir, que independientemente de la máxima aceleración esperada en roca los valores de las propiedades del suelo se ven influenciado por el tipo de movimiento sísmico. 

La Figura 13 muestra los tres terremotos con un periodo de retorno de 2475 años, las historias de tiempo calculadas de aceleración, velocidad y desplazamiento relativo con respecto a la superficie libre.

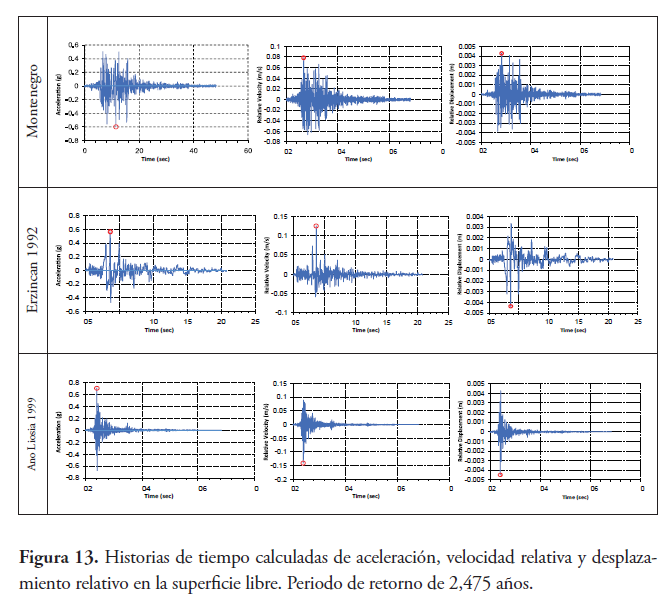
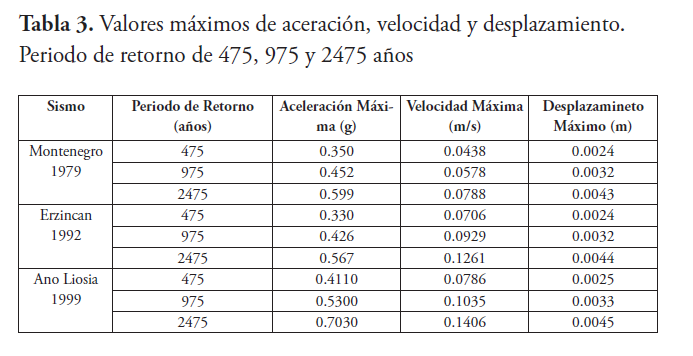
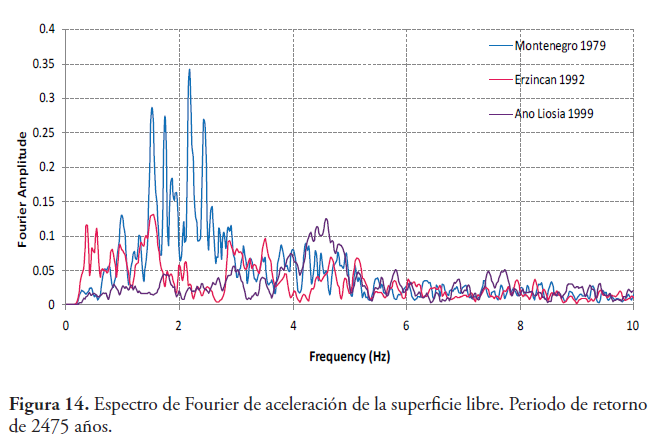
El desplazamiento relativo y la velocidad se evalúan con relación a la parte inferior del perfil del suelo. Obteniéndose para los diferentes periodos de retorno los valores máximos que se observan en la table 3. La Figura 14 muestra, para los tres terremotos con un periodo de retorno de 2475 años, el espectro de Fourier de la superficie libre (de salida). El espectro de Fourier es el producto de la función de transferencia que relaciona la base rocosa (movimiento de entrada) y la superficie libre, se puede observar la variación del contenido en frecuencia en función de la señal de entrada. 

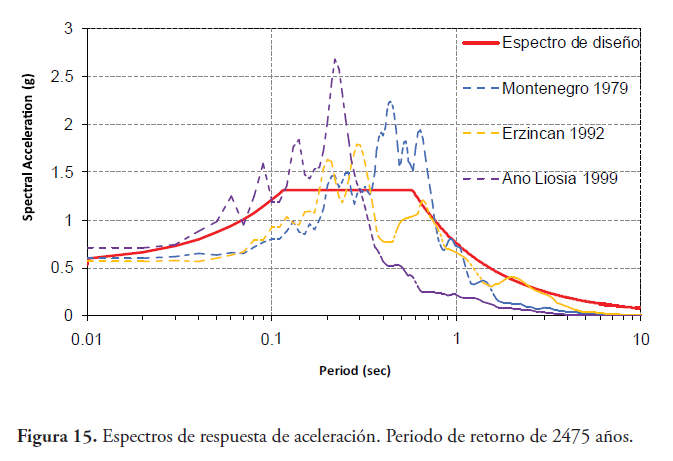
La Figura 15 muestra, para los tres terremotos con un periodo de retorno de 2475 años, los Espectros de respuesta de aceleración. Se puede observar que la máxima aceleración espectral es de 2.69 g, generada por el sismo de Ano Liosia (1999). Los valores de máximas aceleraciones espectrales, para los sismos analizados, se encontraron en un intervalo de período relativamente corto, de 0.18 a 1 segundos, donde se muestran valores muchos más altos que los considerados en las regulaciones de República Dominicana, los cuales deberían investigarse más a fondo. En cambio, para periodos entre 0.01 – 0.1 y 1 - 10 segundos se muestran resultados más acordes, que varían en función del movimiento de entrada.

8. Conclusiones

Se ha llevado a cabo un análisis de respuesta sísmica local en la presa Las Dos Bocas, basado en una aproximación lineal equivalente 1D del comportamiento no lineal del suelo y utilizando de entrada tres movimientos fuertes muy diferentes. Se puede observar que la respuesta está fuertemente influenciada no solo por la geología del sitio local, sino también por las características de los movimientos de entrada en sí. Los resultados de aceleraciones espectrales en la superficie comparados con las normativas en la República Dominicana muestran diferencias significativas; así, los resultados de este estudio evidencian valores más alto en el espectro de diseño para un rango de periodos. Hay que tomar en cuenta que las aceleraciones máximas esperadas en rocas no fueron tomadas de los reglamentos sísmicos del país, lo cual puede influenciar los resultados, sino que fueron obtenidas de estudios de amenaza sísmica realizados en diferentes proyectos (Proyectos Región Sur-Oeste) para distintas zonas, una de las cuales fue la presa Las Dos Bocas. Estos estudios dieron como resultados mayores aceleraciones esperadas en roca que las consideradas en la normativa sísmica. 

9. Reconocimientos

Esta investigación fue financiada por el Fondo Nacional para la Innovación y el Desarrollo Científico y Tecnológico (FONDOCyT). Estamos muy agradecidos por el apoyo recibido.