Un nuevo modelo analítico para balance térmico satelital

1. Introducción

El objetivo principal del subsistema de control térmico es mantener todo el subsistema de la nave espacial en el rango permitido durante toda la misión. El propósito del diseño térmico para un satélite es mantener todos los elementos del sistema de satélite dentro de los límites de su rango de temperatura para todas las fases de la misión. Además, para la evaluación del diseño térmico del satélite es necesario obtener la distribución de la temperatura de todos los componentes del satélite, mediante pruebas o análisis.

Este tipo de satélite se utiliza para vincular las comunicaciones vía satélite-Tierra, y consta de algunos subsistemas, como la batería, la computadora a bordo, la carga útil de comunicación, entre otros. Se asume que los paneles en forma de colmena son parte estructural del satélite. Para ilustrar la distribución de la temperatura del subsistema del satélite es necesario resolver la ecuación de energía transitoria para cada subsistema. Debido a que los subsistemas de las satélites y vehículos espaciales están acoplados térmicamente, se debe resolver un sistema de ecuaciones para encontrar la distribución de la temperatura de cada subsistema (Karam, 1998).

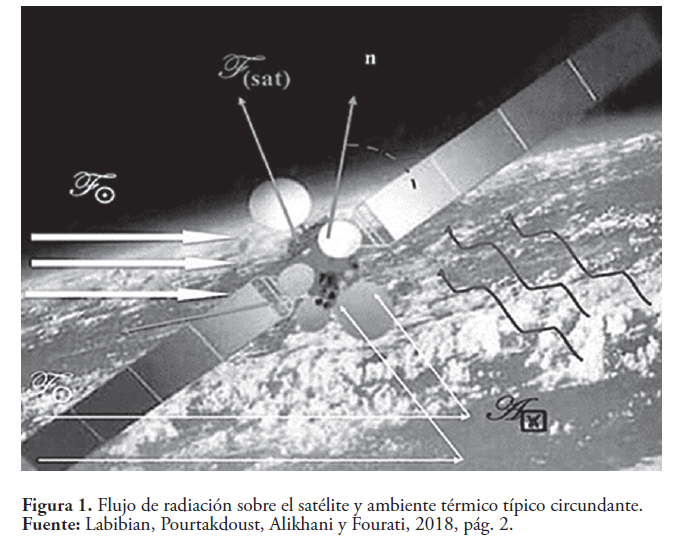
Una de las principales características del ambiente espacial es su alto vacío, por ello, para la mayoría de los satélites en órbita alta, la presión atmosférica residual y el arrastre resultante serán despreciables para el problema del balance térmico. Por lo tanto, el calentamiento aerodinámico y la interacción convectiva entre el satélite y el entorno espacial pueden ignorarse. Dado que la radiación es el medio clave del intercambio de calor en el espacio entre un satélite y su entorno, se puede caracterizar por los siguientes factores (Flujo Solar $F_{\odot }$, Albedo $A_{\odot }$, Radiación terrestre I_(IR)) son términos fuentes. (Ver Figura 1). (Labibian, Pourtakdoust, Alikhani y Fourati, 2018).

2. Metodología

Proponemos estudiar la transferencia de calor en las condiciones del ambiente espacial para un satélite geoestacionario, a través de la formulación analítica del problema de propagación del calor, sin asumir la hipótesis del equilibrio térmico.

El modelo matemático térmico para el satélite en órbita GEO es una descripción o representación matemática del problema de la transferencia de calor físico en forma de ecuación diferencial, basada en leyes físicas relevantes y haciendo algunas suposiciones y aproximaciones. La ecuación de energía que consiste en un término transitorio de conducción y de radiación más condiciones de frontera, es la ecuación que modela la distribución de temperatura de cada subsistema.

(Flujo Solar $F_{\odot }$, Albedo $A_{\odot }$, Radiación terrestre I_(IR)) son términos fuentes. (Ver Figura 1). La ecuación de energía general (Tsai, 2004) se escribe como:

$C\frac{dT}{dt}={\mathfrak{Q}}_{abs}+{\mathfrak{Q}}_{power} - \epsilon A\sigma T^4$  (1)

Además, la ecuación de energía general (2) se reduce a un cuerpo simplificado (con una conducción de calor despreciable) hacia el ambiente espacial y entorno, tales como el espacio profundo o una pared de la cámara de vacío térmico:

$\epsilon A\sigma T^{4 }={\mathfrak{Q}}_{abs}+{\mathfrak{Q}}_{power}$                (2)

donde $\epsilon A\sigma T^4$ puede obtenerse a partir de la suma de la energía de radiación absorbida ${\mathfrak{Q}}_{abs}$ por el cuerpo del ambiente y la disipación de potencia interna ${\mathfrak{Q}}_{power}$ en estado estable, es decir:

$C_p\frac{dT}{dt}=\epsilon A\sigma {T_E}^4 - \epsilon A\sigma T^4$                 (3)

Cuando la temperatura T está cerca de la temperatura de equilibrio T_E, la ecuación (2) se puede expresar aproximadamente como:

$\frac{dT}{dt}=\frac{1}{{\mathcal{t}}_{rad}}\left(T_E-T\right)$                          (4)

donde

${\mathcal{t}}_{rad}=\frac{C_p}{4\epsilon A\sigma {T_E}^3}$                                (5)

es el tiempo de ajuste térmico en pleno enfoque radiativo.

Nótese que la constante temporal es una medida de la rapidez con que la temperatura se aproximará a su valor de equilibrio. La solución de la ecuación (4) se puede obtener como:

$\frac{T}{T_E}=1+\left(\begin{array}{c}\frac{T_0}{T_E}\end{array}-1\right){\mathcal{e}}^{\frac{t}{t_{rad}}}$                  (6)

Podemos ver que en la ecuación (2) el modelo estándar asume que la temperatura efectiva del cuerpo negro es la misma temperatura termodinámica, pero no es cierto del todo, ya que en general el tiempo característico (tiempo orbital) es del orden del tiempo de la temperatura de ajuste, por lo tanto, el satélite no alcanza el equilibrio térmico.

Nuevo modelo analítico

$m{c}_p\frac{dT}{dt}={\mathfrak{Q}}_{abs}+{\mathfrak{Q}}_{power}-{\left(FA\right)}^{rad}$       (7)

La consideración habitual es asumir el equilibrio térmico, pero no es cierto, en general la intensidad radiada es:

$I^{rad } = A\mathcal{k}\stackrel{\rightharpoonup }{\nabla }\approx \frac{A\mathcal{k}}{R}\left(T-T_E\right)$                 (8)

donde utilizamos un satélite esférico, con R (dimensión característica) como el radio del satélite y T_E es la temperatura ambiente (temperatura típica del espacio exterior) resultando en:

$p{c}_{p}V\frac{dT}{dt} = \epsilon A\sigma T^4 - \frac{\mathcal{k}A}{R}\left(T-T_E\right)$      (9)

Esta ecuación se puede escribir como:

$\frac{dT}{dt}+\frac{T}{{\mathcal{t}}_{adj}}=\alpha T_E$                              (10)

donde

$$\begin{gathered} \alpha =\left[\begin{array}{c}\frac{\epsilon \sigma A{T_E}^3}{\rho c_{p}V}\end{array}+\frac{\mathcal{k}A}{\rho c_{p}VR}\right] \\ y \\ \frac{1}{{\mathcal{t}}_{adj}}=\left[\frac{\mathcal{k}A}{\rho c_{p}VR}\right] \end{gathered}$$

La solución de la ecuación (10) se puede obtener como:

$\frac{T}{{T_E}^{*}}=1-\left(\begin{array}{c}\frac{T_0}{{T_E}^{*}}\end{array}-1\right){\mathcal{e}}^{\frac{t}{{\mathcal{t}}_{adj}}}$               (11)

donde

${T_E}^{*}\equiv \alpha {\mathcal{t}}_{adj}{T}_E$                                (12)

Claramente, para tiempo mayor que el tiempo de ajuste, alcanza el equilibrio térmico y ${T_E}^{*}$ es aproximadamente$T_E$, entonces la ecuación (11) es una generalización de la ecuación (6), pero sin asumir la hipótesis del equilibrio térmico. Hay otro enfoque en el modelo estándar, en el que no es necesario verificar la realidad porque se ha asumido que el flujo de radiación solar es constante sobre el satélite.

Es bien sabido que la órbita del satélite alrededor de la Tierra también se eclipsa y tiene el ángulo de inclinación con respecto al flujo solar y cambia continuamente:

${\mathfrak{Q}}_{abs} = I_{sun}A\left(1+\cos \theta \right)=2I_{sun}{\cos }^2\left(\frac{\omega t}{p}\right)$ (13)

donde: $\omega , p, I_{sun}$, son la velocidad angular, el período y la constante solar, respectivamente. 

Como el cálculo anterior obtenemos: 

$\frac{dT}{dt}+\frac{T}{{\mathcal{t}}_{adj}}=a_{1 }- a_2\left[1-\frac{{\pi }^2{t}^2}{2p^2}\right]$         (14)

Usando el supuesto de que $\mathcal{t}<<p$ y usando la aproximación de Taylor para la función coseno, definimos:

$a_1= \left[\frac{\left(L_{\oplus }+ L_{sun}\right)}{pV{c}_p}\right] y a_2=\left(\begin{array}{c}\frac{L_{sun}}{pV{c}_p}\end{array}\right)$  (15)

La solución de la ecuación (14) se puede obtener como:

$$\begin{gathered} T_{\left(t\right)}=T_0 + \left[\left(a_1+a_2\right){\mathcal{t}}_{adj}+\frac{a_{1{\pi }^2{\mathcal{t}}_{adj}}}{2p^2} \left(t^2+2{\mathcal{t}}_{adj}t+2{{\mathcal{t}}^2}_{adj}\right)\right]- \\ -\left[\left(a_1+a_2\right){\mathcal{t}}_{adj}+\frac{a_1{\pi }^2{\mathcal{t}}_{adj}}{2p^2}\right]{\mathcal{e}}^{\frac{t}{t_{adj}}} \end{gathered}$$     (16)

3. Resultados y discusión

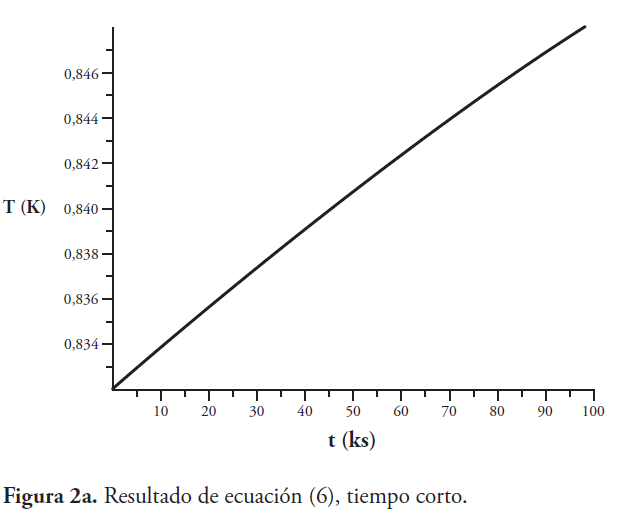
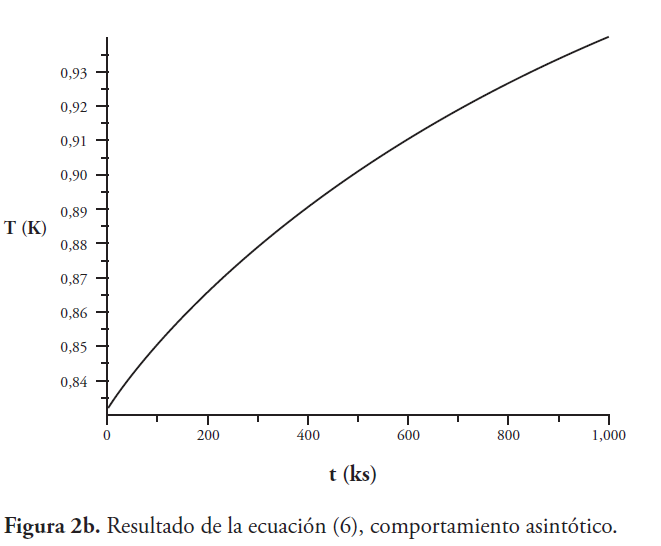
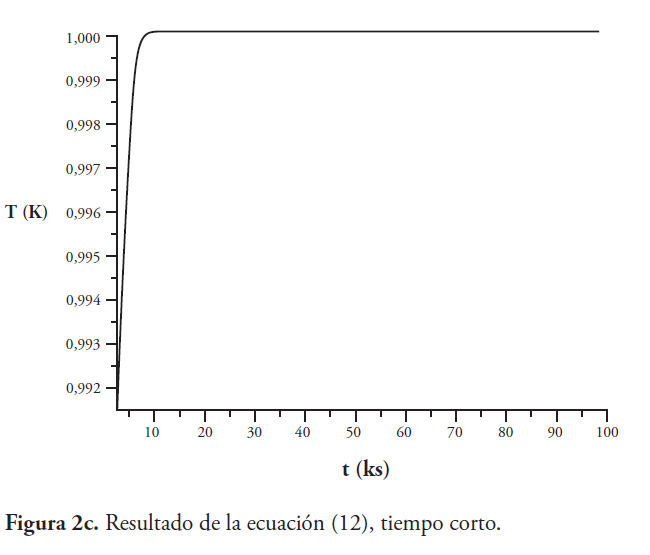
Ahora se muestra como ejemplo la estimación del tiempo de equilibrio térmico, a fin de comparar el modelo de equilibrio dado por la ecuación (6) con el modelo corregido dado por la ecuación (11) como se muestra en las Figuras 2a, 2b, 2c y 2d. Se ha hecho una estimación aproximada de los parámetros físicos del satélite Venesat-1 y, sin perder generalidad, se supone para todos los casos que la temperatura inicial del sistema es cero grados Celsius.

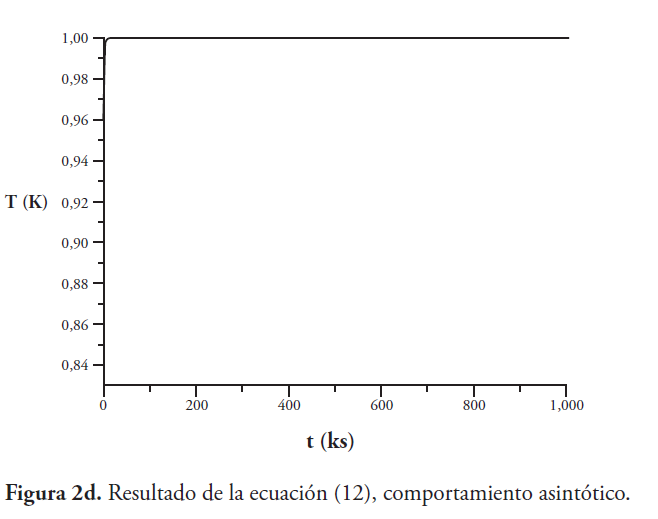
4. Conclusiones 

En las Figuras 2a, 2b, 2c y 2d, el tiempo está en kilo segundo; usando la ecuación (6) y la ecuación (11). En ambos casos, tiempo corto y comportamiento asintótico, notamos que la temperatura termodinámica alcanza un valor superior en el equilibrio, pero es más baja en el nuevo modelo analítico.

El modelo basado en el balance radiativo (Tsai, 2003; Karam, 1998) utiliza el método de igualar la temperatura efectiva, a través de la ley de Stephan-Boltzmann, con la temperatura termodinámica, la equivalencia solo es válida después de alcanzar el equilibrio térmico, pero utilizando la ecuación (5), el tiempo de ajuste radiativo es tan grande como 106 segundos; es decir, un período mucho mayor que el período orbital de los satélites geoestacionarios (GEO), por lo tanto, nunca alcanza el equilibrio. La paradoja se deriva de la suposición de que la temperatura efectiva es la temperatura termodinámica. Por otra parte, el tiempo de ajuste calculado en la ecuación (12) es solo 1710 segundos, es decir, tan pequeño como una centésima parte del período orbital de un GEO. En consecuencia, la temperatura de equilibrio, de 329 k, se alcanza en poco tiempo en correspondencia con la ecuación. (11).

Agradecimiento: se reconoce la colaboración de la Agencia Bolivariana para Actividades Espaciales (ABAE) en el suministro de la información técnica. Se agradecen las observaciones y sugerencias del Dr. Wang Jun, de la Universidad de BUAA (República Popular China).