LA LÓGICA DIFUSA APLICADA AL SECTOR MANUFACTURERO

1. Introducción

La lógica es el estudio de la validez de un argumento. La lógica clásica o bivalente fue desarrollada por Aristóteles y reconoce solo los valores de verdad verdadero o falso para cualquier proposición. En 1920 Jan Lukasiewicz propuso una lógica trivalente para incluir proposiciones verdaderas, falsas e indeterminadas. Luego a inicios de 1930 desarrolló una lógica de infinitos valores y tras ese esfuerzo se han desarrollado las lógicas polivalentes o multivaluadas.

Una de estas lógicas polivalentes es la lógica difusa desarrollada en 1965 por Lofti Zadeh, quien le asigna a una proposición grados de verdad, los cuales pueden ser absolutamente verdaderos, absolutamente falsos o con algún grado de verdad intermedio. Zadeh la definió como “un sistema que proporciona una vía natural para tratar los problemas en los que la fuente de imprecisión es la ausencia de criterios claramente definidos de tipos de pertenencia”.

La lógica difusa puede caracterizarse por ser una lógica polivalente especial que aborda el fenómeno de la vaguedad, desarrollando el aparato matemático para su modelización a través de grados de verdad en correspondencia con una escala ordenada. Esta lógica trata de preservar muchas propiedades de la lógica clásica. (Novak, 1990).

La vaguedad (imprecisión) es un concepto opuesto a la exactitud que surge de la forma como vemos el mundo y los fenómenos. La conceptualización de las ideas se realiza por medio de una idealización, sin embargo, la realidad desborda cualquier aproximación conceptual que tengamos sobre ella.

Por ejemplo, podemos distinguir los pequeños números de los grandes números, pero no podemos afirmar sin ambigüedad si cada número es pequeño o no. La propiedad “pequeño” es vaga y tiene que definirse en referencia a un contexto.

Para medir el índice de confianza industrial y el índice de clima empresarial, la información que se obtiene no es precisa, lo cual justifica el uso de la matemática difusa para obtenerlo. La lógica difusa tiene una correspondencia (isomorfismo) con la teoría de conjuntos. Veamos primero de forma preliminar algunos aspectos sobre la teoría de la matemática difusa.

2. Preliminares

TEORÍA DE CONJUNTOS DIFUSOS

Definición 2.1. Sea $X$ el conjunto universal. Un conjunto difuso o borroso $A$ en $X$ está identificado por su función de pertenencia,$\mathit{\mu }A\mathit{:}\mathit{}X\mathit{}\mathit{\to }\mathit{}\mathit{[}\mathit{0}\mathit{,}\mathit{1}\mathit{]}$, que asocia a cada punto en $X$ un número real en el intervalo $[0,1]$. El valor $A\left(x\right)=\mu A\left(x\right)$ es llamado grado de pertenencia de $x$ a $A. \left[14\right]$

OPERACIONES SOBRE CONJUNTOS BORROSOS

Sea $X$ el universo de discurso y sean $A\mathit{ }\mathrm{y}\mathit{ }B$ dos subconjuntos borrosos con funciones de pertenencia $\mathit{}{\mathit{\mu }}_{\mathit{A}}\mathit{\left(}x\mathit{\right)}\mathit{ }\mathit{ }\mathrm{y}\mathit{}{\mathit{\mu }}_{\mathit{B}}\mathit{\left(}\mathit{x}\mathit{\right)}$, respectivamente. Pueden definirse las siguientes operaciones:

Estas maneras de definir la intersección y la unión constituyen una generalización de los conjuntos clásicos, aunque estas no son las únicas generalizaciones. Existe una amplia clase de funciones conocidas como t-normas y t-conormas para la intersección y la unión, respectivamente. Dado que la intersección y la unión no son operaciones únicas, contrario a los conjuntos clásicos, diferentes funciones pueden ser apropiadas para representar estas operaciones en diferentes contextos.

Definición 2.2. Una t-norma es una función $\ast :[0,1]\times [0,1]\to [0,1]$ que satisface los siguientes axiomas:

•Límite condicional para la intersección $* (a, 1) = a$

•Monotonía para la intersección $* (a, b) \le * (c, d) si a \le c y b \le d$

•Conmutatividad para intersección $* (a, b) = * (b, a)$

•Asociatividad para la intersección $* (a, * (b, c\left)\right) = * ( * (a, b), c))$

Definición 2.3. Una t-conorma es una función $\bigsqcup :[0,1]\times [0,1]\to [0,1]$ que satisface los siguientes axiomas:

•Límite condicional para la intersección $\bigsqcup (a,0)=a$

•Monotonía para la intersección $\mathit{\bigsqcup }\mathit{}\mathit{(}a\mathit{,}\mathit{}b\mathit{)}\mathit{ }\mathit{\le }\mathit{\bigsqcup }\mathit{}\mathit{}\mathit{(}c\mathit{,}\mathit{}d\mathit{)}\mathit{}si\mathit{ }a\mathit{ }\mathit{\le }\mathit{ }c\mathit{ }y\mathit{ }b\mathit{ }\mathit{\le }\mathit{ }d$

•Conmutatividad para intersección $\bigsqcup (a,b)=\bigsqcup (b,a)$

•Asociatividad para la intersección $\bigsqcup (a, \bigsqcup (b,c\left)\right)= \bigsqcup ( \bigsqcup (a,b),c)$

Ejemplos de las t-normas y t-conormas más conocidas que sirven como una interpretación generalizada de la intersección y la unión son:

Definición 2.4. Una función $\Rightarrow :\left[0,1\right]\times \left[0,1\right]\to \left[0,1\right]$ es el residuo de una t-norma si cumple la siguiente condición:

$*(x,z)\le$ y si y solo si $z\le (\Rightarrow (x,y\left)\right)$ para todo $x,y,z\in [0,1]$

Las funciones anteriormente descritas utilizadas para operaciones entre conjuntos tienen sus correspondientes funciones en la lógica difusa. Así la t-norma corresponde a la conjunción, la t-conorma a la disyunción y el residuo a la implicación. A través del residuo podemos definir la negación y luego los demás conectivos lógicos.

Definición 2.5. Sea $A$ un conjunto borroso definido en el conjunto $\mathrm{ℝ}$ de los números reales, esto es, $A: \mathrm{ℝ} \to [0,1].$ A es llamado número borroso si cumple con las siguientes propiedades:

1) A debe ser un conjunto borroso normal, i. e $\exists x\in \mathrm{ℝ}$ tal que $A\left(x\right)=1;$

2) El corte alfa de $A$, definido como el conjunto $A\alpha = \{x | A\left(x\right) = \alpha \}$, donde $a$ $\in [0,1]$, debe ser un intervalo cerrado para cada $a$ $\in [0,1]$;

3) El soporte de A, definido como el conjunto $\left\{x\right|A\left(x\right)>0\}$, debe ser acotado.

El concepto de número difuso es una herramienta muy útil en las aplicaciones de conjuntos difusos y lógica difusa. Casos especiales de números difusos incluyen los números reales y los intervalos de números reales. Entre los números difusos ampliamente usados en determinadas aplicaciones tenemos el triangular, el trapezoidal y el gaussiano.

NÚMERO DIFUSO TRIANGULAR

Un número difuso triangular es especificado por una tripleta ordenada $\left(a,m,b\right)$con $a\le m\le b$ y su función de pertenencia es:

NÚMERO DIFUSO TRAPEZOIDAL

Es un cuádruple ordenado$(a,b,c,d)$ con $a\le m\le b\le c\le d.$ La función de pertenencia para un número difuso trapezoidal es:

NÚMERO DIFUSO GAUSSIANO

Los números difusos gaussianos son parametrizados por la media $m$ y la función de pertenencia es: $exp(-k(x-m{)}^2)$.

VARIABLE LINGÜÍSTICA

El concepto de número borroso es de suma importancia para formular variables cuantitativas borrosas, es decir, variables cuyos estados son números borrosos. Además, cuando los números borrosos representan conceptos lingüísticos como pequeño, muy pequeño, alto, etc., interpretados en un contexto particular, la variable resultante es llamada variable lingüística.

Definición 2.6. Una variable lingüística es un quíntuplo $\langle v, T\left(X\right), x, g, m\rangle$ en donde:

$v:$ Es el nombre de la variable lingüística.

$T\left(x\right):$ Ees el valor de la variable lingüística $x$

$X$: Es el universo del discurso o variable base

$g:$ Es una regla sintáctica de los términos lingüísticos $T$

$m:$ Es una regla semántica que le asigna a cada valor de la variable lingüística su significado en el universo del discurso $X$, es decir, es una función $T\to f\left(X\right)$.

Un ejemplo de una variable lingüística es 〈edad, $T\left(x\right),X,g,m⟩$

$v:$ Edad

$T\left(x\right)$ Joven, muy joven, muy muy joven, etc.

$X=[0,100]$ Es el universo del discurso para edad

$$\begin{gathered} m T\to f\left(X\right), M\left(joven\right)=conjunto difuso, \\ M (muy joven)=conjunto difuso \end{gathered}$$

LA MODELACIÓN DIFUSA

Es la aplicación de la lógica difusa y la teoría de conjuntos difusos para modelar fenómenos a través de reglas difusas. Por ejemplo, en procesos de control y toma de decisiones se podrían aplicar sistemas difusos. Un sistema difuso consta de cuatro fases: Fuzificación, bases de reglas difusas, inferencia y desfuzificación.

La fuzificación es la primera fase donde se establece una función desde $X$ a todos los conjuntos borrosos en $X$. En otras palabras, a un número real $x\in X$ se le asigna un grado de pertenencia a un conjunto borroso $A$. Luego están las reglas difusas que es una colección de reglas que describe la relación entre las acciones y los estados del sistema. Las reglas están expresadas en la forma si $\left(A_1\right)y/o\left(A_2\right)\dots \left(An\right)entonces\left(C_n\right)donde\left(A_n\right)y\left(C_n\right)$ son las acciones y los estados del sistema respectivamente para $n \in N$. En tercer lugar está la inferencia que es una regla de deducción para determinar una salida difusa basada en un conjunto arbitrario en $X$, y por último, la idesfuzificación que es un operador que transforma conjuntos borrosos a números reales. Existen varios métodos de desfuzificación siendo uno de los más utilizados el centro de gravedad.

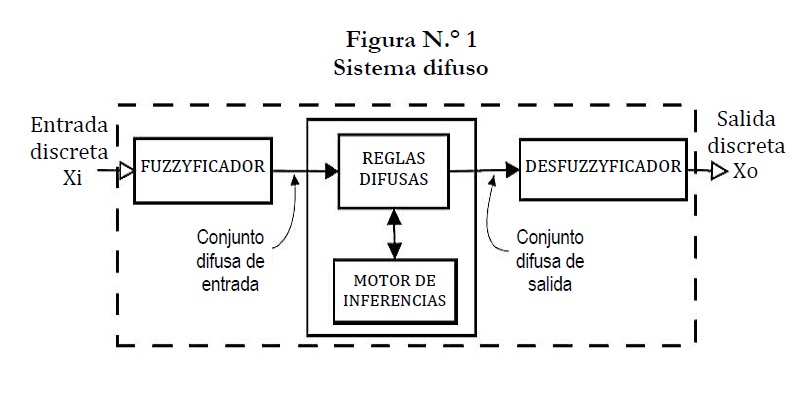
3. Métodos y técnicas en el estudio

Los datos provienen de la Encuesta Nacional de Opinión Empresarial del Sector Manufacturero que realiza el Banco Central de la República Dominicana correspondiente al primer trimestre de 2011. El estudio se realizó con una muestra de 293 empresas (60% aleatorias y 40% obligatorias, para cumplir con la representatividad en la rama de actividad del sector), y se entrevistó al personal de gerencia del sector manufacturero, excluyendo las empresas estatales, las zonas francas y las industrias azucareras. 

Realizaremos un análisis comparativo entre los saldos de opinión de las variables y la medida de consenso propuesta por Tastle y Wierman, que es una medida de dispersión para datos ordinales. Las medidas de consenso y saldos de opinión serán los parámetros de cuatro sistemas difusos para medir el índice de confianza industrial y el índice de clima empresarial que representarán las opiniones del empresariado respecto a la situación económica de sus empresas y de la economía, en general, respectivamente. Luego se comparan los índices de los sistemas difusos con los índices calculados mediante la metodología del promedio de los saldos de opinión que tiene como base una escala tipo Likert con tres categorías (mayor, igual y menor) utilizada en la encuesta.

Para la realización de los modelos difusos utilizaremos el paquete informático Matlab. 

La escala tipo Likert es una escala ordinal donde la suma no está permitida, sin embargo es utilizada como una escala razón que tiene la propiedad de ser aditiva. Esto significa que la media y la desviación estándar no son estadísticos apropiados como medida de tendencia central y de dispersión de la escala. (Qing Li y Cheryl, 2010). 

Una medida de dispersión para datos ordinales es la establecida por Tastle y Wierman para medir el consenso. El consenso es definido como una opinión o posición alcanzada por un grupo de personas como acuerdo general. (Tastle y Wierman, 2007). La medida de consenso es definida como:

Donde $X$ es la escala Likert, pi es la probabilidad de cada X, d es la profundidad de $X$, $i.e.d=Xmax-Xmin, x_i$i es un atributo particular de $X$ y u es el valor esperado. Podemos fijar el valor del consenso de una pregunta respecto a una categoría de la escala para calcular la fuerza del consenso en este punto. Para ello utilizamos la fórmula anterior fijando la media en 1 y duplicando la distancia. (Tastle, J. y Tastle, W. 2005).

4. Modelos

MODELOS PROPUESTOS

Proponemos el desarrollo de dos modelos difusos para medir el índice de confianza industrial (ICI) y dos sistemas difusos para el índice de clima empresarial (ICE). El método de inferencia para los modelos propuestos es el tipo Mandani, que es el más utilizado y fue introducido por Mandani y Assilan en 1975. (Sivanandam, Sumathi, y Deepa, 2007). El método de fuzificación utilizado es el max-min y el de desfuzificación es el centro de gravedad.

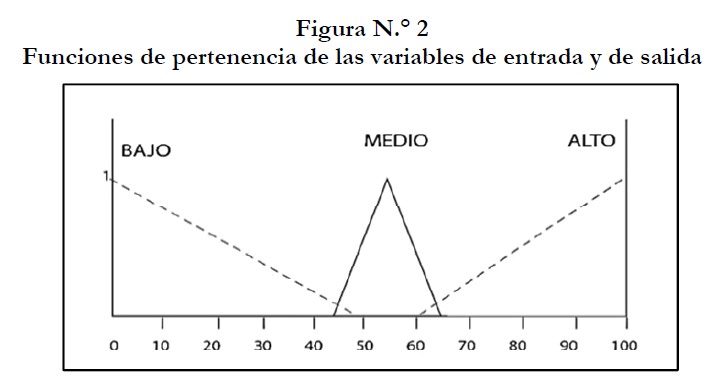
FUNCIONES DE PERTENENCIA

Variables de entrada

Las funciones de pertenencia usadas son las triangulares. La obtención de las funciones de pertenencia puede realizarse a través de criterios de expertos o algoritmos lógicos y en nuestro caso se ha elegido la primera alternativa. 

Para cada valor lingüístico de las variables se necesita una función de pertenencia o conjunto borroso y dado que todos los indicadores de nuestro sistema tenían el mismo rango (0 a 100) utilizamos los valores lingüísticos bajo, regular y alto para todos los indicadores.

BAJO

MEDIO

ALTO

Variables de salida

Para la variable de salida en cada uno de los índices utilizaremos los mismos valores lingüísticos bajo, medio y alto con las mismas funciones de pertenencia triangulares utilizadas como variables de entrada.

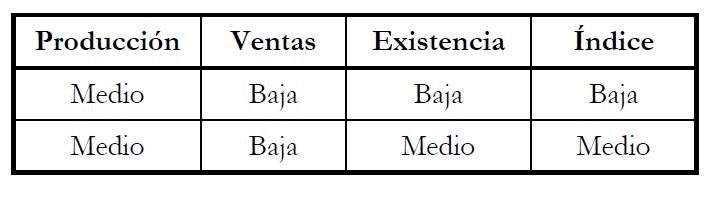
Las reglas difusas que utilizaremos, obtenidas a través de criterio de experto son:

5. Resultados

Un primer análisis fue realizado para calcular los saldos de opinión que indican el resultado de un indicador particular y se mide como la diferencia entre la categoría mayor y la categoría menor de una escala tipo Likert de tres categorías. Por ejemplo, a la pregunta de si la producción para el próximo trimestre aumentará, disminuirá o permanecerá igual con una distribución de probabilidad $p\left(1\right) = 0.21, p\left(2\right) = 0.43 y p\left(3\right) = 0.35$, el saldo de opinión es $-0.14 (-14 \%)$. Este resultado indica que aquellos que opinaron que la producción será menor para el próximo trimestre excedieron en 14% a aquellos que opinaron que la producción será mayor, y por tanto, esta es la tendencia. El cuadro N.◦ 1 muestra los valores del saldo de opinión y la fuerza del consenso en la categoría mayor para cada una de las variables, además de la media aritmética y la desviación estándar, respectivamente.

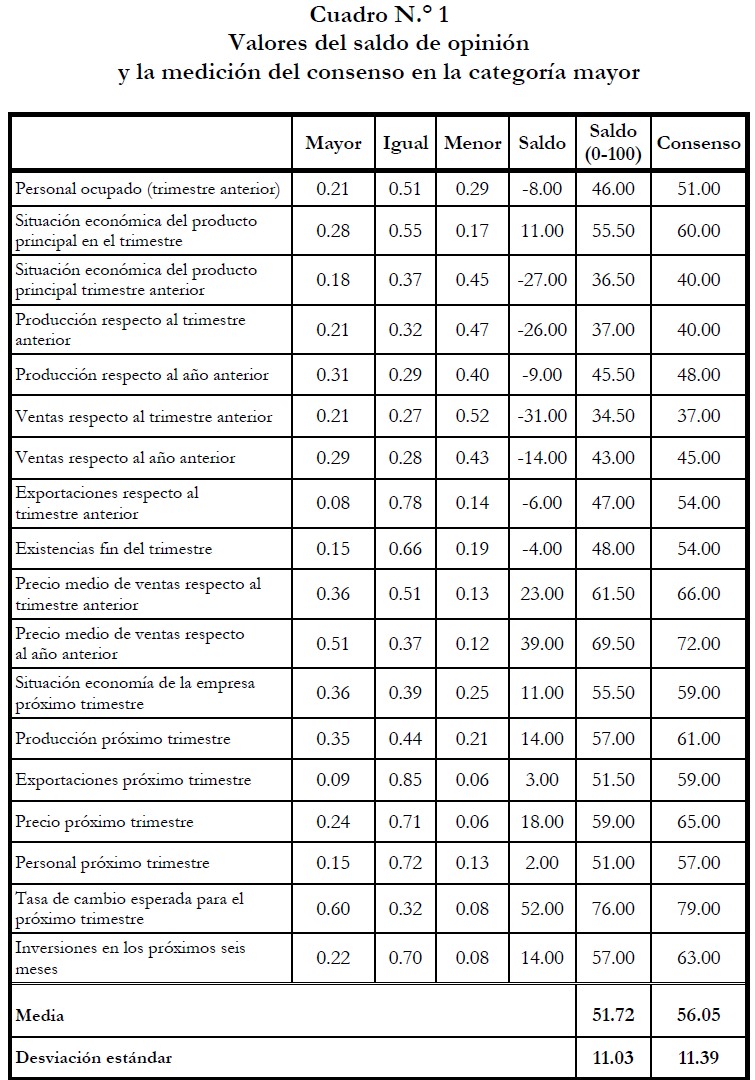
Una propiedad importante que debemos considerar con relación a las escalas de medición es la invariancia debido a que determina la generalidad de las afirmaciones respecto a la medición. Al comparar ambas escalas se observa que las medidas de consenso permanecen invariante a transformaciones multiplicadas por un escalar, preservando el orden y las proporciones. Los saldos de opinión no mostraron la propiedad de invarianza, debido a que al multiplicarse por un escalar no preservan el orden, sin embargo, al transformarse la escala sí mostraron la propiedad de invarianza.

ÍNDICE DE CONFIANZA INDUSTRIAL (ICIN)

Un primer sistema difuso fue realizado para medir el Índice de Confianza Industrial (ICIN) teniendo como parámetros en las variables de entrada los saldos de opinión. Las variables de entrada fueron la producción en el próximo trimestre, inventarios y ventas en el trimestre anterior. El sistema difuso reportó un Índice de Confianza Industrial de 46.51.¹ El Índice reportado por la metodología del promedio de los saldos de opinión² fue de 47.80. La figura N.◦ 3 muestra las fases del sistema difuso. 

En el proceso de fuzificación se obtiene el grado de pertenencia para cada una de las variables de entrada o parámetros del sistema y el conjunto borroso de la variable de salida. A cada variable de entrada le puede corresponder uno o más grados de pertenencia, dependiendo de si intercepta a uno o varios conjuntos difusos. En el ejemplo anterior, la variable existencia intercepta los conjuntos difusos bajo y medio, obteniéndose dos grados de pertenencia que luego se combinarán con las otras dos variables.

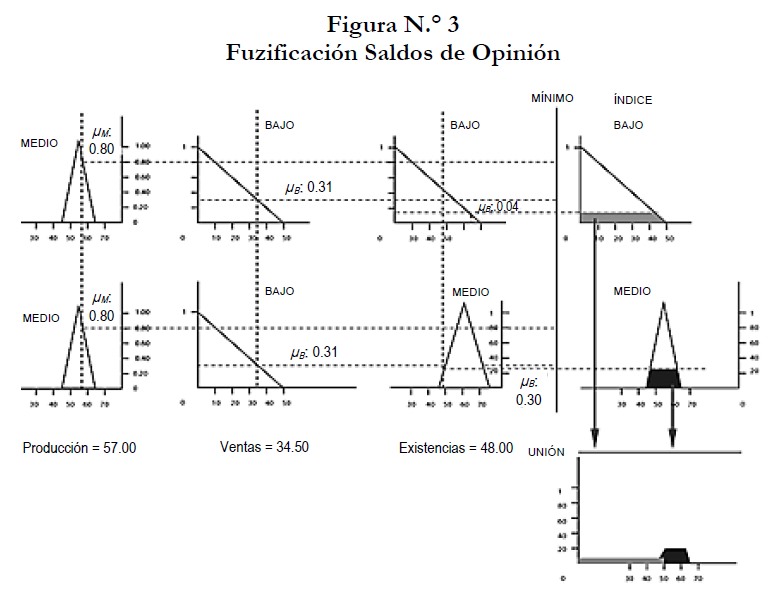
La combinación de los conjuntos borrosos se realiza utilizando el operador que hayamos seleccionado en nuestro modelo y las bases de conocimiento. En el caso anterior utilizamos el operador mínimo (intersección).

Los cálculos se realizaron de la manera siguiente:

Producción $\left(p\right) = 57.00$

ventas $\left(v\right) = 34.50$

Existencia$\left(e\right)=48.00$

Los grados de pertenencia que le corresponden a estos parámetros son:

${\mu }_p=0.80$para el conjunto borroso medio

${\mu }_v=0.31$ para el conjunto borroso bajo

${\mu }_e=0.04$ para el conjunto borroso bajo

${\mu }_e=0.30$ para el conjunto borroso medio

Para la intersección de conjuntos borrosos, utilizando las reglas según nuestra base de conocimiento tenemos:

Sea:

$B =$ conjunto borroso Bajo de la variable de salida

$M =$ conjunto borroso Medio de la variable de salida

Los conjuntos borrosos de la variable de salida, según nuestra base de conocimiento son:

Luego procedemos a su unión:

Este es el conjunto a desfuzificar. El procedimiento de defuzificación fue el centro de gravedad.

Un segundo sistema difuso fue realizado para medir el Índice de Confianza Industrial teniendo como parámetros en las variables de entrada las medidas de consenso. El Índice de Confianza Industrial fue de 55.00.

ÍNDICE DE CLIMA EMPRESARIAL

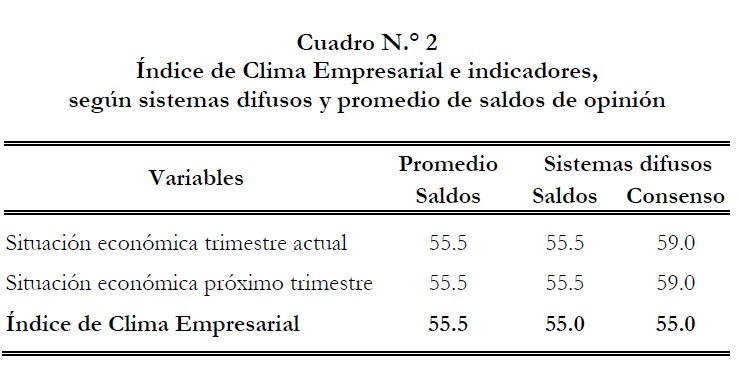
Un tercer y cuarto sistema difuso fue realizado con el fin de medir el Índice de Clima Empresarial. Las variables de entrada fueron la situación económica en el actual y próximo trimestre. Los sistemas difusos cuyos parámetros fueron los saldos de opinión y las medidas de consenso reportaron un Índice de Clima Empresarial de 55.00 y 55.00, respectivamente. El índice reportado por la metodología (promedio) de los saldos de opinión fue de 11.00 (según el Banco Central de la Republica Dominicana, 2011), calculado en una escala de -100 a 100. Si trasladamos dicho valor a una escala de 0 a 100 a través de una transformación lineal obtendríamos un Índice de Clima Empresarial de 55.50 (cuadro N.◦ 2).

6. Discusión y conclusiones

Los sistemas difusos desarrollados mostraron capacidad para medir de forma satisfactoria la confianza industrial y el clima empresarial. En el desarrollo de estos sistemas se utilizaron indicadores medidos a través de los saldos de opinión y las medidas de consenso.

Los resultados de los sistemas difusos se compararon con los resultados de la metodología que se utiliza en la encuesta que calcula el Índice de Confianza Industrial (ICIN) y el Índice de Clima Empresarial (ICE) como la media aritmética y la media geométrica de los saldos de opinión, respectivamente.

El Índice de Confianza Industrial del sistema difuso se realizó utilizando los parámetros medidos a través de los saldos de opinión fue de 46.40, mientras que el índice medido como la media aritmética de los saldos de opinión fue de 47.80.

La medición del mismo concepto se hizo utilizando un sistema difuso que tuvo como parámetros las medidas de consenso que fueron de 55.00. Es necesario señalar que las medidas de consenso fueron mayores que los saldos de opinión.

El Índice de Clima Empresarial calculado por los sistemas difusos fue de 55.00 y 55.00, utilizando los saldos de opinión y las medidas de consenso, respectivamente. El Índice calculado en la encuesta como la media geométrica de los saldos de opinión fue de 55.50.

Consideramos que el desarrollo de otros sistemas difusos utilizando otras funciones de pertenencias y/o reglas de conocimiento aportaría a la validez de los modelos desarrollados. La elegancia y la precisión de los sistemas difusos dependen de estos dos criterios. Los resultados obtenidos contribuirán a un mejor entendimiento de las opiniones y las actitudes de la clase industrial dominicana,

pues estas constituyen el marco de referencia para el diseño de políticas públicas (Russell, 2011). 

Los modelos difusos que se han desarrollado están sustentados en sólidos fundamentos teóricos que vienen a validar la metodología utilizada por el Banco Central de la República Dominicana. Esta metodología, a nuestro entender, utiliza la escala tipo Likert como una escala razón cuando en realidad es una escala ordinal que no es aditiva. 

En conclusión, la confianza del sector industrial en el primer trimestre del año 2011 utilizando sistemas difusos fue de 46.40 puntos, la cual puede calificarse como media. Para el índice de Clima Empresarial la puntuación fue en promedio de 55.00 puntos e igualmente puede calificarse como media.

Referencias bibliográficas

Banco Central de la República Dominicana. (2011). Encuesta Nacional de Opinión Empresarial al Sector Manufacturero. (Enero-marzo de 2011). Santo Domingo: Banco Central de la República Dominicana.

Guzmán, R., et al. (2011). 4 décadas de Políticas de desarrollo productivo en República Dominicana. Santo Domingo: Instituto Tecnológico de Santo Domingo.

Höhle, U. (1996). On the fundamentals of fuzzy set theory. Journal of Mathematical Analysis and Applications 201 [ARTICLE NO. 0285], 786-826.

Klir, G. (1995). Fuzzy sets and fuzzy logic. Theory and applications. New Jersey: Prentice-Hall.

Medina Hurtado, S. y Paniagua Gómez, G. (2008). Modelo de inferencia difuso para estudio de crédito. Dyna, 75(154), 215-229.

Novak, V. (1990). Which logic is the real fuzzy logic. Ostrava: Institute for Research and Applications of Fuzzy Modelling, University of Ostrava. [Research report No. 73].

Qing Li, Cheryl, L. (2010). A new likert scale based on fuzzy sets theory. Connecticut: University of Connecticut.

Ross, T. (2004). Fuzzy logic with engineering applications. (2da. Ed.). New Jersey: John Wiley & Sons Ltd.

Russell, B. (2011). El poder: Un nuevo análisis social. (5ta. Ed.). Barcelona: RBA Libros, S. A.

Sivanandam, S. N.; Sumathi, S., & Deepa, S. N. (2007). Introduction to fuzzy logic using MATLAB. Berlin: Springer-Verlag.

Tastle, W., & Wierman, M. (2007). Consensus and dissention: A Measure of Ordinal Dispersion. International Journal of Approximate Reasoning: 531-545.

Trillas, E., & Gutiérrez, R. (1992). Aplicaciones de la lógica borrosa. Madrid: Consejo Superior de Investigaciones Científicas.

Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 338-353.

Datos de filiación

Yamir Encarnación. Es licenciado en Economía (UASD). Tiene una maestría en Matemáticas (INTEC) y terminó la especialidad en Pensamiento Complejo, Ciencias de la Complejidad y Teoría del Caos (Instituto Global de Altos Estudios en Ciencias Sociales). Además fue fellow en metodología de encuestas en la Universidad de Illinois at Chicago (UIC). Laboró en la Dirección de Información, Análisis y Programación Estratégica del Poder Ejecutivo de la Presidencia de la República Dominicana en el diseño de encuestas y análisis de datos. Ha participado en investigaciones sociales y trabajó en El libro blanco del periodismo dominicano. El autor tiene interés de continuar aplicando la lógica difusa al área social y en el estudio de las ciencias de la complejidad.

Email: yamirencarnacion@gmail.com