1. Introducción
En esta investigación se estudia el comportamiento mecánico y fractal de materiales compuestos reforzados con cenizas volcánicas a través de métodos de la geometría fractal y ensayos mecánicos, fin de darles una aplicación tecnológica en el sector industrial. Cenarc, Cenepo y Cenpol son los compuestos que se analizarán. Cenarc tiene la matriz cerámica reforzada con polvo volcánico, cuya composición química es de 41% de C, 43% de O, 2% de Al, 11% de Si, 1% de K, 1% de Na y 1% de Pb átomos. Cenepo posee la matriz de resina epóxica reforzada con ceniza volcánica con un porcentaje atómico de elementos químicos de 67% de C, 26% de O, 1% de Al, 4% de Si, 1% de Ca y 1% de Na y Cenpol es un polímero poliéster reforzado también con ceniza volcánica, contiene un 74% de C, 24% de O, 1% de Al y 1% de Si (Soto, 2007).
Las cenizas utilizadas para reforzar las matrices de resinas y arcilla son residuos sólidos granulares que están constituidos por un polvo lávico menor de dos milímetros desprendido por el Volcán Popocatépetl, localizado en Estado de México, México (Peral, 2005), (Ortiz, et al., 1996). El compuesto Cenarc es el resultado de la combinación de las características de la ceniza con las de la arcilla a través del proceso de vitrificación, y los compuestos Cenepo y Cenpol resultan del desecho con las resinas epóxica y de poliéster particularmente. Asimismo, se determinaron las propiedades físicas y mecánicas de los compuestos basada en algunos principios de la física y en las ciencias de materiales; entre las propiedades físicas, tales como la porosidad, el grado de absorción de agua y la dureza, y las propiedades mecánicas de resistencia a la flexión y a la fatiga.
Las indagaciones que varias ciencias han hecho sobre diferentes fenómenos y casos de ingeniería, han encontrado situaciones que no han sido posibles de describir adecuadamente en forma tradicional (Balankin et al., 1996). Una característica común de estos casos provenientes de distintas ramas del conocimiento es que se trata de fenómenos no lineales (Balankin et al., 1997). Por ende, gracias al esfuerzo de varios científicos fundamentado en modelos teóricos, han mostrado que estos fenómenos poseen geometrías no-euclidianas y exhiben un comportamiento basado en parámetros de escala (Cherepanov et al., 1995) que se refleja en la identificación de objetos de una clase especial, llamados “fractales”. Los cuales son estructuras geométricas complejas y detalladas a cualquier nivel de magnificación cuya construcción, crecimiento o forma responde a reglas irregulares o de fragmentación, y que pueden ser caracterizadas por una dimensión fractal, que es diferente a la dimensión topológica y normalmente es fraccional (Olivares, 2002) y poseen la propiedad que permite que cada pequeña porción de un fractal puede ser visualizada como una réplica a escala reducida del todo (Ortega et al., 1996). Por lo tanto, basándose en los fundamentos de la mecánica fractal se llevara a cabo el estudio del comportamiento mecánico de estos compuestos debido a que estos materiales no se le puede hacer con facilidad un ensayo de fractura usando una muesca por ser materiales frágiles y anisotrópicos (Ortega et al., 1997). De modo que si se editan y compilan las imágenes del perfil de las superficies fracturadas a través de métodos de la geometría fractal y programas especializados, se pudiera obtener la dimensión fractal de las mismas (Balankin, 1996b), la cual se comparará con algunas de las propiedades mecánicas que poseen estos compuestos (Pérez, 1998). Para complementar el estudio, dicho comportamiento se podrá analizar a través de distribuciones de probabilidad (Askeland, 2006).
Los métodos y herramientas que se emplearon en los ensayos y los análisis se presentan a continuación.
2. Procedimiento experimental
De acuerdo al diseño de experimento para cada ensayo se utilizó un tamaño de muestra 30. Se empleó un diseño factorial 2k (Mendenhal et al., 1997), tomando en cuenta, los factores del tipo de material, la temperatura, composición y el tipo de matriz (Montgomery et al., 1991).
Se hizo un experimento físico para determinar el porcentaje de absorción de agua y la porosidad de cada uno de los compuestos con el propósito de determinar sus características estructurales (ASTM C373-88) (Farrington et al., 1997). Posteriormente, se realizó la prueba de microdureza Vickers, durante la cual se tomaron mediciones, aleatoriamente, en diferentes partes de cada espécimen empleando un microdurómetro Vickers Shimadzu modelo (CM 227-083) a fin de medir la resistencia que tienen las superficies a la ralladura (ASTM C 849-88).
Por otro lado, se realizó el ensayo de flexión en tres puntos, en el cual se determinó la resistencia a la flexión o módulo de ruptura y el módulo de elasticidad de cada uno de los materiales (ASTM C 674 8-88). En el ensayo, la carga de flexión se aplicó de manera perpendicular a la superficie del espécimen de prueba y se indujo la flexión obteniéndose los datos para calcular dichas propiedades. Posteriormente, se llevó el ensayo de fatiga aplicando una carga fija a modo de flexión en 4 puntos y frecuencia variable acorde a las normas (ASTM C 1360-96) y (ASTM C 1368-97).
Después se analizó la sección transversal fracturada de cada uno de los especímenes, empleando los programas: Paint, Scion Image (Scion Corporation, 2001), Benoit (Benoit, 1997) y @Risk (Palisade Corporation, 2002). Con Scion image, se evaluó la rugosidad de los perfiles después de ser convertidas en imágenes digitalizadas con formato de archivos BMP de Paint (figura N.° 1a) en archivos txt (figura N.° 1b).

Enseguida se empleó el programa Benoit para determinar el exponente de Hurst y la dimensión fractal de los perfiles de las superficies fracturada por flexión y fatiga. Los métodos fractales utilizados fueron trazas auto afines (Rango/Escalado, Variograma, Longitud-longitud) (Benoit, 1997). Por último, se empleó el programa @Risk para hacer el análisis probabilístico de los resultados del coeficiente de Hurst a fin de ayudar a seleccionar las distribuciones de probabilidad a que mejor se ajustan los valores de las propiedades.
3. Análisis de resultados
A continuación se presenta el análisis de los resultados del estudio realizado con los materiales compuestos reforzados con cenizas.
3.1 PROPIEDADES FÍSICAS DE LOS COMPUESTOS DE CENIZAS
En la tabla N.° 1, se presentan los valores de la porosidad aparente, porosidad real y el porcentaje de absorción de agua para los compuestos, los cuales se calcularon a partir de los datos de masas secas, masas suspendidas y masas saturadas de los especímenes obtenidos en el ensayo (ASTM C 373-88) (Kenett et al., 2000).
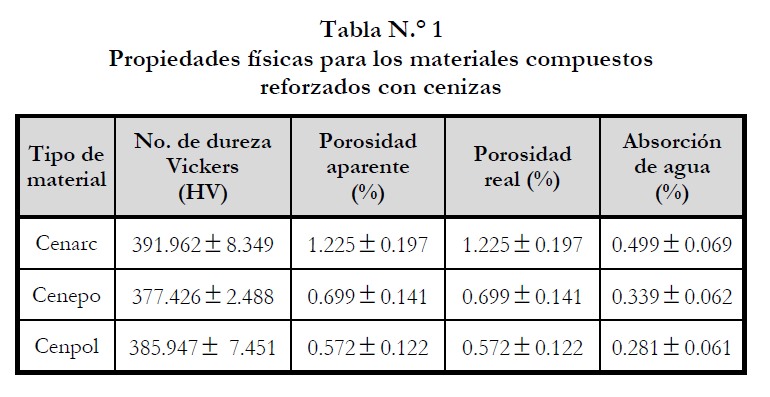
La porosidad aparente representa el contenido de huecos, que no es más que el volumen total de espacios de poros abiertos y la porosidad real es el porcentaje del volumen total constituidos por dichos huecos, tanto abiertos como cerrados (Shackelford, 1995), (Tani, 1999). En este contexto, el compuesto de matriz cerámica posee más poros que los otros compuestos debido a que la arcilla es un polvo granular de estructura porosa a diferencia de las resinas que son sustancias totalmente adheribles, elásticas y poco porosa (Bilurbina et al., 1990).
Los materiales compuestos tienen número de dureza Vickers muy cercanos entre sí, tal como se muestran en la tabla N.°1. Por su superficie vitrificada, Cenarc presentó mayor resistencia a la indentación en comparación con los otros dos compuestos de polimeros, siendo Cenepo el de la menor tenacidad (Soto, 2007). La dureza de estos materiales depende de las características de la matriz, el refuerzo y de la técnica empleada en el proceso de manufactura. No obstante, en la mayoría de los materiales, la dureza se incrementa a medida que se reduce el tamaño de partículas y depende también del tipo de enlace atómico de su estructuras y aumenta, en forma semejante a la resistencia, con la magnitud de las fuerzas atómicas (Jastrzebski, 1979), (Askeland, 2006).
3.2 MÓDULO DE ELASTICIDAD Y MÓDULO DE RUPTURA DE LOS COMPUESTOS DE CENIZAS
En la tabla N.° 2, se muestran los valores de deflexión, del módulo de elasticidad y de la resistencia a la flexión o módulo de ruptura de los compuestos de cenizas, los cuales fueron obtenidos por normativa (ASTM C 674-88).
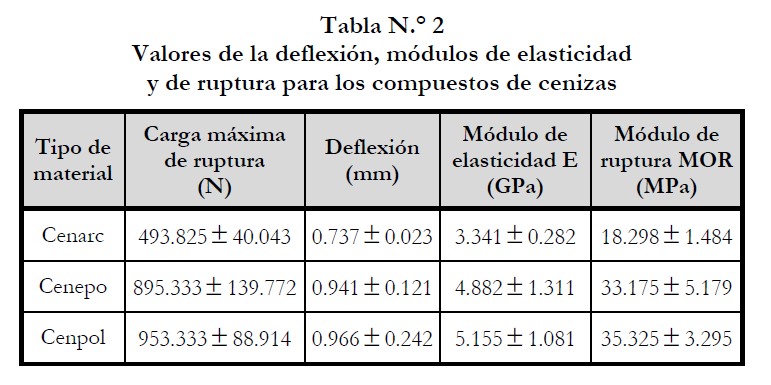
Por baja ductilidad en los compuestos, la carga aplicada por flexión produjo una falla que dio lugar a la deflexión (tabla N.° 2). La carencia de plasticidad se debe probablemente al tipo de enlace que poseen los materiales, los cuales pueden ser iónicos y/o covalentes de acuerdo a la naturaleza de las matrices y los refuerzos utilizados. En el caso de los materiales de matriz polímero, la baja resistencia se debe a los defectos microestructurales en las fronteras de granos originados durante el proceso de fabricación (Soto, 2007). La fractura de los especímenes de prueba puede observarse en la figura N.° 2, en las cuales se aprecia la rugosidad de las caras transversales que definen el perfil.

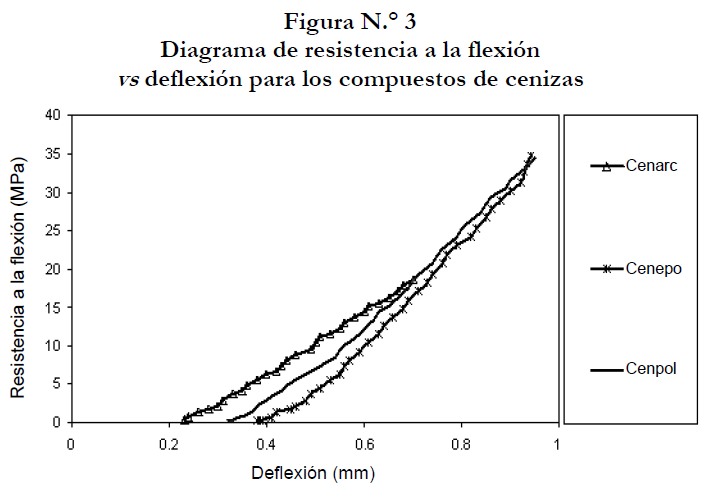
En general, el grado de fragilidad es lo que afecta la resistencia a la flexión de estos materiales. Cenarc presentó poca capacidad de deflexión bajo la carga aplicada; las fracturas se iniciaron en algunos poros de su superficie, en el cual se produjo una concentración de esfuerzos que dio lugar a la falla (Shackelford, 1995). Cenpol tiene una alta resistencia a la flexión ya que absorbió más energía en el límite elástico que los otros compuestos debido a sus propiedades adherencia y consistencia de la resina poliéster al aglomerar las cenizas. Características similares fueron presentadas en Cenepo. Sin embargo, Cenarc presentó poca capacidad de deformación debido a su tipo de estructura. En la figura N.° 3, se muestra el comportamiento mecánico de los compuestos a la flexión;
3.3 RESISTENCIA A LA FATIGA DE LOS COMPUESTOS DE CENIZAS
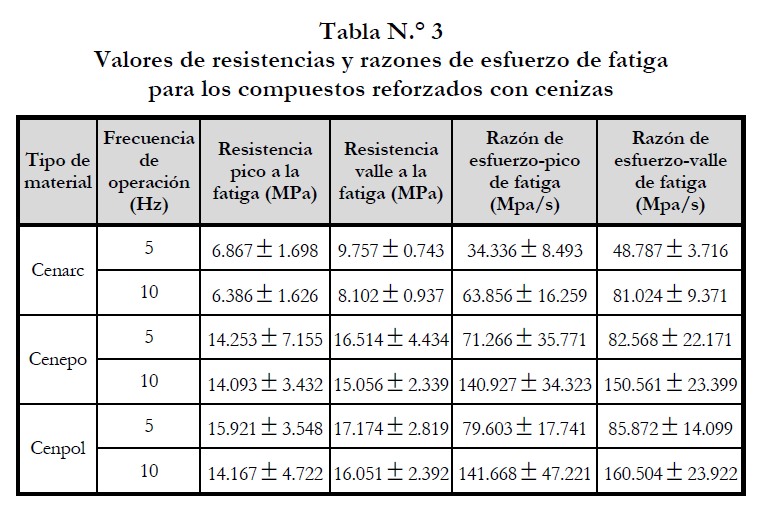
Los resultados obtenidos de la prueba de fatiga se presentan en la tabla N.° 3. Valores más altos de resistencia lo presentan los polímeros a mayor ciclaje.
El efecto de la carga cíclica, produjo grietas microscópicas en los centros de concentraciones de esfuerzo localizados en algunos huecos de las superficies de prueba, que en forma consecuente, condujo al crecimiento y la diseminación de una microgrieta hasta la falla. En los especímenes puede observarse que el área de fatiga suele ser más uniforme y lisa que el área de falla final, la cual presenta una textura mucho más áspera (figura N.° 4). En cada zona de la fatiga pueden distinguirse poros, lugares donde se originó la grieta.

Los compuestos que presentaron mayor resistencia a la fatiga a una frecuencia de 5 Hz tienen el perfil más curvo en la zona de fractura, tal como es el caso de Cenpol y Cenepo, respectivamente. En tanto los que muestran perfiles rectos son de más baja resistencia, en el caso de Cenarc (tabla N.° 3). Sin embargo, al aumentar la frecuencia de prueba, disminuyó la resistencia en estos materiales. En general, los materiales presentaron bajas resistencias a la fatiga durante el ensayo (tabla N.° 3). Al incrementar los ciclos operacionales se redujo la vida útil de estos compuestos. En la figura N.° 6, puede compararse la resistencia a la fatiga en función de la razón de esfuerzo para cada material.
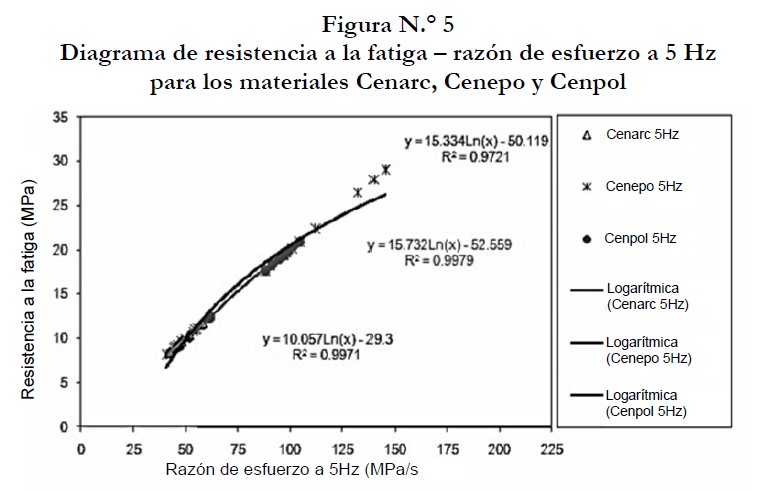
En la figura N.° 5, se observa que al someterse estos compuestos a una frecuencia de 5 Hz, la resistencia ante la razón de fatiga para cada material antes de llegar al límite de falla, sus trayectorias presentaron la forma de una curva logarítmica. No obstante, cuando se incrementó la frecuencia de aplicación de la carga, tuvieron un comportamiento en forma exponencial (figura N.° 6), y fueron disminuyendo su resistencia.
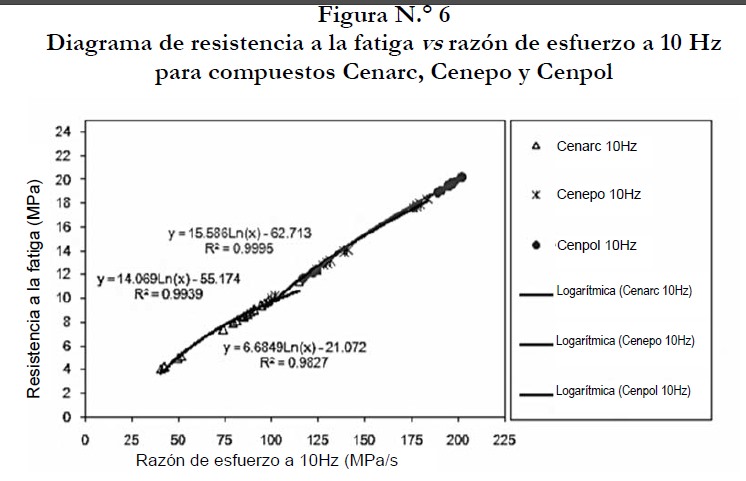
La resistencia a la fatiga se correlaciona con la resistencia a la flexión de tal manera que los que tienen mayor resistencia en carga estática también la tienen al variar la frecuencia, en el caso de Cenpol, este tiene mayor resistencia a la fatiga a la flexión y posee también mejores propiedades físicas, propiedades que explican el comportamiento de las propiedades mecánicas. Se nota que los compuestos de matriz polímero son mucho más resistentes que el de matriz cerámica, tanto así, que en algunos casos, estos compuestos de polímeros duplican o triplican el valor del esfuerzo de los demás. Puesto que la resistencia a la fatiga es mayor al disminuir el tamaño de partículas, y al aumentar la plasticidad y resistencia de la sustancia que sirve de aglutinante (Askeland, 2006).
La vida útil de los materiales estudiados se puede reducir cuando se someten a esfuerzos cíclicos y grandes cargas, o al aumentarse la frecuencia. La posible falla que pudieran presentar estos compuestos se debe a sus defectos superficiales, por lo que, hubo baja plasticidad, esencialmente, en el compuesto de matriz cerámica durante acción de la carga aplicada. Finalmente, la resistencia a la fatiga de los compuestos depende de muchos factores, entre los cuales pueden mencionarse: la composición química, el tipo de enlace atómico, el medio ambiente, el tipo y la forma en que se aplica la carga.
3.4 RESULTADOS DEL ANÁLISIS FRACTAL DE LAS SUPERFICIES FRACTURADAS POR FLEXIÓN Y FATIGA
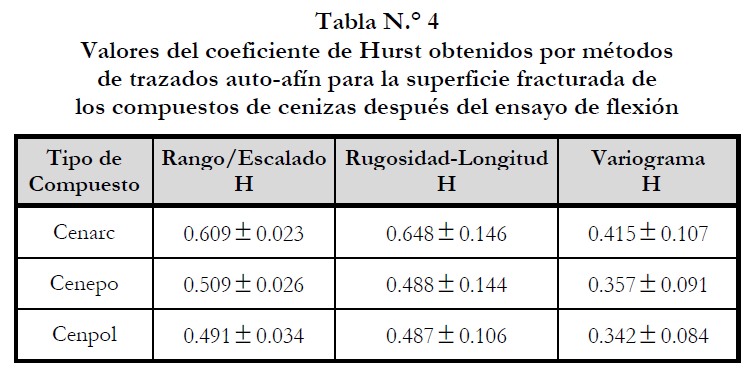
En la tabla N.° 4, se presentan los valores del exponente de Hurst (H) correspondiente al perfil de la zona de fractura de los especímenes de los compuestos estudiados, producido por el esfuerzo de flexión durante el ensayo de resistencia a la flexión.
Al analizar el exponente de Hurst puede explicarse el comportamiento de la resistencia a la flexión de cada compuesto, ya que la rugosidad del perfil de la zona de fractura de estos es análoga a sus módulos de ruptura. Este coeficiente de rugosidad está relacionado con la dimensión fractal de dicho perfil a través de la ecuación 1 (Balankin et al., 1997c) y (Monroy, 2002).
Donde es la dimensión fractal, es el exponente de Hurst y es una constante que viene dada por la fórmula. La dimensión fractal es la dimensión fraccionaria de la periferia de fractura de cada espécimen que estuvo en tensión durante el ensayo de flexión (Soto, 2007). Los perfiles de fractura de los compuestos causados por flexión se muestran en la figura N.° 7.

En la figura N.° 7, pude observarse que algunas de estas superficies resultaron más contraídas que las otras. Las que están más rugosas poseen un valor pequeño de H, tal como es el caso de Cenpol que tiene un menor valor de este exponente, siendo este menor de 0.5 (tabla N.° 4), lo que indica que el valor de H tiende a cero y la dimensión fractal tiende a 2; un plano. Por consiguiente, la zona de fractura de este material es más rugosa que la de los otros. La rugosidad es el resultado de la reacción que tuvieron las partículas para mantenerse vinculadas ante un determinado esfuerzo de flexión que quería romper sus enlaces, y cuando este se incrementó más asperezas aparecieron en el entorno. Por lo tanto, puede decirse que cuando se incremente la resistencia a la flexión en cada uno de estos compuestos, sus correspondientes valores de H disminuirán (tablas 2, 3 y 4).
Sin embargo, Cenepo y Cenarc no presentan muchas asperezas en sus superficies de fractura por lo que sus correspondientes valores de H resultaron ser mayor de 0.5 (tabla N.° 4). Como consecuencia, sus dimensiones fractales tienden a un valor de 1; una línea (Monroy, 2002), (Campos, 2005). Sus perfiles de fractura son lisos y no presentaron una alta reacción a la carga aplicada durante el ensayo, por lo que tienen bajos valores de sus módulos de ruptura, respectivamente, en comparación con los otros compuestos (tablas 2, 3 y 4).
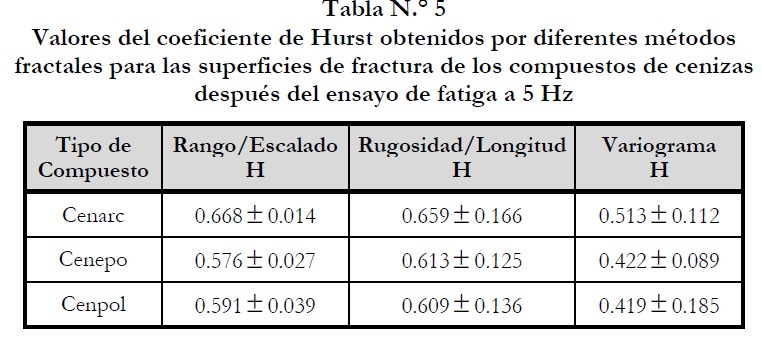
Los resultados del exponente de Hurst del perfil de la zona de fractura de las probetas de estos materiales, causado por un esfuerzo de fatiga a 5 y 10 Hz respectivamente, tal como se ha calculado para otros materiales frágiles (Susarrey, 1999), (Campos, 2005), se presentan en la tabla N.° 5.
La relación que guarda la rugosidad del perfil de la zona de fractura de los compuestos y el coeficiente H determinado a partir de la misma, es igual al análisis que se hizo con los datos de estos parámetros resultantes del ensayo de flexión.
En el estudio fractal de los resultados del ensayo de fatiga a 5 Hz, se tiene que el valor del exponente de Hurst es más grande que el obtenido en el análisis fractal de los resultados por flexión. Esto se puede ver al comparar las tablas 3 y 5, en las cuales se dan los valores de dicho coeficiente obtenidos a través de los métodos de trazado auto-afín que indican en las mismas (Benoit, 1997).
La diferencia que existe entre los resultados de las pruebas, probablemente se deba a que estos compuestos no están aptos para resistir cargas cíclicas, ya que la falla ocurrió después de que debilitaron los materiales por la existencia de poros en sus estructuras, tal como ocurrió en el yeso analizado por Campos y Balankin (Campos, 2005).
La tabla N.° 6 muestra que el valor del exponente de Hurst determinado en el perfil de la superficie fracturada de los materiales causada por un esfuerzo de fatiga a 5 Hz, es mayor que 0.5, por lo que su dimensión fractal tiende a ser la unidad (Soto, 2007). Por lo tanto, las periferias resultantes son lisas y pueden observarse en la figura N.° 8. Al analizar esta propiedad fractal, puede decirse que el compuesto que tiene el coeficiente H más bajo es Cenepo, seguido de Cenpol, y Cenarc, respectivamente.

Los valores de H resultante de la evaluación del perfil de la zona de fractura producido por un esfuerzo de fatiga a 10 Hz, se presentan en la tabla N.° 6, en esta puede observarse que el valor de dicho coeficiente se incrementó con respecto al ensayo de fatiga a 5Hz.
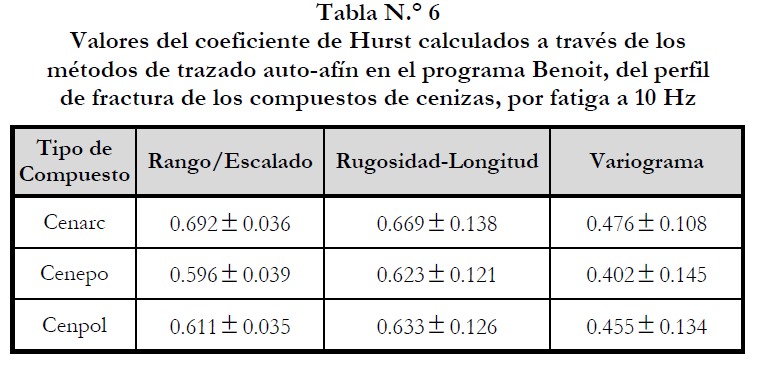
La rugosidad de estos perfiles puede verse en la figura N.° 9, los contornos más arrugados le corresponden un valor de H más grande. Los compuestos mostraron el mismo comportamiento.

El coeficiente H determinado para estos materiales es directamente proporcional a la frecuencia y esta es inversamente proporcional a la resistencia de la fatiga, entonces el esfuerzo a la fatiga es inversamente proporcional a dicho exponente de rugosidad.
3.5 MODELOS PROBABILÍSTICOS
A continuación se presentan los modelos probabilísticos que describen la rugosidad de la zona fracturada producida por flexión. Para dicho fin se obtuvieron los parámetros estadísticos y el tipo de ajuste con la ayuda del programa @Risk (Palisade Corporation 2002) y se sustituyeron en las fórmulas de las funciones de densidad y distribuciones acumuladas correspondiente a la distribución gaussiana inversa en el caso de Cenepo, y normal para el caso de los otros los compuestos (ecuaciones 2-7).
Para Cenarc, se tiene que:
Para Cenepo, se tiene que:
Para Cenpol, se tiene que:
Los modelos de densidad de cada material (ecuaciones 2, 4 y 6) que sirven para analizar la falla producida por la carga aplicada durante el experimento de flexión se muestran en la figura N.° 9. Estas ecuaciones son las áreas bajo las curvas, según se requiere, tienen un valor igual a la unidad (Mendenhal et al., 1997). Se puede ver también que las curvas tienen forma de campana; las cuales son estrechas para los valores pequeños de la desviación estándar correspondiente a cada material y el área de cada curva es grande para los valores grandes del coeficiente de rugosidad, y ensanchadas para los valores grandes de dicha desviación estándar y el área bajo estas curvas es pequeña para valores pequeños del exponente de Hurst contenidos en la tabla N.° 6, que se muestran en la figura N.° 10.
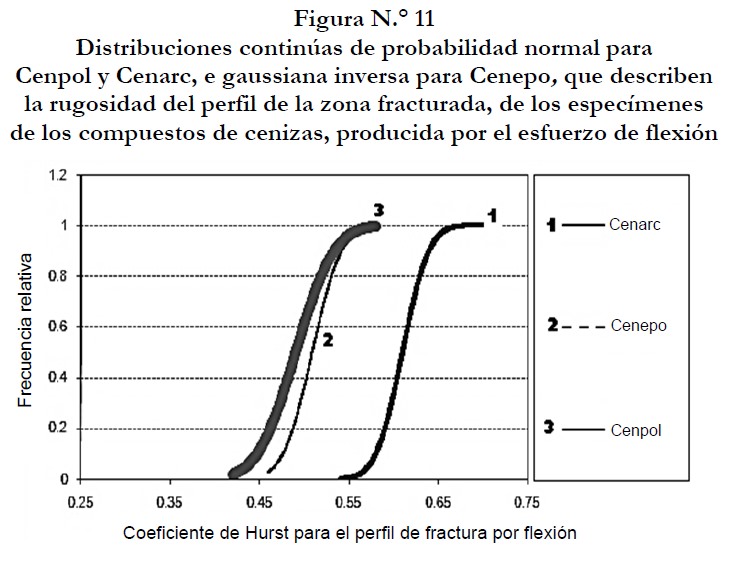
Las curvas tienen diferentes medias y desviaciones estándar; en la figura N.° 10, se observa que están descentralizadas en incomparables posiciones sobre los ejes horizontales y la forma de las curvas refleja el valor de las desviaciones. Asimismo, se tienen las funciones de distribución acumulada normal para los materiales que muestran el comportamiento en la figura N.° 11 y de estas se tienen sus modelos o ecuaciones 3, 5 y 7. Estas curvas sirven para estudiar la rugosidad del perfil de fractura producido por la carga de flexión y en las cuales pueden analizarse e interpretar los puntos de percentil, decil y cuartil para poder hacer afirmaciones acerca del exponente de Hurst y el estado de la superficie de cada compuesto.
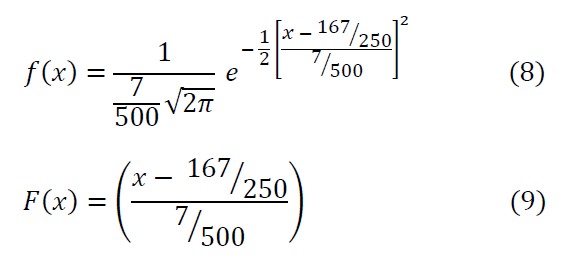
Los modelos de probabilidad que muestran el comportamiento del coeficiente fractal de las periferias de la zona de fracturas de cada uno de los materiales ocasionadas por la carga aplicada a una frecuencia de operación de 5 Hz (tabla N.° 5), se representan a través de las ecuaciones 8-13.
Para Cenarc, se tiene que:
Para Cenepo, se tiene que:
Para Cenpol, se tiene que:
Los modelos probabilísticos que representan las funciones de densidad y de distribución acumulada del comportamiento del coeficiente de Hurst del perfil de las superficies fracturadas de los compuestos, ocasionado por el esfuerzo de fatiga a una frecuencia de 5 Hz, se dan a conocer los modelos de ecuaciones 14-19 para el caso del ensayo realizado a una frecuencia de 10 Hz.
Para Cenarc, se tiene que:
Para Cenepo, se tiene que:
Para Cenpol, se tiene que:
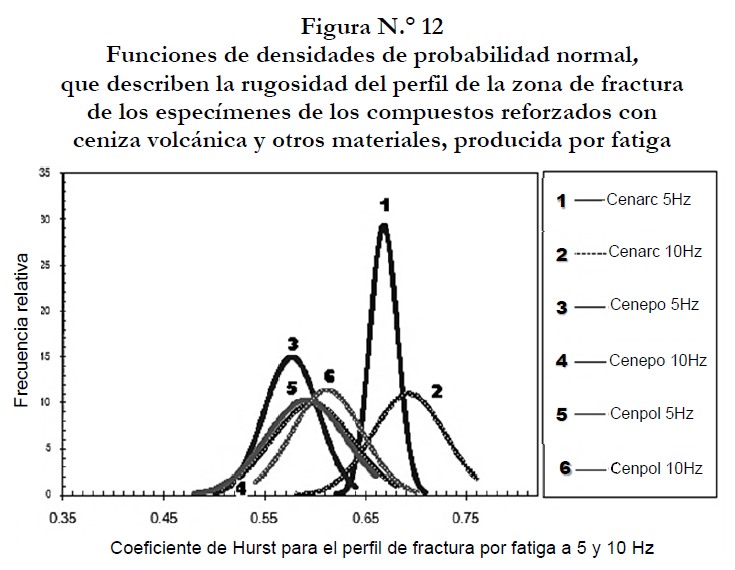
Los modelos probabilísticos que representan el comportamiento fractal del perfil de las superficies fracturadas por fatiga de los compuestos siguen el modelo de una curva de distribución normal, tal como se muestran en las figuras 12 y 13.
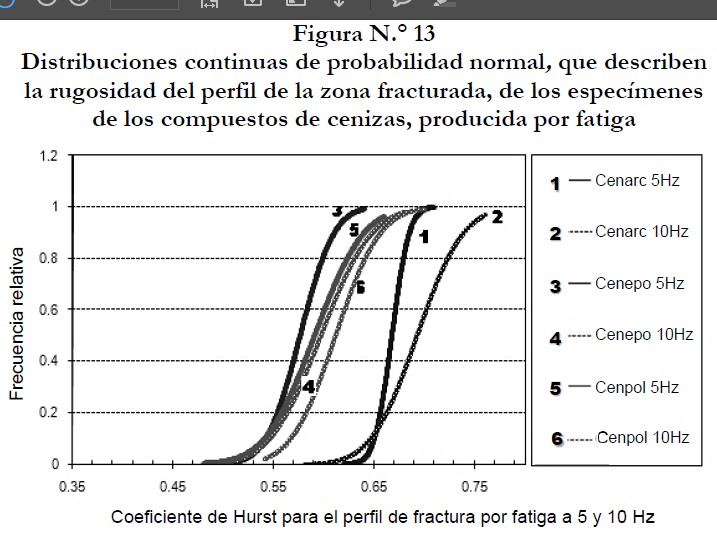
La figura N.° 12 muestra las distribuciones continuas de probabilidad normal, que describen la rugosidad del perfil de la zona fracturada, de los especímenes de los compuestos de cenizas. La curva en forma de campanas depende de la media y de la desviación estándar de la distribución considerada. Estas curvas son estrechas para los valores pequeños de la desviación estándar y el área bajo de cada curva es grande para los valores grandes del coeficiente de Hurst estudiado (tablas 5 y 6) y ensanchadas para los valores grandes de dicha desviación estándar y el área bajo estas curvas es pequeña para valores pequeños de dicho exponente de rugosidad. Además, puede observarse que a mayor frecuencia de operación el área bajo la curva se hace más grande, y normalmente se ensancha debido a la dispersión de los valores del parámetro de escala. Los modelos de las distribuciones acumuladas normales que indican la confiabilidad de los compuestos durante el tiempo que permanecieron bajo los efectos repetitivos de la carga de flexión hasta que fallaron, se muestran en la figura N.° 13.
4. Conclusiones
Cuando se analizan los especímenes de pruebas, puede observarse en ellos que la porosidad guarda una relación directamente proporcional a la dureza; conforme disminuye el volumen de poros de estos compuestos aumenta la dureza de los mismos. En general, la porosidad es perjudicial para las propiedades mecánicas, ya que el tipo de falla mecánica que se presentó en estos compuestos durante los ensayos, se debió a los poros que permanecieron presentes desde los procesos de manufactura. Asimismo, el porcentaje de absorción de agua es una variable muy significativa en estos compuestos debido a que está relacionado con la resistencia a la compresión. Cuanto más bajo es este coeficiente de impregnación, tanto más elevada es dicha resistencia mecánica. Por lo tanto, el material es menos poroso. La existencia de defectos en la microestructura de en estos materiales es una de las razones por las cuales los compuestos mostraron un comportamiento frágil bajo carga durante los ensayos mecánicos realizados. En general, las propiedades físicas y componentes químicos de estos materiales afectan las propiedades de flexión y fatiga de los mismos.
Por otro lado, el valor del exponente de Hurst se relaciona con las microestructuras heterogéneas de los compuestos estudiados, por lo tanto, la propagación de grieta en estos materiales rugosos debido a un esfuerzo de flexión o de fatiga produjo un perfil cuyo coeficiente de rugosidad está comprendido entre 0.513 y 0.668 producido por la carga de fatiga y entre 0.428 y 0.624 ocasionado por la fuerza de deflexión. A partir de este estudio, se deduce que los compuestos que tienen un bajo valor del exponente de rugosidad, tienen mayor resistencia a la flexión y a la fatiga que los que poseen un elevado valor de dicho coeficiente fractal.
El estudio de probabilidad sirvió para determinar los modelos probabilísticos que describen el comportamiento fractal de las secciones fracturadas de los especímenes por flexión y fatiga, y definen la probabilidad de que estos materiales compuestos resistan correctamente bajo condiciones experimentales determinadas.
Las propiedades mecánicas tienen un modelo de distribución normal, lo que explica que el comportamiento mecánico probabilístico de estos compuestos converge en forma adecuada con dicha distribución, la cual es un indicador de la variabilidad de las resistencias analizadas en dichos compuestos debido a una distribución de defectos microestructurales.
5. Reconocimientos
Se agradece el apoyo brindado por el Instituto Nacional de Investigaciones Nucleares de México, Instituto Politécnico Nacional de México D. F. y al Instituto Tecnológico de Santo Domingo (INTEC) por el apoyo brindado para llevar a cabo esta investigación.
6. Referencias bibliográficas
American Society for Testing Materials (1988). ASTM C 373-88. standard test method for water absorption, bulk density, apparent porosity and apparent specific gravity of fired whiteware products. West Conshohocken, Pennsylvania: ASTM. 1-2 pp.
American Society for Testing Materials (1988). ASTM C 674-88. standard test method for flexural properties of ceramic whiteware materials. West Conshohocken, Pennsylvania: ASTM 205208 pp.
American Society for Testing Materials (1996). ASTM C 1360-96. standard practice for constant-amplitude, axial, tension-tension cyclic fatigue of continuous fiber-reinforced ceramics at ambient temperatures. West Conshohocken, Pennsylvania: ASTMA. 1-6 pp.
American Society for Testing Materials (1997). ASTM C 1368-97. standard test method for determination of slow crack growth parameters of advanced ceramics by constant stress-rate flexural testing at ambient temperature. West Conshohocken, Pennsylvania: ASTM. 1-9 pp.
Asaka, T., & Ozeki, K. (1992). Manual de herramienta de calidadEl enfoque japonés. Madrid: Tecnología de Gerencia y Producción.
Askeland, D., & Phulé, P. (2006). The Science and Engineering of the Materials. (5ta. Ed.). México: Thomson Brooks/Cole.
Balankin, A. S. (1996). Models of Self-Affine Cracks in Brittle and Ductile Materials, Philosophical Magazine Letters, 74(6), 415-422.
Balankin, A. S., & Ortega, A. B. (1996). Fractal Concepts for Solid Mechanics, Solid Mechanics and Its Applications, Kluver, Netherlands, 339-343.
Balankin, A. S.; Bravo Ortega, A.; Galicia-Cortes, M. A., & Susarrey, O. (1996). The Effect of Self-Affine Roughness on Crack Mechanics in Elastic Solids, International Journal of Fracture, 79, 63-68.
Balankin, A. S., & Sandoval, F. J. (1997). Self-Affine Properties of Fracture Surfaces, Revista Mexicana de Física, 43(4), 554-591.
Balankin, A. S. (1997). Physics of Fracture and Mechanics of Self-Affine Cracks, Engineering Fracture Mechanics (Special Issue: Statistical Fracture Mechanics), 57(2/3), 135-203.
Balankin, A. S., & Bravo Ortega, A. (1997). Diseño de nuevos y avanzados materiales empleando una nueva teoría de mecánica multifractal del Sólido (Trabajo merecedor del primer lugar del Premio Rómulo Garza, por Investigación y Desarrollo Tecnológico, 1996), Transferencia, 38, 18-29.
Balankin, A. S., & Susarrey, O. (1999). A New Statistical Distribution Function for Self-Affine Crack Roughness Parameters, Philosophical Magazine Letters, 79, 6.
Benoit™. (1997). Fractal Analysis System. [CD-ROM 1.2.]. St. Petersburg, EE. UU.: TruSoft International Inc.
Bilurbina, L., & Liesa, F. (1990). Materiales no metálicos resistentes a la corrosión. (Vol. 40). Barcelona: Marcombo Boixareu, S. A.
Campos Silva, I. E. (2001). Mecánica probabilística de las grietas auto-afines en materiales frágiles (Tesis de doctorado), México, D. F.: SEPI-ESIME-IPN.
Campos, I.; Balankin, A.; Bautista, & O., Ramírez, G. (2005). Self-affine cracks in a brittle porous material. Theoretical and Applied Fracture Mechanics, 44: 187-191.
Cherepanov, G. P.; Balankin, A. S., & Ivanova, V. S. (1995). Fractal Fracture Mechanics, Engineering Fracture Mechanics, 51: 997-1033.
Farrington, R., & Daniels, A. (1997). Physical Chemistry. (6ta. Ed.). New York: John Wiley and Sons.
Gutiérrez Pulido, H., & De la Vara Salazar, R. (2004).Control estadístico de la calidad y seis sigmas. México, D. F.: McGraw Hill.
Heiken, G., Murphy, S., Hackett, A. & Scott, K. (1995). Volcanic Hazards and Energy. Infrastructures. (Dept. of Energy Code EH-33. Office of Risk Analisys and Technology, USA). LA-UR 95-1087, p. 45.
Hsien-Kuang, L.; Nyan-Hwa, T., & Chih-Chen; C. (2000). Compression Strength of Concrete Columns Reinforced by Non-Adhesive Filament Wound Hybrid Composites. Composites: Part A 31(3): 221-233.
Jastrzebski, Z. D. (1979). Naturaleza y propiedades de los materiales para ingeniería. México: Interamericana.
Kenett, R., & Zacks, S. (2000). Estadística industrial moderna-diseño y control de la calidad. México: Internacional Thomson.
Mendenhall, W., Wackerly, D. D., Scheaffer, & Richard, L. (1994). Estadística matemática con aplicaciones. (2da. Ed.). México: Grupo Editorial Iberoamérica.
Monroy Olivares, C. (2002). Curvas fractales. México: Alfaomega.
Ogi, K.; Shinoda, T., & Mizui, M. (2005). Strength in Concrete Reinforced with Recycled CFRP pieces. Composites: Part A 36: 893-902.
Ortiz, R., & Araña, V. (1996). Daños que pueden producir las erupciones. Serie Casa, 5: 37-9.
Palisade Corporation. (2002). @Risk Risk Analysis and Simulation. (CD-ROM. 4.5). New York: Add-In for Microsoft Excel.
Shackelford, J. F. (1995). Ciencia de materiales para ingenieros. (3ra. Ed.) México: Prentice- Hall Hispanoamericana.
Shigley, J. E., & Mischke, C. R. (1990). Diseño en ingeniería mecánica. (4ta. Ed.). México: McGraw-Hill.
Smith, W. F., & Hashemi, J. (2005). Fundamento de la ciencia e ingeniería los de materiales. (4ta. Ed.) México: McGraw-Hill.
Soto Trinidad, J. L. (2007). Estudio mecánico probabilística de materiales compuestos obtenidos a partir de residuos sólidos Mineros. (Tesis de doctorado). México, D. F.: SEPIESIMEIPN.
Susarrey Huerta, O. (1999). Mecánica de grietas auto-afines en un material compuesto. (Tesis de doctorado), México, D. F: SEPI-ESIME-IPN.
Tani, T. (1999). Processing, Microstructure and Properties of In-Situ Reinforced Sic. Matrixcomposites. Composites: Part A 30: 419-42.
Walpole, R., & Myers, R. (1992). Probabilidad y estadística. (4ta. ed.). México: McGraw-Hill.
Datos de filiación
José Luis Soto Trinidad. Es profesor, pleno investigador en el Instituto Tecnológico de Santo Domingo (INTEC) en ingeniería mecánica y realiza investigaciones en las líneas de diseño mecánico, mecánica de la fractura, estudio de materiales y fractales conjuntamente con investigadores del Instituto Politécnico Nacional de México. También imparte docencia como profesor de ingeniería en la UASD. Tiene varias publicaciones en revistas indexadas y ha participado como ponente en varios congresos internacionales sobre ingeniería. En junio de 2000, se graduó de Ingeniero Electromecánico Mención Mecánica por la Universidad Autónoma de Santo Domingo (UASD).
En marzo de 2004, se graduó de maestro en Ciencias en Ingeniería Mecánica-Diseño Mecánico por la Escuela Superior de Ingeniería Mecánica y Eléctrica del Instituto Politécnico Nacional de México DF. En julio de 2007, obtiene su doctorado en Ciencias e Ingeniería Mecánica en la misma institución.
Email: sototjoseluis@yahoo.es
