Ciencia y Sociedad, Vol. 38, No. 3 Julio-Septiembre, 2013: p.497-514, • ISSN: 0378-7680 (impresa) • ISSN: 2613-8751 (en línea) • Sitio web: https://revistas.intec.edu.do/

UNA APLICACIÓN DE LA LÓGICA DIFUSA A LA EVALUACIÓN DEL BALANCE DE RIESGOS DE LA INFLACIÓN Y DEL CRECIMIENTO MACROECONÓMICO

An Application of Fuzzy Logic to the Evaluation of the Risk Balance of Inflation and Growth macroeconomic

DOI: http://dx.doi.org/10.22206/cys.2013.v38i3.pp497-514

Lisette Santana Jiménez

Recibido: 25/04/2013 ● Aprobado: 23/07/2013

Cómo citar: Santana Jiménez, L. (2013). Una aplicación de la lógica difusa a la evaluación del balance de riesgos de la inflación y del crecimiento macroeconómico. Ciencia y Sociedad, 38(3), 497-514. https://doi.org/10.22206/cys.2013.v38i3.pp497-514

Resumen

En este trabajo se aplica una rama de la matemática denominada lógica difusa para la evaluación del balance de riesgos de variables macroeconómicas, utilizando información no numérica, datos históricos y proyecciones correspondientes a las mismas. Los resultados obtenidos por medio del modelo de inferencia difusa resultan coherentes con el sesgo del balance de riesgos determinado en función del criterio de expertos, de la volatilidad asociada a las variables consideradas y los errores cuadráticos medios obtenidos a partir de determinados modelos de proyección, para el período seleccionado.

Palabras clave:

Aplicación, lógica difusa, balance de riesgo, variables macroeconómicas, inflación, crecimiento, modelos de proyección.

Abstract

This paper applies a branch of mathematics called fuzzy logic to evaluate the balance of risks of macroeconomic variables using non-numerical information, historical data and projections for the same. The results obtained through fuzzy inference model are consistent with the bias of the balance of risks determined according to the criteria of experts, the volatility of the variables considered and the mean square errors obtained from certain projection models for the selected period.

Keywords:

Application, fuzzy logic, balance risk, macroeconomic variables, inflation, growth projection models.

i. Introducción

La conducción de la política monetaria bajo el esquema de metas de inflación debe considerar tanto la trayectoria más previsible de las variables económicas como un análisis de los riesgos asociados a escenarios alternativos.

La importancia del análisis de riesgos radica en el hecho de que todo ejercicio de proyección está sujeto a grados de incertidumbre. Por esta razón, resulta importante llevar a cabo una evaluación de los riesgos a los cuales pueden estar sujetas las variables macroeconómicas en función de la posible evolución de los factores que influyen sobre las mismas y que podrían ocasionar desviaciones con respecto a su senda modal.

Actualmente, dicha evaluación está cimentada fundamentalmente en la opinión de los expertos en política monetaria, y constituye un insumo importante en los Informes de Política Monetaria, en los Informes de Proyección Inflacionaria y en la elaboración de los gráficos de abanico (Fan Charts).

Pese a que el juicio de expertos representa un criterio de gran ponderación e importancia al momento de analizar de forma íntegra la coyuntura económica existente y la manera en que la misma puede incidir sobre el comportamiento de las variables consideradas, resulta interesante contar con una metodología que sirva de complemento a este análisis, brindando información adicional para la toma de decisiones.

El objetivo fundamental de este trabajo consiste en la aplicación de una rama de la matemática denominada lógica difusa para la evaluación del balance de riesgos de variables macroeconómicas utilizando información no numérica, datos históricos y proyecciones correspondientes a las mismas. La lógica difusa ha adquirido preponderancia en diversas áreas, incluyendo economía y finanzas, siendo numerosas sus aplicaciones.

Entre estas aplicaciones se destacan numerosos trabajos en el área de optimización de portafolio e incertidumbre financiera; por ejemplo, Deng, X. & Ronjung L. (2010) plantean un modelo de selección de portafolio basado en lógica difusa, a fin de lidiar con las limitaciones que plantea el enfoque probabilístico para caracterizar los mercados financieros. Asimismo, Tsuda, H. & Saito S. (2010) proponen una metodología de optimización que permite a los agentes construir portafolios que reflejen sus propias percepciones acerca de los riesgos, haciendo uso de la teoría de lógica difusa.

Por otra parte, en el área de microeconomía se aborda a menudo el tema de la racionalidad y la toma de decisiones por parte de los consumidores, e. g. Dompere, K. (2010) discute algunos aspectos básicos relacionados con la teoría de decisión en economía, desde una perspectiva difusa; otros trabajos importantes se encuentran en el área de procesos estocásticos, optimización, evaluación de proyectos y programación.

De manera que es evidente que el uso de esta teoría se ha propagado, al punto de que existen revistas científicas dedicadas exclusivamente a aplicaciones de la lógica difusa en diferentes áreas, ya que es de gran utilidad para representar hechos y relaciones imprecisas o conceptos que no tienen límites claros y cuya definición exige elementos que trascienden la teoría clásica de conjuntos.

La estructura de este artículo es la siguiente: en la sección dos se esbozan algunos aspectos básicos relativos a la teoría de lógica difusa y a la construcción de sistemas de inferencia difusa; en la sección tres se realiza un ejercicio simple de inferencia para determinar el balance de riesgos tanto de la inflación como del crecimiento y, finalmente, se presentan las conclusiones del trabajo.

II. Lógica difusa: aspectos generales

En la teoría de probabilidad existen diversas metodologías para lidiar con la incertidumbre. No obstante, existe un tipo de incertidumbre que no es medible o cuya medida debe incorporar tanto valores numéricos como percepciones meramente humanas y que, por tanto, no puede ser tratada haciendo uso de la probabilidad. En otras palabras, cuando se cuenta con información imprecisa, los instrumentos estadísticos resultan insuficientes para obtener resultados significativos. La lógica difusa surge precisamente para tratar de encontrar soluciones óptimas a este tipo de problemas.

Medina & Paniagua (2007) señalan que una de las principales ventajas de la lógica difusa es que permite definir e incluir en un análisis conceptos o variables, aun cuando no estén formulados de forma precisa.

Antes de hacer referencia a la metodología en que se fundamenta la creación de un sistema difuso, es necesario señalar que un conjunto difuso A sobre un conjunto no vacío de objetos X (que se considera como referencial o universo) es un conjunto de pares de valores ${(x, r), x \in X, r \in [0, 1]}$ . Este se caracteriza por una función $μ_{A} : X \to [0, 1]$ , tal que $μ_{A}$ se interpreta como el grado de pertenencia1 a A de cada $x \in X$ . Los valores de pertenencia varían entre 0 y 1, denotando el 0 la no pertenencia y el 1 la pertenencia total.

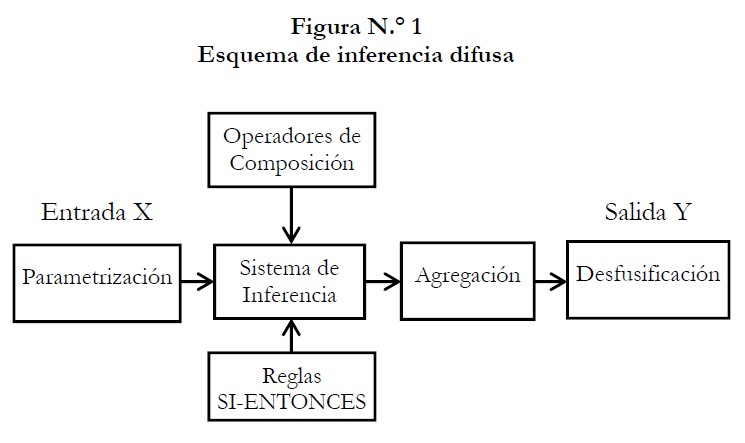
El primer paso para la creación de un sistema difuso es el proceso de parametrización, el cual consiste en definir funciones de pertenencia para cada uno de los valores lingüísticos definidos para las variables de entrada y salida del sistema. Estos valores comúnmente se definen en base a las opiniones de expertos, las cuales se distribuyen a lo largo del universo (o rango posible de valores que puede tomar la variable), así como también a partir de información histórica o proyectada.

La definición exacta de la función de pertenencia depende del concepto a tratar, del contexto al que se refiera y de la aplicación. En general, es preferible la utilización de funciones simples a fin de simplificar cálculos y no perder exactitud. A continuación se enumeran algunas de las funciones de pertenencia típicas:

• Función Triangular
• Función Gamma
• Función S
• Función Gaussiana
• Función Trapezoidal
• Función Pseudo-exponencial
• Función Trapecio extendido

Una vez establecidas las funciones de pertenencia apropiadas, el siguiente paso sería la definición de las implicaciones; es decir, se debe asignar una función de pertenencia a una agrupación antecedente consecuente del tipo $p \to q$ . Las relaciones de implicación son la base del razonamiento basado en reglas y es necesario formalizar el significado de dichas relaciones de causa-efecto. En lógica difusa la metodología más utilizada para este fin es la propuesta por Mamdani (1977):

p \to q \equiv p^{q} \Rightarrow μ_{p \to q} (u, v) = \min (μ_{A} (u), μ_{B} (v))

Donde $u, v$ son universos de discurso y $u \in X, v \in V$ .

Como parte final del proceso, se debe pasar de una respuesta difusa, que se origina a partir del sistema, a una respuesta no difusa. Esta transformación se denomina desfusificación. Existen diversos métodos para lograr dicha transformación y la elección del mismo depende del problema en cuestión.

III. Evaluación del balance de riesgos

La determinación de un balance de riesgos para el comportamiento futuro de variables macroeconómicas tales como la inflación y el crecimiento puede considerarse un problema que atañe a la teoría de conjuntos difusos, ya que se origina tanto del juicio de expertos con respecto a las posibles desviaciones de dichas variables con relación a su comportamiento previsto, como de las proyecciones y la información histórica asociadas a las variables explicativas.

El producto final es un conjunto de valores numéricos (grados de pertenencia), interpretados de manera individual como la posibilidad de que el balance de riesgos de la variable en cuestión esté sesgado al alza, a la baja o que permanezca constante.

La obtención de los conjuntos difusos para fines de este ejercicio se llevó a cabo utilizando el algoritmo de agrupamiento difuso denominado Fuzzy C-Means (Bezdek et al., 1984), el cual consta de los siguientes pasos:

1) Construcción de una matriz de grados de pertenencia, asignando valores arbitrarios para cada observación en cuestión, de tal manera que se cumpla que $\underset{}{\sum μ_{i j}^{}} = 1$ ;

2) Calcular los centroides2 en torno a los cuales se lleva a cabo el agrupamiento de los datos en diferentes conjuntos (clusters), de manera que los objetos ubicados en un determinado conjunto guardan un mayor grado de similitud entre ellos, que con los elementos ubicados en los demás grupos. Para este fin se utiliza la fórmula:

c_{i} = \frac{1}{\sum_{j - 1}^{N} (μ_{i} (x_{j}))^{m}} \sum_{j - 1}^{n} (μ_{i} (x_{j}))^{m} x_{J} i = 1, . . ., c

3) Recalcular, usando expresión del paso 2, una nueva matriz de grados de pertenencia usando los centroides obtenidos en el paso anterior:

μ_{i} (x_{j}) = \frac{(\frac{1}{∥ x_{j} - c_{i} ∥^{2}})^{\frac{1}{(m - 1)}}}{\sum_{i = 1}^{C} {(\frac{1}{∥ x_{j} - c_{i} ∥^{2}})}^{\frac{1}{(m - 1)}}} i = 1, . . ., c j = 1, . . ., n

Los pasos dos y tres se repiten hasta que el valor de la función:

j_{m =} \sum_{i - 1}^{2} \sum_{j - 1}^{n} [μ_{i} (x_{j})]^{m} ∥ x_{j} - c_{i} ∥_{A}^{2} 1 \leq m < \infty

Se minimiza; dicha minimización se logra cuando:

m a x_{i j} \{|μ_{i j}^{(k + 1)} - μ_{i j}^{(k)}|\} < ε, donde ε \in [0, 1]

En la función objetivo $J_{m}$ las variables son las siguientes:

$X = {x_{1}, x_{2}, . . . x_{n}} \subset R^{n}$ , datos;

$n$ = número de agrupamientos (clusters) en $X$ , tal que 1 < c < n;

$m$ = exponente de ponderación, tal que 1≤ m < ∞;

µ = grado de pertenencia de cada observación de $X$ ;

$c_{i}$ = vector de centroides;

BALANCE DE RIESGOS DE LA INFLACIÓN

Las variables consideradas para determinar el balance de riesgos de la inflación3 fueron las desviaciones estándar históricas correspondientes a las variables siguientes: crecimiento de Estados Unidos $(^{σ} c r e c_E U A)$ , inflación de Estados Unidos $(^{σ} π_U S A)$ y el EMBI $(^{σ} E M B I)$ , a fin de recoger la volatilidad histórica de dichas variables, así como también un Indicador de Impulso Fiscal⁴ (IIF), con la finalidad de considerar el efecto de posibles desviaciones en la política fiscal sobre la trayectoria inflacionaria. Asimismo, es importante acotar que como variable independiente no se utilizó la inflación per-se, sino una serie de los errores cuadráticos medios (ECM) obtenidos a partir de la batería de modelos de proyección.

Para cada una de estas variables se construyeron tres conjuntos difusos denominados “Alto”, “Bajo” y “Constante”, haciendo alusión al sesgo del balance de riesgos en cada caso y, en el caso del IIF los conjuntos difusos se refieren a la orientación de la política fiscal; es decir, si fue contractiva, neutral o expansiva. Como se señala anteriormente, el agrupamiento de las observaciones en sus respectivos conjuntos difusos se llevó a cabo usando el algoritmo Fuzzy C-Means. Los resultados del agrupamiento se presentan en la figura N.° 2.

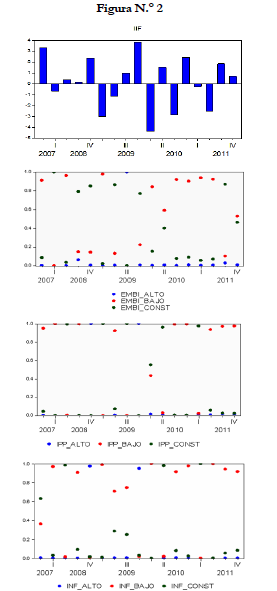
La figura muestra el agrupamiento de cada variable explicativa en los diferentes conjuntos difusos con sus respectivos grados de pertenencia. En el caso del IIF no se llevó a cabo un agrupamiento con el algoritmo Fuzzy C-Means; para las demás variables que se presentan en la figura N.° 2, los puntos de colores indican lo siguiente:

• Azul = valor del grado de pertenencia de la variable al conjunto difuso denominado “Alto”;

• Rojo = valor del grado de pertenencia al conjunto “Bajo”;

• Verde = valor del grado de pertenencia al conjunto difuso “Constante”.

Un problema en lógica difusa se caracteriza por una función de pertenencia que varía en función de la aplicación en cuestión. En este caso, tras catalogar cada observación en los conjuntos difusos definidos, se determinó que el mejor ajuste se corresponde, en cada caso, con funciones de pertenencia de tipo triangular.5

Una vez realizada esta caracterización, se inició el proceso de inferencia difusa, aplicando reglas de tipo SI-ENTONCES, donde el antecedente es la variable explicativa, a fin de determinar cómo se afecta la variable dependiente, que es el consecuente.

Las reglas de inferencia se plantearon de acuerdo con las correlaciones históricas, así como también en función de las relaciones teóricas entre las variables.

Para las diferentes reglas de inferencia formuladas, se utilizó como antecedente (premisa) la conjunción de las variables explicativas y como consecuente (consecuencia) el ECM de los modelos de proyección inflacionaria. Se llevó a cabo un ejercicio sobre la muestra (para el año 2011, con periodicidad trimestral) a fin de determinar si los resultados de las reglas de inferencia son coherentes con los valores observados del ECM para cada período; así como también para verificar si los mismos coincidieron con la opinión de los expertos con respecto al sesgo del balance de riesgos. Los resultados se muestran en la figura N.° 3.

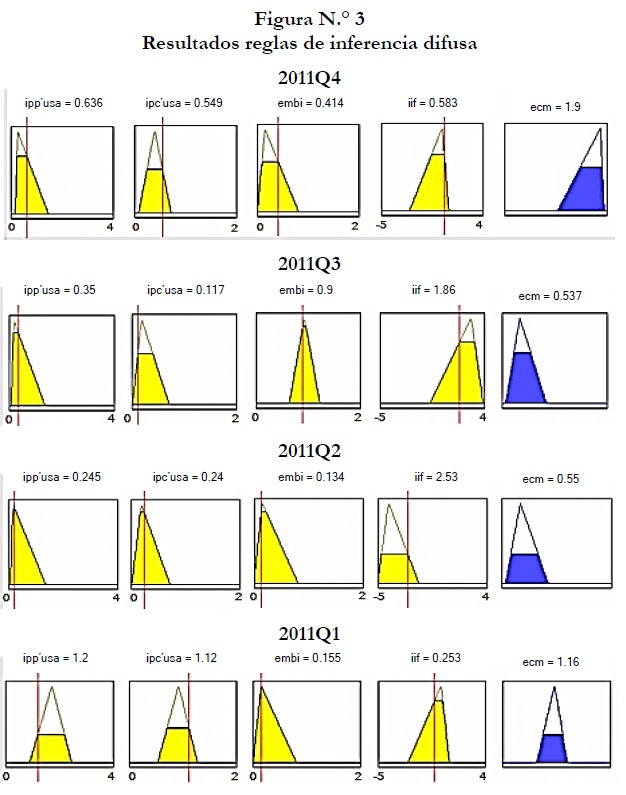
La interpretación de las figura N.° 3 es sencilla; en cada panel, los gráficos de color amarillo representan el antecedente de la proposición, donde el nivel que alcanza el interior de la función de pertenencia (en este caso de tipo triangular) denota el grado de pertenencia de cada variable a un determinado conjunto difuso, mientras que los gráficos de color azul representan los respectivos consecuentes, cuyo grado de pertenencia a un conjunto difuso se infiere a partir de los supuestos que conforman el antecedente. Por ejemplo, si tomamos el segundo trimestre del año 2011 vemos, que dados los supuestos, los cuales pertenecen al conjunto difuso denominado “Bajo”, con altos grados de pertenencia (salvo el IIF), por medio de la regla de inferencia se determina que el consecuente (en este caso el ECM) pertenece igualmente al conjunto difuso “Bajo” con un grado de pertenencia de 0.5.

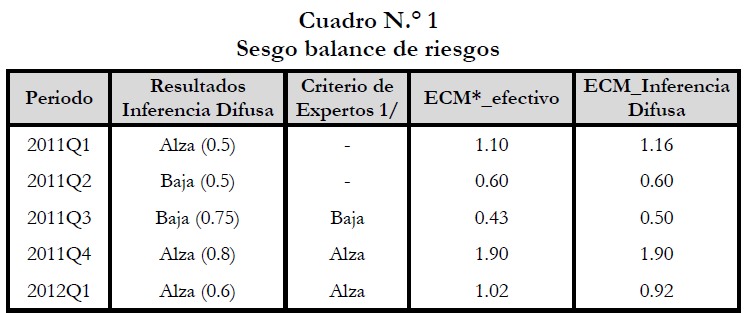
El cuadro 1 resume los resultados, mostrando las comparaciones que se realizan con el ECM efectivo y el sesgo del balance de riesgos de acuerdo al criterio de expertos, mostrándose coincidencia entre dicho criterio y el sesgo del balance de riesgos resultante del modelo de inferencia difusa. Asimismo, se observa que los errores cuadráticos que se obtienen a partir de las reglas de inferencia son iguales o muy cercanos a los observados.

BALANCE DE RIESGOS DEL CRECIMIENTO

El ejercicio realizado para evaluar el balance de riesgos de la inflación puede ser efectuado para el caso del crecimiento, siendo en este caso las variables explicativas la desviación estándar de la depreciación $(^{σ} D e p)$ y del crecimiento de Estados Unidos $(^{σ} c r e c_U S A)$ , en tanto que la variable dependiente es la desviación estándar del crecimiento ⁶ $(^{σ} c r e c_R D)$

Análogamente, el algoritmo empleado para agrupar los conjuntos difusos es el Fuzzy C-Means (figura N.° 4) y los conjuntos difusos en cuestión (“Alto”, “Bajo”, “Constante”) fueron caracterizados con funciones de pertenencia de tipo triangular.

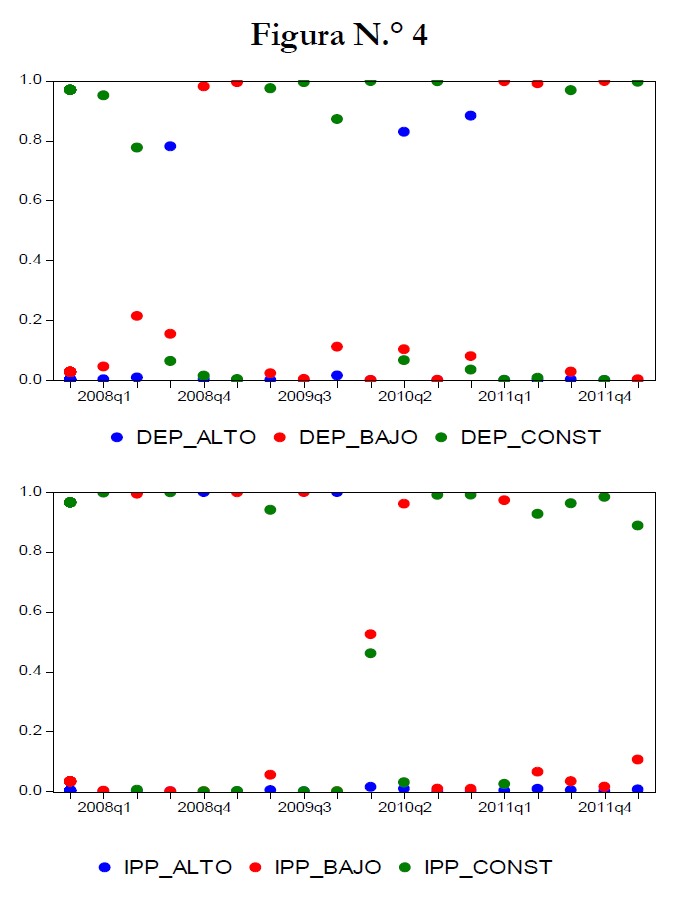
La figura muestra el agrupamiento de cada variable explicativa en los diferentes conjuntos difusos con sus respectivos grados de pertenencia. Los puntos de colores indican lo siguiente:

• Azul = valor del grado de pertenencia de la variable al conjunto difuso denominado “Alto”;

• Rojo = valor del grado de pertenencia al conjunto “Bajo”;

• Verde = valor del grado de pertenencia al conjunto difuso “Constante”.

Los resultados de las reglas de inferencia difusa con sus respectivos grados de pertenencia al conjunto difuso para el período en cuestión se observan en el cuadro N.° 2.

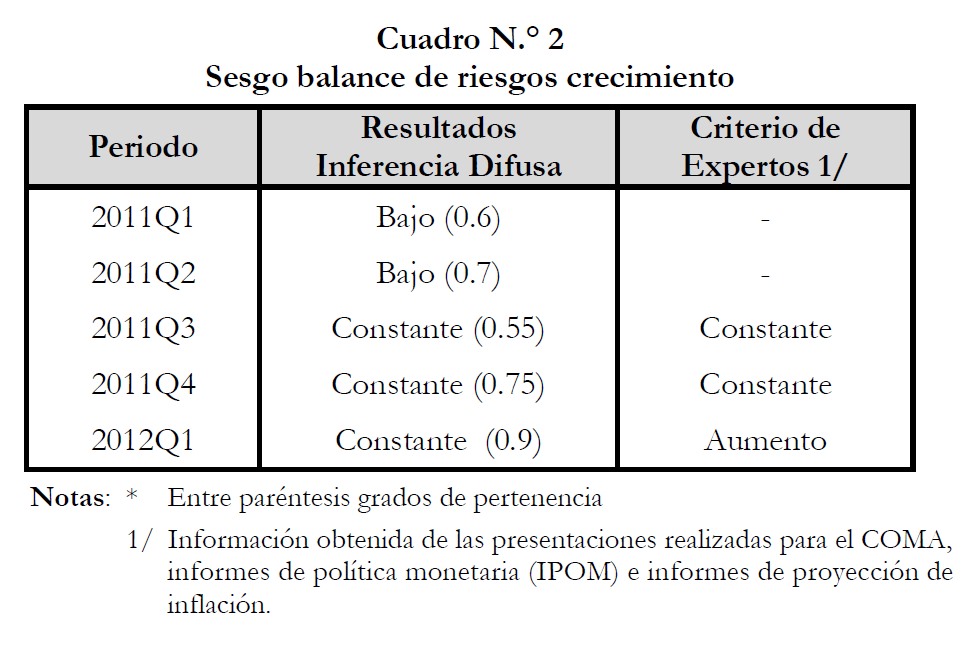
En este caso, el sesgo del balance de riesgos que se obtiene a partir del modelo de lógica difusa exhibe coherencia con el criterio de expertos para los trimestres considerados, salvo para el primer trimestre del 2012; no obstante, esta divergencia puede ser producto de que este criterio se basa en las posibles desviaciones de la brecha del producto, mientras que el modelo considera exclusivamente la incertidumbre asociada al crecimiento per-se.

IV. Conclusiones

La evaluación del balance de riesgos en regímenes con metas de inflación resulta de gran importancia, ya que así como resulta necesario contar con modelos que permitan proyectar la trayectoria de las variables macroeconómicas de interés, es inminente incorporar en dicho análisis una apreciación de la incertidumbre a la cual está sujeta dicha proyección.

En este sentido, resulta de interés contar con una metodología que complemente el criterio de los expertos en política monetaria o mejor aún, una herramienta que permita incorporar dicho criterio con miras a obtener resultados más precisos.

En este caso, el uso de un modelo de inferencia difusa puede ser útil por diversas razones, incluyendo el hecho de que generalmente no se cuenta con la información suficiente para aplicar modelos matemáticos convencionales, por lo que la implementación de modelos alternativos que tomen en cuenta estas limitaciones y que a la vez permitan incorporar conceptos relativos a la realidad constituye una opción interesante.

La agenda de trabajo a desarrollar en torno a este modelo incluiría la eventual incorporación de nuevas variables explicativas (en caso de ser necesario), así como también la calibración de las reglas de inferencia de acuerdo a la opinión de los expertos en política monetaria, a fin de plantear los escenarios posibles con sus respectivas posibilidades de ocurrencia (grados de pertenencia) y lograr resultados cada vez más precisos que ayuden a la toma de decisiones.

Referencias bibliográficas

Aparecido, R., & Moura, R. (2011). Fuzzy logic and behavioral finance: A connection. Economics and Financial Research, 4, 450-454.

Bezdek, J., Ehrlich, R., Full, W. (1984). The Fuzzy C-Means Clustering Algorithm. Computers and Geosciences, 10(2-3), 191-203.

Bojadziev, G., & Bojadziev, M. (1997). Fuzzy Logic for Business, Finance and Management. (2da. Ed.). New Jersey: World Scientific Publishing, Co., Inc.

Deng, X., & Rongjun, L. (2010). A portfolio selection model based on possibility theory using fuzzy two-stage algorithm. Journal of Convergence Information Technology 5 (6), 138-145.

Dompere, K. (2010). Fuzziness, Rationality, Optimality and Equilibrium in Decision and Economic Theories. Studies in Fuzziness and Soft Computing, 254, 3-32.

Klir, G., & Yuan, B. (1995). Fuzzy Sets and Fuzzy Logic: Theory and Applications. New Jersey: Prentice-Hall.

Mamdani, E. (1977). Application of Fuzzy Logic to approximate reasoning using linguistic synthesis. IEEE Transactions on Computers, 26, 1182-1191.

Medina, S., & Paniagua, G. (2007). Modelo de inferencia Difuso para Estudio del Crédito. Dyna, 154, 215-229.

Tsuda, H., & Saito S. (2010). Application of Fuzzy Theory to the Investment Decision Process. Studies in Fuzziness and Soft Computing, 254, 365-387.

Wittman, T. (2002). Time Series Clustering and Association Analysis of Financial Data. CS 8980 Project. Recuperado de http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.111.4989&rep=rep1&type=pdf

Datos de filiación

Lisette Josefina Santana Jiménez. Es egresada de la licenciatura de Economía de la Pontificia Universidad Católica Madre y Maestra de Santo Domingo (PUCMM) y maestría de Matemática Pura en el Instituto Tecnológico de Santo Domingo (INTEC). Ha trabajado en el Banco Central de la República Dominicana durante los últimos seis años, donde se ha desempeñado en las áreas de Política Fiscal y, actualmente, trabaja en la División de Modelos Macroeconómicos del Departamento de Programación Monetaria e Investigación Económica. Ha participado en diversos seminarios y conferencias nacionales e internacionales sobre Política Monetaria, Modelación Macroeconómica y Política Fiscal y ha fungido como expositora de los resultados de sus investigaciones en el marco de diferentes seminarios científicos. Ha publicado sus investigaciones en los campos de Economía y Finanzas en revistas especializadas nacionales e internacionales.

Email: lj.santana@bancentral.gov.do