2. INTRODUCCIÓN
Los bancos y sus actividades, generalmente están sujetos a una supervisión oficial mucho más estrecha que otras clases de negocios; ¿qué hay en sus funciones y en su naturaleza que justifica lo anterior? La justificación primaria de la supervisión bancaria es que limita el riesgo de pérdida para los depositantes, y con ello mantiene la confianza del público en los bancos. Si bien la supervisión se enfoca en el banco individual, los supervisores deben estar también alerta acerca de la posibilidad de que los problemas en una institución tengan repercusiones más amplias, sistémicas en otras, o en la integridad del sistema de pagos.
Los supervisores deben estar alerta ante todas esas posibilidades. Aveces las preocupaciones existentes pueden juzgarse como suficientes para promover algún tipo de apoyo oficial al sistema bancario. Aunque tal decisión corresponde al banco central y al gobierno, el detallado conocimiento institucional de los supervisores en esas circunstancias sería de un valor inestimable.
Aunque los supervisores necesitan cierta comprensión de los mercados y del ambiente de negocios en que los bancos operan, no pueden esperar saber tanto como los propios banqueros acerca de las realidades comerciales de la banca. De cualquier modo, no corresponde al papel de los supervisores tomar las decisiones comerciales que son la prerrogativa de la administración de los bancos. Más bien, el supervisor monitorea y evalúa las estrategias, políticas y desempeño globales del banco (donde resulta apropiado con referencia a criterios legales o prudenciales específicos) y llega a una conclusión en cuanto a la solidez del banco y la competencia de los que lo dirigen.
En la búsqueda de mejores métodos para el diagnóstico de la salud financiera de los bancos, se han ensayado muchas opciones, y en la literatura especializada en el tema podemos encontrar evidencias de las bondades de los diferentes métodos. La regresión logística se ha empleado en muchos estudios empíricos para pronosticar insolvencia, véase el trabajo de Huang et al. (2004).
Este trabajo está centrado en el uso de la regresión logística para el diagnóstico de instituciones financieras. Haciendo un recorrido en la literatura especializada publicada hasta la fecha, se pueden resaltar los trabajos de Agresti (2002), sobre el análisis de datos categóricos y su énfasis en los modelos loglineales. También presenta tratamientos muy útiles del modelo logit. Fienberg (1980). Otros como Aldrich y Nelson (1984), muestran una breve introducción a los modelos de regresión para datos dicotómicos. Por otro lado, Collet (2003) hace un tratamiento extensivo de los modelos de regresión para datos binarios y binomiales, con una buena discusión de casos de diagnóstico. Cox y Snell (1989) hacen un recuento elegante del uso de la regresión logística, aunque se trata el tema con un nivel que pudiera presentar cierta dificultad.
En Hinkley et al (1991) esta el mejor tratado resumido sobre modelos lineales generalizados, se describen aplicaciones de diagnóstico y métodos de cuasi- verosimilitud. Por su parte Fox (1997), en el capítulo 15, provee mucho material de estudio sobre modelos lineales y respuestas categóricas. Long (1997) incluye un tratamiento detallado de modelos de regresión dicotómica y politómica, así como también de datos categóricos ordenados.
En relación a la aplicación que se presenta, hay que tener en cuenta que la Superintendencia de Bancos de la República Dominicana, tiene a su cargo la supervisión de 141 instituciones de intermediación financiera, y 112 de intermediación cambiaria. En la actualidad el número de ambos tipos de instituciones tiende a reducirse, debido a las nuevas medidas regulatorias, que han puesto barreras para la entrada de nuevas instituciones al mercado, y a las exigencias de capital para las ya instaladas, lo cual fomenta la fusión de las mismas.
Debido a que la cantidad de instituciones a supervisar abruma la capacidad de los técnicos de la Superintendencia para poder hacer un análisis profundo de las cifras contables reportadas, de todas las entidades, en algunos casos diariamente, sería de gran utilidad contar con una herramienta que hiciera el diagnóstico preliminar de los estados financieros, levantando una señal de alerta cuando se requiera que se haga un estudio más profundo de cada caso. Esto ayudaría a focalizar la atención de los analistas en aquellas instituciones que presentan señales de deterioro, con el objetivo de tomar medidas de prevención con suficiente tiempo de anticipación. Este es el enfoque medular de la supervisión basada en riesgo.
Afortunadamente, la Superintendencia cuenta con un efectivo y eficiente medio de recepción de la información que llega de las instituciones supervisadas. Mensualmente se reciben las cifras contables a través del Estado de Contabilidad Analítico, en forma electrónica. Este estado también se recibe diariamente de parte de los Bancos Comerciales.
Dado que los Bancos Comerciales manejan más del 80% del volumen de activos netos del sector financiero, a ellos se dedica la mayor atención por parte de los analistas de la Superintendencia de Bancos. Las demás instituciones se analizan sobre la base de una supervisión enfocada en riesgo, por lo qué, el análisis de los estados financieros de esas instituciones se relega a un segundo plano.
3. METODOLOGÍA DE LA INVESTIGACIÓN
Como ya se ha dicho en la introducción, la Superintendencia de Bancos de la República Dominicana recibe diariamente las informaciones financieras de las instituciones que supervisa. En base a esas informaciones, la institución evalúa y determina la viabilidad financiera de cada unas de las entidades supervisadas. Dado que el volumen de información es grande, el tiempo necesario para la evaluación de las entidades se hace escaso.
Los métodos de diagnóstico son variados y todos usan como información primaria la que es reportada en los llamados “Estados de ContabilidadAnalíticos”. Estos informes contables tienen el desglose de los resultados de las operaciones del negocio bancario. En base a esta información se construyen indicadores de estructura y financieros que ayudan al analista a hacerse una idea de que tan bien está operando la entidad financiera.
A pesar de que la construcción de los indicadores se hace de forma automatizada, el diagnóstico de la entidad evaluada depende del juicio del analista y del tiempo que este pueda dedicar al análisis de los mismos. Dado el número de entidades a evaluar y que el diagnóstico no oportuno es de reducido valor, se requiere de una herramienta que pueda hacer el diagnóstico tan pronto como llega la información, y que de preferencia, pueda hacer recomendaciones al analista, para este a su vez hacer estudios más profundos.
Para evaluar la pertinencia del uso de los modelos de regresión logística se hará una exposición de los requisitos de aplicación de los mismos, los criterios de evaluación de la bondad de los modelos y de aplicaciones de estos a problemas similares.
Se hará acopio de las cifras de instituciones que se han desempeñado favorablemente en el período que va de noviembre 2002 a enero 2005, y así mismo de las que han tenido problemas en el mismo período.
En el período que va de febrero a diciembre 2005, se verificará que tan efectivos han sido los modelos desarrollados para detectar la posibilidad de anomalías en las entidades de intermediación financiera. Como ya estas cifras son información histórica, los resultados de la prueba serán muy reveladores.
4. RECOMENDACIONES DEL COMITÉ DE BASILEA
Las debilidades en el sistema bancario de un país, desarrollado o en desarrollo, pueden amenazar la estabilidad financiera en ese país y en el exterior. La necesidad de aumentar la fortaleza de los sistemas financieros ha atraído un interés mundial creciente. El Comunicado emitido en la clausura de la Cumbre del G-7, en Lyon en junio de 1996, lanzó un llamado en este sentido. Varios organismos oficiales, incluyendo el Comité de Basilea para la Supervisión Bancaria, el Banco de Pagos Internacionales, el Fondo Monetario Internacional y el Banco Mundial, han examinado recientemente maneras para fortalecer la estabilidad financiera en todo el mundo1.
El Comité de Basilea para la Supervisión Bancaria ha estado trabajando en esta área por muchos años, directamente y mediante sus contactos con los supervisores bancarios en todas partes del mundo. En el último año y medio ha estado examinando la mejor manera de expandir sus esfuerzos dirigidos a fortalecer la supervisión prudencial en todos los países, mejorando sus relaciones con los países ajenos al G-10 así como su trabajo previo para mejorar la supervisión prudencial en sus países miembros. Todo esto en aras de contar con los mecanismos apropiados para fortalecer el negocio de intermediación financiera.
4.1 SISTEMAS DE ALERTA TEMPRANA
La investigación en el desarrollo de sistemas de alerta temprana, para el diagnóstico de instituciones financieras, ha sido de gran interés en los últimos años, tanto por los organismos multilaterales, como el Fondo Monetario Internacional (FMI), como por las agencias locales de cada país a cargo de la supervisión del sistema financiero.
Los sistemas de alerta temprana juegan un papel importante en la evaluación de vulnerabilidades relativas a análisis más detallados para un país específico. Para que un modelo sea efectivo debe probar su adecuación en la evaluación en tiempo real de las cifras de las entidades financieras.
Un resultado típico de los estudios sobre modelos de alerta tempana2 es que producen pronósticos informativos, comparados con el método de adivinar, pero son de dudosa ayuda para un observador bien informado. Esto indica que inevitablemente es mejor un pronóstico basado en amplia información cualitativa y cuantitativa, que el producido por un simple modelo matemático.
Las técnicas automatizadas para el diagnostico de entidades financieras son variadas y cada una de ellas con sus méritos propios. Trippi y Turban (1996) presentan un recuento de las técnicas mas usadas y una evaluación del alcance de las mismas en este campo.
La metodología de CAMEL sirve para calcular indicadores que orientan a una persona de cierta preparación y destreza en el diagnostico de la entidad financiera. Además de esto, ya Salchenberger, Cinar y Lash (1992) hicieron un estudio comparativo de la metodología CAMEL en un sistema automatizado de evaluación financiera con resultados muy variados.
CAMEL viene de las siglas en ingles Capital, Asset, Management, Earnings y Liquidity. Estos son los indicadores usados por la FDIC (Federal Deposit Insurance Corporation) de los Estados Unidos para evaluar la salud de instituciones financieras.
4.2 MODELO DE SUPERVISIÓN DOMINICANO
La Supervisión que realiza la Superintendencia de bancos de la República Dominicana pretende conocer no sólo la situación actual de la entidad financiera, sino su viabilidad en el mediano plazo. Es decir, es una supervisión orientada a determinar no sólo si el balance refleja adecuadamente la situación de la entidad, sino algo igualmente importante, a saber: si la calidad de su gerencia, su posicionamiento actual y futuro, y sus políticas de crédito, de captación de recursos, de servicios, de empleo de remuneraciones, de distribución geográfica, de diversificación de riesgos, etcétera, permiten prever que en el futuro será viable o no.
Para ello la Superintendencia utiliza un método de supervisión similar al aplicado por la OCC (Office of the Comptroller of the Currency) y la Reserva Federal de los Estados Unidos, denominado sistema de calificación CAMELS, el cual ordena la tarea del organismo supervisor dividiendo las áreas de estudio de la entidad financiera en seis componentes3. Los componentes son: Capital, Activos, Management (Administración), Earnings (Rentabilidad), Liquidez y Sensibilidad.
Del mismo modo el manual de supervisión expresa que el método de evaluación y calificación CAMELS constituye un enfoque integrador en el cual las fortalezas y debilidades resultan de un análisis conjunto de los factores claves de riesgo. Por otra parte, el resultado de las inspecciones permite determinar las debilidades del banco en distintas áreas, y focaliza los aspectos sobre los cuales la Gerencia del banco debe concentrar sus acciones correctivas. La entidad financiera recibe una calificación independiente para cada uno de los componentes y una calificación general basada en la evaluación efectuada en relación al grado de cumplimiento de las normas y de la adecuación de los criterios y principios financieros aplicados. La calificación final de la entidad financiera no surge de un promedio aritmético, sino de la consideración general de la situación de la entidad con especial énfasis en el componente “Management” y cualquier otro factor que pueda considerarse de importancia para su desempeño futuro.
5. EL SISTEMA FINANCIERO Y LA ECONOMÍA DOMINICANA
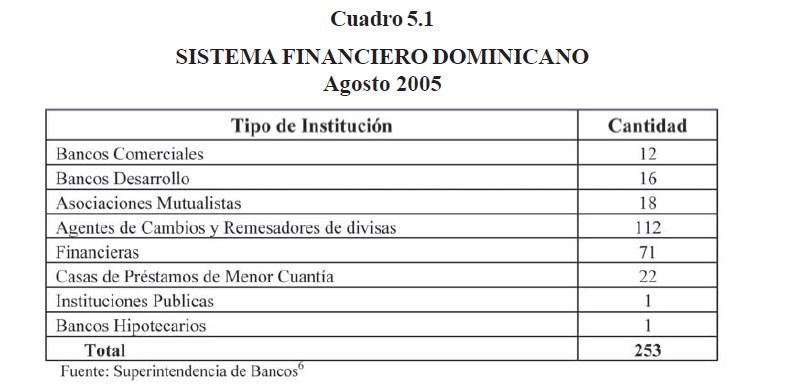
La Superintendencia de Bancos de la República Dominicana, tiene a su cargo la supervisión de 141 instituciones de intermediación financiera, y 112 de intermediación cambiaria, en el cuadro 5.1 se puede apreciar la composición del sistema financiero dominicano en Agosto del 2005. En la actualidad el número de ambos tipos de instituciones tiende a reducirse, debido a las nuevas medidas regulatorias, que han puesto barreras para la entrada de nuevas instituciones al mercado, y a las exigencias de capital para las ya instaladas, lo cual fomenta la fusión de las mismas.
6. INTRODUCCIÓN A LOS MODELOS DE REGRESIÓN LOGÍSTICA
El problema de discriminación o clasificación cuando conocemos los parámetros de las distribuciones admite una solución general. Sin embargo, en la mayoría de las aplicaciones los parámetros son desconocidos y deben estimarse a partir de los datos. Dado que frecuentemente los datos disponibles no siguen distribución normal, y en muchos problemas la variable de respuesta es discreta, se necesita un método especial que pueda salvar estas barreras.
Es debido a las causas antes expuestas, que los modelos de regresión lineal presentan grandes dificultades para atacar problemas con variables de respuesta discreta, Peña (2002)4. Existen otros métodos de reciente creación para atacar el problema de clasificación, algunos de ellos todavía pendientes de evaluación. Por ejemplo el método propuesto por Vapnik y Chapelle (2000), constituye una alternativa el uso de redes neuronales5 para aproximar funciones generales.
Al comparar la regresión logística con otros métodos de clasificación como el análisis discriminante, se nota que la primera parte de unos supuestos menos restrictivos y permite introducir como independientes en el modelo, a variables categóricas6.
Los modelos de regresión, según Hosmer y Lemeshow (2000)7, se han convertido en un componente integral de cualquier análisis de datos que involucre la descripción de la relación entre una variable de respuesta y una o más variables explicativas. Por lo general el modelo de regresión implica una relación lineal entre las variables del mismo, y en esa situación, se dice que el modelo es de regresión lineal. En otros casos, la variable de respuesta es discreta, es decir toma 2 o más posibles valores. Lo que distingue la regresión logística de los modelos de regresión lineal, es fundamentalmente, que la variable de respuesta es dicotómica o binaria, es decir, toma uno de dos valores posibles. Esta diferencia entre ambos modelos, se refleja tanto en la selección de los parámetros del modelo, como en los supuestos para su construcción.
Muchas distribuciones de probabilidad han sido propuestas para el análisis de variables de respuesta dicotómicas. Cox y Snell (1989) discuten algunas de ellas. Ellos recomiendan la distribución logística, por dos razones, primero, desde un punto de vista matemático, es extremadamente flexible y fácil de usar, y segundo, se llegan a conclusiones fácilmente interpretables.
Para simplificar la notación, se usará la cantidad , para representar la media condicional de Y dado x, cuando se use la distribución logística. La forma específica del modelo de regresión logística es:
Una transformación de que es importante en el estudio de la regresión logística, es la transformación logit. Esta transformación se define en términos de, como:
Lo importante de esta transformación es que la función logit,, es lineal en sus parámetros, puede ser continua, y puede estar en el rango de , dependiendo del rango de .
La segunda diferencia importante entre los modelos de regresión lineal y de regresión logística, se refiere a la distribución condicional de la variable de respuesta. En el modelo de regresión lineal se asume que una observación de la variable de respuesta se puede expresar como . La cantidad e es el error, y expresa la diferencia entre la observación y la media condicional. El supuesto más común es que sigue una distribución normal con media y varianza constante en cualquier nivel de la variable independiente. Esto implica que la distribución condicional de la variable respuesta, dado , se distribuirá normalmente con media y una varianza constante. Este no es el caso con una variable dicotómica. En esta situación, se puede expresar el valor de la variable de respuesta dado , como . Donde la cantidad puede asumir uno de dos valores posibles. Si entonces con probabilidad , y si, entonces con probabilidad . Por lo tanto , tiene una distribución con media 0 y varianza igual a Esto quiere decir que la distribución condicional de la variable de respuesta sigue una distribución binomial con probabilidad dada por la media condicional, .
En resumen, se puede decir, que en análisis de regresión, cuando la variable de respuesta es binaria, se cumplen las siguientes premisas:
a) La media condicional de la ecuación de regresión debe ser formulada para estar contenida entre 0 y 1.
b) La distribución binomial y no la normal, describe la distribución de los errores y será la distribución en la que estará sustentado el análisis.
c) Los principios que guían un análisis de regresión lineal, son los mismos para el análisis de regresión logística.
Para aplicar el método, primero se debe construir la función de verosimilitud. Esa función expresa la probabilidad de los datos observados como una función de los parámetros desconocidos. Los estimadores de máxima verosimilitud de esos parámetros son seleccionados de tal forma que maximicen la función. Por lo tanto, los parámetros estimados son los que acercan más la función a los valores observados.
A continuación se muestra como encontrar esos estimadores en el modelo de regresión logística. Si es codificada como 0 y 1, entonces la expresión para provee el vector de parámetros para la probabilidad condicional de que dado cierto . La cantidad produce la probabilidad condicional de que dado cierto . Por lo tanto, para los pares, donde , la contribución a la función de verosimilitud es , y para aquellos pares en que , la contribución a la función de verosimilitud es . Una forma conveniente de expresar la contribución a la función de verosimilitud para el par , es la siguiente:
Dado que las observaciones se asume que son independientes, la función de verosimilitud se obtiene como el producto de los términos dados en la expresión anterior, como sigue:
El principio de máxima verosimilitud establece que se usa como estimadores de el valor que maximiza la expresión Sin embargo, es matemáticamente más sencillo trabajar con el logaritmo de la ecuación anterior. La expresión para el logaritmo de la verosimilitud es:
Para encontrar el valor del vector que maximiza , se diferencia con respecto a y , se igualan las ecuaciones a 0. Las ecuaciones resultantes son:
Estas expresiones no son lineales en los parámetros y , por lo que se requieren métodos especiales para su solución. En McCullagh y Nelder (1989), se puede obtener una explicación más amplia sobre los métodos iterativos usados para la solución de esas ecuaciones. Los valores de obtenidos con la solución de las ecuaciones anteriores, se llaman los estimadores de máxima verosimilitud y serán denotados por el símbolo
6.1 PRUEBA DE SIGNIFICACIÓN DE LOS COEFICIENTES
Una forma de probar la significación de los coeficientes de las variables en cualquier modelo, es contestando a la pregunta ¿el modelo que incluye la variable en cuestión dice más sobre la variable de respuesta, que aquel modelo que no la contiene?. Entiéndase que no se refiere a decir si los valores predichos por el modelo son una precisa representación de los valores observados en un sentido absoluto, a esto último se le llama Bondad del Ajuste.
En regresión logística el principio para medir la significación de los coeficientes es el siguiente: comparar los valores observados de la variable de respuesta con los predichos por el modelo, con y sin la variable en cuestión. En regresión logística, la comparación de los valores observados con los predichos, se hace con la función de verosimilitud:
Para mejor comprender esta comparación, es útil conceptualmente, pensar que un valor observado de la variable de respuesta es también un valor predicho resultante de un modelo saturado. Un modelo saturado es aquel que contiene tantos parámetros como datos observados,8. La comparación de los valores observados con los predichos, usando la función de verosimilitud esta basada en la siguiente expresión:
donde VMA es verosimilitud del modelo ajustado y VMS es verosimilitud del modelo saturado.Ala expresión entre corchetes en la fórmula anterior se le llama ratio de verosimilitud. Usando el doble negativo del logaritmo es necesario para obtener una cantidad cuya distribución es conocida y puede por lo tanto, ser usada para prueba de hipótesis. Esa prueba se llama, la prueba del ratio de verosimilitud.
Sustituyendo en
Se obtiene:donde
Al estadístico D lo llaman deviance en McCullagh y Nelder (1989). Este estadístico es para la regresión logística como la suma de residuos para la regresión lineal. Algunos softwares, tales como SAS reportan el valor del estadístico deviance, computado con la verosimilitud del modelo ajustado. Otros como el SPSS, reportan este estadístico usando el logaritmo de la función de verosimilitud, Visauta y Martori (2003).
Con el propósito de evaluar la significación de la variable independiente, se computa el valor de D con y sin la variable independiente en la ecuación. El cambio en D debido a la inclusión de la variable independiente en el modelo, se puede medir como:
G=D(Modelo sin la variable) – D(Modelo con la variable)
Como la verosimilitud del modelo saturado es común en ambos valores de D, se puede transformar la ecuación anterior a:
donde Verosimilitud sin la variable independiente y Verosimilitud con la variable independiente. Para el caso específico de una sola variable independiente, es fácil demostrar que cuando la variable no está en el modelo, la estimación de máxima verosimilitud para es , donde y y , el valor predicho por el modelo es . En este caso se puede expresar como:
Bajo la hipótesis de que es igual a 0, el estadístico G sigue una distribución chi cuadrada con un grado de libertad, suponiendo que se tiene una muestra de tamaño grande.
Se han propuesto otros estadísticos para hacer esta prueba de significación. Entre ellos tenemos la prueba de Wald. Los supuestos que deben cumplirse para esta prueba son los mismos que para la prueba del ratio de verosimilitud. Una discusión más completa de esta prueba y de los supuestos de la misma, se pueden encontrar en Rao (1973). Hauck y Donner (1977) examinaron el desempeño de la prueba de Wald, y encontraron que tiene un mal comportamiento, fallando para rechazar la hipótesis nula cuando el coeficiente es significativo.
Jennings (1986), también exploro la bondad de la significación de los parámetros usando la prueba de Wald en regresión logística, llegando a conclusiones similares a las de Hauck y Donner, por esta razón, el ratio de verosimilitud será la prueba usada en este trabajo para medir la significación de los coeficientes.
6.2 MODELO DE REGRESIÓN LOGÍSTICA MÚLTIPLE
Este modelo se refiere al caso en que contiene más de una variable independiente. Las variables independientes pueden ser discretas o continuas, pero el desarrollo que sigue se centrará en el caso en que todas las variables independientes son continuas. Considere un conjunto de p variables, denotadas por el vector . Hagamos la probabilidad condicional de que la variable de respuesta sea igual a . El logit del modelo de regresión logística múltiple es dado por la ecuación:
y el modelo de regresión logística es
Asumiendo que se tiene una muestra de n observaciones independientes , el ajuste del modelo requiere que se obtengan estimaciones del vector El método a emplear es el de máxima verosimilitud.
La función de verosimilitud es:
Habrán ecuaciones de verosimilitud que se obtienen diferenciando la función del logaritmo de la verosimilitud con respecto a los coeficientes. Las ecuaciones de verosimilitud resultantes son:
La solución de este conjunto de ecuaciones requiere software especial para su solución, tales como SPSS, SAS o MINITAB9.
Como se ha mantenido hasta ahora, el análisis se centrará en modelos con variables independientes continuas. Esta aclaración es necesaria por que en el caso de variables independientes discretas, la interpretación del modelo requiere un tratamiento especial10.
Cuando un modelo de regresión logística contiene variables independientes continuas, la interpretación de los coeficientes estimados depende de cómo se incluyeron en el modelo y las unidades particulares de dichas variables. Se asumirá que la función logit es lineal para desarrollar el método de interpretación de los coeficientes de las variables continuas.
El objetivo de la interpretación es ajustar estadísticamente el efecto estimado de cada variable en el modelo para diferencias en las distribuciones y de las asociaciones entre las mismas. Aplicando este concepto a un modelo de regresión logística multivariable, se puede resumir que cada coeficiente estimado provee una estimación del logaritmo de la probabilidad ajustado para todas las variables incluidas en el modelo.
En un modelo multivariable se hace necesario el estudio tanto del efecto de cada una de las variables individuales como el de las interacciones existentes entre ellas. La presencia o no del término independiente es otro ingrediente más a tomar en cuenta.
7. LOS ESTADOS DE CONTABILIDAD ANALÍTICOS
La fuente primaria para la evaluación y diagnóstico de los bancos comerciales, lo constituyen los Estados de ContabilidadAnalíticos. Estos estados se construyen a partir de las cuentas del manual de contabilidad, herramienta estándar que usan todas las entidades supervisadas por la Superintendencia de Bancos, para la remisión de sus informaciones financieras.
Las informaciones de estos estados de contabilidad son reportadas en detalle diariamente al día siguiente del corte del mismo. Este reporte contiene los balances de más de 5,000 cuentas, y a partir de esos balances se construyen: El Balance General, El Estado de Ganancias y Pérdidas, el Estado de Cartera, y los Indicadores de estructura.
La primera versión del manual estándar de cuentas se realizó en el 1995, y fue la respuesta para poder elaborar estados comparativos homogéneos. Antes de esa fecha, las entidades supervisadas usaban el catálogo de cuentas que mejor les parecía. Esto dificultaba tanto la revisión como la publicación de los boletines estadísticos periódicos.
Con la unificación del manual de cuentas, se logró la construcción de validadores automáticos, que pudieran hacer una revisión preliminar de las cifras, previo a su envío a la Superintendencia de bancos. La recepción de las informaciones se hace sin intervención humana, y la construcción de los productos que necesitan los analistas para la evaluación de las entidades se hace de forma tal que estos pueden solicitarlos a requerimiento mediante la utilización de un sistema, que les permite tener diferentes vistas de los datos de acuerdo al tipo de análisis a realizar.
La mayoría de las informaciones necesarias para hacer una evaluación cuantitativa de la entidad financiera está disponible en los balances del manual de cuentas. Hay otras informaciones de carácter cualitativo, que no están ahí disponibles, pero que están a disposición del analista a través de otras fuentes de información.
Tradicionalmente estas han sido las fuentes de información para la evaluación de las entidades financieras. El proceso de evaluación consume mucho tiempo por parte de los analistas, por lo que se limitan a hacer evaluaciones más frecuentes de las entidades con potencial para impactar de forma más contundente el sistema financiero en caso de dificultad, los Bancos Comerciales. Los demás tipos de entidades, Asociaciones de Ahorros y préstamos, financieras, Bancos de Desarrollo, etc. se evalúan con una frecuencia más espaciada o cuando hay algún tipo de evento que justifique su revisión (por ejemplo los resultados de inspecciones in situ, denuncias de terceros, etc.).
7.1 INDICADORES FINANCIEROS
Los indicadores financieros son las herramientas primarias usadas por los analistas para resumir el cúmulo de informaciones que les llegan de los bancos. Les permite tener una visión panorámica de las entidades, y les orienta para determinar que tipos de análisis más profundos deben realizar.
Dependiendo del tipo de diagnóstico a realizar, los indicadores tendrán una conformación particular. Igualmente, dependiendo del tipo de empresa a evaluar, los indicadores financieros se construirán de manera especial. Es decir, a pesar de usar las mismas informaciones contables, son diferentes los indicadores financieros necesarios para la evaluación de una empresa de manufactura, que los de una empresa de servicios, o un banco. Dentro de las empresas financieras, no son los mismos indicadores los necesarios para evaluar un banco que una casa de préstamos de menor cuantía.
En esta investigación se usarán los indicadores de estructura para la evaluación de los bancos comerciales. Los indicadores de estructura se construyen a partir de las cuentas del manual de contabilidad y de los resúmenes contenidos en los Estados de Contabilidad Analíticos. Estos indicadores de estructura son:
Estructura de Activos
• Disponibilidades/Activos
• Cartera de Créditos/Activos
• Inversiones/Activos
• Activos Fijos/Activos
• Bienes Recibidos en Recuperación de Créditos/Activos
• OtrosActivos/Activos
• Cartera de Créditos Vigentes + Inver./Activos
Estos indicadores miden la participación de los principales componentes del activo del banco como parte de los activos totales.
Estructura de Pasivos
• Total Captaciones/Pasivos + Patrimonio
• Otros Pasivos/Pasivos + Patrimonio
• Capital en Circulación + Reserva Legal/Pasivos + Patrimonio
• Patrimonio/Pasivos + Patrimonio
Los indicadores de estructura de pasivos, miden como esta el apalancamiento del banco con respecto a su patrimonio.
Estructura y Calidad de Cartera
• Cartera de Créditos Vigentes/Cartera de Créditos
• Cartera de Créditos Vigentes M/N /Cartera de Créditos
• Cartera de Créditos Vigentes M/E /Cartera de Créditos
• Cartera de Créditos Vencidos/Cartera de Créditos
• Provisión para Cartera de Créditos/Cartera de Créditos
Estos indicadores miden la exposición al riesgo crediticio que esta asumiendo el banco en su cartera de crédito, tanto en moneda nacional como extranjera.
Liquidez
• Disponibilidades/Total de Captaciones
• Disponibilidades/Total Captaciones + Oblig. Con Costo
• Disponib.+ Inversiones en Depósitos y Valores/Total Activos
• Activos Productivos/Total Captaciones + Oblig. Con Costo
Los indicadores de liquidez evalúan el grado de preparación que tiene el banco para hacer frente a sus compromisos inmediatos en el corto plazo. Estos son indicadores muy importantes, ya que pueden ser la razón del colapso de una entidad si no se enfrenta la causa de falta de liquidez con oportunidad.
Estructura de Gastos grales. y de Administración
• Sueldos y compensaciones. al personal/Total Gastos grales. yAdmtivos
• Otros Gastos generales/Total Gastos grales. y Admtivos
• Total Gastos grales. y Admtivos/Total Gastos
Los indicadores más efectivos para medir la gestión de la gerencia de los bancos, son los indicadores de gastos administrativos. Sirven para medir como están siendo usados los recursos generados por las actividades de la entidad.
Otros Indicadores
• Activos Productivos/Total Pasivos
• Rendimiento Financiero/Activos Productivos
• Gastos Financieros/Total Captaciones + Oblig. Con Costo
• Total Gastos grales. y Admtivos /Total Captaciones + Oblig. Con Costo
• Rentabilidad Patrimonial
Por último, existen otros indicadores complementarios que ayudan a tener una visión combinada de los anteriores.
Estos indicadores se construyen con las cifras remitidas por los bancos comerciales diariamente. A pesar de que son indicadores cuantitativos, y por lo tanto, no son suficientes para hacer una evaluación exhaustiva de una entidad financiera, pueden ser muy útiles para una primera evaluación preliminar que sirviera de alerta para un análisis más profundo por parte de los analistas, usando las mismas informaciones y otras fuentes de datos de tipo cualitativos.
8. DESARROLLO DEL MODELO DE REGRESIÓN LOGÍSTICA
Para el desarrollo del modelo de regresión logística se usaron las cifras de los indicadores de estructura mensuales de los bancos comerciales desde noviembre del 2002 a diciembre del 2004. Durante ese periodo tres bancos comerciales colapsaron (Baninter, Bancredito y Mercantil) y esta fue la información primaria utilizada para la clasificación de los indicadores en dos categorías, bancos viables y bancos inviables.
El hecho de que la clasificación se realizara con información histórica, despeja la duda de si el criterio utilizado para la clasificación pudiera tener algún grado de subjetividad. Reduce, aunque no descarta el papel de un buen analista financiero para la evaluación de los bancos, y puede ser comprobada la bondad del modelo con las cifras, también históricas del año 2005.
No se cuestiona la utilidad de los indicadores usados en la construcción del modelo, ya que los mismos han demostrado sobrada capacidad cuantitativa para dar señales de alerta cuando una entidad pudiera estar en peligro de viabilidad. Su conformación es similar a la de los indicadores CAMEL recomendados por el comité de Basilea.
Se tomaron los indicadores mensuales de los diferentes bancos comerciales, que a noviembre de 2002 lo conformaban 14 bancos. Por información posterior11 al colapso de los bancos se sabe que para esa fecha los bancos: Baninter, Bancredito y Mercantil, estaban manejándose de forma inapropiada.
A los bancos colapsados se les asignó un código de estatus igual a 1, mientras que a los demás bancos se les asigno en el mismo código el valor de 0. Esto se repitió en todos los meses hasta diciembre de 2004. A pesar de que el banco Profesional adquirió a Bancredito a mediados del 2003, continuaron operando separadamente hasta marzo del 2005, por lo que, el banco Profesional se siguió considerando como un banco separado del Bancredito en la asignación de códigos de estatus hasta diciembre del 2004.
8.1 EVALUACIÓN DEL MODELO
Después de preparar los datos con los indicadores y el código de estatus, se procedió a correr un modelo de regresión logística usando el software estadístico SPSS versión 11.5. Se utilizó la opción forward Wald para la selección de las variables a ser incluidas en el modelo. Esta opción va seleccionando las variables (indicadores) a incluir en el modelo según el criterio de cual tiene el mejor estadístico de Wald.
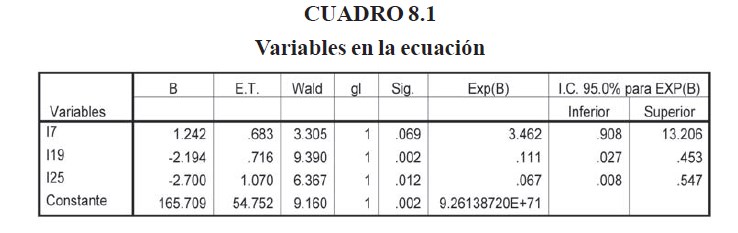
En el cuadro 8.1 se puede observar el resultado de la regresión. Las variables incluidas en el modelo son:
I7 = (Cartera de Créditos Vigentes + Inversiones)./Activos
I19 = (Disponibilidades+ Inversiones en Depósitos y Valores) /Total Activos
I25 = (Activos Productivos) /Total Pasivos
El primero es parte de los indicadores de estructura de activos, el segundo y el tercero son de los indicadores de liquidez. No es inesperado que estos indicadores formen parte del grupo de indicadores que ayuda a diferenciar los bancos en problemas de los que están viables, ya que los estudios de Guzmán y otros (2005) señalan la mala composición de la cartera y el consecuente resultado en la liquidez, como los detonadores de la crisis de los bancos estudiados.
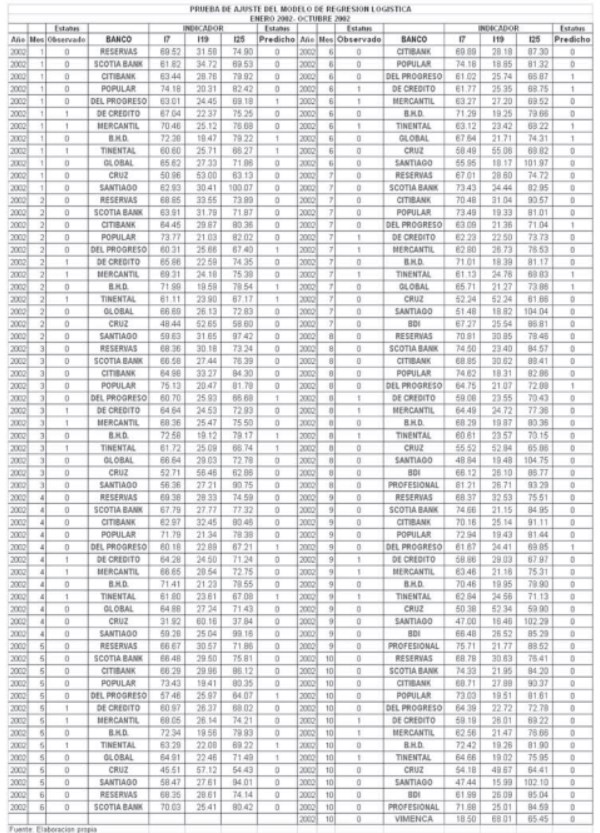
Es interesante que de los 30 indicadores sometidos al SPSS para la selección de las mejores variables explicativas, sólo 3 tengan el poder de predicción suficiente para diagnosticar a los bancos con problemas. El valor del p-value para el indicador I7 fue de 0.069, como se puede observar en el cuadro 8.1, sin embargo, los resultados de la predicción fueron muy alentadores con este indicador incluido en el modelo. En el cuadro 8.2 se puede apreciar el resultado de la clasificación predicha por el modelo para los datos del período de estudio.
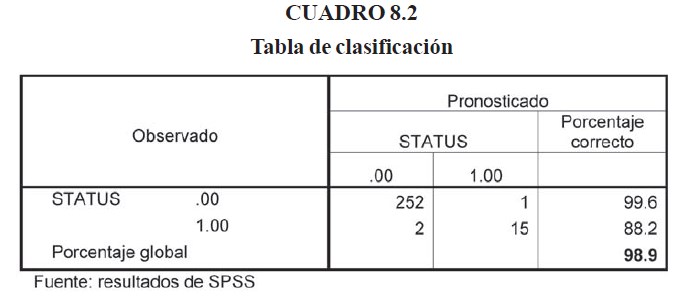
Interpretando los resultados del cuadro 8.2, vemos que el modelo obtuvo un 98.9% de precisión en las predicción del estatus de los bancos con relación a los datos observados, es decir, sólo hubo un error de 253 casos donde los bancos con estatus 0, el modelo le asigno estatus 1, y de 17 casos con estatus 1, el modelo asigno erróneamente 2 con estatus 0.
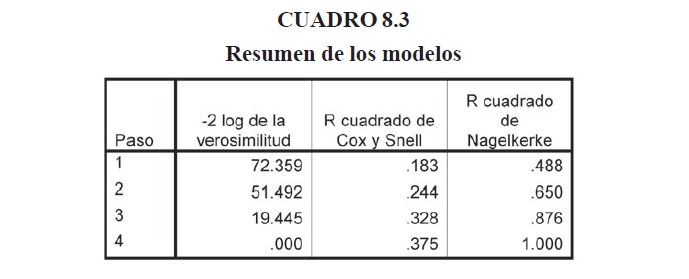
En el cuadro 8.3 se resume los indicadores de bondad del ajuste en las 4 iteraciones de solución del modelo. Como se puede apreciar los tres parámetros son cada vez mejores a medida que el modelo se va refinando. El valor del logaritmo de la verosimilitud se reduce hasta cero, indicando que la misma esta maximizada.
El cuadro 8.4 muestra los resultados de la prueba de Hosmer y Lemeshow para los 4 pasos de refinamiento del modelo.

Hosmer y Lemeshow (1980), demostraron que cuando el modelo de regresión lineal es el correcto, el estadístico de prueba se distribuye con una distribución X2
El cuadro 8.4 indica que el modelo es el adecuado ya que el nivel de significación para la prueba es más de 90% desde el primer paso de refinamiento del modelo. Estos mismos autores no recomiendan el uso de esta prueba cuando el número de casos es menor de 400, como en este estudio, por lo que se hicieron evaluaciones alternas para verificar la bondad del modelo.
En el cuadro 8.3 se muestran los resultados del cálculo del R2 de Cox y Snell y el R2 de Nagelkerke. Estos estadísticos son una versión para la regresión logística del coeficiente de regresión para la regresión lineal.
El R2 de Cox y Snell no puede llegar a 1, pero mientras más alto mejor. Por otro lado el R2 de Nagelkerke si puede llegar a 1 y en este caso, señala que hay una regresión perfecta. Las siguientes son las ecuaciones de ambos estadísticos:
LLnull es el log likelihood (logaritmo de la verosimilitud) del modelo sólo con la constante y LLk es el log likelihood con las demás variables incluidas.
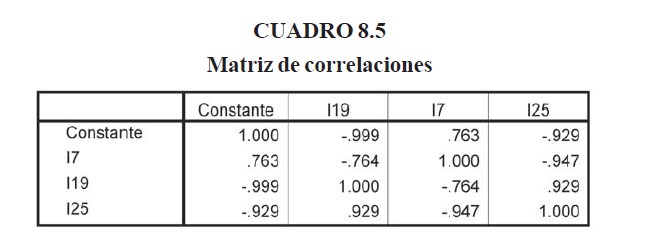
En el cuadro 8.5 se muestra la matriz de correlaciones de los parámetros del modelo, al final del cuarto paso de refinamiento del modelo. Se puede destacar la alta correlación entre la constante y dos de los indicadores, I19 e I25, esto pudiera implicar un problema de multicolinealidad.
En el cuadro 8.6 se muestran los resultados de las pruebas de los coeficientes del modelo en cada uno de los cuatro pasos de refinamiento del mismo. Se puede observar que en todos los pasos, la prueba indica que los coeficientes están bien seleccionados, ya que esta prueba indica que las variables incluidas en el modelo, en su conjunto, tienen coeficientes diferentes de cero. Este resultado viene a confirmar los mostrados en la tabla 8.1 en los estadísticos Wald.

La diferencia observada en cada paso, en el estadístico , se debe a que las variables son incluidas una a la vez. Por eso sólo coinciden en el bloque y el modelo.
8.2 RESULTADO DE LAS PRUEBAS
Se han propuesto varios métodos para medir la efectividad de modelos de regresión lineal, Oelerich et al (2006). En síntesis estos métodos de evaluación miden que tan bien el modelo puede predecir las probabilidades de los casos conocidos. En este estudio se compara la predicción de inviabilidad hecha por el modelo con la información conocida sobre el desempeño de los bancos en un periodo dado.
Oelerich y Poddig (2006) proponen un índice para cuantificar la calidad de la clasificación binaria entre viable y no viable de empresas sujetas de crédito que se puede utilizar para los bancos comerciales. Este índice es la proporción de bancos correctamente clasificados a partir de información a posteriori. Recuérdese que se les asigno un estatus 0 a los bancos viables y 1 a los no viables.Si representa el estatus real de cada banco en el mes k y el estatus predicho por el modelo, donde entonces, el índice de clasificación será:
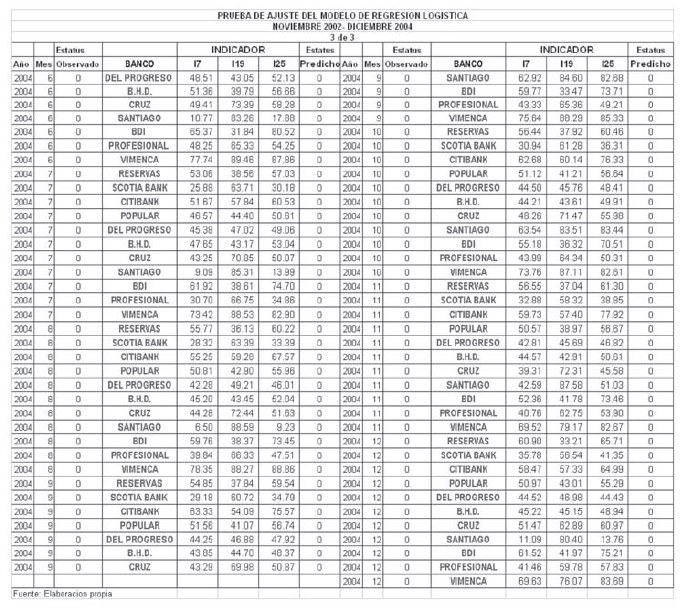
El índice de clasificación para el período noviembre 2002-diciembre 2004, periodo a partir del cual se construyó el modelo, fue de 0.9899. La verdadera prueba para este índice es la realizada con los datos comprendidos entre enero 2002-octubre 2002, y enero 2005-diciembre 2005, ya que se cuenta con información del desempeño de los bancos en esos dos periodos.
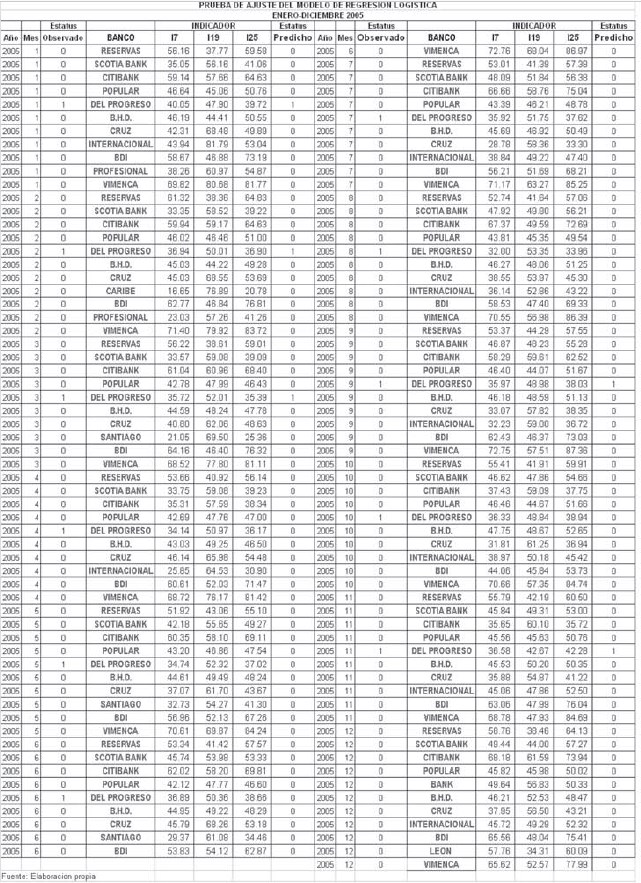
Para el periodo enero 2002-octubre 2002 el índice de clasificación fue 0.704. En el periodo enero 2005-diciembre 2005, sólo un banco presento problemas de inviabilidad, y este fue recuperado mediante una inyección de capital por parte de los accionistas. Aunque este banco no colapso, se le asigno el código 1 en el estatus del mismo durante todo el año 2005, con fines de medir la efectividad del modelo para predecir problemas en los bancos. En este periodo el índice de clasificación fue 0.9512.
La notable diferencia observada en el índice de clasificación en los dos periodos de pruebas pueden deberse a las siguientes razones:
• Los bancos Bancredito y Mercantil (bancos donde el modelo reflejó errores de clasificación durante el 2002) no reflejaban adecuadamente sus informaciones contables, reportando estados financieros alterados a las autoridades durante el año 2002.
• Baninter estaba en un proceso de venta con el banco del progreso, lo que contribuyó a que las informaciones reportadas a la Superintendencia de bancos fueran más claras aunque no suficientemente claras en lo concerniente a las captaciones y los créditos a empresas vinculadas.
• El sistema de supervisión fue mejorado notablemente a partir de la crisis del 2003, implementándose nuevos mecanismos para el reporte de información y realizando auditorias de sistemas e inspecciones asistidas por organismos internacionales que ayudaron a esclarecer el panorama.
Es digno de resaltar el hecho de que en el periodo comprendido de enero a octubre del 2002, el modelo asigno el estatus 1 en varios meses al banco del Progreso12. Informaciones aparecidas en la prensa del 19 de abril del 200613, dan cuenta de los resultados de auditorias realizadas durante ese lapso de tiempo, donde se revelan problemas de ocultamiento de información en las que incurrió el banco, con la finalidad de engañar a la Superintendecia de Bancos.
9 CONCLUSIONES Y RECOMENDACIONES
Este estudio demuestra la factibilidad de usar la regresión logística para hacer el diagnóstico de instituciones financieras, específicamente, bancos comerciales. Los resultados de las pruebas realizadas son muy alentadores y señalan un amplio campo de posibilidades para la construcción de modelos que permitan hacer de manera automática y rápida la evaluación de las entidades supervisadas, resaltando aquellas que ameriten un estudio más profundo de parte de los analistas.
La experiencia durante la construcción del modelo indica que este debe ser sometido a un proceso de refinamiento continuo, alimentado por los resultados de las evaluaciones de los analistas, con el objetivo de que el mismo pueda servir para detectar anomalías antes del colapso de la entidad estudiada.
El proceso de refinamiento pudiera conducir a diagnósticos mucho más estructurados, incluso, asignando varias categorías a la entidad y no sólo dos (viable o no viable). La regresión logística permite construir modelos capaces de determinar esta estratificación de la variable respuesta.
Aunque el modelo se construyó en base a información histórica de dominio público, este pudiera ser mucho más rico si pudieran incluirse informaciones que son del conocimiento exclusivo de las entidades supervisoras. Por ejemplo, hay bancos que han presentado dificultades que no se ven reflejadas inmediatamente en las informaciones financieras publicadas periódicamente. De tomarse en cuenta estos datos durante la construcción del modelo, este pudiera tener mayor efectividad como herramienta de alerta temprana.
La Superintendencia de Bancos dedica muchas horas de trabajo de sus analistas a hacer la evaluación de las informaciones que llegan de las entidades supervisadas. Muchas veces ese análisis concluye de manera favorable para la entidad financiera, lo cual es muy bueno, pero igualmente el tiempo invertido no es recuperable. Por otro lado, entidades que ameritan un escrutinio más profundo, son evaluadas en el lapso de tiempo restante, con lo que el análisis de toda la información recibida debe hacerse de forma racionalizada.
Con este nuevo recurso, la Superintendencia puede hacer el análisis de “todas” las entidades en tiempo mínimo, y las entidades que ameriten más tiempo, podrán contar con el mismo, ya que sólo las que el modelo señale como en problemas, serán revisadas a mayor profundidad.
El modelo de diagnóstico puede ser mejorado incorporando otros criterios de evaluación que se utilizarían de manera conjunta con la regresión logística para tener, digamos una segunda opinión, y así reducir las posibilidades de falsas alarmas.
Dado que la información utilizada en la construcción del modelo, corresponde a reportes mensuales, y considerando que también se reciben informaciones diarias, el modelo podría ser evaluado utilizando la información más frecuente, para así tener diagnósticos más oportunos.
El modelo obtenido tiene un marcado defecto, y es que se hizo con poca información, a penas 297 casos. En situaciones como esta, el procedimiento recomendado por Oelerich y Poddig (2006), pudiera ser una solución a este dilema. Estos autores usaron la simulación y la metodología bootstrap, para edificar un modelo estadísticamente más robusto, reduciendo la variabilidad de las predicciones.
El modelo presentado mostró indicios de multicolinealidad que pudiera ser un problema desde el punto de vista estadístico, sin embargo, los resultados de las pruebas con las informaciones en los periodos de estudio, hacen que este defecto sea sobrellevado.
Notas
- Comité de Basilea para la Supervisión Bancaria (1997).
- TBerg (2004).
- Superintendencia de Bancos de la Rep. Dom. (2004).
- El enfoque presentado en esta obra es desde el punto de vista de análisis multivariado, por lo que se plantean las ventajas y desventajas de la regresión logística en este contexto.
- Trippi, R. and Turbain, E.,(1996), evalúan también el uso de las redes neuronales en clasificación. Los resultados son variados cuando se comparan con los de la regresión logística.
- Visauta y Martori (2003).
- Este libro es una fuente riquísima para el estudio de la regresión logística. Los fundamentos teóricos son tratados con mucho detalle.
- Hosmer y Lemeshow (2000).
- Vease Ryan, B. and Joiner, B.,(2001) y Visauta, B. y Martori, J.C., (2003).
- Vease Breslow and Day (1980), Kelsey, Thompsonand Evans (1986) y Rothman, Greenland (1998) and Schlesselman (1982).
- Guzman, J.F., Livacic, E., Mauch, C. y Ortiz, M., (2005), “Informe del Panel de Expertos Internacionales: Crisis Bancaria República Dominicana”, Banco Central de la República Dominicana, Santo Domingo.
- Ver anexo 2, resultados de pruebas.
- Periódico vespertino “El Nacional” del 19 de abril del 2006, página 9.
BIBLIOGRAFÍA
1. Agresti, A., (2002), Categorical Data Analysis (Wiley Series in Probability and Statistics), John Willey & Sons Inc., Hoboken, New Jersey.
2. Aldrich,J.H. and Nelson, F.D., (1984), Linear Probability, Logia and Probit Models. Beverly Hills: Sage Publications.
3. Anónimo, (2006), “Progreso informa Supuestas Anomalías”, El Nacional, 19 de abril del 2006, pp 9.
4. BBVA, (2002), Rating de Empresas. Desarrollo y Calibración de una Herramienta de rating.
5. Berg, A., Borenztein, E. and Patillo, C., (2004), “Assessing early warning systems: How have they worked in practice”, International Monetary Fund.
6. Breslow, N.E. and Day, N.E., (1980), “Statistical Methods in Cancer Research”, Vol. 1 : The Analysis of case-control studies. InternationalAgency on Cancer, Lyon, France.
7. Collet, D. (2003), Modelling Binary Data. Second Edition. London: Chapman and Hall.
8. Cox, D.R. and Snell, E. J., (1989), Analysis of Binary Data. Second edition. Chapman & Hall, London.
9. Fienberg, S.E., The Analysis of Cross-Classified Categorical Data. Second edition. MIT Press. Cambridge Massachusetts.
10. Fox, J. (1997), Applied Regression Analysis, Linear Models, and Related Methods. Thousand Oaks CA: Sage Publications.
11. Guzman, J.F., Livacic, E., Mauch, C. y Ortiz, M., (2005), “Informe del Panel de Expertos Internacionales: Crisis Bancaria República Dominicana”, Banco Central de la República Dominicana, Santo Domingo.
12. Hauck, W.W. and Donner, A. (1977), “Wald´s test as applied to hypotheses in logit analysis”. Journal of the American Statistical Association, 72, 851- 853.
13. Hinkley, D.V., Reid, N. and Snell, E.J., Statistical Theory and Modeling: in Honour of Sir David Cox. FRS London: Chapman and Hall.
14. Hosmer, D., Lemeshow, S., (1980), “A goodness of fit test for the multiple logistic regression model”. Communications in Statistics, A10, 1043-1069.
15. Hosmer, D., Lemeshow, S.,(2000), “Applied Logistic Regression”, Wiley- Interscience; 2nd edition.
16. Huang, Z., Chen, H., Hsu, C., Chen, W., and Wu, s., (2004), “Credit rating analysis with support vector machines and neural networks: A market comparative study. Decision Support Systems. 37, pp. 543-558.
17. Jennings, D.E., (1986), “Judging inference adequacy in logistic regression”, Journal of The American Statistical Association, 81, 471-476.
18. Kelsey, J.L., Thompson, W.D., and Evans, A.S. (1986), “Methods in Observational Epidemiology”, Oxford University Press, New York.
19. Liao, J.G., McGee, D., (2003), “Adjusted Coefficients of Determination for Logistic Regression”, The American Statistician, Vol. 57, no. 3, pp. 161-165.
20. Long, J.S. (1997), Regresión Models for categorical and Limited Dependent Variables. Thousand Oaks CA: Sage Publications.
21. McCullagh, P. and Nelder, J.A., (1989), Generalized Linear Models. Second Edition. Chapman & Hall, London.
22. Oelerich, A. and Poddig, T., (2006), “Evaluation of rating systems”, Expert Systems with Applications 30, pp. 437-447.
23. Peña, D., (2002), Análisis de Datos Multivariantes, McGraw Hill, Madrid.
24. Rao, C. R., (1973), Linear Statistical Inference and Its Applications, Second Edition. Wiley, Inc., New York.
25. Rothman, K.J., and Greenland, S., (1998), Modern Epidemiology, Third Edition. Lippincott-Raven, Philadelphia.
26. Ryan, B. and Joiner, B.,(2001), Minitab Handbook, Duxbury Thomson Learning, Canada.
27. Salchenberger, L.M., Cinar, E.M., Lash, N.A., (1992). Neural Networks: A New Tool for Predicting Thrift Failures. Decision Sciences, 23, No. 4. July/ August, pp. 899-916.
28. Shlesselman, J.J., (1982), Case-Control Studies. Oxford University Press, New York.
29. Trippi, R. and Turbain, E.,(1996), Neural Network in Finance and Investing, McGraw Hill, New York.
30. Vapnik, V and Chapelle, O. (2000), “Bounds on Error Expectation for Support Vector Machines”, Neural Computation 12(9): 2013-2036.
31. Visauta, B. y Martori, J.C., (2003), Análisis Estadístico con SPSS para Windows. Volumen II, Estadística Multivariante. McGraw Hill/Interamericana de España.