Ciencia y Sociedad, Vol. 33, No. 1 Enero-Marzo 2008: p.29-46, • ISSN: 0378-7680 (impresa) • ISSN: 2613-8751 (en línea) • Sitio web: https://revistas.intec.edu.do/

ANALISIS DE SEÑALES VIBRATORIAS

DOI: http://dx.doi.org/10.22206/cys.2008.v33i1.pp29-46

María Penkova Vassileva*

* Area de Ingeniería, INTEC, Santo Domingo Email: mariap@intec.edu.do

Cómo citar: Penkova Vassileva, M. (2008). Análisis de señales vibratorias. Ciencia y Sociedad, 33(1), 29-46. https://doi.org/10.22206/cys.2008.v33i1.pp29-46

Resumen

Análisis de vibraciones es una de las prácticas más usadas del mantenimiento predictivo y requiere un conocimiento de las señales y su análisis es usno de los pilares fundamentales de la Ingeniería La información que contienen las señales debe transformarse dependiendo de los propósitos de estudio.

Este trabajo se refiere a la descripción de diversas técnicas matemáticas de procesamiento de las señales con enfoque al análisis de vibraciones para el diagnóstico de la condición de las maquinarias rotatorias.

Palabras clave:

Información, señales, vibraciones, análisis

La mayoría de las industrias del mundo que desarrollan programas de mantenimiento predictivo utilizan el monitoreo y análisis de las vibraciones para establecer en qué estado está la salud mecánica de las máquinas y especialmente la de sus elementos más críticos para poder prevenir fallas catastróficas.

Para estudiar mejor las diferentes causas de las vibraciones en los sistemas debemos crear simples modelos dinámicos y matemáticos que los describen. Sobre el comportamiento vibracional de los sistemas influyen tanto sus características constructivas como sus características de trabajo. Las vibraciones en los sistemas serán reflejo de su comportamiento dinámico.

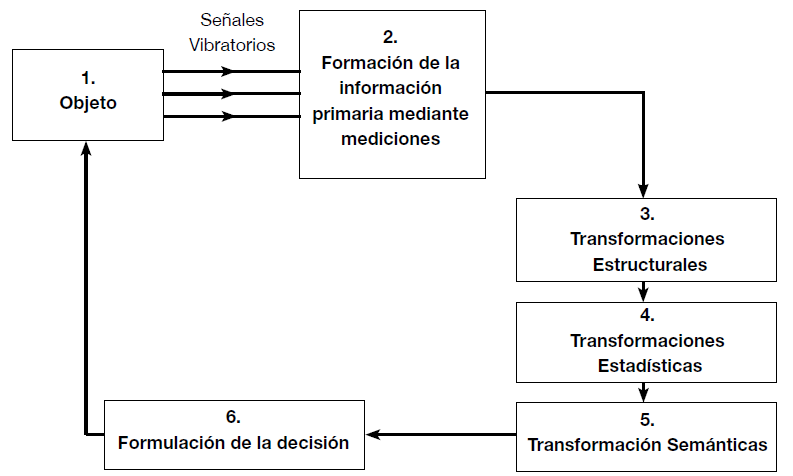
El análisis de las vibraciones presenta cambio consecutivo de la información contenida en el estado del objeto (véase figura 1). La información es una categoría abstracta pero siempre se presenta en forma de señales. La señal es la variación de un parámetro físico en función del tiempo y transporta cierta cantidad de información desde un emisor (la máquina objeto de estudio (1)) hasta un receptor (aparatos de medición) a través de los cuales se ejerce la primera transformación de las señales obtenidas (etapa 2). El ruido en las señales (la información inútil) se separa en las etapas 3, 4 y 5 a través de métodos técnicos. Las transformaciones estructurales en la información se llevan a cabo a través de normalización, cuantización y discretización, descomposición y sintetización.

A través de las transformaciones estadísticas se separa el residuo estadístico en la información y las transformaciones semánticas separan el contenido semántico y la información semántica da lugar a la evaluación diagnóstica.

La tarea del especialista en análisis de vibraciones es poder identificar y determinar los fenómenos vibratorios en los sistemas mecánicos midiendo los parámetros vibracionales a través del procesamiento y análisis de las señales emitidas por los mismos durante su funcionamiento.

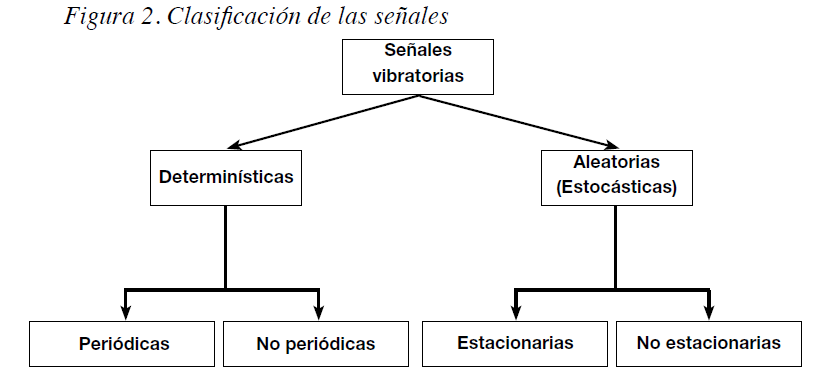
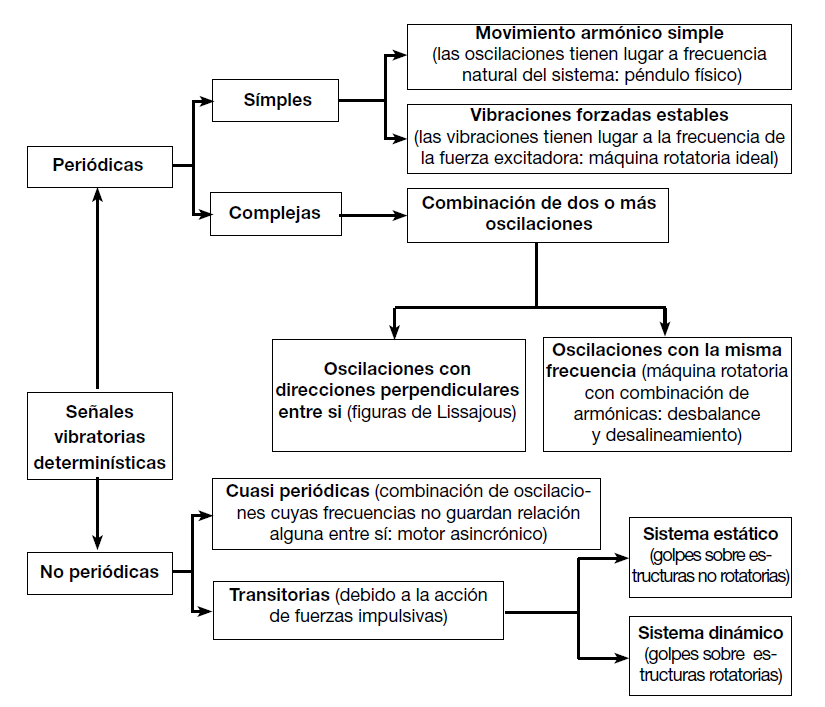
Desde el punto de vista de la cinemática las señales en general se dividen en dos grandes grupos (véase figura 2): determinísticas (aquellas que representan fenómenos que pueden ser descritos analíticamente de manera exacta mediante una expresión matemática relativamente sencilla; véase figura 3) y aleatorias o estocásticas (no es posible describirlas analíticamente con una expresión explícita simple como en el caso anterior; véase figura 4). Sin embargo, cuando una señal estocástica se observa durante un largo periodo de tiempo puede verse cierta regularidad y puede ser descrita en términos de probabilidades y promedios estadísticos.

Análisis de señales determinísticas

Las señales vibratorias se representan a través de la función analítica

(1) X = x (Ω, t)

que constituye el paquete total de información – evento, espacio, tiempo, que permita el uso de análisis de funciones en el tiempo $x_{i} = x_{i} (t), i = 1, 2, 3, . ., n,$ recibidas en n diferentes puntos del objeto de estudio.

En la transformación estructural la señal vibratorio compuesto puede presentarse como suma de funciones analíticas elementales $φ_{k} (t); K = 0, 1, 2, 3,$ ..., cuyas propiedades son previamente conocidas:

(2) x (t) = {\sum C_{k}}_{k = 0}^{\infty} φ_{k} (t),

donde: $C_{k}$ son coeficientes de la descomposición.

Esto es posible porque el estado vibratorio del objeto mayormente es resultado de la transformación lineal de las fuerzas que actúan y de este modo se puede aplicar el principio de superposición que define la independencia de la transformación de la acción de cada de las fuerzas.

La información de la total acción de las fuerzas, contenida en la señal vibratoria se puede descomponer a elementos cuales caracterizan por separadamente toda acción de las fuerzas y de esta manera se puede determinar si esto es el resultado del funcionamiento correcto o se debe a alguna falla. Hacia las funciones elementales analíticas $φ_{k} (t); K = 0, 1, 2, 3,$ ..., dentro del intervalo de tiempo $[t_{ο}, t_{ο} + T]$ , en el cual se hace análisis de la señal vibratorio, se introduce la condición que deben ser además de ortogonales, también y normalizadas. Esto significa que el producto escalar entre las funciones cumple con la condición:

(3) \int_{t_{0}}^{t_{0} + T} φ_{k} (t) φ_{e} (t) d t = \{\begin{cases} C_{k} & 1, s i K = e \\ 0 & s i K \neq e \end{cases}

La condición de ortogonalidad define la independencia lineal entre las funciones analíticas y la condición de normalización define la posibilidad de que se pueden emplear como unidades estructurales elementales. Estas dos condiciones son analógicas a las condiciones de ortogonalidad y normalización hacia los vectores unitarios con cuales se construye el sistema de coordenadas ortogonal. Si usamos esta analogía

la transformación estructural de la señal vibratoria $x (t) = \sum_{K = 0}^{\infty} C_{K} φ_{K} (t),$

puede ser considerada como representación de $x (t)$ en forma de vector con componentes $C_{0}, C_{1}, C_{2},$ ... en un sistema de coordenadas ortogonales construida con los vectores unitarios $ψ_{k} (t)$ .

Los coeficientes $C_{k}$ de cada vector $C$ representan su proyección sobre el eje correspondiente. Analíticamente el producto escalar a través del cual se obtienen los coeficientes $C_{k}$ de la descomposición por funciones ortogonales $φ_{k} (t)$ llamados coeficientes generalizados de Fourier, es:

(4) C_{k} = \int_{t_{0}}^{t_{0} + T} x (t) φ_{k} (t) d t .

La elección de la forma de las funciones analíticas se define a través de las propiedades buscadas como, por ejemplo, minimizar el error promedio cuadrático de un número finito de elementos $n$ :

(5) ε^{2} (t) = {[x (t) - \sum_{k = 0}^{\infty} C_{k} φ_{k} (t)]}^{2} \Rightarrow \min

Se ha mostrado que el error mínimo del promedio cuadrático de toda función periódica se minimiza al descomponerla en serie de Fourier de funciones trigonométricas:

1, \cos ω_{0} t, \cos 2 ω_{0} t, \cos 3 ω_{0} t, . . ., \cos K ω_{0} t y s e n ω_{0} t, s e n 2 ω_{0} t, s e n 3 ω_{0} t, . . ., s e n K ω_{0} t

Usando la formula de Euler $e^{i \infty} = \cos α + isenα$ , la serie de funciones trigonométricas puede escribirse en forma compleja a través de las funciones:

1, e^{i 2 ω_{0} t}, e^{i 2 ω_{0} t}, e^{i 3 ω_{0} t}, . . ., e^{i K ω_{0} t}

La señal más simple es la señal periódica armónica cual puede describirse mediante la función dependiente del tiempo $t$ :

(6) x (t) = A s e n (ω_{0} t + θ)

donde: $A$ es la amplitud

$ω_{0}$ es la frecuencia angular en $s^{- 1}$

$θ$ es la fase inicial

Las señales armónicas satisfacen la condición de periodicidad: $x (t) = x (t + T)$ y la frecuencia angular que corresponde al periodo de la señal vibratoria, llamada frecuencia angular natural, es: $ω_{0} = \frac{2 π}{T}$

Las señales periódicas se pueden desarrollar en serie de Fourier:

x (t) = \frac{a_{0}}{2} + \sum_{k = 1}^{\infty} [a_{k} \cos (k ω_{0} t) + b_{k} \sin (k ω_{0} t)] a_{k} = \frac{2^{}}{T} \int_{- T / 2}^{T / 2} x (t) \cos (K ω_{0} t) d t, b_{k} = \frac{2}{T} \int_{- T / 2}^{T / 2} x (t) \sin (K ω_{0} t) d t, K = 0, 1, 2, . . . .

Esta serie puede ser escrita en la forma:

x (t) = C_{0} + \sum_{k = 1}^{\infty} C_{k} \cos (K ω_{0} t - θ_{k}) C_{0} = \frac{a_{0}}{2}, C_{k} = \sqrt{a_{k}^{2} + b_{k}^{2}}, θ_{k} = a r c t g \frac{b_{k}}{a_{k}}, K = 1, 2, . . . .

o en la forma compleja:

x (t) = \sum_{k = - \infty}^{\infty} C_{k}^{*} e^{i k ω t} C_{k}^{*} = \frac{1}{T} \int_{- T / 2}^{T / 2} x (t) e^{- i k ω t} d t

Las señales cuasi periódicas son las señales cuales tienen espectro discreto y para sus líneas espectrales $ω k$ no se puede encontrar frecuencia $ω 0$ a través de cual se podrían representar la frecuencias de las líneas espectrales $ω k = ωο, con K = 1, 2, 3, . . . .$

Las señales no periódicas pueden tratarse como periódicas para $T \to \infty$ . En este caso la serie de Fourier se transforma en integral de Fourier

(si T \to \infty, ω_{0} = \frac{2 π}{T} \to 0)

Los coeficientes de Fourier se convierten desde una serie de valores $C_{k}^{*}$ , $K = 0, 1, 2, 3, . . . .$ formando el espectro discreto en una función continua $C^{*} (ω)$ llamada densidad del espectro complejo.

Sentido físico de los coeficientes de Fourier $C_{k}^{}$ y de la densidad espectral $C_{}^{} (ω)$ .

La energía de un proceso real cualesquiera $x (t)$ en el intervalo de tiempo $T$ es

(11) E = \int_{- T / 2}^{T / 2} x^{2} (t) d t

La potencia media del proceso sería

(12) p = \lim_{T \to \infty} \frac{E}{T} = \lim_{T \to \infty} \frac{1}{T} \int_{- T / 2}^{T / 2} x^{2} (t) d t

Según el teorema de Parseval

(13) \frac{1}{T} \int_{- T / 2}^{T / 2} x^{2} (t) d t = \frac{1}{4} a_{0} + \frac{1}{2} \sum_{K = 1}^{\infty} (a_{K}^{2} + b_{K}^{2}) = \sum_{K = - \infty}^{\infty} {|C_{K}|}^{2}

La interpretación geométrica del teorema de Parseval muestra que el cuadrado de la longitud de cada vector no se cambia en una transformación lineal del sistema de coordinadas.

Desde el punto de vista físico este teorema muestra que la potencia media de la señal se puede recibir como suma de los coeficientes de la serie de Fourier. El espectro ${|C_{K}|}^{2}, K = 1, 2, 3, . . . .$ se llama espectro de potencias y representa la distribución de la potencia media por frecuencias.

Para la transformada integral de Fourier el teorema de Parseval se representa con la igualdad

(14) \int_{- \infty}^{\infty} x^{2} (t) d t = \frac{1}{2 π} \int_{- \infty}^{\infty} {|C^{*} (ω)|}^{2} d ω

cuya parte izquierda representa la energía del proceso y la igualdad puede escribirse en la forma

d E = {|C^{*} (ω)|}^{2} d ω \Rightarrow {|C^{*} (ω)|}^{2} = \frac{d E}{d ω}

Entonces, en diferencia de los coeficientes del espectro discreto, el cuadrado del módulo de la densidad espectral compleja representa la distribución de la energía de la señal en frecuencias.

La transformación estructural de las señales vibratorias se ejerce a través de funciones ortogonales que son más cómodas. Con el desarrollo de los sistemas computacionales rápidos y con aumento de sus memorias se ha desarrollado el algoritmo computacional Transformada Rápida de Fourier $(F F T)$ .

Análisis de señales estocásticas

Las vibraciones son muy comunes en la naturaleza y se pueden caracterizar como procesos vibratorios donde un objeto siente movimientos irregulares en ciclos que no se repiten exactamente. En la gran mayoría de los sistemas reales las señales están acompañadas de efectos aleatorios relacionados con las características del medio que los rodea. Este grupo de señales son del grupo de señales no determinísticas o aleatorias. La información no necesaria, que contienen ellos se separa a través de transformaciones estadísticas y estructurales.

La pertenencia de las magnitudes aleatorias que determinan el estado vibratorio de las máquinas rotatorias a las que tienen distribución normal se define a través del teorema del límite central, el cual dice que la suma de una cantidad grande de eventos linealmente independientes tiene una distribución de probabilidad cerca de la normal. Las señales que definen el estado vibratorio de las máquinas rotatorias son resultado de superposición de gran cantidad de acciones dinámicas y responden a las condiciones del teorema de límite central (teorema de Lapunov).

Para poder describir una vibración aleatoria, teóricamente se necesitará un espacio de tiempo observable infinito que es imposible (solo tiempos finitos se utilizan). Así mismo, si el tiempo observado es muy largo será un modo de descripción muy inconveniente. Por esto se han creado métodos comúnmente utilizados. Estos métodos tienen su origen en la mecánica estadística y teoría de comunicaciones que utilizan conceptos como distribución de probabilidad, densidades y espectro de frecuencias.

Las señales aleatorias no pueden ser descritas por una expresión matemática explícita como las señales determinísticas y deben ser estudiadas a partir de criterios estadísticos por el gran número de posibles formas de respuestas que tienen los sistemas dinámicos reales como reflejo de las diferentes acciones de excitación sobre ellos. En la dependencia de cómo sea la respuesta del sistema aleatorio estos pueden emitir señales aleatorias estacionarias (cuando sus características estadísticas no dependen del tiempo $X (t) = const, σ_{x} (t) = const$ y la función de autocorrelación no depende del tiempo inicial, depende solamente de la diferencia entre dos momentos de tiempo $τ$ ) o no estacionarias (véase figura 2). Esto permite en la práctica usar una sola función fundamental (muestra) del proceso aleatorio, la cual será estacionaria si las propiedades que se calculan en un intervalo de tiempo dado no varían notablemente respecto a otro intervalo de tiempo próximo. Además las señales estacionarias se pueden dividir en ergódicas y no ergódicas. Las ergódicas son aquellas cuyas características estadísticas coinciden promediándolas. De lo contrario son denominados no ergódicas. Esta clasificación es de gran importancia práctica ya que permite calcular las propiedades de un fenómeno mediante el estudio de una sola muestra.

Las técnicas de análisis estocástico se dividen en dos tipos: las basadas en el dominio del tiempo y las que se basan en el dominio del la frecuencia.

La modelización de los procesos estocásticos en el dominio del tiempo se apoya en el cálculo de los coeficientes de autocovarianza y autocorrelación, que se expresan en función del “retardo” o distancia en el conjunto índice de separación entre observaciones estudiadas.

Los estudios en el dominio del tiempo se encuentran con el problema de que en dos dimensiones no existe una única definición de distancia, por lo que el fenómeno del retardo y la ordenación de éste provocan una complejidad muy elevada.

Dadas las dificultades para describir completamente procesos espaciales a partir de las técnicas en el dominio del tiempo, el análisis espectral ofrece un procedimiento de análisis espacial diferente. La aplicación de este tipo de análisis permite la modelización espacial de la distribución de la variable por medio de la “función de densidad espectral”, y la cuantificación de la correlación espacial entre variables por medio de la “coherencia espectral”. Se aplica la Transformada de Fourier para pasar al dominio de la frecuencia (cambio de sistema de referencia), donde el fenómeno de retardo y la adopción de indicadores para definir la dependencia entre observaciones, pierde su importancia. En este dominio, la modelización para describir las variaciones espaciales, se simplifica notablemente y permite la descripción de modelos que recogen toda la variabilidad del sistema a partir de un conjunto finito de ondas elementales.

Cuando los procesos aleatorios son estacionarios y ergódicos se usan cuatro funciones estadísticas importantes:

Valor medio cuadrático
Función de densidad de probabilidad
Función de correlación
Función de densidad de potencia espectral

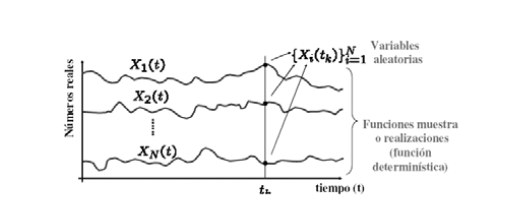
Si estudiamos las señales vibratorias en n puntos de un objeto o de n objetos en el mismo punto, recibiremos un conjunto de curvas dependientes del tiempo $X (t), i = 1, 2, . . . ., n$ .

Para el conjunto de señales vibratorias, compuesto por los eventos elementales $X = x_{i} (t_{j}), i = 1, 2, . . . ., n$ , cuales se presentan o no en el momento $t = t_{j}, j = 1, 2, 3, . . ., m,$ el valor medio cuadrático da la energía con que es emitida la señal y puede ser determinada promediando los valores cuadráticos de cada punto de la muestra en un intervalo de tiempo definido, el cual se puede determinar mediante la siguiente ecuación:

(15) \bar{x^{2}} = \lim_{T \to \infty} \frac{1}{2 T} \int_{- T}^{T} x^{2} (t) d t

El valor medio o componente estática de la señal aleatoria puede ser expresada mediante el valor medio estadístico como:

(16) u_{x} = \lim_{T \to \infty} \frac{1}{2 T} \int_{- T}^{T} x (t) d t

Para caracterizar la amplitud de la distribución de los valores instantáneos de la señal aleatoria descrita por la función alrededor de su valor medio, se define otro término estadístico, la varianza:

(17) V a r = \frac{1}{T} \int_{0}^{T} {(x (t) - u_{x})}^{2} d t

que es igual al cuadrado de la desviación estándar, la cual representa la medida de la distribución de los valores instantáneos alrededor del valor medio:

(18) σ_{x}^{2} = V a r = x^{2} - u_{x}^{2}

Si la componente estática de la señal es cero, entonces la desviación estándar será solo función de los valores cuadráticos de la señal recibiendo el nombre de Raíz Media Cuadrática $(RMS)$ que es una medida muy utilizada para determinar el comportamiento dinámico de un sistema.

(19) σ_{x}^{} = \sqrt{\frac{1}{T} \int_{0}^{T} x^{2} (t) d t} = \sqrt{x^{2}}

Así, para un intervalo de tiempo de medición $T$ el valor $R M S$ reflejará la energía que es liberada por la oscilación como función de su amplitud.

En el estudio de procesos continuos, como son vibraciones aleatorias estacionarias, es conveniente tratar el concepto de densidad probabilística en lugar de probabilidad sencillamente. La densidad probabilística se define como la probabilidad de encontrar valores de amplitudes instantáneas dentro de un intervalo de amplitud, $Δx$ , dividido por el tamaño del intervalo, consiguiendo así densidad. Normalmente la probabilidad no tiene dimensión, pero la densidad probabilística sí tiene una forma de dimensión.

Matemáticamente formulada, la densidad probabilística a un nivel de amplitud especificado, $x$ , es:

$p (x) = \lim_{Δ x \to 0} \frac{p (x) - p (x + Δx)}{Δx}$

Aquí $p (x)$ es la densidad probabilística y $p (x)$ es la probabilidad de que cualquier amplitud instantánea exceda el valor $x$ y $p (x + Δx)$ es la probabilidad de ocurrencia de que los valores de amplitudes instantáneas excedan el nivel $x + Δx$ . Si graficamos el valor $p (x)$ para todos los valores de $x$ , se puede obtener una curva de densidad probabilística que tiene la característica de que su integración desde un valor $x 1 a x 2$ dará inmediatamente la probabilidad de ocurrencia de amplitud instantánea de valores en dicho intervalo $(x 1 - x 2)$ , independientemente de la magnitud de $x 1 y x 2$ . Es una ventaja presentar datos probabilísticas en forma de densidad probabilística porque permite comparar directamente los datos entre experimentos independientemente del tamaño del intervalo de la amplitud, $Δx$ , utilizado en el experimento. Como normalmente se presentan datos probabilísticos en forma de curvas de densidad probabilística entonces esta forma de presentar datos es considerada la aceptada.

Aunque la densidad probabilística sea una descripción de señal muy útil y muestra excelente información sobre cómo las amplitudes instantáneas son distribuidas en una señal vibratoria, no muestra información sobre el contenido de frecuencias del proceso estudiado. Para obtener más información descriptiva, los físicos estadísticos introdujeron una función llamada la función de autocorrelación, $Rxx (τ)$ . Esta función describe como un valor de amplitud instantánea en particular depende de otros valores instantáneos y se define como:

(20) R_{x x} (τ) = \lim_{T \to \infty} \frac{1}{2 T} \int_{- T}^{T} x (t) x (t + τ) d t

donde $X (t)$ es la magnitud del proceso vibratorio en un momento instantáneo arbitrario, $t y X (t + τ)$ es la magnitud del mismo proceso observado un tiempo después, $τ$ .

Un proceso físico puede representarse en el dominio del tiempo $X (t)$ o en el dominio de la frecuencia $X (w)$ . Existe una relación directa entre ambas representaciones a través de la transformada de Fourier y su inversa:

(21) x (t) = \frac{1}{2 π} \int_{- \infty}^{\infty} X (i ω) e^{i n ω t} d ω, X (i n ω) = \frac{2}{T} \int_{- \infty}^{\infty} x (τ) e^{i ω τ} d t

Determinamos la función $X (t + τ)$

(22) x (t + τ) = \frac{1}{2 ω} \int_{- \infty}^{\infty} X (i ω) e^{i ω (l + τ)} d ω

Y obtenemos la función de autocorrelación:

(23) R_{x x} (τ) = \lim_{T \to \infty} \frac{1}{2 ω} \int_{- \infty}^{\infty} x (t) \frac{1}{2 π} \int_{- \infty}^{\infty} X (i ω) e^{i ω t} e^{i ω t} d ω d t = \frac{1}{2 π} \int_{- \infty}^{\infty} \lim_{T \to \infty} \frac{1}{2 T} (\int_{- T}^{T} x (τ) e^{i ω τ} d t) X (i ω) e^{i ω t} d ω = \frac{1}{2 π} \int_{- \infty}^{\infty} \lim_{T \to \infty} \frac{1}{2 T} X (- i ω) X (i ω) e^{i ω t} d ω

En un caso de un proceso estacionario aleatorio (ideal), la función de autocorrelación consistirá en una infinita función ‐ impulso cerca de cero $τ = 0$ (véase figura 5a). Como en cada proceso el valor de cada amplitud instantánea será completamente independiente de todos los otros valores de amplitudes instantáneas.

De igual manera, en la práctica, las funciones de autocorrelación están asociadas con un grupo de vibraciones alrededor de $τ = 0$ , pero nunca son cerca de infinita, impulso ‐ función, (figura 5b y 5c). La razón de esta separación de la curva alrededor de cero es que todos los procesos aleatorios son frecuentemente limitados, y mientras mas estrechas sean los limites de la frecuencia, más se separan hacia fuera las funciones de autocorrelación correspondientes.

La otra función muy importante en la práctica, es la llamada función de la raíz media de la densidad espectral. (función de densidad de potencia espectral) y puede ser derivada de la función de autocorrelación como sigue

(24) S_{x x} (ω) = \int_{- \infty}^{\infty} R_{x x} (ω) e^{- i ω τ} d τ

Por lo tanto, la densidad espectral de las señales estocásticas es la transformada de Fourier de la función de autocorrelación.

De esta relación surgen dos conclusiones sustanciales:

• $S_{xx} (w)$ no es una función aleatoria por que está recibida a través de $R_{xx} (τ)$ la cual no es una función numérica aleatoria.

• $S_{xx} (w)$ es una función real por que $R_{xx} (τ)$ es par y la parte imaginaria de $S_{xx} (w)$ es nula:

(25) i \int_{- \infty}^{\infty} R_{xx} (τ) s e n (ωτ) dτ = 0;

(26) S_{x x} (ω) {= \int}_{- \infty}^{\infty} R_{x x} (τ) \cos (ω τ) d τ

Las frecuencias negativas no tienen sentido físico y por esto se usa la densidad espectral:

(27) S_{x x} (ω) {= 2 \int}_{- \infty}^{\infty} R_{x x} (τ) \cos (ω τ) d τ, c o n ω > 0

De la teoría de integrales de Fourier es además conocido que $R_{x x} (τ)$ puede también encontrarse como:

(28) R_{x x} (τ) = \frac{1}{π} \int_{0}^{\infty} S_{x x} (ω) e^{- i ω τ} d ω, c o n ω > 0

La relación entre la función de autocorrelación $R_{x x} (τ)$ y la densidad espectral del proceso estocástico $S_{xx} (w)$ es a menudo llamada relación de Wiener – Khinchin y juega un papel muy importante en la teoría de los procesos aleatorios.

El sentido físico de la densidad espectral se recibe de la expresión de la potencia media del proceso (12) y usando el teorema de Parseval para el espectro complejo (14) se recibe:

(29) p = \frac{1}{2 π} \int_{- \infty}^{\infty} S_{x x} (ω) d ω

Podemos también escribir esta expresión en la forma $d P = \frac{1}{2 π} S_{x x} (ω) d ω$ y de donde recibimos:

(30) d P = \frac{1}{2 π} S_{x x} (ω) = \frac{1}{2 π} \frac{d P}{d ω}

Por lo tanto, la densidad espectral de la señal estocástica caracteriza la distribución de la potencia de la señal por la frecuencia.

Para la valoración de las relaciones conjuntas entre las componentes estructurales, recibidas en resultado de la transformación estructural de dos señales estocásticas $X (t) y y (t)$ , se usa la densidad espectral conjunta, la cual no tiene sentido físico y se define por:

(31) se pue S_{x y}^{*} (ω) = \lim_{T \to \infty} \frac{1}{T} C_{x}^{*} (i ω) C_{y}^{*} (- i ω)

transformada de Fourier de la función de correlación conjunta:

(32) S_{x y}^{*} (ω) = \int_{- \infty}^{\infty} R_{x y} (τ) e^{- i ω τ} d τ

También es válida la relación inversa:

(32) R_{x y} (τ) = \frac{1}{2 π} \int_{- \infty}^{\infty} S_{x y}^{*} (ω) e^{- i ω τ} d ω

De la última relación se puede concluir que si los procesos estocásticos son estadísticamente independientes $(R_{x y} (τ) = 0)$ la densidad espectral conjunta debe ser igual a cero para cualquier valor de ω.

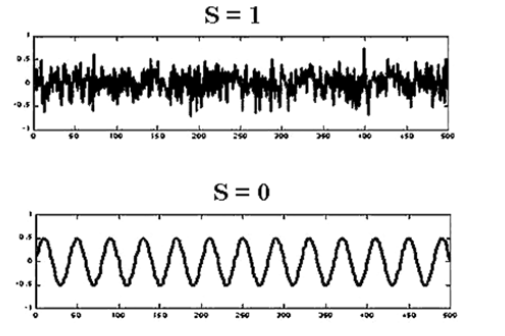
La transformación de los señales estocásticas se hace por descomposición en series de funciones ortogonales evaluando la entropía de las señales. La entropía puede ser entendida como un concepto físico que se relaciona con el grado de desorden de un sistema. En análisis de señales la entropía cuantifica el grado de irregularidad presente en la señal. En un ejemplo simple si una señal es perfectamente regular o predecible, su entropía es mínima. En caso opuesto, si la señal es extremadamente compleja, irregular o impredecible, su entropía es máxima (figura 6).

Teóricamente todo tipo de vibración estocástica que se encuentra en la práctica es no estacionaria porque sus propiedades estadísticas varían con el tiempo. Sin embargo, desde el punto de vista ingenieril, esta variación es tan lenta que muchas veces se puede considerar como estacionaria en sentido práctico.

Vibraciones estocásticas no estacionarias podrán en la práctica ser descritos como vibraciones estocásticas cuyas propiedades estadísticas cambian con el tiempo dentro de intervalos de tiempo, esenciales para la descripción. Para analizar y describir tales datos vibratorios es necesario tomar en cuenta su variación en propiedades estadísticas en el tiempo. Para analizar teóricamente y adecuadamente las vibraciones aleatorias no estacionarias se introduce el concepto de media de ensamble.

Como conclusión podemos mencionar algunas de las técnicas de análisis de señales vibratorias que existen y usan las análisis de señales arriba descritos:

El análisis frecuencial o espectral es la técnica más comúnmente empleada para el diagnóstico de fallas. Utilizando esta técnica se pueden identificar fallas típicas. La idea fundamental del análisis frecuencial es encontrar la relación existente entre la frecuencia de las componentes discretas presentes en el espectro y la frecuencia de las fuerzas dinámicas que generan las vibraciones.
El análisis de la forma de onda o de la vibración en el dominio tiempo consiste en extraer información útil para el diagnóstico del gráfico de la amplitud vibratoria versus el tiempo. Resulta ser de gran utilidad cuando para fallas diferentes los espectros son similares.
El análisis de fase es el estudio de la diferencia de tiempo en que suceden dos eventos relacionados entre sí. Su análisis permite, por ejemplo, conocer la forma de deflexión en operación de una estructura.
El análisis de órbitas consiste principalmente en analizar la gráfica de la amplitud de la vibración horizontal $X (t)$ en función de la vertical $y (t)$ , para una sola frecuencia a la vez.
El análisis de coherencia permite relacionar causa – efecto entre dos señales vibratorias, estimando la relación lineal que existe entre dos señales vibratorias. Se define la función de coherencia ordinaria, y ${y^{2}}_{xy} (f)$ entre dos señales $x (t) y y (t)$ . $s í {y^{2}}_{xy} (f) = 1.0,$ las señales son perfectamente coherentes y sí ${y^{2}}_{xy} (f) = 0$ , las señales son incoherentes, es decir, no existe ninguna relación causa ‐ efecto entre ellas.
Otras técnicas utilizadas para el análisis de vibraciones son: promedios sincrónicos en el tiempo, demodulación o análisis de envolvente, análisis de transientes, análisis de partidas o paradas, análisis cepstrum, entre otras.

Bibliografía

1. Charles Ebeling. An Introduction to Reliability and Maintainability Engineering, Mc Graw-Hill 1997 ISBN: 0-07-0188521

2. Ireson, Coombs, Moss. Handbook of Reliability Engineering and Management, Second Edition Mc Graw-Hill 1996 ISBN: 0-07-012750-6

3. Rosaler, Robert C. (2002). Manual del Ingeniero de Planta. Mc GrawHill/Interamericana de Editores, S.A. de C.V.

4. Mosquera, Díaz, Cardona, Las vibraciones mecánicas y su aplicación al mantenimiento predictivo, Colección monográficas, Universidad Central de Venezuela, Instituto Superior de Ciencia y Tecnologías Nucleares de Cuba, ISBN: 980-00-1490-X.

5. A.M. Писарев, Механични трептения, Държавно издатеʌство “Техника”, София.

6. R.B. Randall, Frequency Analysis, Brüel & Kjær.

7. Thomson, W.T., Teoría de vibraciones: aplicaciones, Prentice – Hall Hisp.

8. Harris, Cyril M., Shock and vibration handbook, ed. Crede, Charles E.

9. Newland, D.E., An introduction to random vibrations and spectral analysis.