EL PUNTO DE INFLEXIÓN Y LA HERRAMIENTA PX-BEN PARA EL CÁLCULO EN LOSAS MACIZAS DE HORMIGÓN ARMADO.

Introducción

Las losas macizas de hormigón reforzado son conjuntos o unidades que se diseñan para la asimilación de esfuerzos en su superficie y se responsabilizan de trasmitirlos hasta las vigas de carga. Su condición mecánica de trabajo está condicionada por las dimensiónes de sus luces y por la relación entre ellas. Asumen las cargas en una o dos direcciones y siempre de forma perpendicular al eje de las vigas de sustentación.

Como las demás estructuras reforzadas, están integradas por dos componentes esenciales: el hormigón y el acero. La participación de estos materiales implica, de acuerdo a las características del proyecto, costos más o menos relevantes que pueden ser considerables y en ocasiones, dichos costos, resultan de manera imprevista. Una cuantía de costos con desperdicios considerables puede conducir a resultados negativos de no analizarlos óptimamente. 

El tipo, cantidad, distribución y espaciamiento del refuerzo son desarrollados de acuerdo a la solicitud determinada en cada caso. Se disponen atendiendo las especificaciones técnicas, las normas y reglamentos vigentes.

Para lograr tabular de forma organizada la cuantía de costos del acero en losas macizas se debe definir adecuadamente los criterios de borde, la condición de adyacencia, espesor, apoyos y recubrimientos en cada modelo y sobre todo el parámetro de referencia en el levantamiento del refuerzo en los apoyos. El proceso maneja variables como el diámetro del refuerzo y su longitud comercial y en términos concluyentes se afirma que el fin último es determinar las barras que arrojan, en función del esquema estructural, el menor desperdicio unitario.

Al momento de realizar un diseño para determinar el valor de un proyecto se debe enfocar una mayor atención hacia las partidas de hormigón reforzado. Los planos estructurales establecen la disposición y el detallado y es necesario que el analista de costos pueda planear adecuadamente su misión y concebir los fundamentos que rigen el diseño.

El acero estructural, definido en función de su esfuerzo unitario admisible, es el que asume tracción en las losas sometidas a flexión pura y las barras de acero adicionales, adecuadamente habilitadas, encaran los esfuerzos suplementarios originados por los componentes de cortantes en vigas y la propia losa. 

El refuerzo se trabaja encima del encofrado o falso piso antes de vaciar el concreto y para esto hay que observar las recomendaciones mínimas sobre el criterio de levantamiento de las barras en los apoyos. En lo adelante se plantea un algoritmo de estimación del punto de inflexión (PI) que indicará la zona más aproximada de ocurrencia del cambio de momento. Esto permitirá una disposición más correcta del refuerzo durante la ejecución y una efectiva estimación de la cuantía de costos de los proyectos.

Es importante significar que la práctica actual para la determinación del peso de las barras del refuerzo referido al volumen unitario de hormigón, en el caso que nos ocupa, se maneja con cálculos sencillos y de estimación directa sobre todo para evadir la complejidad y tediosidad de la optimización lo que advierte que algunos resultados podrían arrojar errores o desviaciones considerables en la estructuración económica del proyecto. 

Para contribuir con la simplificación de los análisis de costos de las losas macizas de hormigón armado, se presenta a continuación un programa que se ha nombrado PX-BEN y con el que se pretende conducir, dichos análisis, hacia una mayor exactitud.

Fundamento Estructural del PX-BEN

El PX-BEN es un programa, sustentado en el método simplificado de Marcus para el cálculo del punto de inflexión en losas macizas de hormigón con refuerzos en una o dos direcciones y apoyadas en sus bordes por vigas perimetrales, muros o una combinación de ambos. 

Se denomina PX-BEN por las siguientes razones: PX que significa ”punto de cruce” haciendo alusión al punto de inflexión y BEN que son las tres primeras letras del apellido del Ing. José BENJAMÍN, quien hizo suyo el compromiso de acompañarnos y colaborar con el desarrollo del tema para el estudio sobre la simplificación en la determinación de la cuantía de costos optimizada. Se crea con la finalidad de optimizar la ejecución y el detalle del refuerzo indicando con el cálculo una aproximación en la ubicación de los puntos de momentos nulos que sirven de guías para el levantamiento de las barras de acero.

El punto de inflexión se obtendrá a partir de la determinación del diagrama de momento de la losa en ambas direcciones, usando las ecuaciones de las vigas de un tramo para las diferentes condiciones de apoyo en similitud con los apoyos de la losa. La longitud para la determinación de los diferentes momentos se medirán siempre a partir del apoyo izquierdo en la dirección X, y a partir del apoyo inferior en la dirección Y. Estos momentos serán corregidos por ciertos coeficientes para adaptarlos al comportamiento estructural de las losas como son los coeficientes de corrección por rigidez a la torsión, los coeficientes de corrección por la no colocación del refuerzo de torsión con ángulos libres en sus apoyos y los coeficientes de distribución de cargas para el análisis en ambas direcciones.

Determinación de los Coeficientes de Distribución de las Cargas

El PX-BEN está basado en la consideración de franjas unitarias ortogonales en el centro de de un tramo de losa con carga uniformemente distribuida en la dirección de los ejes X, e Y. 

Se llamará W a la carga total factorizada actuante y Wx a la porción de la carga total actuante en la franja en la dirección X, y Wy a la porción de la carga total actuante en la franja en la dirección Y.

$\mathrm{W}= \mathrm{Wx} + \mathrm{Wy}.$

En el centro de la losa, con las mismas condiciones de apoyo en ambas direcciones, las franjas tendrán la misma deflexión.

Analizaremos el caso de una losa con apoyos articulados en sus cuatro bordes:

$∆\mathrm{x}=\mathrm{Cx} \mathrm{Wx} {\mathrm{Lx}}^{\wedge }4/384 \mathrm{E} \mathrm{Ix} ∆\mathrm{x}=\mathrm{deflexión} \mathrm{en} \mathrm{x} \mathrm{Cx}=5$

$∆\mathrm{y}=\mathrm{Cy} \mathrm{Wy} {\mathrm{Ly}}^{\wedge }4/384 \mathrm{E} \mathrm{Iy} ∆\mathrm{y}=\mathrm{deflexión} \mathrm{en} \mathrm{y} \mathrm{Cy}=5$

$∆\mathrm{x}=∆\mathrm{y}$

$\mathrm{Cx} \mathrm{Wx} {\mathrm{Lx}}^{\wedge }4=\mathrm{Cy} \mathrm{Wy} {\mathrm{Ly}}^{\wedge }4$

$\mathrm{Si} \mathrm{C}=\mathrm{Cy}/\mathrm{Cx} \mathrm{N}=\mathrm{Ly}/\mathrm{Lx} \mathrm{M}=\mathrm{N} \mathrm{si} \mathrm{Ly}<\mathrm{Lx} \mathrm{y} \mathrm{M}=1/\mathrm{N} \mathrm{si} \mathrm{Lx}<\mathrm{Ly} \mathrm{donde} \mathrm{M}=\mathrm{Lc}/\mathrm{LI}$

$\mathrm{\alpha }1=1/(1+\mathrm{C}*{\mathrm{M}}^{\wedge }4) \mathrm{\alpha }2=\mathrm{C}*{\mathrm{M}}^{\wedge }4/(1+\mathrm{C}*{\mathrm{M}}^{\wedge }4)$

$\mathrm{si} \mathrm{M}=\mathrm{N}$

$\mathrm{Wx}=\mathrm{\alpha }2*\mathrm{W} \mathrm{Wy}=\mathrm{\alpha }1*\mathrm{W}$

$\mathrm{Si} \mathrm{M}=1/\mathrm{N}$

$\mathrm{Wx}=\mathrm{\alpha }1*\mathrm{W} \mathrm{Wy}=\mathrm{\alpha }2*\mathrm{W}$

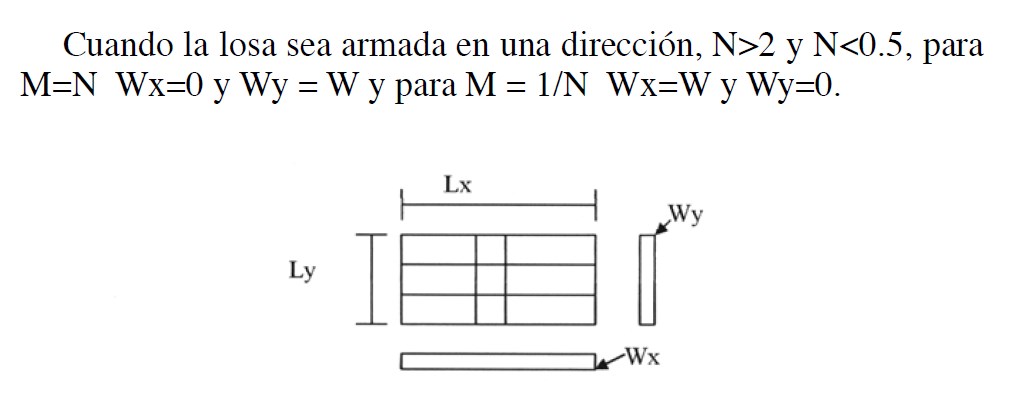
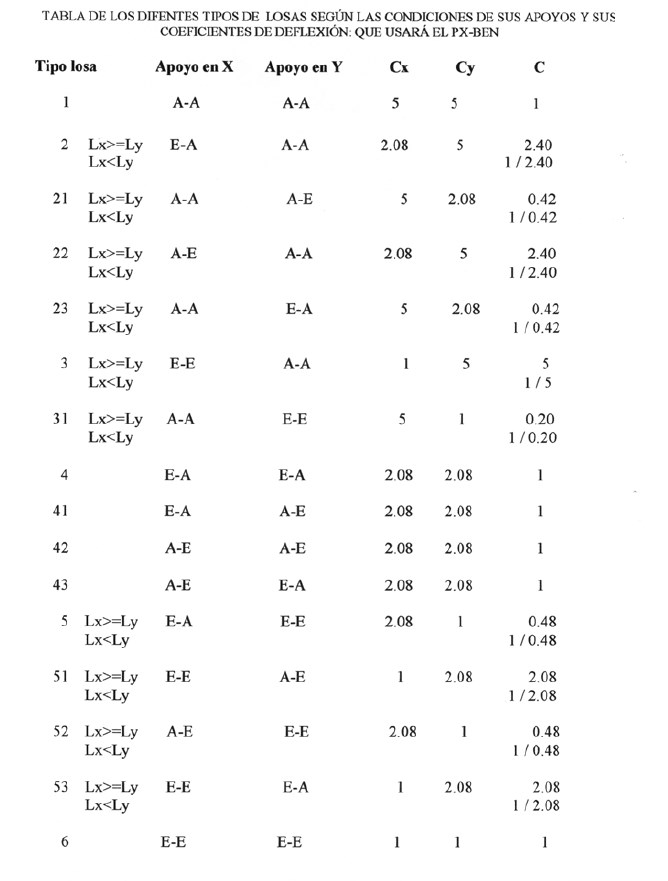
E = Apoyo empotrado, A = Apoyo articulado.

Las losas tipos 2, 21, 22, 23, 3, 31, 5, 51, 52, 53 con apoyos diferentes en ambas direcciones, tendrán un coeficiente C para $\mathrm{LX}>=\mathrm{Ly}$ igual $\mathrm{Cy}/\mathrm{Cx}$, y otro para $\mathrm{Lx}<\mathrm{Ly}$

Ecuaciones de los Momento en Vigas de un Tramo con Carga Uniformemente Distribuida

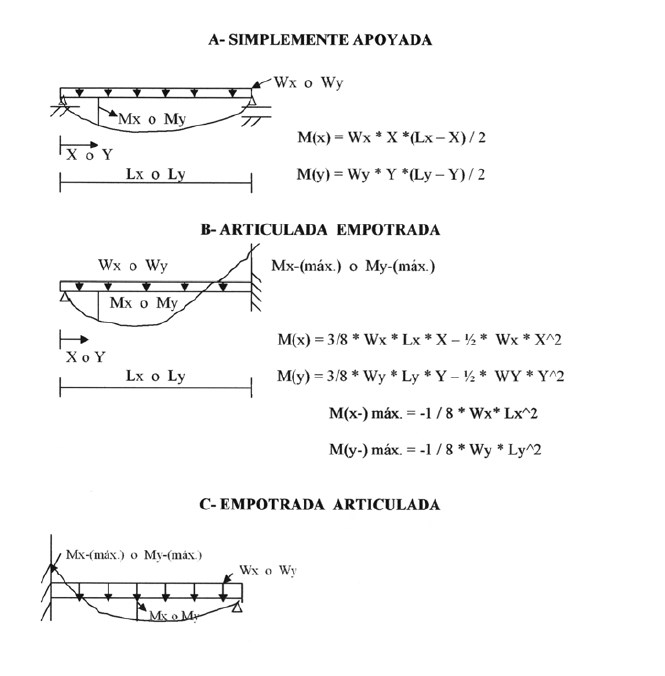
Determinación de los Coeficientes de Corrección por Torsión

Esta corrección se presenta en las losas que tienen ángulos libres en los que no se clocarán refuerzos de torsión y en los diferentes tipos de losas donde se considerará la rigidez a la torsión con coeficientes definidos por vx y vy. Los momentos del vano de las losas tipos 1,2,21,22,23,4,41,42 y 43 se corregirán con los coeficientes v’x y v’y.

Los coeficientes de corrección por rigidez a la torsión son:

$\mathbf{vx}=1-5/6* {\mathrm{Lx}}^{\wedge }2/ {\mathrm{Ly}}^{\wedge }2*8*\mathrm{MMx}/\left(\mathrm{W}*{\mathrm{Lx}}^{\wedge }2\right)$
$\mathbf{vy}=1-5/6* {\mathrm{Ly}}^{\wedge }2/ {\mathrm{Lx}}^{\wedge }2*8*\mathrm{MMy}/\left(\mathrm{W}*{\mathrm{Ly}}^{\wedge }2\right)$

Los momentos del vano serán afectados por estos coeficientes de la siguiente forma:

$$\begin{gathered} \mathrm{Mx}=\mathrm{vx}*\mathrm{MMx} \\ \mathrm{My}=\mathrm{vy}*\mathrm{MMy} \end{gathered}$$

Coeficientes de corrección para la no consideración de la armadura de torsión en las losas con ángulos libres:

$$\begin{gathered} \mathrm{v}\text{'}\mathrm{x}=\left(1+\mathrm{vx}\right)/2 \\ \mathrm{v}\text{'}\mathrm{y}=\left(1+\mathrm{vy}\right)/2 \end{gathered}$$

Los momentos de los vanos serán corregidos por dichos coeficientes como sigue:

$$\begin{gathered} \mathrm{Mx}=\mathrm{v}\text{'}\mathrm{x}*\mathrm{MMx} \\ \mathrm{My}=\mathrm{v}\text{'}\mathrm{y}*\mathrm{MMy} \end{gathered}$$

Los momentos considerados en los apoyos continuos son los momentos de empotramientos perfectos. En los apoyos discontinuos de las losas donde los puntos de inflexión, según la teoría elástica, están en dichos apoyos, el PX-BEN asume que los puntos de inflexión para estos casos están en Lx / 7 ó Ly / 7, según la dirección analizada, medido a partir de la cara interior del apoyo.

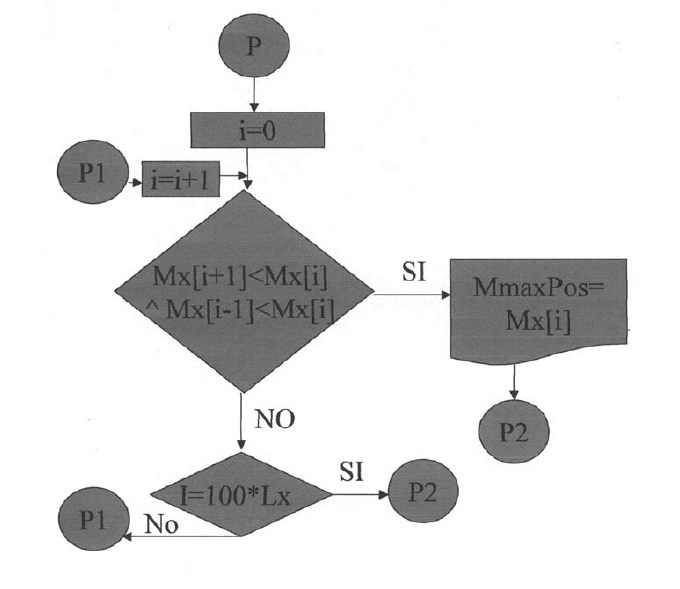
Diagrama de Flujo del PX-BEN

Plantillas desde la primera hasta la cuarta.

El programa inicia solicitando el número total de losas a analizarse y requiere el ingreso de los datos de cada una. Los datos requeridos son : Wi (carga total actuante en la losa), Lxi (longitud de la losa en la dirección X), Lyi (longitud de la losa en la dirección Y).

Una vez suministrado el conjunto de datos el programa, según el tipo de losa, asignará los coeficientes de deflexión correspondientes y calculará la relación entre las longitudes de las losas, $\mathrm{N} = \mathrm{Lyi} / \mathrm{Lxi}$ y $\mathrm{N} = \mathrm{Lyi} / \mathrm{Lxi}$, para fijar su condición de trabajo en una o dos direcciones (Para una dirección $\mathrm{N} > 2 \mathrm{ò} \mathrm{N}< 0.5$, para dos direcciones $0.5<= \mathrm{N}<=2)$. Esto es con la finalidad de determinar qué porción de la carga total le corresponderá a cada dirección de la losa.

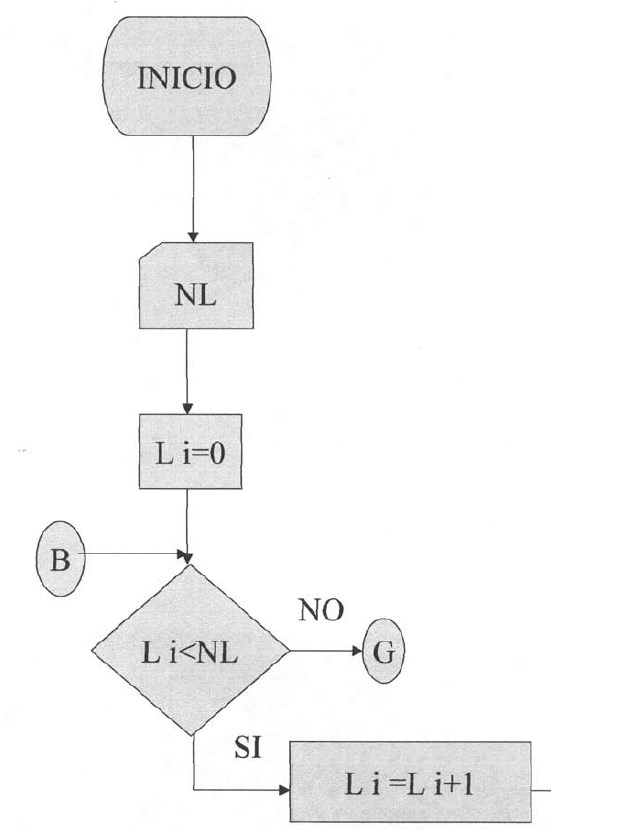
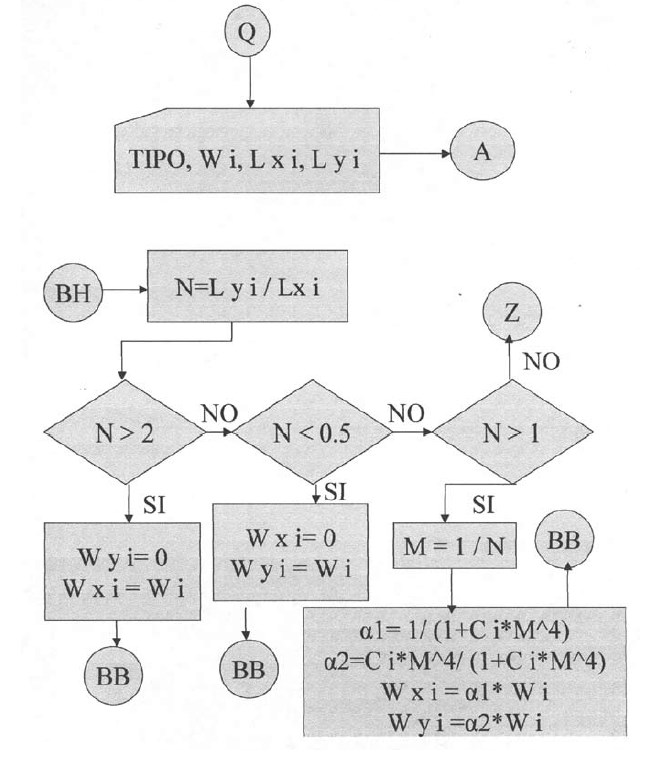
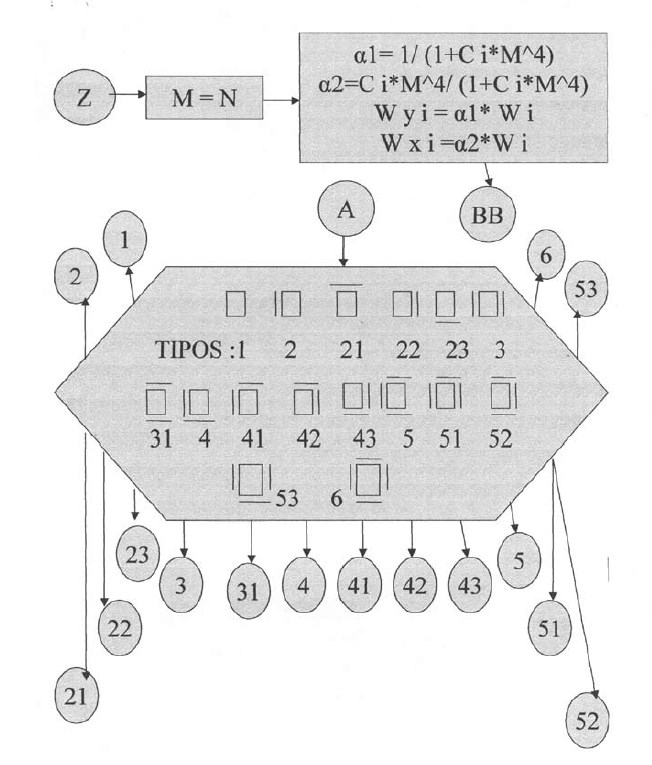
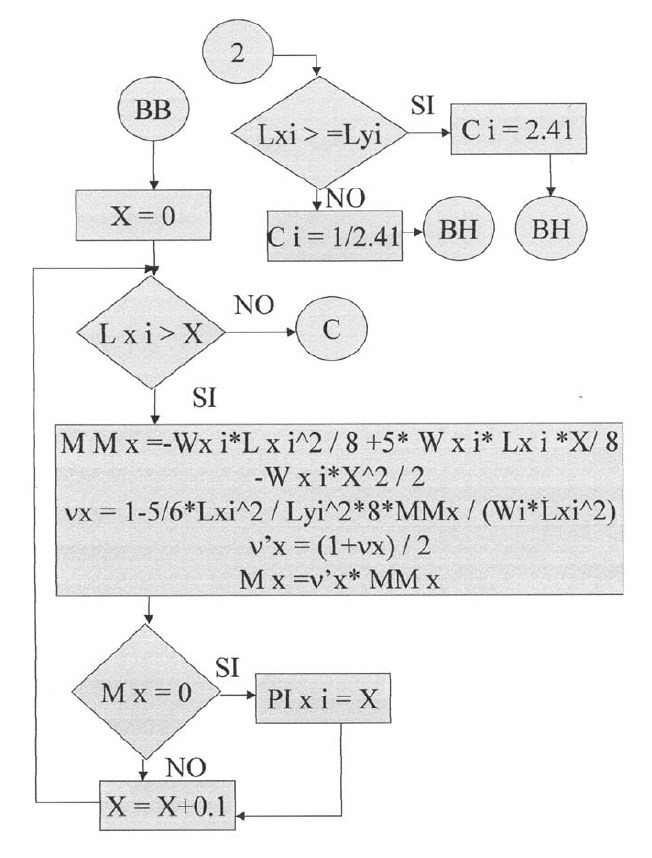
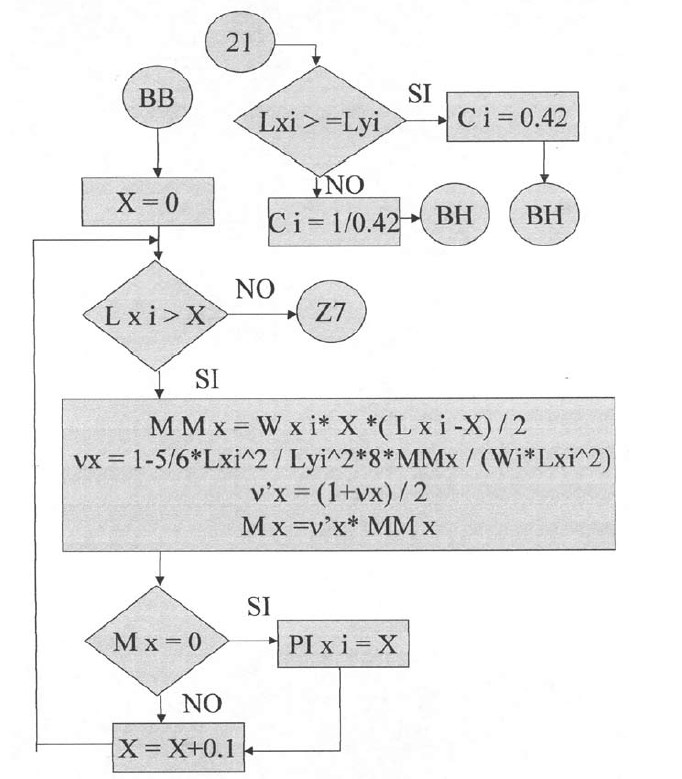
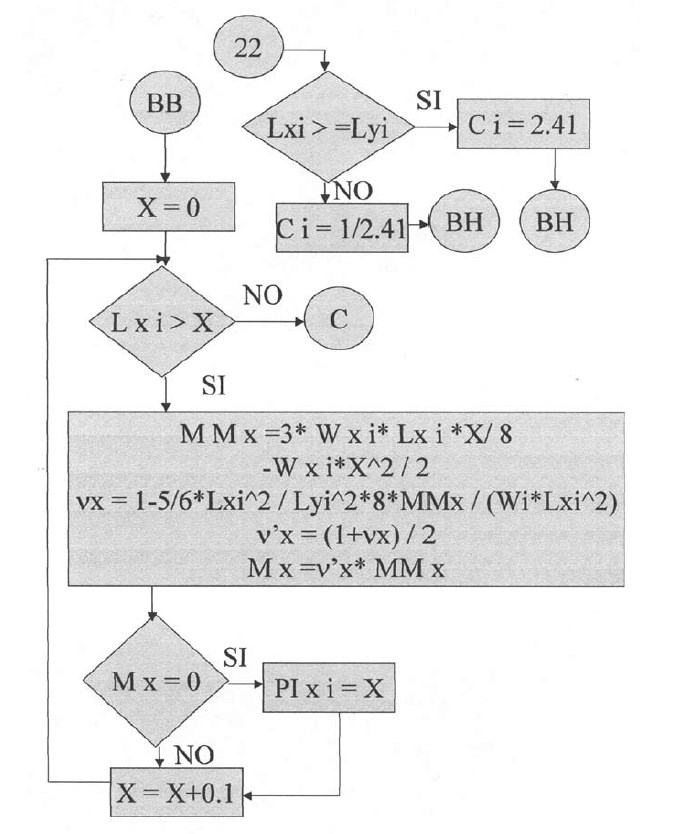
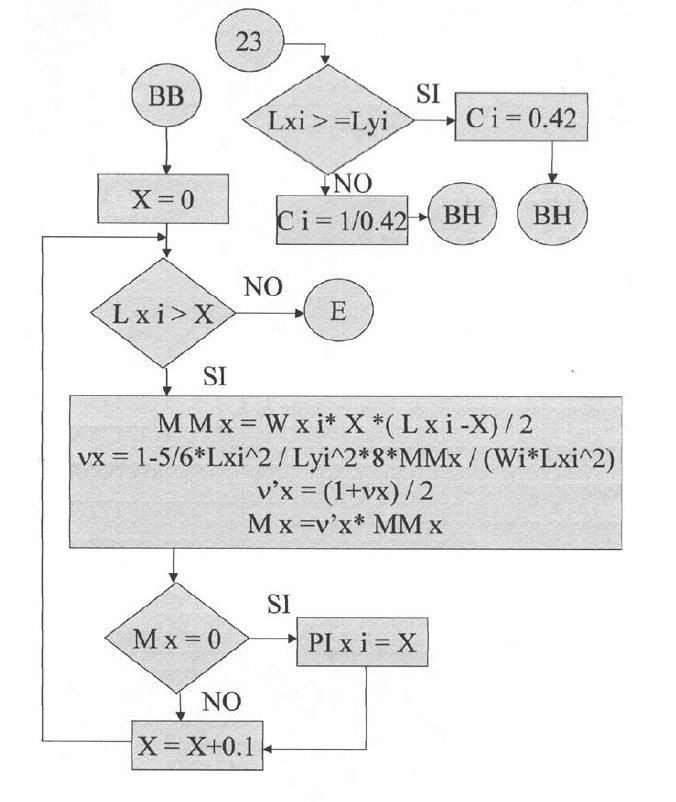
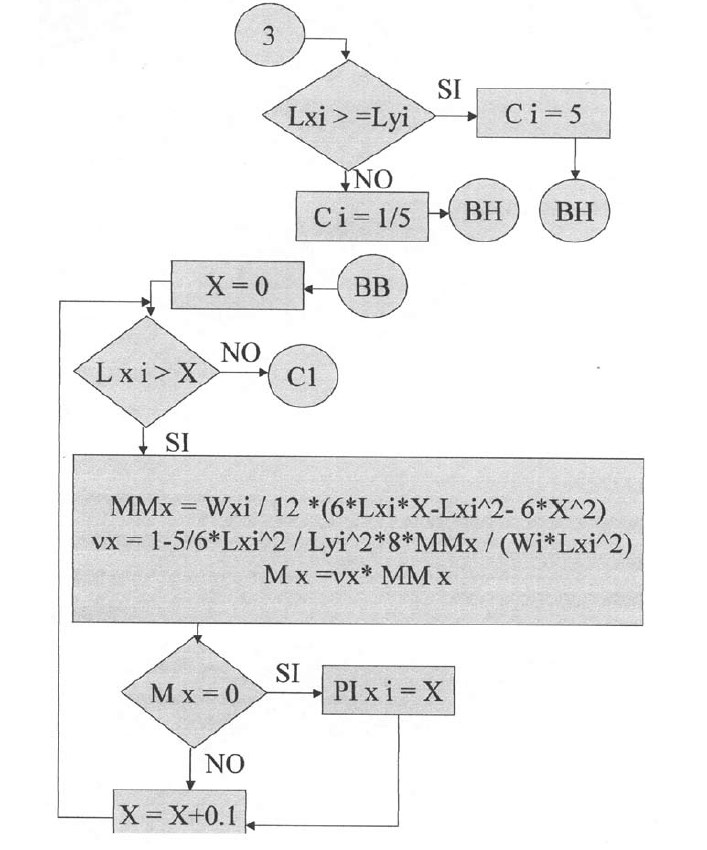
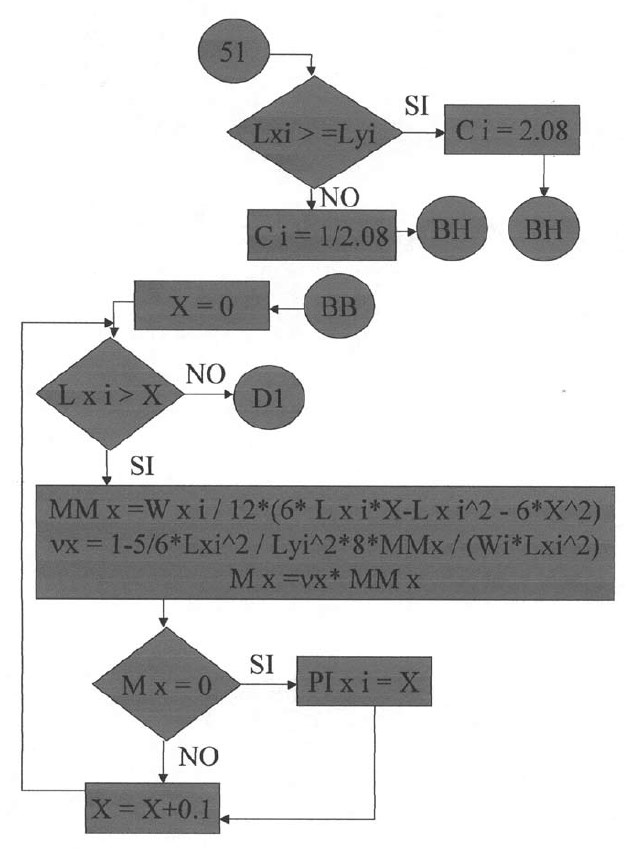
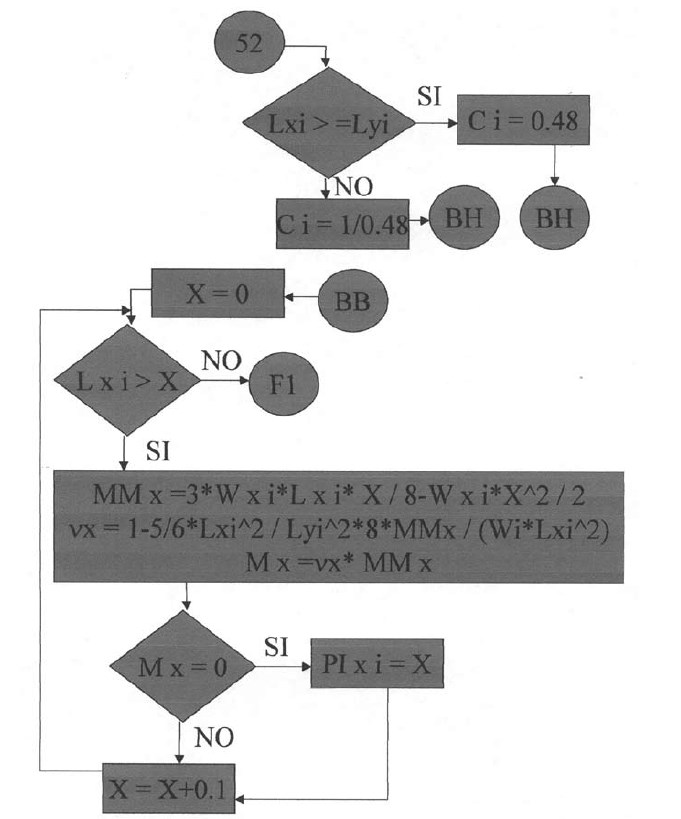
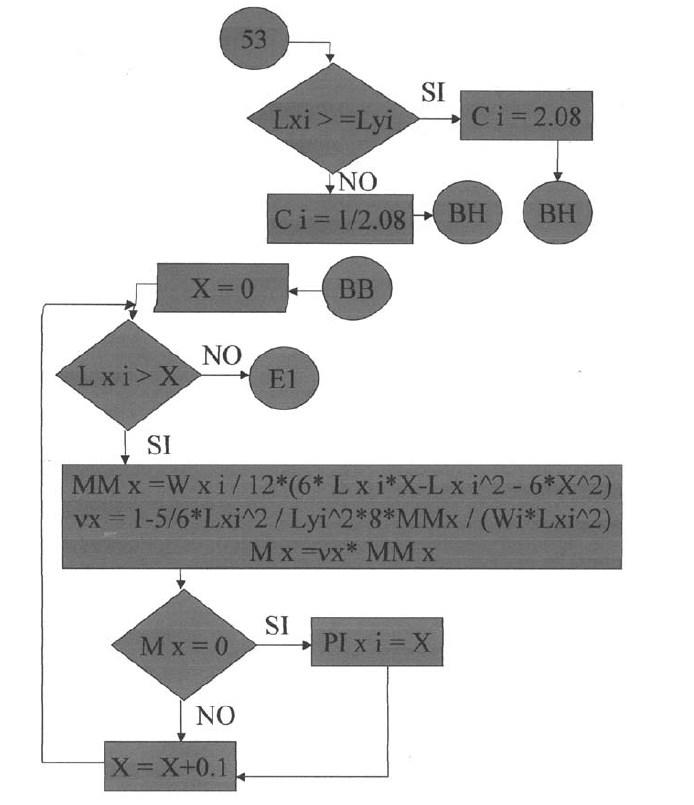
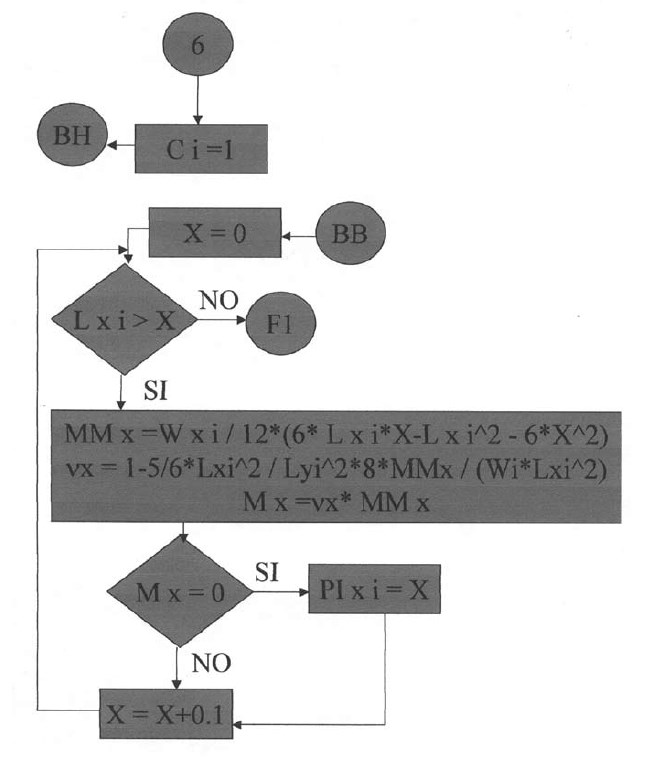
Plantillas desde la quinta hasta la vigésimo sexta.

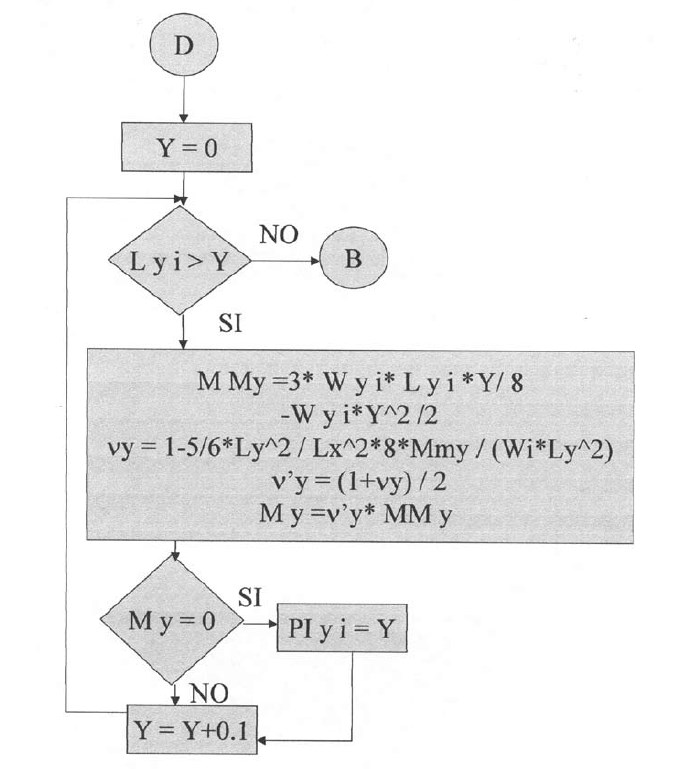
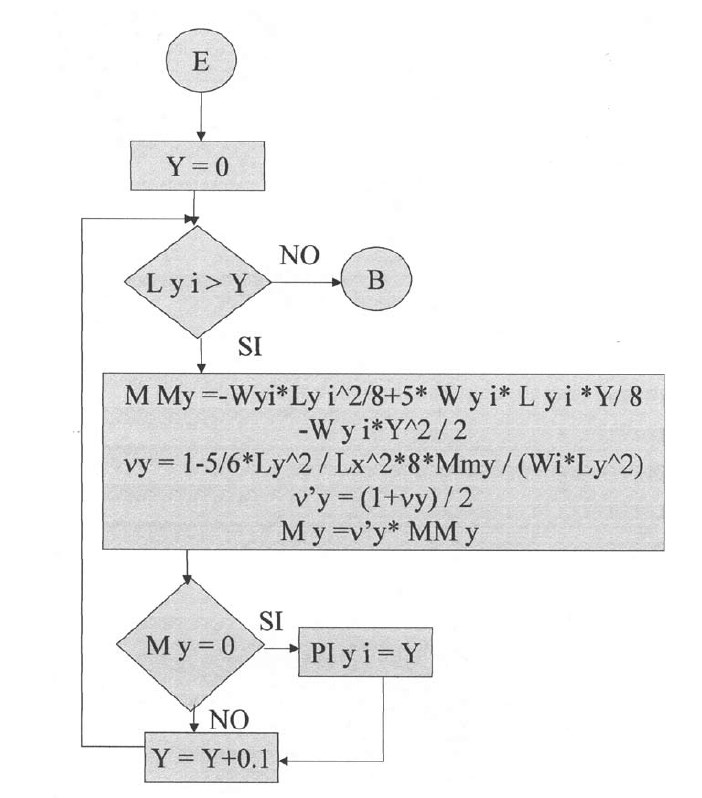
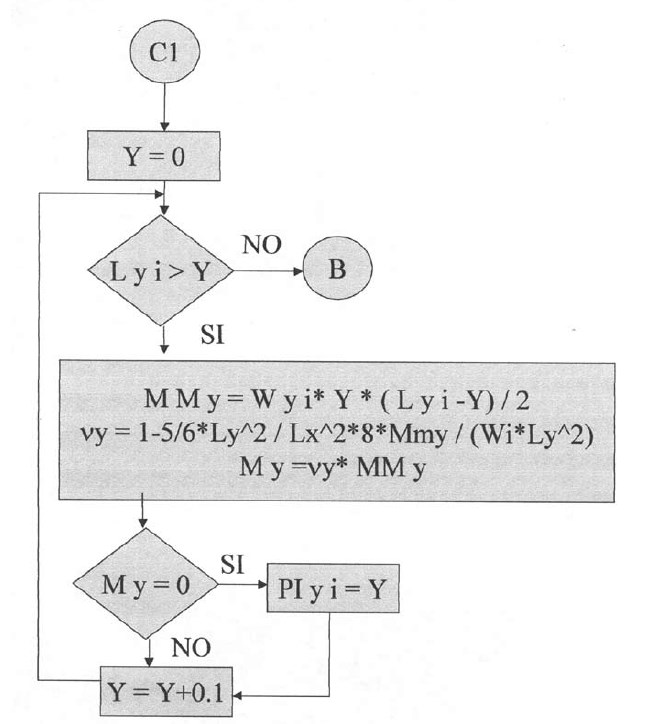
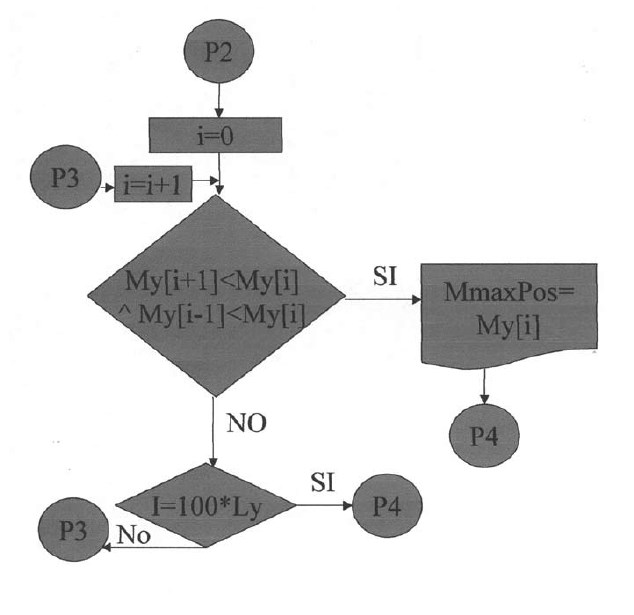
En las siguientes plantillas el programa calculará los momentos de todos los puntos en la dirección X, con una variación de 0.1 iniciando desde el apoyo izquierdo y considerando la rigidez a la torsión. Para la posición donde el momento es cero se tendrá el punto de inflexión para la dirección X. De igual manera se procederá para la determinación del punto de inflexión en la dirección Y.

Una vez calculado los puntos de inflexión en ambas direcciones el programa pasará a analizar la siguiente losa y así sucesivamente hasta analizarlas todas.

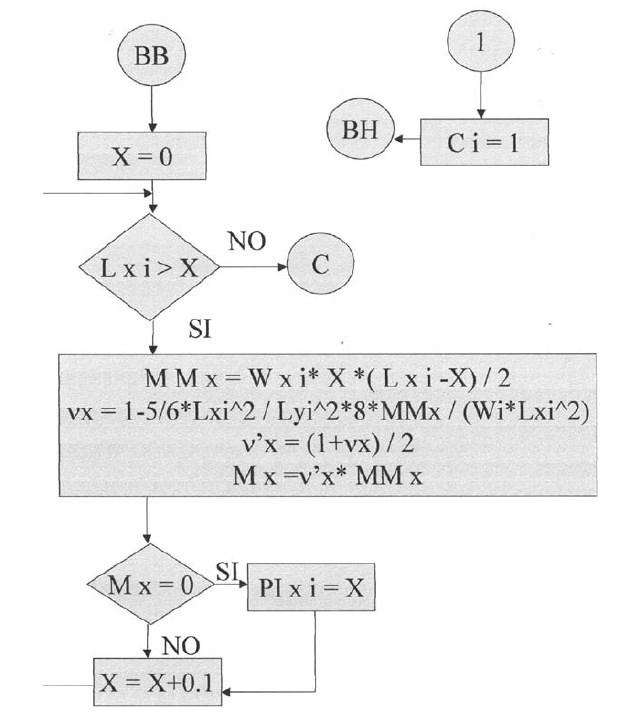
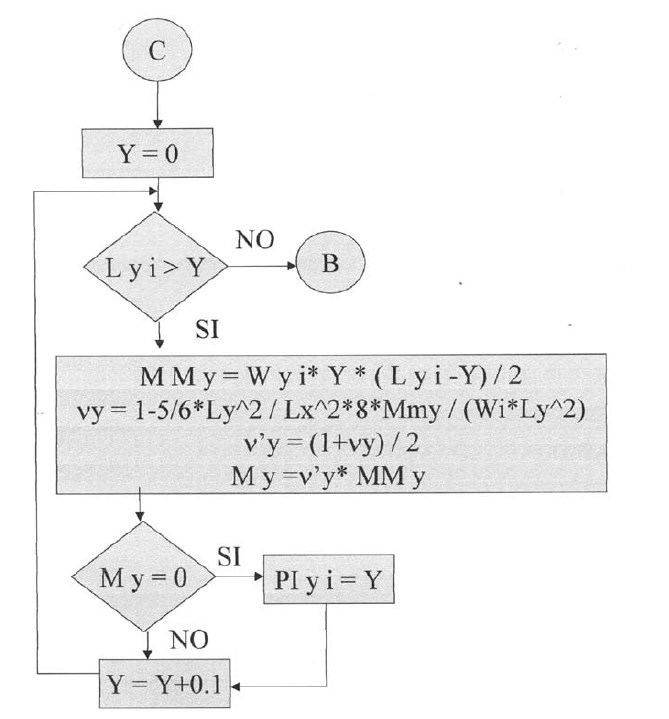
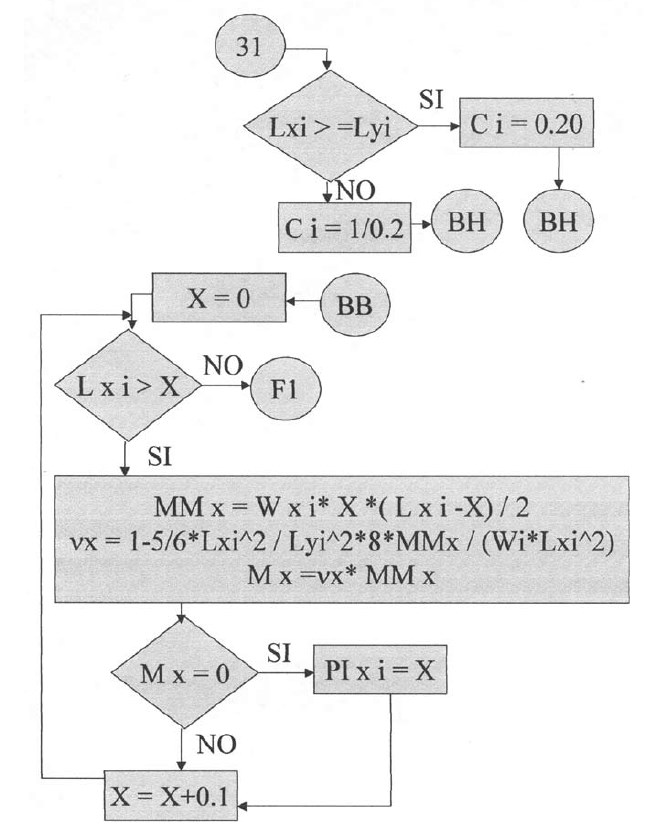
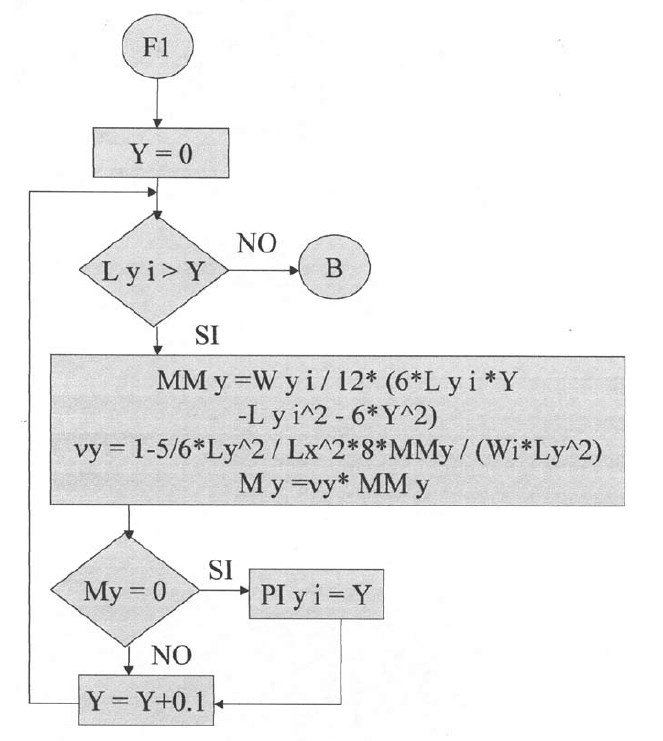
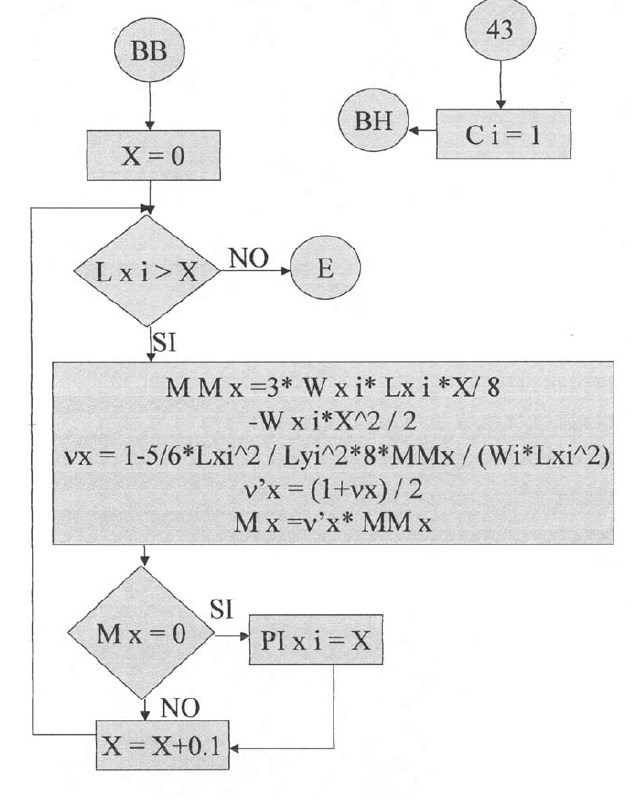
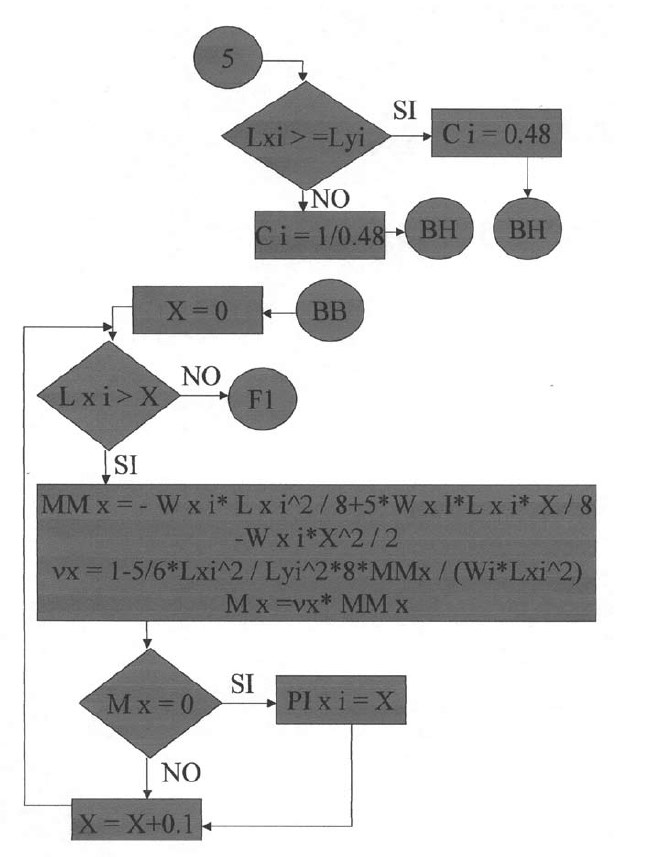
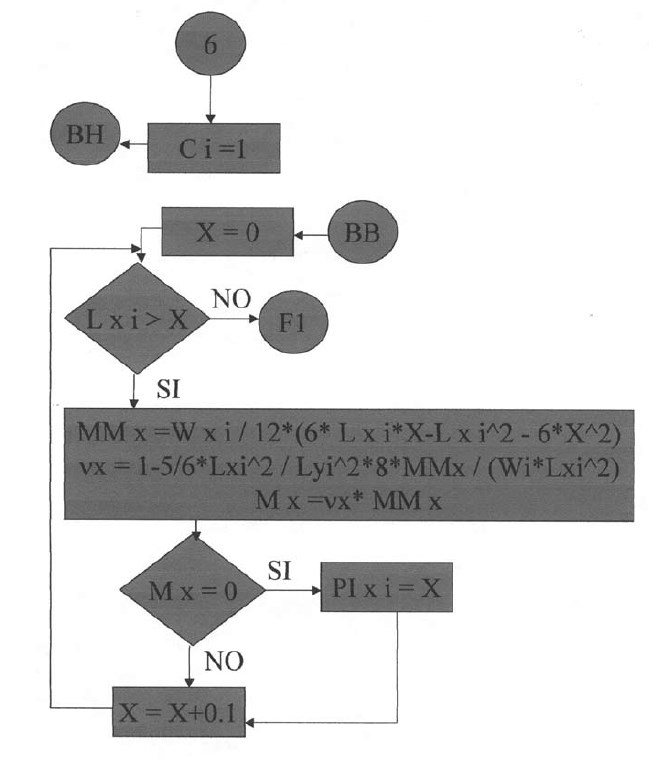
Plantillas vigésimo séptima y vigésimo octava.

A continuación el programa calculará los puntos de inflexión en las losas con apoyos discontinuos (articulados), que se encuentran en dichos apoyos. El programa asume que los puntos de inflexión, para estos casos, estarán en la dirección X, en Lx / 7 para el apoyo izquierdo y 6Lx / 7 para el apoyo derecho; y en la dirección Y, en Ly / 7 para el apoyo inferior y 6Ly / 7 para el apoyo superior.

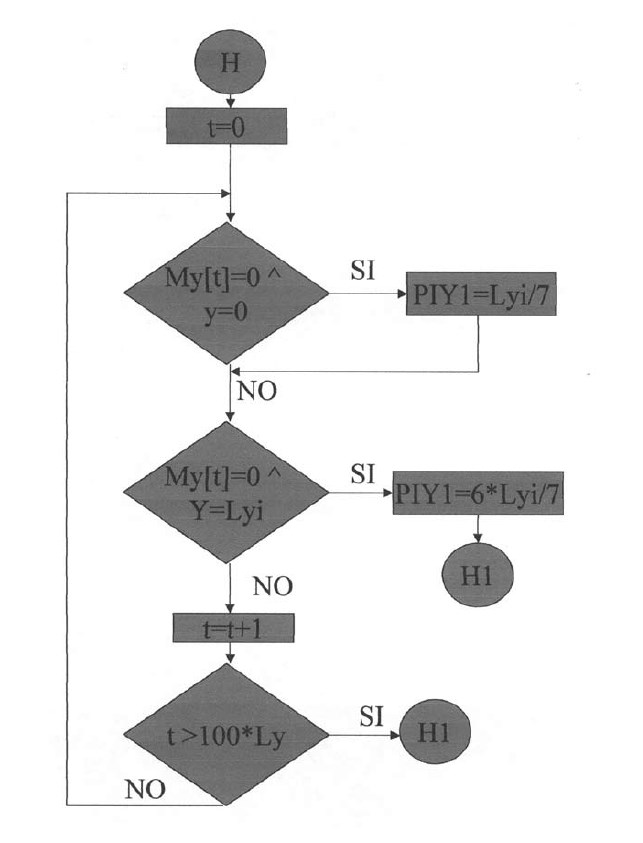
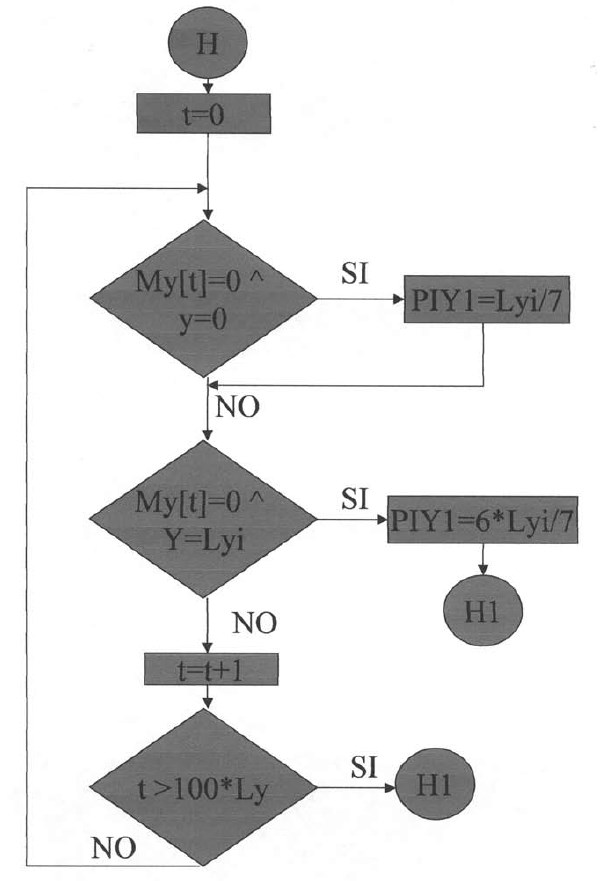
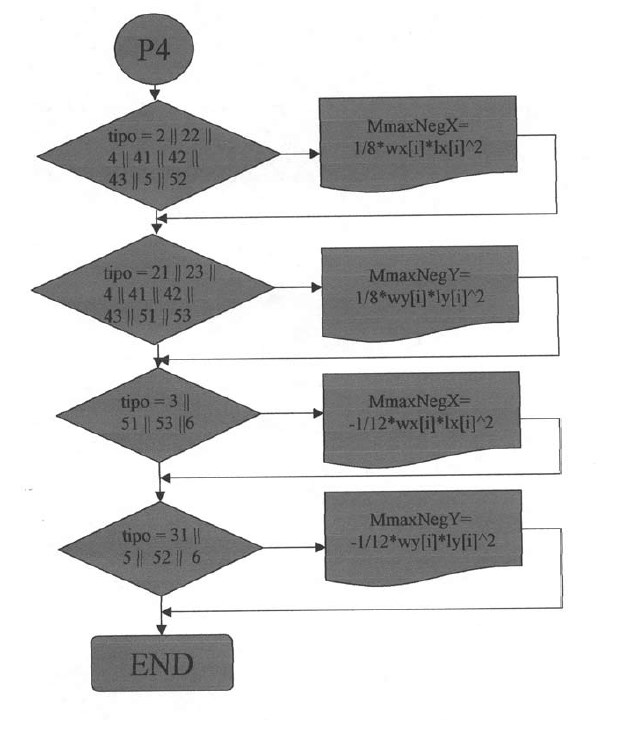
Plantillas desde la vigésimo novena hasta la trigésimo segunda.

En estas plantillas el programa presentará los resultados de los diferentes puntos de inflexión de las losas analizadas y mostrará los resultados del cálculo de los momentos máximos positivos y negativos.

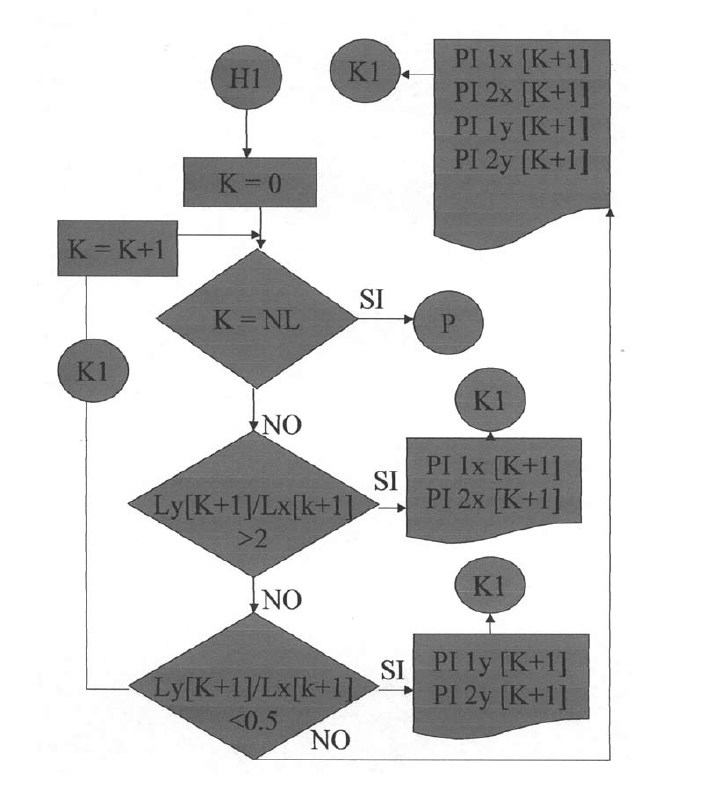
Bibliografía

AMBROSE, James.
PARKER, Harry.
2001,“Ingeniería Simplificada para Arquitectos y Constructores”
Editorial LIMUSA, S.A. de C.V., México, D.F.

IMCA, Instituto Mexicano de la Construcción en Acero, A.C.
2002,“Manual de Construcción en Acero-DEP: Diseño por Esfuerzos Permisibles”
Editorial LIMUSA, S.A. de C.V., México, D.F.

INSTITUTO MEXICANO DEL CEMENTO Y DEL CONCRETO, A.C.
1997,“Reglamento Para las Construcciones de Concreto Estructura y Comentarios”
ACI –318-95, ACI-318R-95

JIMENEZ, P.
GARCIA, A.
MORAN, F.
“Hormigón Armado”
13va Edición, Editorial GUSTAVO GILL, S.A.
Barcelona, ESPAÑA.

KASSIMALI, Aslam
1999,“Análisis Estructural”
Editorial THOMSON-LEARNING, México, D.F.

KIDDER, Frank E.
PARKER, Harry.
1993,“Manual del Arquitecto y Constructor”
Editorial LIMUSA, S.A. de C.V., México, D.F.

HIBBELER, Rusell
1997,“Análisis Estructural”
Tercera Edición, PEARSON EDUCACIÓN, México, D.F.

LOSER, Benno
“Hormigón Armado”
Editorial EL ATENEO, 8va. Edición

NILSON, Arthur H.
1999,“Diseño de Estructuras de Concreto”
Editorial McGRAW-HILL, Inc., México, D.F.

OLIN, Harold B.
SCHMIDT, John L. LEWIS, Walter H.
1995, “Construction, Principles, Materials and Methods”
Ediciones VAN NOSTRAND REINHOLD

PARK, R.
GAMBLE, W. L.
1995,“Losas de Concreto Reforzado”
Editorial LIMUSA, S.A. de C.V., México, D.F.

PARMLEY, Robert O.
1995,“Field Engineer’s Manual”
Editorial McGRAW-HILL, Inc., México, D.F.