El advenimiento de las computadoras digitales significó para la ingeniería estructural un gran paso de avance pues permitió la implementación de una podero,a herramienta de cálculo conocida como Análisis Matricial de Estructuras. A partir de esa realidad ha habido un gran desarrollo en el estudio de todo lo relativo con esa forma de cálculo, y nuestro objetivo en este trabajo. dearrollar la matriz de rigidez de un elemento en el cual uno de sub nodos renga la posibilidad de moverse en una dirección cualquiera a través de un apoyo de tipo deslizante.
Como es sabido, un punto ubicado en un plano tiene la posibilidad de moverse a lo sumo, según tres direcciones independientes, a saber, dos traslaciones y una rotación; En un elemento estructural que esta conectado a dos puntos extremos habrá entonces 6 patrones de movimiento diferentes: si este elemento se restringe contra toda posibihdad de movimiento. se tomará cinemáticamente determinado.El estudio de la rigidez del elemento. resultante de uno cualquíera de los movimientos que se han restringido. se hace liberando al elemento de la restricción y puesto en la dirección de ese movimiento y calculando las acciones estructurales que se derivan de esto.Cuando se ha hecho este cálculo para las 6 restricciones las acciones calculadas,escritas organizadamente, constituyen la matriz de rigidez del elemento.
En el caso que nos ocupa, las restricciones impuestas serán 5. en vista de que, como se ha placado, este elemento tendrá un apoyo de tipo deslizante y por lo tanto las acciones derivadas de ese movimiento son nulas, por tratarse de un movimiento de cuerpo rígido.
Existen varias técnicas para calcular las acciones producidas en una barra por un desplazamiento: entre las más usadas para estos fines el método de la liga conjugada, el uso de funciones de forma, métodos basados en el principio de conservación de la energía entre otras. Para el estudio que llevaremos a cabo utilizaremos el método de las fuerzas ó de compatibilidad de deformaciones, por considerarlo el más apropiado en este caso.
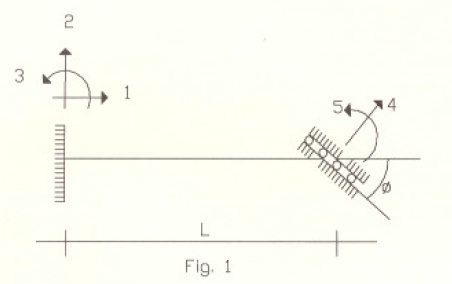
En la Fig 1 .muestra el modelo estructural del elemento y se identifican las direcciones de los posibles movimientos del mismo. Como se dijo anteriomente, el movimiento en la dirección de desliwmiento del apoyo no se puede incluir por Lmtarse en ese caso de un movimiento como cuerpo rígido que no produce acciones estructurales.
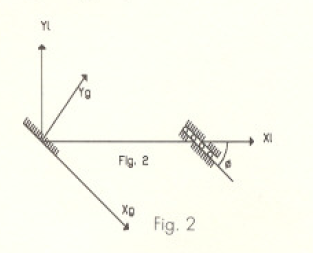
Puesto que un empotramiento puede transmitir 2 componentes independientes de fuerzas y un momento, es ventajoso analizar el elemento en unas direcciones tales que uno de los ejes coordenados ( El eje X-X en este caso) coincida con la dirección de deslizamiento del apoyo deslizante. Llamaremos a estos ejes: Xg, Yg. En la figura 2 se muestran los ejes Xg, Yg así como los ejes denominados X,, Yr Note que el ángulo entre estos ejes se mide del eje Xg, al eje Xj en dirección antihoraria.
Luego de realizar los cálculos descritos anteriormente se procederá a expresar la matriz de rigidez calculada en dirección de los ejes X,, Yr Esto se lleva a cabo mediante la transformación matricial [K,] = [T][Kg][TT] (Ec- 1). Aquí [T] es la matriz de transformación de coordenadas y [T7] es la transpuesta de dicha matriz.
En la figura 3 se han renumerado los posibles movimientos, o grados de libertad, según las direcciones Xg, Yg. Se hace evidente que los movimientos del elemento en las direcciones 1 y 4 son movimientos de cuerpo rígido y por lo tanto no producen acciones estructurales, quedando solamente por estudiar los movimientos en las direcciones 2, 3, 5 y 6.

Movimiento en la dirección 2
Para estudiar ese movimiento y las acciones producidas por el mismo. liberamos el elemento de la restricción en esa dirección resultando una estructura hipotética de primer grado, Fig.4, la cual calculará por el método de las fuerzas. Se elige como incógnita hipotetica el momento denominado M, en la Fig 5:y le aplicamos una fuerza unitaria en la dirección 2. Eso hace así pues para calcular el desplazamiento en la dirección 2 según el método del trabajo virtual, se aplicará nuevamente una fuerza unitaria en la dirección 2: La deformación así calculada se conoce como la flexibilidad del elemento en la dirección 2. la deformación así del clememo en la d irección considerada causada por una fuer7.a unitaria actuando en esa misma dirección. Se nota que esta fuerza introduce tanto flexión como fuerza axial en el elemento y por lo tan to ambos efectos deben ser considerados en el cálculo de las deformaciones.

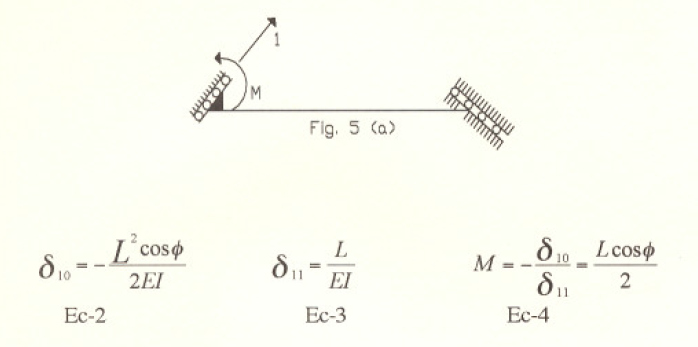
Análisis estructural del sistema base.
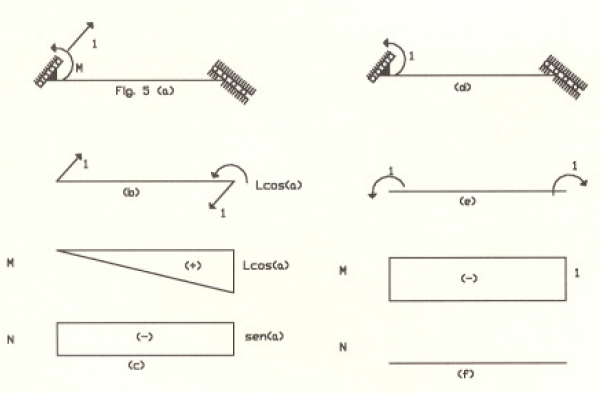
Con estos resultados, los diagramas definitivos de momento flexionante y fuerza axial serán los mostrados en la Fig 5g.
DIAGRAMAS DEFINITIVOS
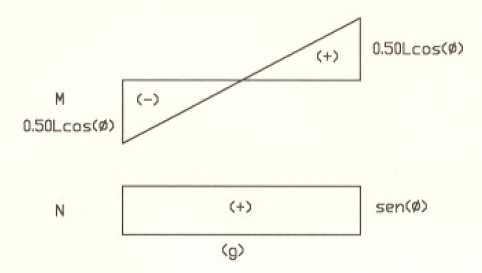
Y la deformación en la dirección 2 causada por una fuerza unitaria aplicada en la dirección 2. es decir, la flexibilidad en esa dirección se calcula según el método del trabajo vinual como:
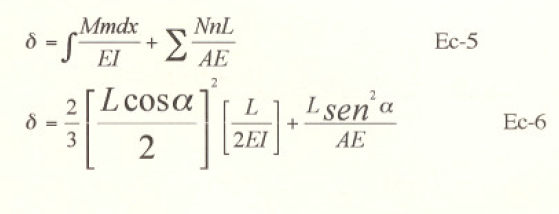
y puesto que la rigidez es el inverso de la flexibilidad:
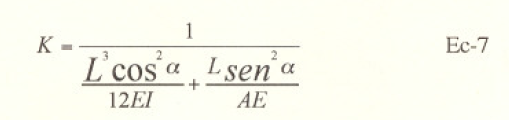
para fines de organización llamaremos a este termino k22 en la matriz de rigidez. y los otros términos correspondientes a este movimiento, se calculan por proporcionalidad de la ley elástica y resulmn ser:
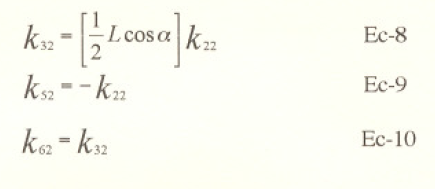
Movimiento en la dirección 3
Para medir el movimiento en la dirección 3 y las acciones resultantes liberamos la estructura de la restricción en la dirección 3, resultando una estructura hiperestática de primer grado, la cual se estudia con ayuda de los método antes expuestos y se obtienen los elementos de la columna 3 de la matriz de rigidez, que se resumen a continuación:
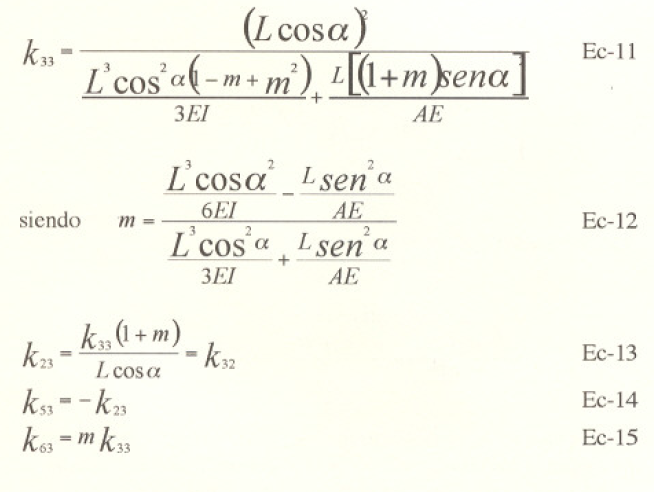
Finalmente, el estudio de los movimientos en las direcciones 5 y 6 dará los mismos resultados (con los adecuados) que los movimientos en las direcciones 2 y 3.resultando la matriz del elemento de la forma:
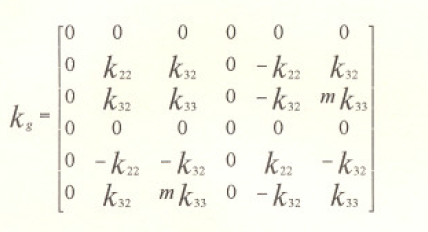
Como fue dicho anteriormente la matriz de rinde. expresada en coordenadas X,, Y,, se calcula por medio de la transfomación matricial:
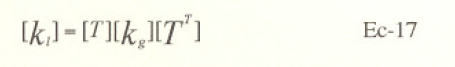
siendo [T] In matriz de transformación ele coordenadas dada por:

El resultado de esta transformación es la matriz de rigidez en coordenadas local del elemento con apoyo deslizante, la cual se muestra a continuación

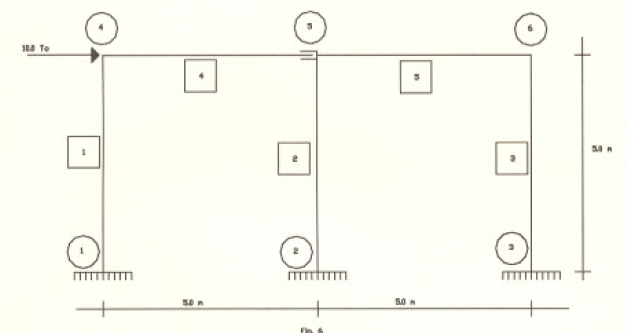
A continuación presentaremos un ejemplo teórico del concepto que hemos desarrollado. El ejemplo consiste en el análisis estructural del pórtico mostrado en la fig 6.
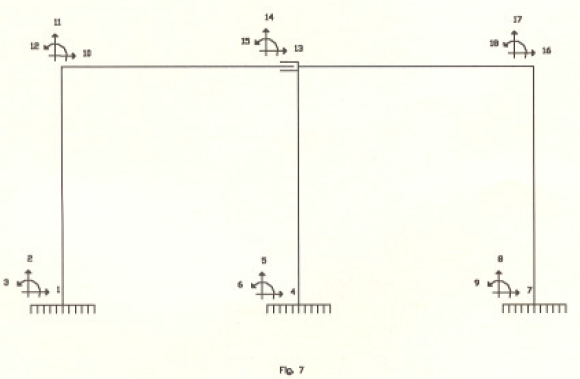
Supongamos que la barra 4 este unida en el nudo 5 mediante un apoyo del tipo deslizante que hemos estudiado con un ángulo de deslizamiento de 0 grados, es decir, que puede deslizarse horizontalmente dentro del nudo 5. El sentido común nos indica que para la solicitación mostrada, la columna 1 debe absorber toda la carga de 10 toneladas aplicada al nudo 4 y que la viga 1, al poder deslizarse libremente en dirección horizontal, no tomara carga axial alguna. Los cálculos se presentan a continuación en formato matricial y fueron elaborados en una pagina Excel. En la Fig 7 se describen los grados de libertad considerados. La estructura fue resuelta también por el método de las fuerzas, [ver anexo 1] dando resultados coincidentes.
ANEXO 1
Solucion por el método de las fuerzas
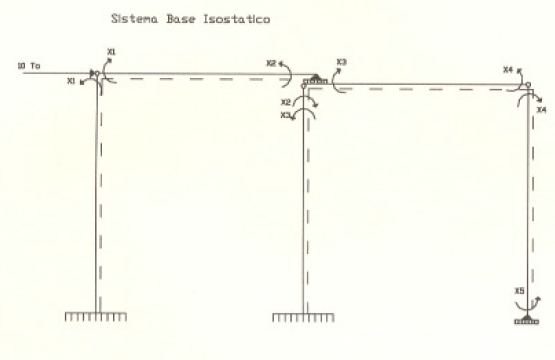
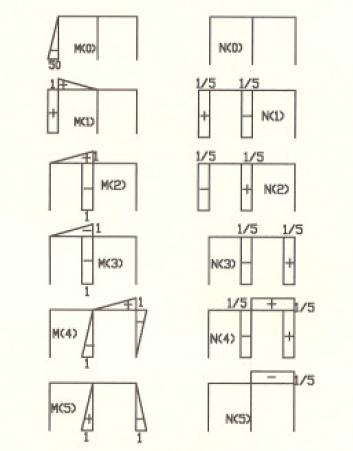
Diagrama de Momentos y Axiales en el Sistema Bao;c hostático.
Conclusiones
AI finalizar este estudio debemos reconocer que su valores mayormente teórico hasta ahora; y quizá el mayor aporte que puede obtenerse del mismo es la conclusión de que la rigidez debe definirse como el valor de la acción que debe ser aplicada en un punto, en una dirección específica para producir un desplazamiento unitario relativo de dicho punto CON RELACIONA SU POSICIÓN NO DEFORMADA en la dirección de la acción aplicada, en vez de la definición tradicional, que considera el desplazamiento relativo del punto con relación al nodo opuesto de la barra. Nuestra definición se ajusta perfectamente a la condición de que los demás desplazamientos en el elemento considerado deben ser nulos cuando se provoque el desplazamiento unitario en la dirección específica para la cual se calcula la rigidez. Nótese por ejemplo que de acuerdo a una definición que implique un desplazamiento relativo entre los extremos del elemento, si el ángulo de deslizamiento del apoyo es cero la barra debería tener una rigidez infinita para producir ese desplazamiento relativo, en virtud de que en ese caso se movería como cuerpo rígido, y como se ha hecho notar, un movimiento de ese tipo no produce acciones estructurales en el elemento; en cambio, si el desplazamiento se considera como relativo del punto en cuestión con relación a su posición no deformada, la rigidez en este caso es cero como debe ser.
Otro resultado digno de notar es que en un elemento de este tipo el coeficiente de transmisión de momento cuando se estudia la rigidez en la dirección 3 ó 6 no es el familiar +(1/i), sino que es un valor que varia en función del ángulo de deslizamiento y va desde +(Vi) para un ángulo de 0 grados hasta -(1.00) para un ángulo de 90 grados
Aunque este estudio está en el campo de lo puramente teórico. esperamos que sea una contribución que enriquezca el conocuniemo ayude en la precisión de los conceptos envueltos y sirva en el futuro cuando pueda encontrarse una aplicación práctica del mismo.
Bibliografía
Davies, G. Virtual Work in Structural Analysis.: John Wiley. Chichester
Hirschfeld, K. 1975. Estática en la Construcción. Editorial Reverte.
Hibbeller, R. 1979. Análisis Estructural. Prentice-Hall Hispanoamericana.
Kanchi, M. B. 1981. Matrix Methods of Structural Analysis.: John Wiley, New York.
Kardestuncer, H. 1975. Introducción al Análisis Estructural con Matrices. McGraw-Hill.
Laursen, H. 1978. Structural Analysis. McGraw-Hill, New York
Livesley, R. K. 1975. MATRIX METHODS OF STRUCTURAL ANALYSIS. Pergamon Press, Oxford.
McGuire, W. 1979. Matrix Structural Analysis. John Wiley, New York
McMinn, S. J 1964. Matrices for Structural Analysis. E. & F. N Spon Limited, London
Przmieniecki, J. S. 1968. Theory of Matrix Structural Analysis. McGraw Hill.
Wang, C. 1979. Introducción al Análisis Estructural con Métodos Matriciales. Compañía Editorial Continental.
