EXPANDRD: MODELO DE PLANIFICACIÓN DE EXPANSIÓN DE LARGO PLAZO GENERACIÓN/RED PARA REPÚBLICA DOMINICANA

 

i. Introducción

Al igual que casi todos los sectores económicos de la sociedad. el com­portamiento de los sistemas eléctricos está sujeto a una serie de incerti­dumbres que dificultan la tarea de planificación y finalmente. la toma de decisiones de inversión. Particularmente en el sector eléctrico. el tamaño de los sistemas interconectados, la incertidumbre de la demanda y precios futuros, la hidraulicidad y la disponibilidad de los equipo. convienen el problema de planificación de expansión en un problema de gran escala, estocástico y combinatorio.

Dada la complejidad del problema por su naturaleza no lineal con varia­bles discretas y las elevadas cantidades económicas envueltas, se requiere disponer de modelos matemáticos que representen correctamente el funcionamiento los medios de producción. al tiempo que crean capaces de encontrar soluciones robustas y flexibles que permitan optimizar las decisiones.

El objetivo de este trabajo consiste en el desarrollo de un modelo que sirva de apoyo en la loma de decisiones frente a problemas de selección de inversiones y planificación de la operación del Sistema Eléctrico Do­minicano. debiéndose determinar un plan de obras indicativo óptimo. Asi­ mismo el modelo deberá proporcionar información de: la tecnología del equipo generador. su localización, tamaño y fecha de puesta en servicio; los tramos de red que deben ser ampliados y la fecha de puesta en servi­cio; y los costos los marginales de operación y su evolución futura que surgen como su producto de la solución del problema de optimización.

ii. Estado del arte

A. Modelado del Sector Eléctrico

Hoy en día. las metodologías y técnicas de cálculo empicadas para el diseño de modelos de planificación del sector eléctrico son muy diversas. En general requieren un signficativo esfuerzo de modelado y consumen importantes  recurso computacionales, por lo que se han desarrollado técnicas específicas dependiendo del uso concreto que se quiera dar al mode­lo, es decir, atendiendo a su ámbito preferente de utilización.

El ámbito de utilización de los modelos suele definir un problema conceptual distinto que normalmente requiere una metodología de diseño del modelo también distinta. En el sentido más amplio de los modelos atendiendo a las caractcrísticas del modelado del Sector Eléctrico, pueden agruparse según el marco regulatorio en que se desenvuelve el negocio de generación, en: modelos de entorno tradicional y desregulado

La teoría marginalista demuestra que en competencia perfecta el comportamiento del mercado se puede representar teóricamente a través de un único problema de optimización basado en la minimización de los costos de todo el sistema necesarios para el suministro de la electricidad demandada Las condiciones necesarias para la existencia de competencia perfec­ta se dan cuando hay un gran número de pequeñas empresas produciendo un bien homogéneo y una cantidad demasiado pequeña como para influir en el precio del mercado.

En los mercados eléctricos reales de reciente liberalización no se sue­len dar las condicione que garantizan la competencia perfecta debido a que estás están formado, normalmente por un número reducido de gran­des empresa, productoras. En el caso dominicano, por están organizado el mercado de generación como un mercado donde los, costos de producción y las indisponibilidades de los equipos son declaradas. justificadas y auditadas, modelar el mercado como único problema de optimización basado en la minimización de los costos de todo el sistema, cobra sentido

B. Modelos de Entorno Tradicional

De la revisión bibliográfica realizada a los modelos de entorno tradicional estudiados, se pudo detectar la existencia del modelo SAPP LT desarrollado en el 2001 por investigadores de SAPP y de la Universidad de Purdue de los Estados Unidos. Este modelo en principio tendría una formulación similar a la del modelo ExpandRD que se desarrolla en el presente trabajo, con diferencias en el uso de variables binarias en la operación del equipo generador y de la red, lo que eventualmente lo convierte en un problema más difícil de solucionar.

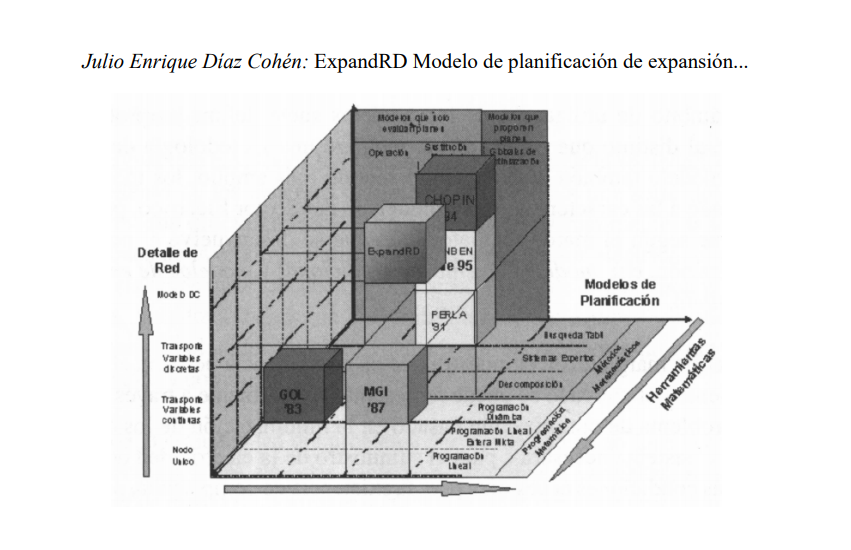
En dirección de la flecha la modelación implica mayor detalle y mayor requerimiento computacional.

iii. Modelo de planificación

A. Caracterización del Sistema

Dado que en los modelos de largo plazo la incertidumbre debida a la evolución de algunos parámetros cobra gran importancia, resulta imprescindible formular el problema como un problema estocástico. Por lo general los modelos más realistas son los modelos estocásticos, pero prosentan dificultad para poderlos resolver adecuadamente, por lo que muchas de las técnicas, aplicables a los modelos estocásticos tratan de reducir el problema a su versión determinista para poderlo resolver. En fin. para el tratamiento de este tipo de problemas suelen emplear,e dos técnicas bási­cas. las conocidos como restricciones aleatorias (chance constrained) y la obtención de los equivalentes deterministas.esta última sobre la cual se basa la formulación del modelo que se desarrolla en el presente trabajo.

Otro apecto que debe ser considerado. es la caracterización del siste­ma eléctrico representado en el modelo de planificación a desarrollar, que depende del objetivo y futuro uso del mismo. Es decir, se puede representar sistema de una forma simple con demanda conocido y agregadas en un único nodo hasta modelar de forma elemental la interconexión entre área considerando explícitamente las restricciones de la red así como las incertidumbres en la predicción de la demanda. Como es lógico a mayor precisión del modelado supone un aumento consiiderable en la carga computacional requerida. debiéndose establecer un compromiso entre un modelado de Ja realidad exhaustivo y un modelado simplista que podría proporcionar resultados no creíbles.

En el mismo sentido. otro aspecto relevante en los modelos de planificación es el alcance. Cuanto más corto es el alcance mayor debe ser el nivel de detalle, y cuánto más largo es, más importancia cobra la consideración de la incertidumbre. Un modelo de planificación a largo plazo requiere un detalle menor al modelar la operación dado que esta se extiende durante mucho tiempo y sería, por consiguiente inviable un modelo muy detallado.

B. Formulación Matemática

Así, tomando en cuenta, entre Otras, las consideraciones anteriores, el modelo que se desarrolla en el trabajo caracteriza el sistema eléctrico de la siguiente manera: alcance temporal de 15 años (la larga vida útil de los equipos que componen un sistema eléctrico exige que su construcción se justifique durante períodos de tiempos amplios); representación de la demanda mediante una curva monótona por bloques, y la incertidumbre en las previsiones de crecimiento de la demanda (debido a factores clima­tológicos y económicos) mediante escenarios asociados a su árbol de probabilidad: representación de las centrales térmicas mediante atributos de máximo y mínimo técnico. costos de inversión, consumo específico, tasa de indisponibilidad (fortuita y programada). localización de las centrales y el precio de combustible: y representación de las centrales hidroeléctricas de forma deterministica (se consideran las aportaciones como un valor medio histórico de la producción de los últimos 20 años).

El modelo de planificación planteado es de tipo lineal entero mixto, donde la función objetivo representa el valor presente de los costos de inversión y operación del sistema. Se trata de minimizar la función objetivo sujeta restricciones de abastecimiento. capacidad, etc..y dado un árbol de probabilidad de ocurrencia de la demanda, lo que hace al modelo ser un modelo planificación estocástica.

La formulación básica del modelo desarrollado es la siguiente:

Equivalente Determinista

Función Objetivo

Sujeto a

En donde n es el número de escenarios posibles y pi es la probabilidad asociada a cada uno de los escenarios.

Puesto que en la forma real de planificación los costos de operación e inversión luchan contra el costo de la energía uno suministrada, que cuantifica económicamente el perjuicio que la demanda experimenta por no ser suministrada. en  función objetivo se incluye explícitamente como una variable de decisión En este sentido. puede considerarse que la energía no suministrada cumple la función de lo que en un problema de optimización se conoce como una variable de holgura. Si el costo de la energía sumi­nistrada es mu) bajo. la inversión será muy pequeña e incluso nula. dado que resulta más barato no suministrar que invertir.

C. Implantación informática

El modelo que 'e ha desarrollado ha sido escrito en el lenguaje al­gebraico de programación matemática GAMS versión 20.5 desarrollado por GAMS Dcvelopment Corporation. y emplea como optimizador para el problema entero mixto el CPLEX. De hecho. la utilización de GAMS como lenguaje. garantía la adaptación del dimensinamiento del progra­ma al caso de estudio. De esta manera consigue una flexibilldad total en su uso. no asociada al problema a resolver en lo que respecta a la entrada de datos

Se ha desarrollado un módulo escrito en lenguaje GAMS (ExpandRD. gms) que contiene el código matemático del problema de optimizacicón. y una  interfaz en Excel que permite la entrada y salida de datos a los fiche­ros en forma Lo de texto mediante una hoja de cálculo. Se hace importante destacar que la estructura ele estos ficheros permite la lectura de todos los dato con independencia del tamaño del sistema a analizar.

iv. Caso de estudio

Para el caso concreto del Sistema Eléctrico Dominicano. se elaboró un estudio de aplicación que permitiera realizar una planificación óptima de la expansión de generación-red de largo plazo.dando indignación del crecimiento requerido de generación y transmisión en las distintas zonas para atender adecuadamente la demanda prevista en el horizonte del estudio. Esta planificación de largo plazo tiene como objetivo servir de marco de referencia hacia el cual deben tender todos los resultados de corto y mediano plazo, proporcionando un norte.una meta clara hacia la cual deben tender toda estrategia de expansión propuesta para el sistema.

Una vez comprobada de forma práctica el adecuado funcionamiento del modelo de los resultados e pudieron extraer las siguientes conclusiones:

Para suplirlo, incrementos de demanda anuales de manera óptima deben hacerse un significativo esfuerzo para incentivar la instalación de aproximadamente 2.250 MW en los próximos 10 años Con este estudio se observa también el hecho eminente de un cambio tecnológico en generación hacia unidades térmicas de carbón, lo que modifica el despacho desplazando las cent reales menos eficientes. Los motores diesel con F0#6 definen el costo marginal de largo plazo cumpliendo con la transmisión eléctrica y desplazando inversiones.

Como producto de la entrada de nueva; unidades se observa una reducción de los marginales esperados del orden del 31% (32.4 milis/kWh) en promedio en el año 2010.respecto al año 2004 (46.6 milis/ kWh).

Se deben emprender proyectos que sean capaces de evacuar la generación adicional hacia los principales centros de consumos. La zona critica a ser estudiada es la zona norte y sus enlaces con la zona centro del sistema. En el mediano y corto plazo aparece bastante clara la necesidad de reforzar los enlaces 2610QUIN - 2400CA38, 2370PPL1 - 2220LVEG y 1260HA69 - 1170LMIN.

v. Conclusiones

En cuando a la caracterización del sistema representado en el modelo se deduce que: la elección del alcance temporal de 15 años con periodos anuales fue adecuada; asi mismo la modelación de las centrales hidroeléctricas de manera determinista permitió que para la revolución del problema se consumieran menos recursos computacionales, permitiendo considerar el modelado de los mínimos técnicos de las unidades térmicas y el acopla­miemo de operación de los distintos corredores de la red.

A pesar de ser una alternativa de desarrollo “impuesta”, dada por dispnibilidad del lenguaje de modelado GAMS dentro de la empresa y la ausencia de otros, GAMS resulta adecuado para posteriores refinaciones y avances sobre el código, dimensionamiento del sistema y utilización de otros algoritmos de optimización. El desarrollo de la interfaz en Excel permite que la ejecución del modelo sea independiente de la plataforma de desarrollo GAMS para el usuario final.

vii. Biobliografía

Alonso, J.F.; Sáiz, A.; Martín, L. PERLA: An Optimization Model for Long Term Expansión Planning of Electric Power Transmission Networks. Red Eléctrica de España S.A., 1991.

Binato, Silvio; Couto, Gerson; Lizardo, Joao. A Greedy Randomized Adaptive Search Procedure for Transmission Expansión Planning. IEEE Trans. on PAS. Vol. PAS-16, N. 2. 2001.

Bloom, J.A. Long Range Generation Planning Using Descomposition and Probabilistic Simulation. IEEE Trans. on PAS. Vol. PAS-101, N. 4. pp. 797-802. 1982.

Bowen, Brian H.; Sparrow, F.T. SAPP, User Manual for the Long Term Model. Purdue University-USA, 2001.

Brooke, A.; Kendrick, D.; Meeraus, A. GAMS. A User’s Guide. GAMS Development Corporation. Washington, DC. 1998.

Chiang, Angela S.; Wu, Félix; Baraya, Pravin. A Game-Theoretic Model for Generation Expansión Planning: Problem Formulation and Numerical Comparisons. IEEE Trans. on PAS. Vol. PAS-16, N. 4. 2001.

Garver, L.L. Transmission NetWork Estimation Using Linear Programming. IEEE Trans. on PAS. Vol. PAS-89, N. 7. pp. 1688-1687. 1970.

Kaltenbatch, J.C.; Peshon, J.; Gehrig, E.H. A Mathematical Optimization Technique for the Expansión of Electrical Power Transmission Systems. IEEETrans. onPAS. Vol. PAS-89,N. 1. pp. 113-119. 1970.

Lapiedra, Luis; Ventosa, Mariano; Linares, Pedro. Expansión Planning Model Considering an Emission-Based Permits Market. Instituto de Investigación Tecnológica. Universidad Pontificia Comillas Madrid, 2002.

Latorre-Bayona, Gerardo; Pérez-Arriaga, Ignacio J. CHOPIN, A Heuristic Model for Long Term Transmisión Expansión Planning. Universidad Industrial de Santander-Colombia, 1994.

Latorre-Bayona, Gerardo; Cruz, Rubén; Areiza, Jorge; Villegas, Andrés. Classification of Publications and Models on Transmission Expansión Planning. IEEE Trans. on PAS. Vol. PAS-18, N. 2. 2003.

Levi, V. New Mixed-integer Methodology for Optimal Transmission Expansión Planning. Electric Power Systems Research, Vol. 32, N. 3. pp. 227-238. 1995.

Masse, P; Gilbrat, R. Application of Linear Programming to Investments in the Electric Power Industry. Management Science, Vol. 3. N. 2, pp. 149-166. 1957.

Mejía Villegas S.A. Estudio Eléctrico de Planeación. Organismo Coordinador del Sistema Eléctrico Dominicano. Santo Domingo, 2002.

Monticelli, A. Interactive Transmission NetWork Planning Using a least Effort Criterion. IEEE Trans. on PAS. Vol. PAS-101, 1979.

Olmedo, Juan Carlos. Modelo GOL. Santiago de Chile, 2001.

Park, Y.M.; Park, J.B.; Won, J.R. A Genetic Algorithms Approach for Generation Expansión Planning Optimization. Symposium on Power Systems on Power Plant Control, Pergamon, UK. Pp. 257-262. 1996.

Pereira, M. V.F. A Descomposition Approach to Automated Generation/Transmisión Expansión Planning. IEEE Trans. on PAS. Vol. PAS-104, N. 11. Nov. 1985.

Ramos, Andrés; Sánchez, Pedro. Modeling Transmission Ohmic Losses in a Stochastic Bulk Production Cost Model. Instituto de Investigación Tecnológica, Madrid 1997.

Ramos, Andrés. Modelos de Explotación a Medio Plazo de la Generación Eléctrica. Aplicaciones para el Sistema Español. Tesis para obtención del grado de Doctor Ingeniero Industrial. Universidad Politécnica de Madrid, 1990.

Teire, R.C.G.; Silva, E.L.; Fonseca, L.G.S. A Cooperative Expert System for Transmission Expansión Planning of Electrical Powers Systems. IEEE Trans. on PAS. Vol. PAS-13, N. 2. 1998.

Urrutia-West, Juan Pablo. Planificación de la Expansión de Sistemas Eléctricos Vía Descomposición de Benders. Tesis de Grado, Pontificia Universidad Católica de Chile, 1995.

Ventosa, Mariano; Rivier, Michel; Ramos, Andrés. Electricity Market Modeling Trens. Instituto de Investigación Tecnológica. Universidad Pontificia Comillas Madrid, 2002.

Wen, F; Chang, C. S. Transmission NetWork Optimal Planning Using The Tabú Search. Electric Power Systems Research, N. 42. pp. 153-163. 1997.