MATERIALES COMPUESTOS REFORZADOS CON FIBRA

Conocimientos previos

Fibras ‐ elementos de forma larga y cilindrica de gran resistencia y/o boro, tungsteno, óxido de aluminio, etc...., con un diámetro entre 6 y 100 micrones (1 micrón = 10'⁶m).

Matriz ‐ material que ata las fibras y transmite cargas u las mismas atravé de uniones químicas o mecánicas. Los materiales de matrit de uso más común son los polímeros. tales como las resinas de epoxia endurecidas por calor y metales de bajo punto de fundición como el aluminio.

Este laboratorio requiere un conocimiento general de los conceptos y parámetros que conllevan el comportamieto elástico de materiales. a saber tensión. módulo clásico y coeficiente de Poisson.

Objetivos

En este laboratorio, la dala será recolectada para cumplir con los siguientes análisis concernientes a la caracterización y al comportamiento elástico de materiales compuestos reforzados con fibra.

1. Calcular la fracción en volumen de fibras, f_f para una secciones orientadas 

a) Perpendicular a las fibras y

b) 45° a las fibras. Comparar estos dos valores y tomar en cuenta si hay algunas diferencias

2. Calcular los módulos longitodinal y transversal, E₁ Y E₂, a partir de data provista para un compuesto de goma reforzado en nylon y comparar estos valore' con aquellos observados en el laboratorio.

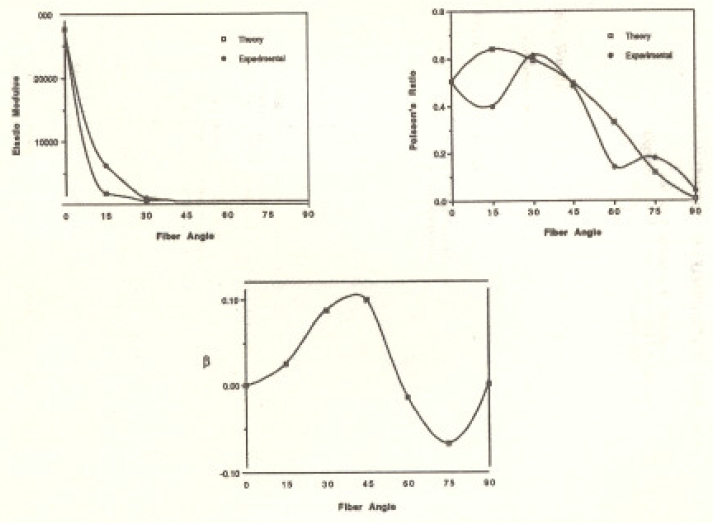
3. Calcular el módulo elástico. E, en diferentes ángulo' (i.e. =15°.30°, 45°,60°. y 75°} y graficar los valores como una función de. En la misma gráfica. trazar 1:1 curva teórica de la ecuación dada y comparar las dos.

4. Obtener el mayor coeficiente de Poisson V₁₂ medido en los distintos ángulo;. y graficar los valores junto con la curva teórica para hacer una comparación.

5. Graficar los valores observados del módulo de acoplamiento de acoplamiento como una función de 0.

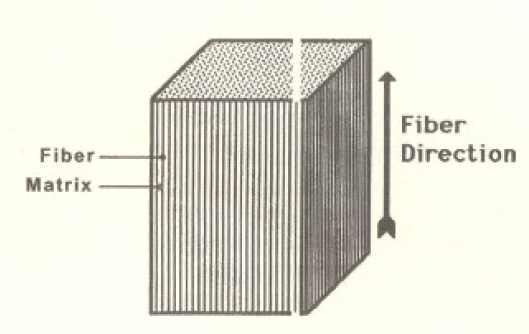
Fig.1 Sección típica de un material compacto reforzado con fibra, las fibras son continuas orientadas a una misma dirección.

Determinación del contenido de fibra

El contenido de fibra de un determinado compuesto es generalmente expresado como la fracción en volumen de fibra y se denota f_f. La mayoría de los compacto estructurales contienen entre 50 y 60 por cierno de fibra (0.5 < f <0.6) mientras que compuestos en otras aplicaciones pueden contener menos.

Un método utilizado para determinar el contenido de fibra es llamado método de conteo de puntos. Este consiste en colocar una parrilla o un grupo de puntos sobre un foto micrográfico de una sección transversal pulida del material compuesto. Favor notar que para poder obtener una medición precisa, los puntos deben ser pequeños en comparación con el diámetro de la fibra. Al contar el número de puntos o intersecciones que caen sobre la fibra y luego dividiendo por el número total de puntos, la fracción del área es calculada.

Refiriéndonos a la Fig.2, el número de puntos que caen dentro del área de fibra es alrededor de 155 (no todo el mundo contará la misma cantidad, aún se le dé la misma figura). El número total de puntos en el grupo es (exactamente) 630 así que el área de fracción de fibra en este ejemplo es 155/630 ss 0.25.

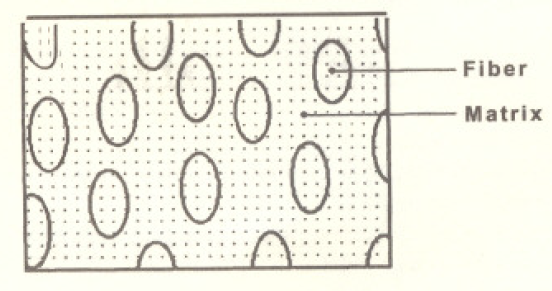
Fig. 2  ejemplo del método de conteo de puntos para un compuesto reforzado con fibra.

Notar que las áreas de fibras son elípticas; ¿significa esto que estas fibras no son circulares en la sección transversal?, ¿Pudieran ellas ser circulares pero cortadas en un ángulo?, ¿Pudiera el ángulo al cual las fibras están cortadas cambiar el área de fracción de fibra obtenida por el método de conteo de puntos?

Considere el caso donde las fibras están cortadas en el ángulo correcto según su longitud. Las áreas serían circulares y el área de fracción podría ser obtenida como dijimos anteriormente. Claramente, esta área de fracción A_f, es la misma que la fracción de volumen f_f. Es más, no importa a que ángulo las fibras sean cortadas; aún las fibras estén orientadas al azar, tal como un compuesto que contiene fibra troceada, el método de conteo de puntos da, directamente, la fracción de volumen de los componentes.

En este laboratorio. sin embargo.el área total de fibra será determinado al contar el número de fibras que intersecan la superficie de la muestra y multiplicado por el área de la fibra. Esto es posible debido al recativamente gran tamaño del reforzamiento de nylon y el bajo contenido de fibra. Este método será utilizado en una superficie orientada perpendicularmente a las fibra y otra orientada a 45º de las fibras.

Comportamiento elástico

Como mencionamos anteriormente, el comportamiento mecánico de materiales compuestos reforzados con fibra es altamente dependiente de la dirección en que una propiedad panicular es medida. Por ejemplo, el modulo elástico a lo largo de las fibras. E, es dependiendo diferente al módulo elástico transverso a las fibras. E, Las primeras aproximaciones de esto módulos pueden ser calculadas a partir de las constantes elásticas de los materiales componentes. considerando los modelos de iostrain e isostress mostrados en la Fíg.3

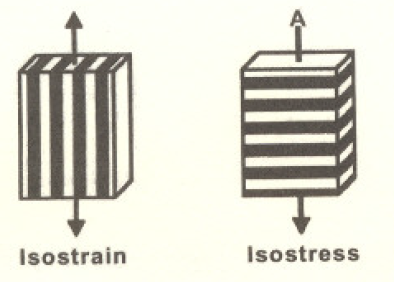
Fig. 3 Geometría de materiales compuestos unidireccionales idealizados

La ecuación para el módulo longitudinal (a lo largo de las fibras) puede ser derivada del modelo iostrain como:

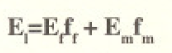
Donde:

E_f= Modulo elástico de las fibras
f_f = Fracción volumétrica de la fibra en el compuesto
E_m = Modulo elástico de la matriz
f_m= Fracción volumétrica de matriz = (1-f_f )

Esta ecuación se le conoce como la regla de mezclas e implica que la contribución de un componente es directamente proporciona la su fracción de volumen. Claramente, la ecuación para la densidad del compuesto sería de la misma forma.

La ecuación para el modulo transverso (perpendicular a la dirección de la fibra) puede ser derivada del modelo isostress como:

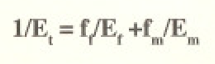
Esta ecuación es conocida como la regla de mezclas inversa. Ambas ecuaciones son mostrada. o, en la Fig.4 para ilustrar el efecto del contenido de fibra en el módulo elástico. Notar que el modulo transverso no se incrementa apreciablemente más allí del modulo del componentes menos rígido.la matriz contenido de fibra usualmente encontrando en compues­tos dirigidos.

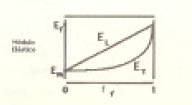
Fig. 4 Módulo elástico versus volumen de fracción de fibras para los modelos isostress e isostrain.

Nos podemos referir a las direcciones 1 y t como los ejes de material y, si el compuesto es tensado en cualquiera de estas direcciones, las tensiones correspondientes pueden ser calculadas (a la izquierda en la Fig.5) Sin embargo, si la tensión es aplicada en un ángulo agudo, 0, a las fibras (a la derecha en la Fig.5), la respuesta elástica a lo largo de los ejes de distribución de carga (1,2) puede ser calculada a partir de las propiedades medidas a lo largo de los ejes de material (1 y t).

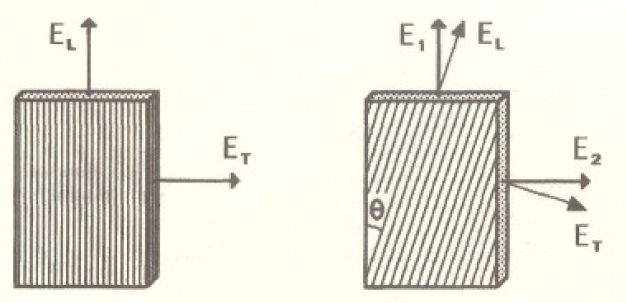
Fig.5 ilustración de geometrías de material (1 y t ) y carga/ distribución de carga ( 1.2).

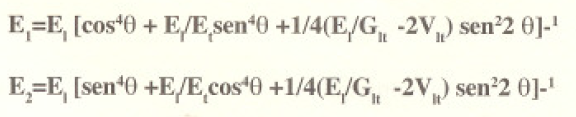
Notar que en las ecuaciones anteriores los parámetros de materiales necesitados incluyen 0, G_lt y V_jt, Ej y E. El valor de E, puede ser calculado a partir de la ecuación de la regla de mezclas dada anteriormente y el valor obtenido será satisfactoriamente cerca de la realidad (aunque el compuesto esté hecho de fibras en una matriz en vez de planchas alternas como se utiliza en el modelo isostrain).

Sin embargo, el valor de E_t calculado a partir de la ecuación de la regla de mezclas inversa no estará cerca de la realidad porque el modelo isostress (planchas amontonadas) es una simplificación excesiva de un compuesto de fibra. Similarmente, ecuaciones para G_lt (el modulo de corte obtenido cuando una torsión es aplicada en el plano perpendicular a la dirección de la fibra) no siempre dan valores precisos; por lo tanto, E y G_lt deben ser medidos en el laboratorio. El mayor coeficiente de Poisson, V_lt (un esfuerzo longitudinal causa una tensión en la dirección transversa), puede ser calculado confiablemente a partir de una ecuación tipo la regla de mezclas tal como el El.

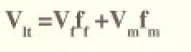
¿Y qué del V^t1 (un esfuerzo transverso causando una tensión en dirección longitudinal?

¿Esperarías que fuera igual al V^lt? Es verdadera mente diferente pero 11 fácilmente calculable como sigue:

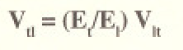
La transformación del V Ca lo largo de los ejes de material) al V., (a lo largo de lo; eje de constribución de carga) es dada en la ecuación siguiente:

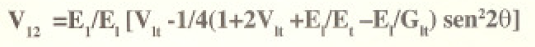
Uno de los fenómenos más importantes que ocurren Obre la distribu­ción de carga fuera de eje de compuestos unidireccional reforzados con fibra es la producción de una deformación de corte a partir de un estado de pura tensión. Como'e ilustra en la Fig.6. si un ángulo de referencia de 90º es inscrito en la muestra (antes de cargar). este ángulo cambiará a medida que la muestra sea cargada uniaxialmente. indicando la exitencia de una deformación de corte. Claramente, esto no ocurriría con un material isotrópico cuadrado se conocería en un ángulo pero los ángulos no cambiarían) o con una muestra de un compuesto cargado a lo largo de los ejes del material (0= 0° 6 9= 90°).pero cuando O está entre 0° y 90°. una deformación de corte usualmente ocurre.Puede que sea positiva, o negativa, o cero, dependien­do del valor de O. las propiedades elásticas de los componentes y el corte­ nido de fibra del compuesto.

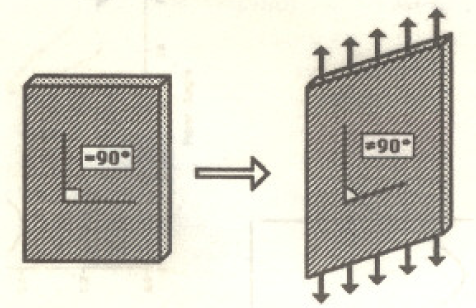
Fig.6 ilustración de una deformación de corte producida por una distri­bución de carga de tensión de un compuesto de fibra.

La cantidad de cambio en el ángulo de 90º (medido en grados) que ocu­rre sobre la tensión del compuesto es la deformación de corte Y12 Para el propósito de nuestro simplificado experimento, definiremos un coeficiente de acoplamiento de deformación. para relacionar In tensión normalmen­te aplicada G,.con la deformación de corte resultante. tal como sigue:

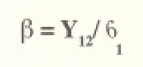
Notas del instructor

Las muestras de compuesto utilizado para este experimento consisten de 7% de volumen de cuerda de nylon en una matriz de goma curada. Se puede sugerir contactar a un fabricante de llantas para este supo de material no curodo. refonado unidireccionalmente. Un experimento similar puede ser llevado a cabo con fibra de vidrio/epoxia o grafito/cpoxia, pero las desviaciones podrían ser solamente medibles con un medidor de deformación. Otros materiales de planchas reforzadas comercial mente disponibles pueden basiar, siempre y cuando la exteosibilidad sea suficientemente alta para permitir la medición manual de la distorsión de corte y deformación.

Para este ejercicio. los estudiantes deben medir las elongaciones (y contracciones transversas) con un Calibrador Dial y la deformaciones de corte con un transportador. Muestras de posibles resultado;son presenta· das en lo siguiente

Breve mirada a los materiales compuestos

Un material compuesto es un sistema de materiales construidos por la mezcla o combinación de dos o más micro o macro-constituyentes que defieren en forma y composición química y que son esencial mente asociables entre sí.

La importancia de un material compuesto radica en que dos o más ma­teriales distintos se combinan para formar un material compuesto cuyas propiedades sean superiores que las de sus componentes.

Los compuestos se clasifican en tres categorías:

1) Con partículas, el concreto; (mezcla de cemento y grava).
2) Con fibras, la fibra de vidrio, (la fibra ele vidrio incrustado en un polímero).
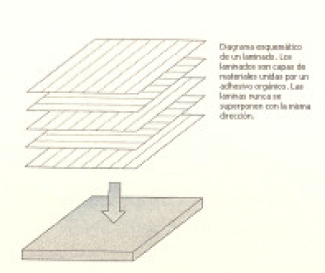
3) Laminares (la madera contrachapada o triplay)

Compuestos reforzados por dispersión

Los materiales endurecidos por dispersión contienen dispersoides(partículas de oxido metálicos muy pequeña• 10 a 250 nm de diámetro) en u na matriz de metal. Los mismos interfieren con el deslizamiento. dan­do buenas propiedades mecánicas a temperaturas elevadas. (Bloquean el movimiento de las dislocaciones y producen un pronunciado efecto de endurecimiento, su resistencia a la termofluencia es superior a la de los metales y aleaciones).

Materiales compuestos paniculados que contienen grandes cantidades de panículas grouesas que no bloquean con eficacia el deslizamiento se diseñan para producir combinaciones poco usuales de propiedades (no se puede mejorar la resistencia); algunas de estas propiedades dependen solo de las cantidades y propiedades relativa de los constiruyentes individuales.

La regla de la mezcla ayuda a determinar estas propiedades con exactitud.

Regla de la mezcla

Determinación de la densidad

P_C = ∑(f_i p_i) f₁ p₁ +f₂ P₂ +......+ f_n p_n
p_c = densidad del compuesto
P₁ p₂ = densidad de cada constituyente
f₁ f₂ = fracción volumétrica de cada constituyente

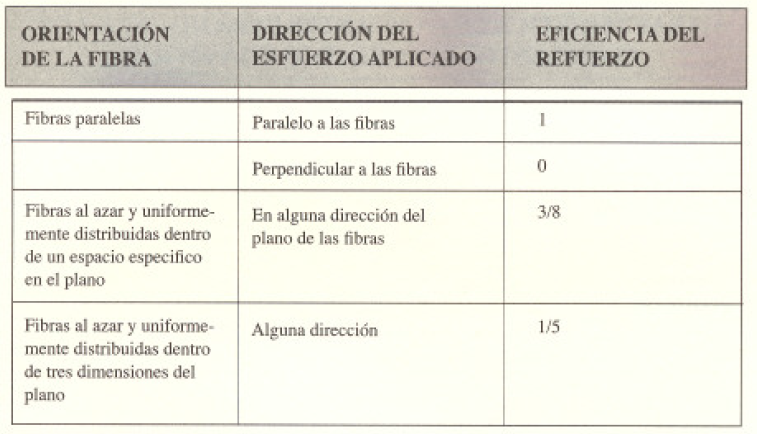
COMPUESTOS PARTICULADOS VERDADEROS

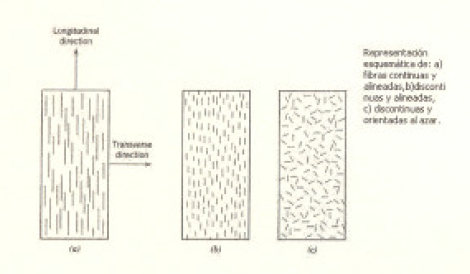
En general. cuando no se especifica. se entiende por compuesto a aquel material formado por fibras rectas y largas, sitúa en el interior de una matriz que mantienen a las fibras unidas y distribuye los esfuerzos. Las fibras soponen la mayor pone de las cargas. mientras que la matriz se responzable de la tolerancia al daño (golpes) y del componamiento a fatiga. Una fibra es una multuud de fibras. Por lo tanto. lo que es ve a "imple vista se llama bundle o yarn. Un bundle puede tener 3 310 a 12 103 fibras. Las fibras ofrecen sus mejores propiedades cuando trabajan en la dirección de la fibra. es decir, que en un caso ideal deberían alineas las direcciones de las fibras con la dirección de la fuerza exterior.

Las fibras se sitúan en capas o laminas supercompuestas en la dirección de espesor obteniendo estructuras que se llaman laminados. Las láminas nunca se superponen con la misma orientación. Se deberá estudiar a fondo la secuencia de aplicación y orientación adecuada para cada ca.o. La se­cuencia de aplicación y orientación tiene mas importancia incluso que las caracteristicas físicas de las fibras y matriz y variando secuencia de aplicado y orientación se pueden conseguir infinitos comportamientos. Jugando con estos parámetros se pueden conseguir comportamientos radicalmente diferentes en resistencias, rigidez, tolerancia al daño. estabilidad dimensional o de laminación.

En el cálculo  correcto de piezas de materiales compuestos. la geometría y el material (fibras.matriz, secuencia de apilado y angulación) deben dise­ñarse a la vez interactivamente Obviamente el cálculo e; mucho mas com­plicado que para materiales clásicos. Se deberá 'Onecer a fondo el comportamiento onotropo de lo materiales compuestos para poder sacarles lodo su rendimiento.Las fibras se pueden obtener como fibras secas o como pre-im­pregnados. La fabricación con programados es la que mejores calidades ofrece.A pesar que para su almacenamiento son necesarias temperatura muy bajas y los ciclos de procesado son a alta temperatura y presión, es la forma más sencilla de la fabricación de materiales compuestos.

En general , la desventaja más clara de los materiales compuestos es el precio. Las características de los materiales y de los procesos encareceo mucho el producto. Para ciertas aplicaciones las bondades mecánicas como la alta rigidez específica (E/r).la buena estabilidad dimensional. la tolerancia a alta temperaturas. la resistencia a la corrosión, la ligereza o una mayor resistencia a la fatiga que los materiales clásicos compensan el alto precio.

Características
• Mejor resistencia a la fatiga
• Mejor rigidez
• Una mejor relación resistencia -peso
• Mayor resistencia a temperaturas elevadas
• Mayor resistencia.
• Mejor modulo de Young

Al igual que en el caso de los materiales compuestos particulados la regla de la mezcla dará siempre la densidad de los compuestos reforzados con fibra.

Si las fibras son continuas y unidireccionales, la regla predice con exac­titud la conductividad térmica y eléctrica

Cuando el esfuerzo aplicado es muy elevado la matriz casi no constitu­ye a la fibra del material, entonces:

Resistencia a la tensión de un material compuesto con libras continúas y paralelas

TS,= !, TS, +f.,a,.
TS,= resi>rencia a la tensión de la fibra
OM= esfuerzo que actúa sobre el material cuando las fibras se rompen

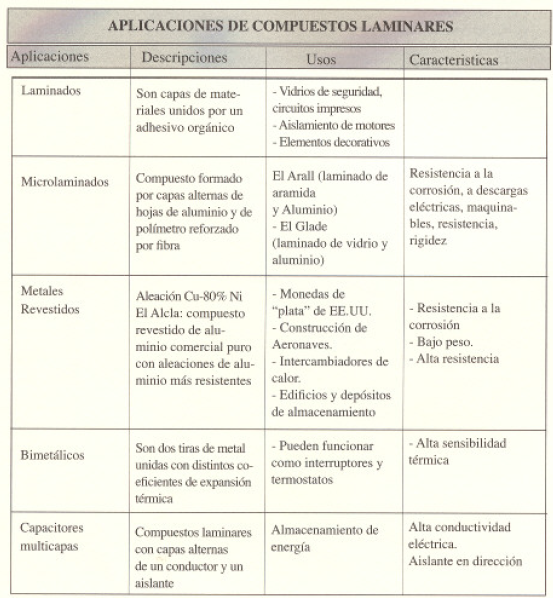
Materíalcs compuestos laminares

Caracterfsticas

• Mejorara la resistencia a la corrosión • Alta resistencia
• Resistencia superior al desgaste o la abrasión
• Expansión térmica poco usual
• Bajo costo.Bajo peso.Mejor apariencia

Regla de la mezcla

A partir de esta se puede determinar algunas propiedades de materiales compuestos laminares. calculadas con error despreciable.

Propiedades como la resistencia a la corrosión y al desgaste dependen principalmente de solo uno de los componentes del material compuesto. por lo que la regla de la mezcla no es aplicable.

Las propiedades en dirección paralela son:

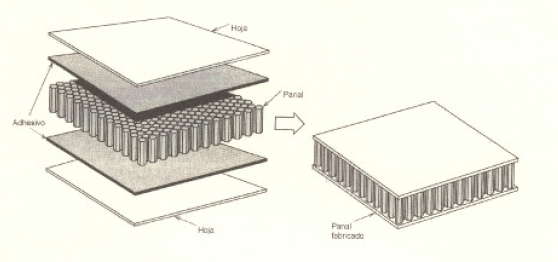
 Panal constituido por celdas hexagonales unidas a hojas mediante ca­pas adhesivas: produciendo estructuras ligeras. rígidas y resistentes.

Referencias

1. Anderson J.C., 2000, Ciencia de los Materiales, LIMUSA, México.

2. Askeland Donald R., Phule Pradeep P., 2004, Ciencia e Ingeniería de los Materiales, Thomson, EE.UU.

3. Balevsky, Angel, 1988, Metaloznanie, DURJAVNO IZDATELSTVO TECNICA, Bulgaria.

4. Buchkov D., 1980, Termichna Obrabotka na Metalite, Tekhnika, Bulgaria.

5. Callister jr. William D., 2003, Materials Science and Engineering an Introduction, John Wiley & Sons, Inc., EE.UU.

6. Jacobs James A., 2001, Experiments in Materials Science Engineering & Technology, Prentice Hall, EE.UU.

7. Kalpakjian Serope, 2001, Manufactura, Ingeniería y Tecnología, Prentice Hall, EE.UU.

8. Kamburov K, 1999, Materialoznanie, Izdadelstvo Varna, Bulgaria.

9. Mangonon Pat L., 2001, Ciencia de Materiales: Selección y Diseño, Prentice Hall, México. 563 Vesselina Radeva: Materiales compuestos reforzados con fibra.

10. Rusena Elena, 2004, Rukovodstvo za Laboratomi Upraznenia, Color Print, Bulgaria.

11. Schakelford James F., 2005, Introducción a la Ciencia de Materiales para Ingenieros, Pearson Prentice Hall, España.

12. Van Vlack Lawrence H., 1999, Materiales para Ingeniería, CECSA, México.