Introduccion
Como es conocido, el modelo CAPM (Capital Asset Pricing Model) es un modelo unifactorial que recoge la existencia de un unico factor explicativo de los rendimientos de los activos financieros al establecer que la rentabilidad esperada de un título es función lineal y positiva de su riesgo sistematico, medido este ultimo a traves de su coeficiente beta o sensibilidad de la rentabilidad del activo a los movimientos del mercado.
El CAPM, desarrollado inicialmente por Sharpe (1964), Lintner (1965) y Mossin (1966), analiza las implicaciones de la teoría de carteras eficientes en el equilibrio del mercado de capitales y establece que el inversor es remunerado exclusivamente por el riesgo sistematico. Por tanto, cuanto mas alto es el riesgo sistematico de un activo ode una cartera, mayor sera la rentabilidad que deberfa esperarse de la misma, poniendose de manifiesto que lo fundamental en la valoración de activos es el riesgo sistematico o riesgo de mercado, no siendo relevante el riesgo idiosincrasico o específico.
Este sencillo modelo de valoración, que trae consigo una simplificación de la realidad, tiene importantes limitaciones que diversos autores han intentado paliar durante años. En este sentido, se han relajado diversas hipotesis de partida 1 desarrollandose distintas extensiones del modelo. En este sentido destacamos la introduccion de la existencia de impuestos
[Brennan (1970), Elton y Gruber (1978), Litzenberger y Ramaswamy (1980), Constantinides (1983)], de costes de transacción [Brennan (1975), Goldsmith (1976), Stapleton y Subrahmanyam (1977), Levy (1978)], del fen6meno inflacionario [Lintner (1969) y Roll (1973), Chen y Boness (1975), Friend et al. (1976)], de un horizonte temporal multiperíodo [Stapleton y Subrahmanyam (1978), Merton (1973), Breeden (1979), Bergman (1985)] así como la relajación de la hipótesis del tipo de interes libre de riesgo [Brennan (1971) y Black (1972)].
A pesar de las limitaciones de este modelo de valoración de activos financieros, es evidente que el riesgo sistematico o coeficiente beta, aproximado como la covarianza entre la rentabilidad del activo y la de la cartera de mercado, se ha convertido en una importante herramienta para la toma de numerosas decisiones financieras. En este sentido, dicho coeficiente beta permite desarrollar estrategias de inversion y coste de capital, analizar coberturas de riesgo con activos derivados, gestionar y evaluar carteras, así como ser de utilidad en cualquier otra modalidad de analisis financiero donde se requiem una medida del riesgo. Por ello, el objetivo del presente trabajo de investigación es la contrastación empírica del modelo CAPM en el mercado bursatil español durante el período 1991-2000, con la finalidad de verificar si el riesgo sistematico es capaz de explicar las variaciones de rentabilidad de los distintos activos que cotizan en el mencionado mercado. Para alcanzar dicho objetivo, se efectua la estimación y contraste del modelo, utilizando la metodología propuesta por Fama y MacBeth (1973), para todo el horizonte temporal analizado, así como para los distintos meses del año, con la finalidad de observar si existe algun comportamiento estacional en la relación rentabilidad-riesgo.
El trabajo se estructura de la forma siguiente. Despues de esta introducción, en el epígrafe dos se efectua una breve descripción de los estudios empíricos del CAPM realizados en el mercado español. En el epígrafe tres se expone la muestra utilizada. En el epígrafe cuarto se describe la metodología. En el cinco se efectia la estimación y contraste del CAPM yen el siguiente epígrafe se lleva a cabo un analisis estacional de la prima de riesgo. Finalmente se exponen las conclusiones mas relevantes.
Evidencia empírica en el mercado español
En cuanto a los estudios realizados en el mercado bursatil español, hay que sefialar que uno de los primeros trabajos es el llevado a cabo por Palacios (1973), en el que nose observa una clara relación entre rentabilidad y riesgo, tal y como establece el CAPM. Otro trabajo importante es el de Berges (1984), en el que entre otros aspectos, se realiza la contrastación del CAPM utilizando datos mensuales de títulos pertenecientes a las balsas de Madrid, New York, Landres y Toronto. Entre sus principales conclusiones con respecto al mercado español, destaca que la distribución de las rentabilidades no se corresponde a una normal puesto que son mas asimetricas, los coeficientes beta no se mantienen estables durante el período objeto de estudio 1955-1981, y por ultimo, el coeficiente que acompañia a la beta resulta negativo pero no significativo a la hora de explicar las variaciones en la rentabilidad de los títulos españoles.
Tambien es destacable la contrastación del CAPM realizada por Rubio (1986,1988) en la cual se pone de manifiesto la no existencia de una relación de equilibria entre la rentabilidad y el riesgo para los distintos activos financieros. Dado que afirmar que el CAPM se satisface, es equivalente a argumentar que la cartera de mercado es eficiente en el sentido media-varianza, Rubio realiza un estudio sobre la eficiencia del índice ponderado por capitalización, rechazandose la eficiencia del mismo durante el período comprendido entre 1963 y 1982.
En el trabajo de Gómez-Bezares et al. (1994), en el cual se toman datos de rentabilidades semanales, mensuales y anuales, y mediante la utilización de distintas metodologías y tecnicas de estimación de los parametros, se contrasta el modelo de valoración en el mercado español durante el período 1959-1988 (Mercado de Corros) y 1990-1993 (Mercado Continuo). La contrastación en el primer período considerado pone de manifiesto que no se puede aceptar ni rechazar el modelo CAPM, mientras queen el segundo período, los resultados dependen de la metodología utilizada. Ademas se observa que se obtienen mejores resultados al utilizar la periodicidad anual que la mensual.
Corzo y Martinez-Abascal (1996) utilizan datos anuales de rentabilidades para la contrastación del modelo en el período 1988-1994. Los resultados de su trabajo son contrarios al CAPM ya que se pone de manifiesto la existencia de otros factores que influyen en las rentabilidades así como un premio por riesgo negativo. La existencia de una relación inversa entre riesgo y rentabilidad en los mercados bajistas son los resultados obtenidos por Corzo e Iglesias (1997) en el mercado bursatil español al realizar la contrastación del modelo con rentabilidades mensuales y anuales durante el período 1988- 1994. Dichas conclusiones son similares a las obtenidas por Grundy y Malkiel (1996) en el mercado estadounidense.
Marhuenda (1997) contrasta en su trabajo la existencia en el mercado bursatil español del efecto tamaño y de la estacionalidad utilizando carteras clasificadas por tamaño. Los resultados de su investigación muestran que las carteras de empresas pequefias presentan rentabilidades ajustadas al riesgo mayores que las grandes. Lo anterior pone de manifiesto que el CAPM no explica el comportamiento del mercado español. Otro de los trabajos que recoge la no influencia del riesgo sistematico en la rentabilidad de las acciones que cotizan en el mercado español, es el estudio de Gallego y Marhuenda
En cuanto a los estudios realizados en el mercado bursatil español, hay que sefialar que uno de los primeros trabajos es el llevado a cabo por Palacios (1973), en el que nose observa una clara relación entre rentabilidad y riesgo, tal y como establece el CAPM. Otro trabajo importante es el de Berges (1984), en el que entre otros aspectos, se realiza la contrastación del CAPM utilizando datos mensuales de títulos pertenecientes a las balsas de Madrid, New York, Landres y Toronto. Entre sus principales conclusiones con respecto al mercado español, destaca que la distribución de las rentabilidades no se corresponde a una normal puesto que son mas asimetricas, los coeficientes beta no se mantienen estables durante el período objeto de estudio 1955-1981, y por ultimo, el coeficiente que acompañia a la beta resulta negativo pero no significativo a la hora de explicar las variaciones en la rentabilidad de los títulos españoles.
Tambien es destacable la contrastación del CAPM realizada por Rubio (1986,1988) en la cual se pone de manifiesto la no existencia de una relación de equilibria entre la rentabilidad y el riesgo para los distintos activos financieros. Dado que afirmar que el CAPM se satisface, es equivalente a argumentar que la cartera de mercado es eficiente en el sentido media-varianza, Rubio realiza un estudio sobre la eficiencia del índice ponderado por capitalización, rechazandose la eficiencia del mismo durante el período comprendido entre 1963 y 1982.
En el trabajo de Gómez-Bezares et al. (1994), en el cual se toman datos de rentabilidades semanales, mensuales y anuales, y mediante la utilización de distintas metodologías y tecnicas de estimación de los parametros, se contrasta el modelo de valoración en el mercado español durante el período 1959-1988 (Mercado de Corros) y 1990-1993 (Mercado Continuo). La contrastación en el primer período considerado pone de manifiesto que no se puede aceptar ni rechazar el modelo CAPM, mientras queen el segundo período, los resultados dependen de la metodología utilizada. Ademas se observa que se obtienen mejores resultados al utilizar la periodicidad anual que la mensual.
Corzo y Martinez-Abascal (1996) utilizan datos anuales de rentabilidades para la contrastación del modelo en el período 1988-1994. Los resultados de su trabajo son contrarios al CAPM ya que se pone de manifiesto la existencia de otros factores que influyen en las rentabilidades así como un premio por riesgo negativo. La existencia de una relación inversa entre riesgo y rentabilidad en los mercados bajistas son los resultados obtenidos por Corzo e Iglesias (1997) en el mercado bursatil español al realizar la contrastación del modelo con rentabilidades mensuales y anuales durante el período 1988- 1994. Dichas conclusiones son similares a las obtenidas por Grundy y Malkiel (1996) en el mercado estadounidense.
Marhuenda (1997) contrasta en su trabajo la existencia en el mercado bursatil español del efecto tamaño y de la estacionalidad utilizando carteras clasificadas por tamaño. Los resultados de su investigación muestran que las carteras de empresas pequeñas presentan rentabilidades ajustadas al riesgo mayores que las grandes. Lo anterior pone de manifiesto que el CAPM no explica el comportamiento del mercado español. Otro de los trabajos que recoge la no influencia del riesgo sistematico en la rentabilidad de las acciones que cotizan en el mercado español, es el estudio de Gallego y Marhuenda.
(1997), utilizando para ello rentabilidades mensuales duran te el horizonte temporal comprendido entre 1963 y 1990. Si bien introducen en el modelo la /32 , la desviación típica y la coasimetría, estas variables carecen de poder explicativo en el comportamiento de la rentabilidad. El analisis del CAPM que realiza Nieto (2001) en el mercado español durante el período 1987-1998 muestra resultados que no son favorables a la relación establecida en el CAPM al obtener primas por riesgo no significativas e incluso llegando a ser negativas. Ademas obtiene evidencia de la estacionalidad en el mes de enero, al obtener primas por riesgo superiores en dicho mes con respecto a los restantes meses del año. Nieto y Rubio (2002), para el mismo período temporal, llevan a cabo una nueva especificación del coeficiente beta, que recoge multiples factores de riesgo sistematico, pero los resultados obtenidos en el estudio empírico no permiten aceptar el cumplimiento del modelo.
3. La muestra objeto de investigación
Los datos utilizados en nuestro trabajo de investigación estan formados por rentabilidades instantaneas mensuales 2, ajustadas por splits y ampliaciones de capital, de acciones que han cotizado en el mercado bursatil español durante el período comprendido entre diciembre de 1990 y diciembre de 2000. Con dicha base de datos construimos dos muestras, una de activos individuales y otra de carteras por tamaño. Como cartera de mercado se toman distintas aproximaciones, utilizandose tres indices bursatiles: el Indice General de la Bolsa de Madrid (IGBM)3, un índice equiponderado y un índice ponderado por capitalización, construyendose los dos ultimos tanto para la muestra de activos individuales como para la de carteras por tamaño.
Para la selección de ambas muestras, partimos inicialmente de la totalidad de activos que cotizan en el mercado a 31 de diciembre de 2000. La muestra de títulos individuales esta constituida por todos los activos que han cotizado en mas del 75% de las sesiones diarias correspondientes a cada uno de los diez años de inv estigación4 En cambio, a los títulos pertenecientes a la muestra de carteras por tamaño no se les ha exigido ningun requisito de frecuencia de contratación, siendo seleccionados un total de 141 títulos 5• Podemos considerar que los títulos individuales seleccionados constituyen una muestra representativa del mercado continua español puesto que en la misma se incluyen la totalidad de los sectores, segun la clasificación establecida por la Bolsa de Madrid y vigente a 31 de diciembre de 2000. En este sentido, los sectores que tienen mayor peso en la muestra son los de Bancos-Financieras, Metal-Mecanica y Otras Industrias y Servicios, representando el primero de ellos el 23,3% del total y los dos restantes el 13,3%, situandose el sector de Construcción en el I L7%. A su vez, tambien destacan los sectores de Electricas, Alimentación y Petróleo-Química al presentar cada uno de ellos una importancia relativa del 10%.
Con respecto a la construcción de las carteras por tamaño es preciso sefialar que, una vez obtenido el valor de mercado o capitalización bursatil de todos los activos en cada uno de los meses, se clasifican segun la capitalización del mes anterior, de mayor a menor, repartiendose posteriormente en diez carteras. Por consiguiente, la cartera 1 esta constituida exclusivamente por las empresas de mayor tamaño o capitalización, mientras que la cartera l O contiene las empresas de la muestra con menor dimension o tamaño.
El procedimiento utilizado para determinar la rentabilidad instantanea de cada una de las carteras se describe a continuación. En primer lugar se calcula para cada uno de los meses la rentabilidad simple de la cartera, como la media aritmetica de las rentabilidades de los distintos activos que constituyen la misma. A continuación, la rentabilidad instantanea de cada cartera r[lt se obtiene a partir de la correspondiente simple, utilizando para ello la siguiente ecuación que recoge la equivalencia financiera entre ambas rentabilidades: r = log ( I + R ), siendo R la rentabilidad simple de una cartera en el mes t6 •
Para la elaboración de las rentabilidades continuas del indice equiponderado y del ponderado se han utilizado las rentabilidades de todos los activos disponibles en cada muestra, 60 para la de títulos individuales y 141 para la de carteras. El procedimiento seguido para su calculo es similar al descrito para las carteras.
Por ultimo, es importante señalar que la información relativa a los dividendos, ampliaciones de capital gratuitas, el valor teórico de los derechos de suscripción y splits correspondientes a los distintos títulos, ha sido obtenida a partir de los lnformes Anuales de la Bolsa de Madrid referentes al período de estudio y de la información suministrada por dicha Bolsa a traves de su pagina web en internet7.
4. Metodología de contraste
Tai y como se ha expuesto, el modelo de valoración con cartera de mercado establece una relación lineal y positiva entre la rentabilidad de un activo o cartera y su riesgo beta. Siendo la expresión matematica del modelo CAPM:

A la hora de contrastar este modelo de valoración existen dos metodologías distintas, la de serie temporal y la de corte transversal. La metodología de serie temporal consiste en contrastar el modelo para cada uno de los activos o carteras a lo largo del horizonte temporal, mientras que la metodología de corte transversal se caracteriza por la contrastación del modelo en un determinado período y para el conjunto de activos o carteras disponibles. Dentro de esta modalidad nos encontramos con el contraste de corte transversal con medias y el contraste de corte transversal sin medias, siendo esta ultima la metodología clasica en la contrastacion del modelo de valoracion de activos CAPM.
Este contraste de corte transversal sin medias propuesto por Fama y MacBeth (1973) y utilizado, entre otros por Litzenberger y Ramaswamy (1979), Gomez-Bezares et al. (1994) y Nieto (2002), consta de dos etapas. La primera de ellas consiste en estimar el riesgo o coeficiente beta de los distintos activos o carteras, mediante el Modelo de Mercado, en cada uno de los T períodos, utilizando los datos de rentabilidad correspondientes a 60 meses anteriores. La regresion lineal para cada activo o cartera es la siguiente:
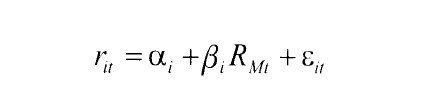
En segundo lugar, Fama y MacBeth proponen realizar una regresion de sección cruzada, mediante la tecnica de MCO y para cada momenta del tiempo, siendo la variable explicativa, los coeficientes beta estimados en la etapa anterior y la variable endogena las rentabilidades de los distintos activos. 0 sea, realizar T regresiones con N observaciones, las cuales corresponden a los T activos disponibles. La expresion matematica de dicha regresion es:

Una vez realizadas las T regresiones cross-sectional, obtenemos dos series de estimadores Yor y Y,r· Si asumimos que las rentabilidades de los distintos activos y carteras son normales, independientes e identicamente distribuidas, los mencionados estimadores tambien lo seran, por lo que se puede contrastar el modelo CAPM, mediante la siguiente prueba de hipotesis de significacion individual:

Ya que para la aceptacion del modelo de valoración, segun la version cero-beta de Black 8, se debe cumplir que y0 y y1 sean significativos y tomen valores positivos. El estadístico y de prueba es:

Siendo:
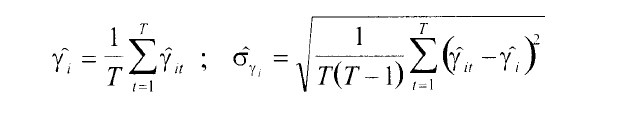
El estadístico anterior sigue una distribucion t de Student con (T - 1) grados de libertad, por lo que se rechaza la hipótesis nula si t(Y1)> t r 1 x 1.a • En el caso de disponer de muestras grandes (T > 30), el mencionado estadístico de contraste sigue una distribucion normal con media 0 y varianza 1, de manera que sera necesario que t(f 1)> z,, para rechazar la hipótesis nula.
En este contraste de corte transversal sin medias tambien se presentan problemas econometricos 10 referentes a las perturbaciones por lo que los estimadores y y y11 son ineficientes, solucionandose estos problemas mediante de la utilización de la tecnica de Mínimos Cuadrados Generalizados (MCG), al establecer un supuesto sobre la estructura del comportamiento de la matriz de varianzas y covarianzas de la perturbación aleatoria No obstante, tal y como establecen Marín y Rubio (2001 ), la matriz de varianzas y covarianzas de las perturbaciones aleatorias no se encuentra recogida en la expresión que nos permite obtener el estadístico t por lo que quedan resueltos los problemas econometricos referentes a la heterocedasticidad que sf estaban presentes en la regresión unica del corte transversal con medias.
Al tomar estimaciones del riesgo beta, y no sus verdaderos valores en la regresión de sección cruzada, siguen existiendo problemas de errores en las variables, por lo que las estimaciones de Yor y y 11 son inconsistentes. Siguiendo a Marín y Rubio (2001 ), una manera de solucionar este problema es mediante el ajuste que propane Shanken (1996) y que consiste en multiplicar la varianza de los estimadores c\ por un determinado factor de ajuste 12• La expresión analitica del mencionado factor de ajuste es:
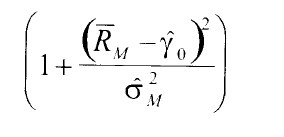
Siendo:

Estimación y contraste del CAPM
En el presente epígrafe vamos a efectuar la contrastación empírica del modelo CAPM para el horizonte temporal total, que abarca desde el 31 de diciembre de 1990 hasta el 31 de diciembre de 2000, utilizando la metodología de corte transversal sin medias.
En la primera etapa de la metodología propuesta por Fama y MacBeth (1973) hay que estimar, en cada uno de los meses del período muestral, los coeficientes beta de los 60 activos, utilizando la tecnica de Mfnimos Cuadrados Ordinarios (MCO). Para la estimación de dicho riesgo beta a traves del Modelo de Mercado, se utilizan los datos de rentabilidad de 60 meses anteriores, por lo que la primera estimación realizada corresponde al mes de enero de 1996, la segunda corresponde a febrero de 1996, y así sucesivamente, hasta llegar a diciembre de 2000.
Una vez llevada a cabo la primera etapa del contraste de Fama y MacBeth, se efectua la segunda, que consiste en regresion de seccion cruzada entre las rentabilidades de los distintos activos o carteras y los coeficientes beta previamente estimados en la etapa anterior. La ecuacion de regresion crosssectional es la siguiente:
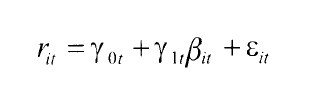
Dicha regres1on, que tiene como finalidad contrastar la existencia de una relacion lineal y positiva entre la rentabilidad de un activo o cartera y su riesgo beta, ha de realizarse en cada uno de los 60 meses comprendidos entre enero de 1996 y diciembre de 2000. Una vez obtenidas los coeficientes y0t y y1t para cada uno de los activos y carteras, se realiza el contraste de significatividad individual de los estimadores con la finalidad de verificar si se cumplen las implicaciones del CAPM. Para la aceptacion de las hipotesis del modelo vamos a utilizar la version cero-beta de Black, menos restrictiva que la de Sharpe-Lintner, en la que solo es necesario verificar que ambos parametros tomen valores positivos y que sean estadísticamente significativos.
En las tablas 1 y 2 se recogen los resultados rnedios del rnencionado contraste para los títulos individuales y para las carteras por tarnaño, respectivamente. En la rnisma se muestran el valor medio de los estirnadores, su error estandar, el estadístico t y su correspondiente p-valor. Adernas, se ha realizado el ajuste propuesto por Shanken (1996) para elirninar el problerna del error de estimacion, por lo que se presentan los valores ajustados. En la tabla 1 se observa que, sin corregir los errores en la estirnacion, el parametro y es positivo y estadísticamente significativo con independencia del índice bursatil utilizado. En cuanto a la prirna por riesgo, que viene representada por el parametro y , resulta ser considerablemente pequeña, negativa 1 y no significativa, independientemente de que el índice utilizado como proxy de la cartera de mercado sea el IGBM, el equiponderado o el ponderado por capitalización. Ademas, se observa que los valores de la prima por riesgo son mas pequefios al tomar el índice equiponderado, siendo mayores al considerar el índice ponderado. Al aplicar el ajuste propuesto por Shanken, se obtienen identicos resultados, primas negativas y no significativas, por lo que se ha puesto de manifiesto que no existe una relación lineal y positiva entre el rendimiento esperado de los activos y su riesgo beta, no cumpliendose el modelo de valoración CAPM para el conjunto de títulos analizados en el período 1991-2000.
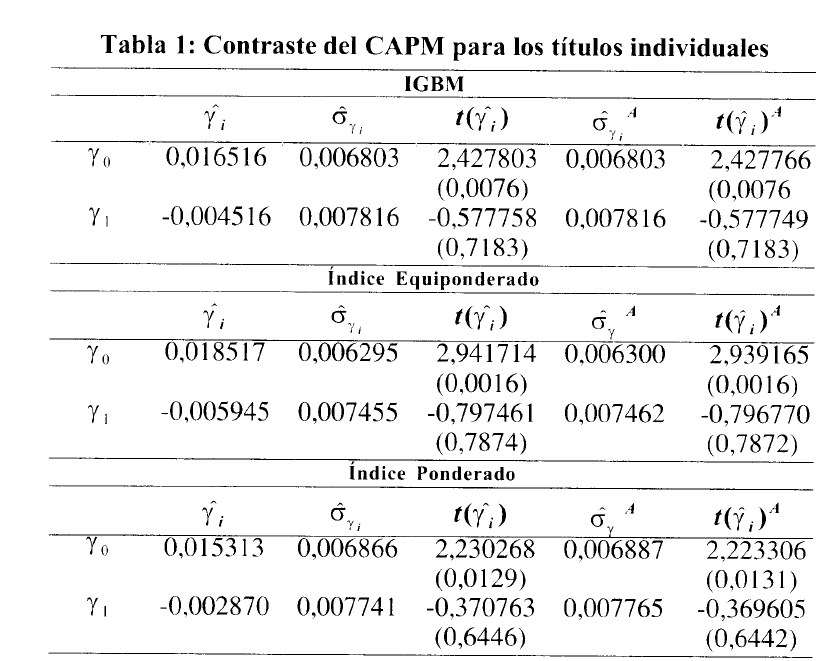
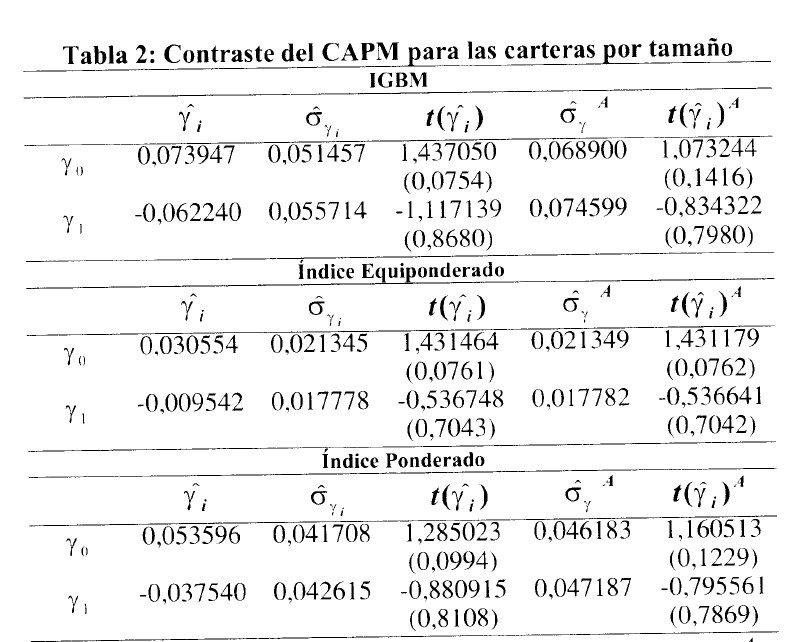
Al construir carteras por tamaño (tabla 2), los resultados del contraste muestran que para los tres índices de mercado, la ordenada en el origen y0 es positiva mientras que la pendiente o prima por riesgo es negativa, no siendo ambos parametros significativos estadísticamente al considerar un error alfa del 5%. Si aumentamos el nivel de significación al 10%, la ordenada en el origen resulta significativa con todos los índices de mercado. Dichos resultados se obtienen al utilizar como proxy de la cartera de mercado el IGBM, el índice equiponderado y el ponderado por capitalización. Al corregir los errores en las variables, los resultados son identicos a los comentados anteriormente.
Ademas, se observa tambien que el índice equiponderado es el que proporciona una mayor prima de riesgo, obteniendose los valores mas pequefios al tomar el IGBM. Tenemos pues, que al tomar carteras por tamaño, las implicaciones del CAPM en el mercado español tampoco se cumplen.
Una sfntesis de la contrastación empírica del modelo CAPM en el mercado español, utilizando las tres proxys de la cartera de mercado y tomando como variable dependiente las rentabilidades instantaneas de t{tulos individuales y de carteras de activos construidas por tamaño se recoge en la tabla 3.
Tenemos, pues, que, con independencia de disponer de titulos ode carteras, las primas por riesgo no son significativas y presentan valores negativos. Con respecto a la ordenada en el origen, con cualquiera de las muestras e indices utilizados esta toma siempre valores positivos, siendo significativa al 5% y al 10% en la mayoría de los casos. Teniendo en cuenta lo expuesto, no se puede aceptar el cumplimiento del modelo CAPM en el mercado español durante el periodo 1991-2000 en ninguna de las muestras analizadas.

Estos resultados alcanzados para el período 1991-2000 coinciden con los obtenidos por otros autores en el mercado español, si bien estos realizan sus contrastes empíricos en intervalos temporales distintos. As{ por ejemplo, destacamos a Palacios (1973), Berges (1984), Rubio (1986, 1988), Gallego et al. (1992), Basarrate y Rubio (1994), Sentana (1995) y Nieto (2002) en los que se rechaza la relación lineal y positiva entre la rentabilidad esperada del activo y su riesgo beta, establecida por el modelo de valoración de activos financieros con cartera de mercado.
6. Una aproximación al comportamiento estacional de la prima de riesgo
La estimación y contraste del CAPM ha puesto de manifiesto el incumplimiento de este modelo en el mercado bursatil español durante el período 1991-2000, indicando la inexistencia de una relación positiva entre la rentabilidad y riesgo sistematico de los activos y carteras por tamaño. No obstante, en diversos trabajos realizados en el mercado español de capitales, como el de Rubio (1986) y Marhuenda (1998) para los períodos 1963-1982 y 1963-1989, respectivamente, se rechaza el modelo CAPM globalmente pero se obtuvieron relaciones positivas y significativas entre el riesgo beta y la rentabilidad de los títulos individuales en el mes de enero. Estos resultados ponen de relieve que los inversores tinicamente han sido recompensados por soportar el riesgo asumido en dicho mes. Por consiguiente, y con la finalidad de verificar si este comportamiento estacional en la relación entre rentabilidad y riesgo sigue estando presente en nuestro mercado durante el período 1991-2000, vamos a efectuar en este ep{grafe un estudio empírico de la estacionalidad de la prima de riesgo de los títulos individuales y de las carteras por tamaño.
En primer Iugar, y con las series y y y11 obtenidas tras Ia estimación y contraste del CAPM, efectuada en el epígrafe anterior mediante la utilización de la metodología de Fama y MacBeth (1973), se van a realizar los contrastes de significación estadística de las mencionadas series de estimaciones diferenciando dos grupos distintos. Por un lado, se recogen exclusivamente los estimadores obtenidos en el mes de enero, y por otro, se encuentran los correspondientes a Ios restantes meses del año. Esta diferenciación en dos grupos se Ileva a cabo para verificar si Ia prima de riesgo correspondiente al mes de enero difiere de las alcanzadas en los demas meses del año. Los resultados medios del contraste de significatividad, tanto para el mes de enero como para los restantes meses, se recogen en las tablas 4 y 5 para los títulos individuales y las carteras por tamaño, respecti vamente.
Los resultados medios de los títulos individuales nos indican que Ia prima por riesgo del mes de enero es positiva con cualquiera de los tres indices utilizados como proxys de la cartera de mercado, siendo significativa la obtenida con el índice equiponderado si tomamos un error alfa del 5%, mientras que si este error aumenta al 10%, tambien resulta significativa para los restantes indices bursatiles. En este sentido, de los tres indices que se disponen, el indice equiponderado es el que proporciona una mayor prima. La ordenada en el origen obtenida en los meses de enero toma un valor medio positivo con el IGBM y el indice ponderado por capitalización, presentando un valor negativo con el equiponderado, no siendo relevante en ninguno de los tres modelos. Con respecto a Ios restantes meses del año, la prima por riesgo no es positiva, como ocurre en el mes de enero, sino que toma valores negativos, no siendo significativa con ninguno de los tres indices bursatiles. La ordenada en el origen al utilizar cualquiera de los indices de mercado, es positiva y significativa al considerar un error del 5%.

Con respecto a los resultados que se obtienen al construir carteras por tamaño, se observa que los mismos difieren de los obtenidos con la muestra de títulos individuales. En este sentido, hay que destacar que la prima de riesgo es negativa en los meses de enero, no siendo significativa con ninguno de los indices de mercado, mientras que la ordenada en el origen toma valores positivos y no resulta ser estadísticamente significativa. Estos resultados se obtienen con los tres indices bursatiles utilizados como proxys de la cartera de mercado.

En cuanto a los restantes meses del año, la prima por riesgo sigue siendo negativa al tomar el IGBM y el índice ponderado por capitalización, tomando un valor positivo con el índice equiponderado, no siendo significativa en ninguno de los tres casos al considerar un error alfa del 5%. La ordenada en el origen, resulta positiva y significativa con independencia del índice bursatil utilizado como proxy de la cartera de mercado.
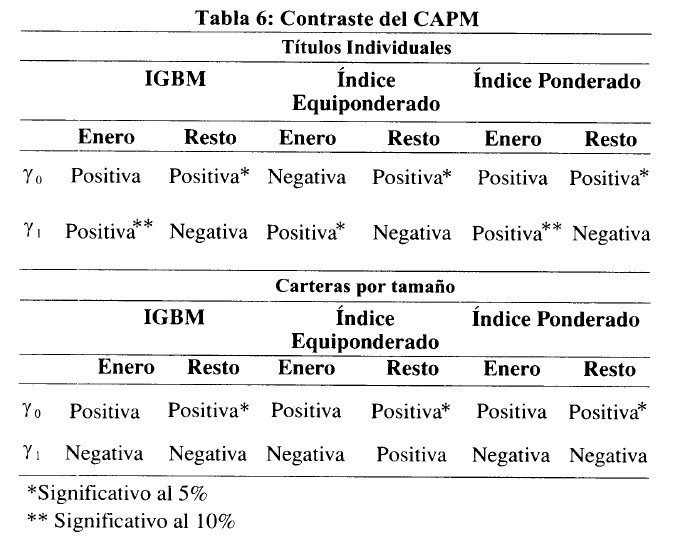
Considerando los resultados expuestos, se puede afirmar que para el conjunto de activos individuales, la relación existente entre rentabilidad y riesgo en el mes de enero es positiva y significativa, mientras que para los restantes meses del año, su valor es negativo y no resulta significativa. Con respecto a la muestra de carteras, hay que destacar que todas las primas de riesgo no son significativas, siendo mayoritariamente negativas. Un resumen de lo expuesto se recoge en la tabla 6.
Puesto que los resultados de la estimación y contraste de las primas por riesgo de los activos individuales en el mes de enero, han resultado ser distintos a los obtenidos al considerar la totalidad de los meses del año, hemos considerado oportuno determinar las primas correspondientes a cada uno de los meses del año. Dichas primas se van a calcular tanto para los títulos individuales como para la muestra de carteras por tamaño, complementando así el analisis estacional de la prima por riesgo.
Una vez obtenida la prima por riesgo en cada uno de los meses, y con las series de estimaciones y Ir' se realiza el contraste de significación estadística de los mismos, utilizando como cartera de mercado el IGBM y los dos índices construidos. Los resultados, que se muestran en las tablas 7 y 8, recogen el promedio de los estimadores mensuales así como el estadístico t ajustado correspondientes a los distintos t{tulos analizados.

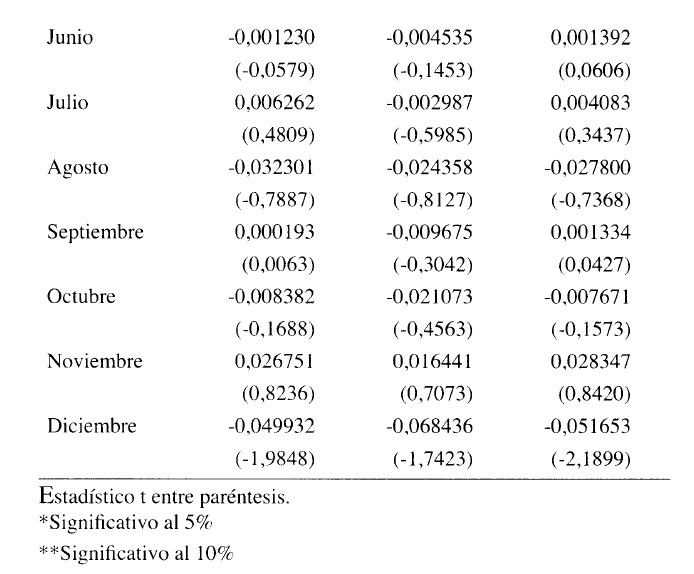
Los valores que toma la prima por riesgo en cada uno de los meses del año para los distintos activos considerados individualmente, tal y como se expone en la tabla 7, muestran que la prima de mayor cuantfa corresponde al mes de noviembre, al utilizar el IGBM y el índice ponderado por capitalización como proxys de la cartera de mercado, mientras que es superior en el mes de enero al considerar el índice equiponderado. Con respecto al signo que toman las distintas primas por riesgo, se observa que, independientemente del índice utilizado, los meses de febrero y noviembre presentan una prima positiva, mientras que los meses de abril, mayo, agosto, octubre y diciembre toman valores negativos. En los restantes meses, las primas toman signos positivos o negativos en función del índice de mercado. La prima de riesgo correspondiente al mes de enero es la unica que ha resultado positiva y significativa.

Al llevar a cabo el contraste de significación estadística de la prima de riesgo en cada uno de los meses del año para las carteras (tabla 8) se observa que al utilizar el IGBM como cartera de mercado, el mes de marzo es el que proporciona un mayor premio por riesgo, siendo superior el del mes de abril al considerar el índice equiponderado y ponderado por capitalización. Si bien al realizar el contraste para todos los meses del año, a excepción del mes de enero, se ponfa de manifiesto que la prima era negativa y no significativa al tomar como índice de mercado el IGBM y el ponderado por capitalización, al analizar las primas de riesgo mes a mes, se observa que son positivas en los meses de marzo y abril con independencia del índice bursatil utilizado. Con respecto al mes de abril, hay que sefialar que la prima es significativa al 5% cuando se utiliza el índice equiponderado, si aumentamos el error alfa al 10%, tambien resulta significativa la prima de dicho mes al considerar el índice ponderado como cartera de mercado. Los meses de enero, junio, julio, agosto y diciembre presentan primas negativas, mientras que en los restantes meses las primas toman valores positivos y negativos en función de la aproximación de la cartera de mercado que se tome.
Conclusiones
El objetivo del presente trabajo de investigación ha sido analizar la influencia del riesgo sistematico o riesgo de mercado en las variaciones de la rentabilidad de los distintos activos y carteras del mercado bursatil español. Por ello se ha efectuado la estimación y contraste del modelo CAPM utilizando la metodología de corte transversal sin medias propuesta por Fama y MacBeth (1973). Las estimaciones de las primas por riesgo obtenidas para el período 1991-2000 no han resultado significativas en ninguna de las muestras utilizadas, tanto al tomar títulos individualmente como carteras de activos, y con independencia del índice bursatil tornado como proxy de la cartera de mercado. Dichos resultados ponen de manifiesto la inexistencia de una relación lineal, positiva y significativa entre la rentabilidad esperada del activo o cartera y su riesgo sistematico, por lo que no se verifica el cumplimiento del modelo CAPM en el mercado español para la muestra y período temporal analizado.
La estimación y contraste del modelo tambien se ha efectuado en el mes de enero y en los restantes meses del año con la finalidad de analizar la posible estacionalidad de la prima por riesgo de los títulos y carteras en el mercado español. Los resultados obtenidos en la muestra de activos individuales indican que la prima por riesgo es positiva y significativa en el mes de enero, mientras queen el resto de los meses la prima es negativa y no significativa. Con respecto a las carteras, las primas de riesgo correspondientes al mes de enero no han resultado significativas, tomando un valor medio negativo. En los restantes meses del año, la prima por riesgo es mayoritariamente negativa, observandose la existencia de una prima positiva y significativa en el mes de abril para la muestra de carteras por tamaño, cuando se toma los dos índices construidos.
En sfntesis, al efectuar la contrastación del modelo CAPM globalmente, se obtiene que el riesgo sistematico o riesgo de mercado no influye en las variaciones de rentabilidad de los títulos españoles, pero s{ se ha obtenido evidencia empírica de la influencia positiva y significativa de dicho riesgo en el mes de enero para los títulos individuales y en el mes de abril para las carteras por tamaño. De cualquier forma, queda puesto de manifiesto que el riesgo sistematico no constituye un buen predictor de las rentabilidades futuras en el mercado bursatil español.
Bibliografia
BASARRATE, B. (1988): "El efecto tamaño y la imposición sobre dividendos y ganancias de capital". lnvestigaciones económicas, vol. 2, n° 2, 225-242.
BASARRATE, B. y G. RUBIO (1994): "La imposición sobre plusvalfas y minusvalfas: sus efectos sobre el comportamiento estacional del mercado de valores". Revista Española de Economta, vol. 11, pp. 246-277.
BERGES, A. (1984): El mercado español de capita/es en un contexto internacional. Ministerio de Economfa y Hacienda, Madrid.
BERGMAN, Y. Z. (1985): "Time preference and capital asset pricing models". Journal of Financial Economics, vol. 14, n° 1, marzo, pp. 145 BLACK, F. ( 1972): "Capital market equilibrium with restricted bo rrowing". Journal of Business, vol. 45, n° 3, julio, pp. 444-455.
BOLSA DE MADRID: lnformes Anuales. Anos 1991-2000. Madrid.
BREEDEN, D.T. (1979): "An intertemporal asset pricing model with stochastic consumption and investment opportunities", Journal of Financial Economics, 7, pp. 265-269.
BRENNAN, M. (1970): "Taxes, market valuation and corporate financial policy". National Tax Journal, vol. 23, n° 4, diciembre, pp. 417-427.
BRENNAN, M. (1971): "Capital market equilibrium with divergent borrowing and lending rates". Journal of Financial and Quantitative Analysis, vol. 6, diciembre, pp. 1197-1205.
BRENNAN, M. (1975): "The optimal number of securities in a risk asset portfolio when there are fixed costs of transacting: theory and some empirical results". Journal of Financial and Quantitative Analysis, 10, pp. 483-496.
CHEN, A.H. y A.J. BONESS (1975): "Effects of uncertain inflation on the investment and financing decisions of a firm". Journal of Finance, vol. 30, n° 2, pp. 469-483.
CONSTANTINIDES, G. (1983): "Optimal stock trading with personal tax". Econometrica, 51, pp. 611-636.
CORZO, T. y S. IGLESIAS (1997): "Beta como medida del riesgo en mercados bajistas: una aplicación a la Balsa de Madrid". V Faro de Finanzas, Asociación Espanola de Finanzas (AEFIN). Universidad de Malaga, pp. 575-587.
CORZO, T. y E. MARTINEZ-ABASCAL (1996): "Anomalias en lava loración de activos y CAPM en la Bolsa de Madrid: 1988-1994". IV Faro de Finanzas, Asociación Espanola de Finanzas (AEFIN). Madrid, pp. 373-.
ELTON, E.J. y M.J. GRUBER (1978): "Taxes and portfolio composition". Journal of Financial Economics, 6, pp. 399-410.
FAMA, E.F. y J.D. MACBETH (1973): "Risk, return and equilibrium: empirical tests''. Journal of Political Economy, 81, pp. 607-636.
FRIEND, I., Y. LANDSKRONER y E. LOSQ ( 1976): "The demand for risky assets under uncertain inflaction". Journal of Financial, vol. 31, diciembre, pp. 1287-1297.
GALLEGO, A., J.C. GOMEZ y J. MARHUENDA (1992): "Evidencias empíricas del CAPM en el mercado espanol de capitales". Instituto Valenciano de Investigaciones económicas, WP-EC 92-13.
GALLEGO, M.A. y J. MARHUENDA (1997): "Riesgo sistematico, total y coasimetria en la valoración de activos". Revista fapañola de Financiación y Contabilidad, vol. 26, n° 90, pp. 145-165 GOLDSMITH, D. ( 1976): "Transactions costs and the theory of portfolio selection". Journal of Finance, vol. 31, n° 4, septiembre, pp. 1127-1139.
GOMEZ-BEZARES, F., J.A MADARIAGA y J. SANTIBANEZ (1994): Valoración de acciones en la Bolsa Espanola. Biblioteca de Gestión, Ed. Desclee de Brouwer. Bilbao.
GRUNDY, K. y B.G. MALKIEL (1996): ''Reports of beta's death have been greatly exaggerated". Journal of Portfolio Management, primavera, pp. 36-44.
LEVY, H. (1978): "Equilibrium in an imperfect market: a constraint on the number of securities in a portfolio''. American Economic Review, 68, pp. 643-658.
LINTNER, J. (1969): "The aggregation of investor's diverse judgments and preferences in purely competitive security markets". Journal of Financial and Quantitative Analysis, 4, pp. 347-400.
LITZENBERGER, R.H. y K. RAMASWAMY (1980): "Dividends, short selling restrictions, tax-induced investor clienteles and market equilibrium". Journal of Finance, 35, pp. 469-482.
MARHUENDA, J. ( 1997): Anomal{as en los modelos de valoración de activos. Universidad de Alicante, Secretariado de Publicaciones.
MARKOWITZ, H. (1952): Portfolio selection. The Journal of Finance, marzo, pp. 77-91.
MERTON, R. (1973): "An intertemporal asset pricing model", Econometrica, 41, pp. 867-887.
NIETO, B. (2001): "Los modelos multifactoriales de valoración de activos: un analisis empírico comparativo". IX Foro de Finan::,as, Asociación Espanola de Finanzas (AEFIN). Universidad Publica de Navarra.
NIETO, B y G. RUBIO (2002): "El modelo de valoración con cartera de mercado: una nueva especificación". Revista fapañola de Financiación y Contabilidad, vol. 31, n° 113, pp. 697-723.
NEWEY, W. y K. WEST (1987):"A simple, positive definite, heterocedasticity and autocorrelation consistent covariance matrix". Econometrica, 55, 703-708.
PALACIOS, J. (1973): The stock market in Spain: Tests of efficiency and capital market theory. Tesis doctoral no publicada, Standford University.
ROLL, R. (1973): "Assets, money and commodity price inflation under uncertainty". Journal of Money, Credit and Banking, noviembre, vol. 5, n°4, pp. 905-923.
RUBIO, G. (1986): "Analisis multivariante del cero-beta CAPM: el mercado español de capitales". Revista Espanola de Econom(a, n° 3, pp. 344-365.
RUBIO, G. (1988): "Further international evidence on asset pricing: The case of the Spanish capital market". Journal of Banking and Finance, 12,pp. 221-242
RUBIO, G. (1995): "Further evidence on períormance evaluation: portfolio holdings, recommendations and turnover costs". Journal of Quantitative Finance and Accounting, n° 5, pp. 127-153.
SENTANA, E. (1995): "Riesgo y rentabilidad en el mercado español de valores". Moneda y Credito, vol. 200, pp. 133-167.
SHANKEN, J. (1992): "On the estimation of beta-pricing models". Re view of Financial Studies, 5, pp. 1-34.
SHANKEN, J. (1996): "Statistical methods in tests of portfolio efficiency: A synthesis". En Handbook of Statistics, vol. 14, Eds. S. Maddala y C. Rao, Elsevier Sciencies.
SHARPE, W.F. ( 1964): "Capital asset prices: a theory of market equilibrium under conditions of risk". The Journal of Finance, vol. 19, n° 3, pp. 425-442.
STAPLETON, R. y M. SUBRAHMANYAM (1977): "Market imperfections, capital market equilibrium and corporate finance". Journal of Finance, 32, pp. 307-319.
STAPLETON, R. y M. SUBRAHAMANYAM (1978): "A multiperiod equilibrium asset pricing model". Econometrica, vol. 46, n° 5, septiembre, pp. 1077-1096.
