Introducción

Sea la ecuación de Schrodinger para una partícula libre en una dimensión:

 El problema de resolución exacta de esta ecuación y el es­tudio de su simetría fue planteado y estudiado durante varios decenios: véase [1, 2] y su bibliografía, nuestros artículos [3, 4], etc. Por ejemplo, fueron construidos los operadores de simetría hacia segundo orden y encontradas las soluciones in­teresantes [5]. El problema de clasificación de los operadores de simetría (las primeras integrales de movimiento) para una partícula cuántica fue planteado en nuestro articulo [6] y de­sarrollado en [4].

En este articulo presentamos el estudio sistemático de la clasificación de los operadores de simetría hacia tercer orden , encontramos los resultados nuevos y ordenamos, precisamos y corregimos los resultados conocidos.

1. Las transformaciones de equivalencia

Planteamos el problema de las transformaciones que no va­ rían la estructura de la ecuación (1). Aplicándole a la ecuación (1) la transformación siguiente: 

Notamos que v 4 representa la transformación idéntica y v 2 describe la reflexión de la coordenada x y a la multi­plicación simultanea de la función de onda por -i . Es fácil verificar que la ecuación (1 ) se transforma en cada caso de la manera siguiente:

Las mencionadas transformaciones se conocen en la li­ teratura [ 1-3], pero tal representación sistemática es nueva.

Usando el grupo total de transformaciones de equivalencia G (r) N podemos realizar la clasificación de los operadores de simetría.

2. Clasificación de los operadores de simetría del primer orden

Usando la condición de conmutación con el operador de la ecuación (1): [ Á , B ] = 0 buscamos los operadores lineales con respecto al momento:

Aquí el operador de simetría B₁ corresponde a la ley de conservación del momento lineal y el operador 2 a la con­servación de la coordenada inicial. El operador 3 es ope­rador trivial : es evidente que cualquier constante está en con- 30 mutación con un operador lineal. Estudiamos ahora la trans­formación de estos operadores generada por cada subgrupo de equivalencia:

Concluimos que si en (5 a) n t. O , entonces por la elección t 0 = mina y nx 0 = -r siempre es posible eliminar los términos con B B 3 • Si n = O entonces se queda sólo el operador B: el término con B.1 se elimino por la elección de la constante p. Entonces el subgrupo G permite reducir todo conjunto de los operadores de tipo (5 a) a sólo dos cla­ses, cuyos representantes más sencillos son B2 y B1 (aquí despreciamos los primas en los operadores). Vamos a ver que estas clases son equivalentes relacionadas con las transforma­ciones del subgrupo N.

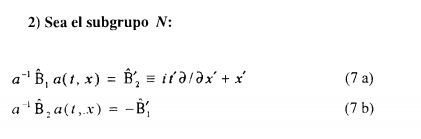
El hecho de que el subgrupo de equivalencia (4 a) y (4 b) transfonna mutuamente B 1 en B2 y viceversa, está demos­trado en nuestro articulo [4]. Así concluimos que todos l os operadores de tipo (5 a) entran en una sola clase de equivalen­cia relacionada con el grupo total G (r) N cuyo representante más sencillo es B , (o B 2 , a nuestra elección).

3. Clasificación de los operadores de simetría hacia tercer orden

Buscamos un operador de tercer orden:

de la condición de conmutación [ Á , B J = o . Después de cálculos sencillos obtenemos las funciones: a , b, e, d, f, lo que nos perm ite presentar dicho operador como una combina­ ción cubica de tres operadores de base (5 b):

donde las constantes p , P , "( , Ó , E , , µ, V , 11 , 8 son cualesquiera. Ahora con la transformación ( 3) del subgrupo G y las form ulas (7) empezamos la clasificación de los operadores de simetría de tercer orden (8):

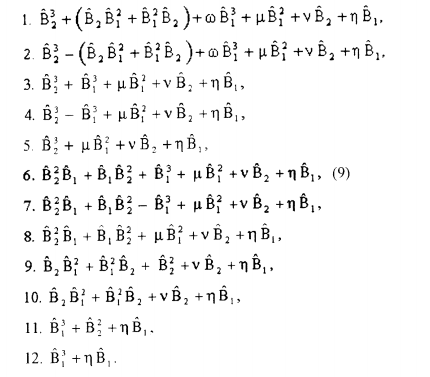
Aquí w , µ .v , 11 son las constantes (los parámetros) cua­ lesqu iera. Si en la formula (8) todos los coeficientes delante de los operadores de tercer orden se anulan, pasamos a la clasificación de los operadores de segundo orden:

Ahora podemos establecer equivalencia de algunas clases de los operadores de simetría usando las transformaciones del subgrupo N (4) y las formulas (6). Así encontramos que las clases 9 y 10 de los operadores del tercer orden de las formu­las (9) son equivalentes a la clase 8 para los valores específicos del parámetro µ . De la misma manera, las clases 11 y 12 de las formulas (9) entran como casos particulares en la clase 5. Estos resultados permiten formular el teorema siguiente.

Teorema l. Sea el operador Á de la ecuación ( l). Todos los operadores lineales diferenciales hacia tercer orden que conmutan con A. entran en una de l 4 clases de equivalencia siguientes:

los opera dnres del tercer orden: clases de 1 a 8 de la formula (9),
los operadores del segundo orden. clases de la 5 de la fórmula (10).
los operadores del primer orden: una sola clase de lafórmula (11).

Notamos que todas las clases de los operadores del tercer orden son parametrizadas por tres o cuatro parámetros cua­ lesquiera, lo que sign ifica que en realidad tenemos no ocho clases, sino ocho agrupaciones de clases de equivalencia de los operadores _de simetría. Contrariamente a este hecho, los representantes más sencillos de seis clases de equivalencia de los operadores del primer y del segundo orden no tienen nin­ gún parámetro. En nuestro articulo [3] encontramos todas las 5 clases de los operadores del segundo orden, pero los representantes men­ cionados contienen algunos parámetros.

Aquí comprobamos que estos resultados se pueden simplificar: véase la formula ( 1O). La solución particular de la ecuación de Schrodinger (1) en la forma de una onda sin dispersión del articulo [5] también entra en nuestra clasificación mientras que sea parametrizada: la integral de movimiento correspondiente entra en la clase de equivalencia 4 de la formula ( 1O). Además en nuestro trabajo antecedente [3] hacemos la dis­tinción entre las clases B y B, de los operadores del pri­mer orden.

El estudio actual muestra que éste es inútil visto que estos operadores son equivalentes con respecto al subgru­po N. La clasificación de los operadores de simetría hacia el segundo orden mencionada en el libro [2] no corresponde a la nuestra porque está hecha en función de la posibilidad de separar las variables en la ecuación ( 1 ). Observamos que el autor menciona también seis clases de los operadores del se­gundo y del primer orden.

Concluimos que la clasificación definida por el Teorema 1 contiene todos los casos conocidos en la literatura de los ope­radores de simetría y es más compacta que ciertas clasificacio­nes antecedentes. Todos los resultados relacionados con l os operadores del tercer orden son nuevos. También podría ser interesante estudiar los operadores de simetría que no están en conmutación con el operador Á de la ecuación ( 1 ), sino solo en el caso cuando el conmutador sea proporcional a Á .

Bibliografía

1. C. Boyer ( 1974). "The maximal kincmat i calinvariance group for an arbitrary potential". Helv. PhysAua , v. 47. 589 - 605.

2. W. Miller, Jr., Symmetry and Separarion o{ Variahles, Addison­ Wesley Publishing Company. London, 1977.

3. N. Sukhomlin, T. Shovgurova ( 1982). Simmetry and exact solu­tions of the Schrodinger ecuación I, Prsprint. VINITI, El istaStat University.

4. N. Sukhomlin, M. Arias (2003), Electromagnetic fields classifica­ tion in the no relativistmechanics (in publication).

5. Americashki

6. V. Shapovalov, N. Sukhomli n ( 1 974). "'Separation of variables in the Schrodinger equation", Sov. Phys. Rev., 1975, v.