i INTRODUCCION
Es comun escuchar a las autoridades monetarias (Banco Central) anunciar que tomaran medidas con la finalidad de restringir (expandir) la cantidad de dinero en circulación y de esta manera lograr que aumenten (disminuyan) las tasas de interes del mercado. El objetivo de dichas autoridades en un momenta determinado del tiempo puede ser, p. ej., evitar la devaluación de la moneda o facilitar el acceso al credito por parte del sector privado mediante una reducción en el costo del mismo.
Detrás de este tipo de acciones se encuentra uno de los conceptos mas controversiales en macroeconomia: el ejecta liquidez (Cagan y Gandolfi, 1968; Friedman, 1968; Cagan, 1972). Numerosos estudios han analizado empiricamente dicho efecto a nivel intemacional (por ejemplo Gibson, 1968; Mishkin, 1983; Melvin, 1983; Reichenstein, 1987.; Cochrane, 1989; Bemanke y Blinder, 1992; Gali, 1992; Leeper y Gordon, 1992; Pagan y Robertson, 1995; Strongin, 1995; Hamilton, 1997; Bernanke y Mihov, 1998). La evidencia presentada por los citados (y otros) estudios es mixta, encontrando algunos resultados a favor y otros en contra de la existencia del efecto liquidez.
Concretamente, el efecto liquidez estipula que, en el corto plazo, una expansion de la cantidad de dinero en circulacion generara una reduccion en las tasas reales de interes, y viceversa. Dicho efecto, no obstante, puede ser dominado por el efecto inflacion. Es decir, las tasas de interes podrian aumentar, en vez de disminuir, como consecuencia de una expansion de la cantidad de dinero en circulacion. El efecto inflacion es generalmente relacionado con expansiones anticipadas de la cantidad de dinero. Por el contrario, las expansiones no anticipadas son relacionadas al efecto liquidez. Este ultimo mecanismo se encuentra fuertemente relacionado con la literatura propuesta por la Nueva Economias Clásica (por ejemplo Lucas, 1990).
La determinacion de la existencia de un efecto liquidez para el caso de una economia en particular es, obviamente, una cuestion empirica. El principal objetivo del presente trabajo es investigar el efecto liquidez para el caso de la Republica Dominicana. Los resultados de dicho analisis podrian ser de interes para las autoridades monetarias y los estudiosos de la economia dominicana en general.
El resto de la investigacion esta organizado de la siguiente manera. La seccion 2 describe las tecnicas econometricas a ser implementadas en el analisis. En la seccion 3 son llevadas a cabo las estimaciones empiricas. La seccion 4 concluye la investigacion.
ii. METODOLOGIA ECONOMETRICA
Enfoque tradicional
El enfoque tradicional para el amilisis econometrico del efecto liquidez ha considerado una ecuación de rezagos distribuidos del tipo

siendo r el nivel de la tasa de interes nominal, el crecimiento del agregado monetario y L el operador de rezagos, definido de manera tal que Las estimaciones empiricas de la ecuación (1) son, en la actualidad, generalmente llevadas a cabo mediante tecnicas modemas de series de tiempo, como lo son, por ejemplo, los minimos cuadrados ordinarios dinamicos (DOLS, por sus siglas en ingles, Stock y Watson, 1993), los vectores autoregresivos (VARs) y los multiples analisis derivados de los mismos.
La estimación de (1) debe arrojar una correlación negativa en el corto y positiva en el largo plazo, entre el crecimiento del dinero y la tasa de interes. Ademas, la mencionada correlación debe ser de mayor magnitud para el caso de la relación entre la variaciones no-anticipadas en el crecimiento del dinero y la tasa de interes, y menor entre las variaciones anticipadas en el crecimiento del dinero y la tasa de interes, lo cual reflejara el impacto del efecto inflación.
Vectores autoregresivos (VARs)
Para obtener información acerca del comportamiento de las variables bajo amilisis como un conjunto es conveniente tratar cada una de estas simetricamente. Esta metodol ogia es implementada con regularidad en analisis de sistemas macroeconómicos, dadas las criticas que existen sobre las estimaciones basadas en ecuaciones simultaneas (Sims, 1980).
En el caso de dos variables (x e y), la aplicación de la tecnica de vectores autoregresivos (VARs) implicaria el permitir que la trayectoria de y1 das de la serie x 1 sea afectada por realizaciones actuales y pasay viceversa.
Esto puede ser escrito como
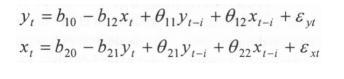
Se asume que en las ecuaciones (3 a) y (3 b) tanto x1 como y1 son estaciones, y que son residuos ruido blanco, no correlacionados, con desviaciones estandares σy y σx respectivamente.
Modelo ADL
El modelo general de rezagos autoregresivos distribuidos (ADL, por sus iniciales en ingles) ha sido extensamente usado, tanto directamente como en sus diversos casos especiales. El modelo, por ejemplo, ADL (1,1), puede ser definido como
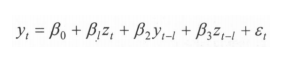

iii. ESTIMACIONES
Datos Dadas la obvias ventajas metodológicas de las mismas, el presente estudio se enfocara en la aplicación de la tecnica de VARs y el modelo ADL. Los datos a ser utilizados son el M1 nominal, en millones de pesos dominicanos, y la tasa de interes (promedio de los bancos comerciales) nominal (activa) de 1-90 dias, expresada en puntos porcentuales anuales. La fuente de ambas series es el Banco Central de la Republica Dominicana y las mismas abarcan el periodo comprendido entre Agosto del 1991 ( 1991.08) y marzo del 1999 (1999.03). las variables seran denotadas por m y R, respectivamente, indicando la letra minuscula, en el caso del M1, el logaritmo de la misma.
Nótese que la tasa de interes considerada es una de corto plazo, ya que, como habia sido mencionado anteriormente, en el largo plazo el efecto liquidez muy probablemente estara dominado por el efecto inflación. Ademas, el lector debe percatarse de que el estudio no realizara distinción entre las variaciones anticipadas y no anticipadas en la cantidad de dinero.
Dada la muy conocida importancia de la estacionariedad o no de las series bajo analisis para la validez de las estimaciones econometricas basadas en minimo cuadrados ordinarios (MCOs), el orden de integración de las mismas debe ser determinado. Para tales fines sera apicada fa prue ba de Dickey-FuHer Aumentad a (ADF por sus siglas en ingles, Dickey y Fuller, 1981).
La prueba ADF esta basada en una regresión de la forma

donde εt es un error estocastivo, y a y t son un termino constante y una tendencia temporal, respectivamente. La prueba ADF corresponde al valor de la raz6n t del termino ɸ en la ecuación (5), siendo la hip6tesis nula el que y t es una serie no estacionaria, la cual es rechazada cuando ɸ es significativamente negativa.
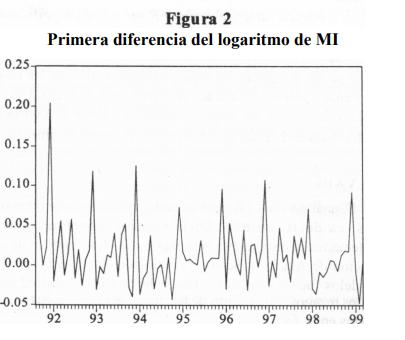
Los resultados de aplicar la prueba ADF (ecuación (5)), sin incluir tendencia temporal, a Δm y R son (-5 .66), significativo al 99%, y (-2.91 ), significativo al 95%, respectivamente. Es decir, las variables Δm y R son integradas de orden cero (1(0)), por lo tanto puede procederse al analisis econometrico de las mismas sin temor a obtener resultados de regresiones espureas. Las Figuras 1 y 2 pueden ser inspeccionadas con fines de constatar la estacionariedad de las variables Δm y R, respectivamente.
VARs
El analisis de VARs fue iniciado con rezagos de doce periodos, es decir, un año. Dichos rezagos fueron reduci dos sistematicamente a nueve, seis, tres y uno. Los criterios de información de Akaike y Schawarz estimados para cada uno de los modelos fueron empleados para seleccionar la longitud optima de los rezagos. Los valores de las mencionadas pruebas son mostrados en la Tabla 1.


La regla utilizada en la selección de modelos es elegir aquellos con los criterios de información mas pequefios. Para el presente caso, el modelo con rezago de un periodo es el mas adecuado de acuerdo a los criterios empleados. Los resultados de la estimación del VAR con un rezago pueden ser escritos como
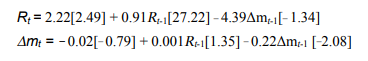
donde los valores entre corchetes son estadísticos t. El coeficiente de mayor interés es el que acompaña a la variable Δm en la ecuación (6a). El mismo posee el signo esperado, negativo, y una magnitud razonable. Por cada 1% que aumente la cantidad de MI en la economía dominicana la tasa de interés activa de 1 - 90 días cargada por los bancos comerciales disminuirá en 4.39 puntos porcentuales, aproximadamente.
Sin embargo, nótese que dicha variable es significativa solo marginalmente. Ademas, las pruebas de diagnóstico aplicadas al sistema compuesto por (6a) y (6b) señalan la existencia de autocorrelación (AR 1-6 F(24,148) = 1.9618[0.0080]) y de no normalidad (NORM X 2 (2) = 43.811 [0.0000]) en los residuos.
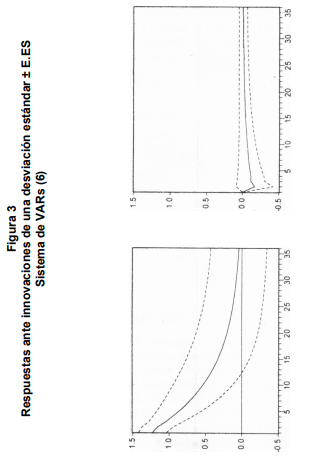
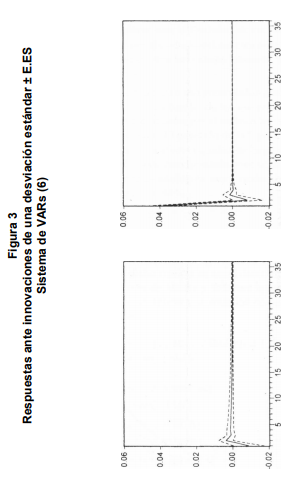
No obstante las fallas marginales del sistema analizado anteriormente, se procedió a la estimación de las funciones de respuesta impulsiva del mismo, con la finalidad de estimar el impacto sobre las innovaciones (residuos) del sistema de un choque de una desviación estandar sobre los valores presentes y futuros de las variables endógenas.
Los resultados de dicho analisis son presentados graficamente a traves de la Figura 3. Las bandas de los errores de la respuestas impulsivas fueron estimadas por el metodo Monte Carlo a partir de 10,000 repeticiones. El panel (b) de la Figura 3 refleja claramente la existencia de un efecto liquidez de larga vida. Dicho efecto, sin embargo, es de muy pequeña magnitud en relación al nivel de la de interes analizada, cuya media durante el periodo bajo estudio fue de 26.46%.
ADL (1,1)
Como evidencia adicional a la presentada por la estimación del sistema (6) la investigación analiza un modelo ADL (1, 1). El orden de los rezagos de dicho modelo es aquel determinado por los criterios de información de Akaike y Sxhwarz aplicados anteriormente. El resultado de aplicar una ecuación como (4) a la relación que nos ocupa es

El modelo (7) cumple satisfactoriamente con las pruebas de correlación serial (AR), de heterocedasticidad condicional autoregresiva (ARCH), de heterocedasticidad (HET) y de normalidad de Ramsey (RESET). Ademas, el mismo explica, aproximadamente, un 90% de las variaciones en R. El ajuste del modelo puede ser inspeccionado a traves de la Figura 4.
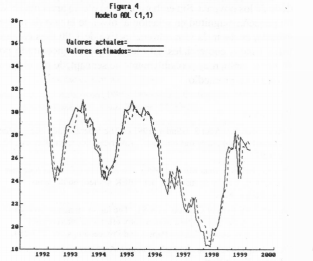
Todos los coeficientes de la ecuación (7) son significativos al menos al 95% de probabilidad, con la excepción del coeficiente de Amt-1 que lo es al 90%. La tasa de interes sigue practicamente un proceso autoregresivo de orden uno AR( l ). La presencia de un efecto liquidez es captada a traves del coeficiente de la variación contemporanea y rezagada de la cantidad de dinero. Con un 95% de probabilidad puede esperarse que, en promedio, un aumento de 1% en la cantidad de M1 reduzca contemporaneamente la tasa de interes nominal de 1-90 dias en 7.09 puntos porcentuales.
CONCLUSIÓN
La respuesta a la pregunta planteada por el titulo del presente articulo es positiva, aunque de caracter conservador. Las estimaciones de vectores autoregresivos (VARs) y de un modelo autoregresivo de rezagos distribuidos (ADL) señalan la existencia de un efecto liquidez en la economia dominicana durante la decada de los noventa. Sin embargo, dicho efecto aparenta ser de muy pequeña magnitud en relación al nivel de la tasa de interes analizada, es decir, la tasa nominal activa de 1-90 dias cargada por los bancos comerciales. El efecto liquidez encontrado podria, por lo tanto, muy probablemente no ser captado por el agente económico promedio.
REFERENCIAS
Bernanke, Ben S. y Alan S. Blinder (1992). “The federal funds rate and the channels of monetary transmission”, American Economic Review, 82, 901-921.
Bernanke, Beb S. y Ilian Mihov (1998). The liquidity effect and long-run neutrality, trabajo de discusión del NBEK número 6608, junio, Cambridge, MA.
Cagan, Philip y Artrhur Gandolfi (1968). “The lag in monetary policy as implied by the time pattem of monetary effects on interest rates”, American Economic Review Papers and Proceeedings, 59, 277-284.
Cagan, Philip (1972). The channels of monetary effects on interest rates, NBER, Nueva York.
Cochrane, John (1989). “The retum of the liquidity effect: a study of the short-run relation between money growth and interest rates”, Journal of Business and Economic Statistics, 7, 75-83.
Dickey, D.A. y W.A. Fuller (1981). “The likelihood ratio statisrics for autoregressive time series with a unit root”, Econometrica, 49, 105772.
Friedman, Milton (1968). “The role of monetary policy”, American Economic Review, 58, 1-17.
Gali, Jordi (1992). “How well does the IS-LM model fit postwar US data?” Quarterly Journal of Economics, 107, 709-738.
Gibson, W.E. (1968). “The lag in the effect of monetary policy on income and interest rates”, Quarterly Journal of Economics, 85, 288-300.
Hamilton, Jameds D. (1997). “Measuring the liquidity effects”, American Economic Review, 87, 80-97.
Lucas, Robert E., Jr. (1990). “Liquidity and interest rates”, Journal of Economic Theory, 50, 237-264.
Leeper, Eric M. y David B. Gordon (1992). “In search of the liquidity effects”, Journal of Monetary Economics, 29, 341-369.
Melvin, M. (1983). “The vanishing liquidity effect of money on interest: analysis and implications for policy”, Economic Enquiry, 21, 188-202.
Mishkin, F. (1983). A rational expectations approach to macroeconomics: testing policy ineffectiveness and efficient market models, imprenta de la Universidad de Chicago, Chicago.
Pagan, A. y J. Robertson (1995). “Resolving the liquidity effect”, Federal Reserve Bank of St. Louis Review, 77, 33-54.
Reichenstein, W. (1987). “The impact of money on short-term interest rates”, Economic Enquiry, 25, 67-82.
Stock, James y Mark Watson (1993). “A simple estimator of cointegrating vectors in higher order integrated systems”, Econometrica, 61, 783820.
Sims, C. (1980). “Macroeconomics and reality”, Econometrica, 48, 1-48. Strongin, S. (1995). “The identification of monetary policy disturbances: explaining the liquidity puzzle”, Journal of Monetary Economics, 35, 463-497.
Strongin, S. (1995). “The identification of monetary policy disturbances explaining the liquidity puzzle”, Journal of Monetary Economics, 35, 463-497.
