1. Descripción de la data
En la siguiente figura se presenta la evolución de las tres tasas de interés en el período comprendido entre enero de 2008 y septiembre de 2014, para un total de 81 observaciones mensuales. La media de la tasa de interés overnight en ese período fue de 6.04%, con un valor máximo de 9.5% y un mínimo de 4.0%. La media de la tasa de interés activa en ese período fue de 15.59%, con un valor máximo de 25.17% y un mínimo de 10.74%. El promedio de la tasa de interés pasiva fue de 7.02%, con un valor máximo de 13.49% y un mínimo de 3.79%.
Figura N.° 1 - Tasa de interés
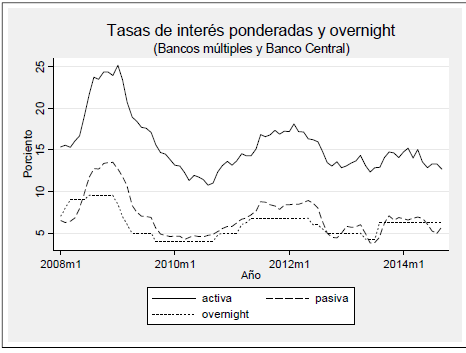
El cambio absoluto de las tasas de interés activa y pasiva se distribuye normalmente. Un análisis de normalidad basado en la asimetría y la curtosis no permite rechazar la hipótesis nula de normalidad de esas variables. En contraste, el cambio absoluto de la tasa de interés de política monetaria no se distribuye normalmente. La prueba basada en asimetría y curtosis permite rechazar la hipótesis nula de normalidad para el caso de la tasa de interés overnight. Ese resultado se debe una concentración de valores alrededor de cero por encima de lo esperado en una distribución normal.
Tabla N.° 1 Skewness/Kurtosis for Normality

Los histogramas de los cambios de las tasas de interés sugieren claramente que las tasas de interés activa y pasiva se distribuyen normalmente, con un valor centrado en cero. La variabilidad de las tasas de interés activa es superior a la del resto de las tasas de interés. Los cambios absolutos de la tasa de interés activa exhiben una desviación estándar 1.3 veces superior a la tasa de interés pasiva y dos veces mayor que la registrada por la tasa de interés de política monetaria. Ese resultado se expresa también en un mayor rango de oscilación de la tasa de interés activa, con relación al resto de las tasas de interés.
Figura N.° 2
Tasa de interés activa
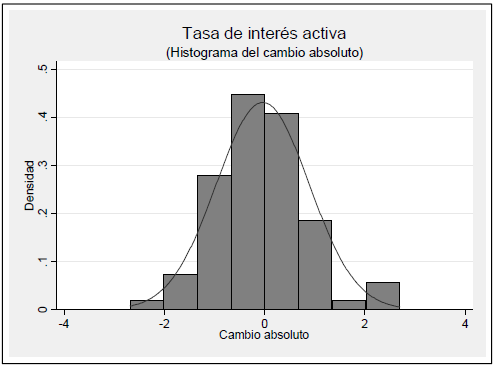
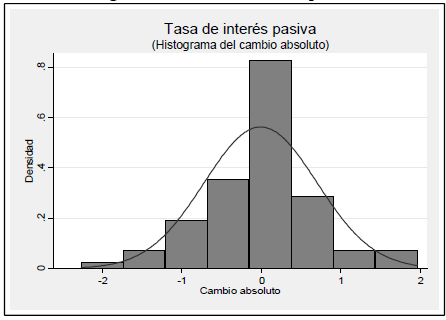
Figura N.° 3 - Tasa de interés pasiva
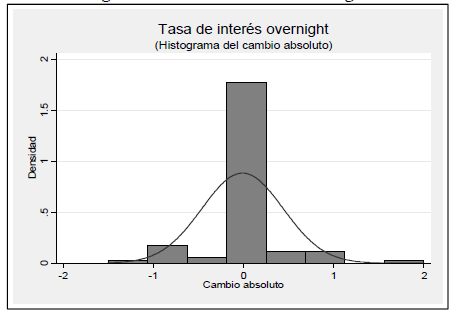
El histograma de la tasa de interés overnight muestra una curtosis muy superior a la de una distribución normal. Esa excesiva concentración alrededor de cero es lo que permite rechazar la hipótesis nula de normalidad en los cambios de la tasa de interés overnight.
Figura N.° 4 - Tasa de interés overnight
2. Análisis de raíces unitarias y cointegración
Para evitar que el análisis econométrico entre las tasas de interés sea el resultado de relaciones espúreas es imprescindible determinar primero si son estacionarias. Para esto se evaluó la existencia de raíces unitarias aplicando a cada una de las variables la prueba Dickey-Fuller aumentada.1 La hipótesis nula es que la variable contiene una raíz unitaria. La hipótesis alternativa es que la variable fue generada por un proceso estacionario en media y varianza.
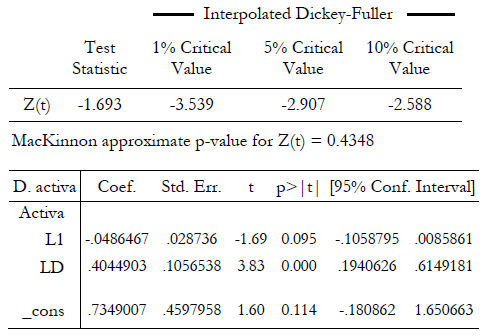
Prueba de raíz unitaria para la tasa de interés activa. Los resultados arrojan un valor del estadístico t que no permite rechazar la hipótesis nula. Por tanto, la serie tasa de interés activa no es estacionaria.
Tabla N.° 2
Augmented Dickey-Fuller test for unit root Number of obs = 79
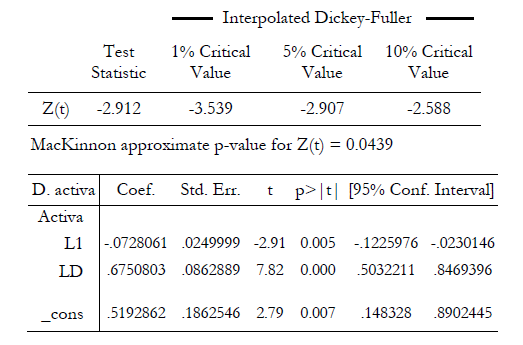
Prueba de la raíz unitaria para la tasa de interés pasiva. Para un valor crítico de 1% de significancia no se puede rechazar la hipótesis nula. En consecuencia, la tasa de interés pasiva tampoco es una variable estacionaria.
Tabla N.° 3
Augmented Dickey-Fuller test for unit root Number of obs = 79
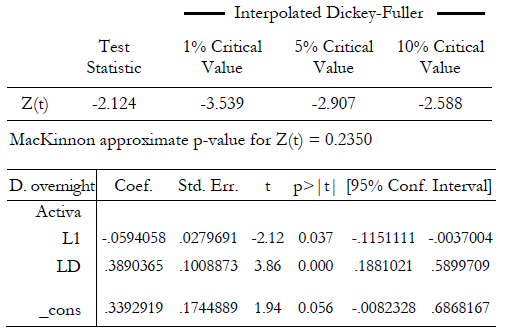
Prueba de la raíz unitaria para la tasa de interés overnight. El estadístico t arroja un valor que no permite rechazar la hipótesis nula de raíz unitaria. La serie no es estacionaria.
Tabla N.° 4
Augmented Dickey-Fuller test for unit root Number of obs = 79
Las tres tasas de interés .–en niveles–. resultaron ser no estacionarias. La única forma de que exista una relación no espúrea entre variables no estacionarias es si existe una relación de largo plazo entre ellas. La prueba de cointegración tiene dos etapas.2 La primera realiza una regresión de la variable tasa de interés activa con relación a la tasa de interés de política monetaria y se obtienen los residuos de ese modelo. La segunda realiza una prueba de raíz unitaria de los residuos. Si los residuos son estacionarios se dice que existe cointegración entre las variables. Las pruebas de cointegración permiten determinar si existe esa relación de largo plazo entre la tasa de interés activa y la overnight, y entre la tasa de interés pasiva y la overnight. A continuación se presentan los resultados.
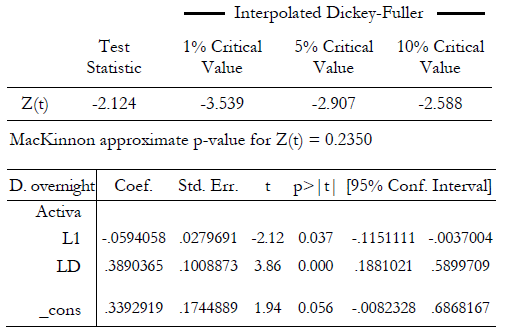
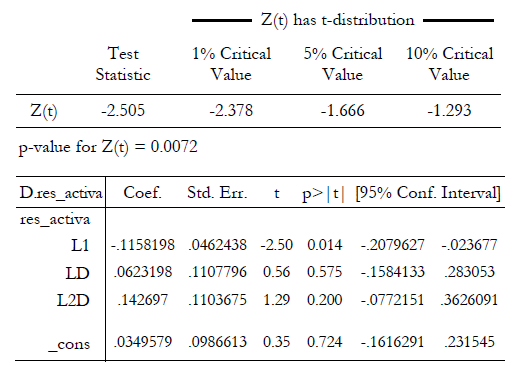
Prueba de cointegración entre la tasa de interés activa y overnight. Se realizó una prueba de raíz unitaria de los residuos incluyendo un término de deriva y el resultado del estadístico t arrojó que se puede rechazar la hipótesis nula de raíz unitaria. En consecuencia, se puede afirmar que los residuos son estacionarios y existe cointegración entre la tasa de interés activa y la tasa overnight. Esto permitiría estimar un modelo econométrico con ambas variables expresadas en niveles.
Tabla N.° 5
Augmented Dickey-Fuller test for unit root Number of obs = 78
----------- Z(t) has t-distribution ------
Prueba de cointegración entre tasa de interés pasiva y overnight. El valor del estadístico t permite rechazar la hipótesis nula de raíz unitaria. Por lo tanto, los residuos son estacionarios y la tasa de interés pasiva y la overnight cointegran. Se puede estimar un modelo econométrico con ambas variables expresadas en niveles.
Tabla N.° 6
Augmented Dickey-Fuller test for unit root Number of obs = 79
3. Modelos econométricos para las tasas de interés activa y pasiva
El modelo econométrico especificado para la tasa de interés activa permitirá obtener la reacción de corto y largo plazo a los movimientos de la tasa de interés overnight. Se estimará un modelo de rezagos geométricos distribuidos, utilizando la transformación de Koyck.3
El efecto de corto plazo, en el primer período, de un aumento de un punto porcentual de la tasa de interés overnight es medido por B. En los períodos siguientes existe una influencia de la tasa overnight a través de la tasa de interés activa retrasada un período. Transcurridos T períodos el efecto del cambio de una unidad de la tasa overnight sobre la tasa activa es igual a (1 - pT) B / (1- p). La respuesta de largo plazo, que representa el cambio en la variable dependiente asociada con el cambio de una unidad de la variable explicativa que se mantiene por siempre (i.e., cuando (T --> ∞), es del tiempo T para el cual la fracción del ajuste completado es igual a la mitad. En este caso, el retraso medio es igual a:
El modelo econométrico estimado para la tasa de interés activa arrojó como resultado la siguiente ecuación. El valor del estadístico t permite señalar que la tasa de interés overnight ejerce una influencia estadísticamente significativa sobre la tasa de interés activa. Asimismo, se observa que el parámetro que acompaña a la variable dependiente rezagada es estadísticamente diferente de cero. El modelo explica el 95% de la desviación de los movimientos de la variable dependiente.
Tabla N.° 7

Dado que la transformación de Koyck puede producir correlación serial, lo cual hace que los parámetros estimados no sean eficientes, se aplicó la prueba h de Durbin para determinar la correlación serial. El resultado indica que no existe correlación serial.
Tabla N.° 8
Durbin's alternative test for autocorrelation

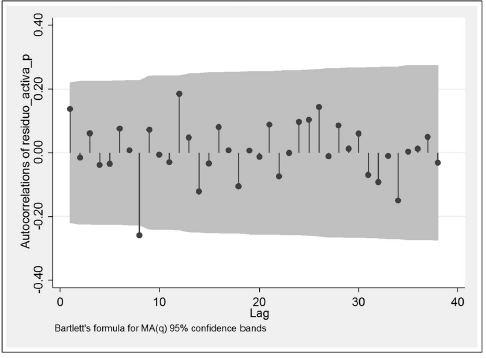
También se realizó un correlograma a los residuos del modelo de regresión de la tasa de interés activa para determinar si existe correlación serial. El resultado del correlograma revela que los residuos no tienen información sistemática adicional. Esto confirma nuevamente que los parámetros estimados son eficientes.
Figura N.° 5
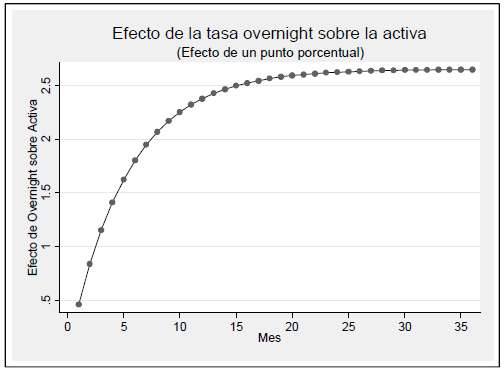
Los parámetros permiten señalar que el multiplicador de corto plazo (T = 1) es igual a ß = 0.457. Esto significa que por cada punto porcentual que se incremente la tasa de interés overnight, la tasa de interés activa se incrementará en ese mismo mes en casi medio punto porcentual. Con el transcurrir del tiempo el efecto del aumento de un punto de la tasa de interés overnight produce un incremento de . Esto significa un aumento de 2.66 puntos porcentuales en la tasa de interés activa. La evolución del efecto (multiplicador) a lo largo del tiempo se presenta en la siguiente figura. Nótese que en los primeros doce meses se llega a un valor cercano al ajuste de largo plazo. La mitad del ajuste ocurre en los primeros 3.7 meses (i.e., )
Figura N.° 6
Efecto de la tasa overnight sobre la activa
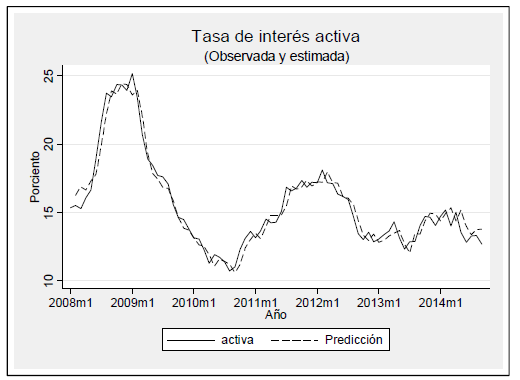
El modelo econométrico permite realizar predicciones de la tasa de interés activa, dado el movimiento de la tasa overnight. La bondad de ajuste se muestra en la siguiente figura. Cabe resaltar que desde mayo de 2014 la tasa de interés activa se encuentra por debajo del valor pronosticado. Esto significa que otros factores, no recogidos por la tasa de interés de política monetaria .–que se ha mantenido constante desde finales de agosto de 2013–., explican el descenso de las tasas de interés. En otras palabras, si fuera por la tasa de interés overnight la tasa de interés activa observada fuese .–en promedio–.0.9 puntos porcentuales más alta.
Figura N.° 7
Tasa de interés activa (observada y estimada)
El modelo econométrico especificado para la tasa de interés pasiva es el siguiente.
El modelo econométrico estimado para la tasa de interés pasiva fue corregido mediante el uso del método Cochrane-Orcutt debido a la existencia de correlación serial. Los coeficientes de las variables explicativas son estadísticamente diferentes de cero. El modelo explica el 86% de los movimientos de la tasa de interés pasiva.
Tabla N.° 9

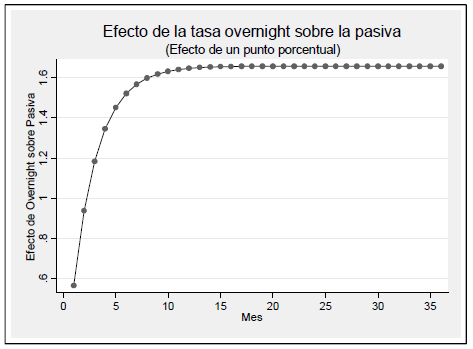
Los parámetros estimados permiten señalar que el multiplicador de corto plazo (T = 1) es igual a ß = 0.564. Esto significa que por cada punto porcentual que se incremente la tasa de interés overnight, la tasa de interés pasiva se incrementará en ese mismo mes en 0.56 de punto porcentual. Con el transcurrir del tiempo el efecto del aumento de un punto de la tasa de interés overnight produce un incremento de . Esto significa un aumento de 1.65 puntos porcentuales en la tasa de interés pasiva. La evolución del efecto (multiplicador) a lo largo del tiempo se presenta en la siguiente figura. Nótese que en los primeros nueve meses se llega a un valor cercano al ajuste de largo plazo. La mitad del ajuste ocurre en los primeros 1.66 meses (i.e, )
Figura N.° 8
Efecto de la tasa overnight sobre la pasiva
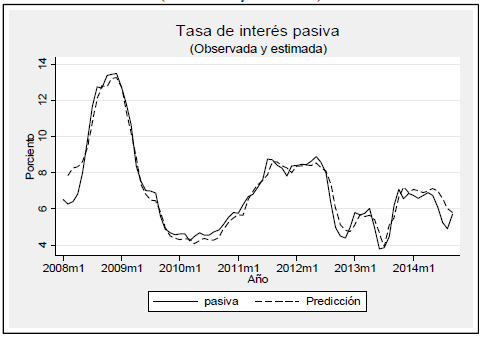
El modelo econométrico permite realizar predicciones de la tasa de interés pasiva, dado el movimiento de la tasa de interés overnight. La bondad de ajuste se muestra en la siguiente figura. Se observa que desde noviembre de 2013 la tasa de interés pasiva proyectada supera –en promedio–. en 0.5 puntos porcentuales a la tasa de interés pasiva observada. A septiembre de 2014 la diferencia se redujo a menos de 0.09 puntos porcentuales.
Figura N.° 9
Tasa de interés pasiva(observada y estimada)
La comparación de la reacción de ambas tasas de interés permite concluir que en el corto plazo la tasa de interés pasiva reacciona a los movimientos de la tasa overnight en mayor magnitud que la tasa de interés activa. Además, la tasa de interés pasiva llega a su nivel de equilibrio de largo plazo más rápido. No obstante, cabe resaltar que en el largo plazo la magnitud del cambio –en términos absolutos– de la tasa de interés activa es mayor que el cambio de la tasa de interés pasiva.
4. Conclusiones
Los dos modelos de tasas de interés estimados pueden ser estimados para predecir, con varios meses de antelación, el impacto que tendrían las decisiones del Banco Central respecto a la tasa de interés de política monetaria (overnight.) Esto permitiría a los intermediarios financieros, a los inversionistas y a los tesoreros adoptar medidas que permitan maximizar la rentabilidad de sus posiciones en instrumentos de renta fija y, simultáneamente, minimizar el riesgo de mercado que producen los movimientos bruscos e inesperados de las tasas de interés.
Como complemento a la presente investigación, en un próximo artículo se analizarán los determinantes de la tasa de interés de política monetaria. Ese objetivo implica especificar y estimar la función de reacción del Banco Central a los movimientos de la tasa de inflación, del PIB real, del tipo de cambio y a las condiciones externas.
Notas
- Véase Hamilton (1994).
- Véase en Engle y Granger (1991) una colección extraordinaria de estudios sobre el uso de las técnicas de cointegración para analizar las relaciones económicas de largo plazo. Véase también Johansen (1996) y Hansen y Johansen (1998).
- Véase Koyck (1954). También puede encontrarse una buena presentación de los modelos de rezagos distribuidos y la transformación de Koyck en Pindyck y Rubinfeld (2001).
5. Referencias bibliográficas
Engle, R. F. & Granger, C. W. (Eds.). (1991). Long-Run Economic Relationships. Advanced Texts in Econometrics. Oxford: Oxford University Press.
Franses, P. H. & Van Oest, R. (2004). On the econometrics of the Koyck model. Econometric. Rotterdam: Erasmus University Rotterdam.
Hansen, P. & Johansen, S. (1998). Workbook on Cointegration. Advanced Texts in Econometrics. Oxford: Oxford University Press.
Hamilton, J. D. (1994). Time series analysis. New Jersey: Princeton University Press.
Johansen, S. (1996). Likelihood-based inference in cointegrated vector autoregressive models: Advanced texts in econometrics. (2da. Ed.). Oxford: Oxford University Press.
Koyck, L. M. (1954). Distributed lags and investment analysis. Amsterdam: North-Holland.
Pindyck, R. & Rubinfeld, D. L. (1999). Econometría: Modelos y pronósticos. (4ta. Ed.). México: McGraw-Hill.
Datos de filiación
Jaime Aristy Escuder. Licenciado en Economía Summa Cum Laude INTEC (1985); doctorado en Economía por la Universidad de Barcelona (1989); magíster en Matemáticas Puras (PUCMM, 1994); master of Science en Financial Mathematics Universidad de Chicago (2003). Desde 1989 ha sido profesor de Economía Matemática y de Econometría en la PUCMM, INTEC y en la Universidad Católica de Santo Domingo, tanto a nivel de maestría como a nivel de licenciatura. Ha escrito y colaborado en 10 libros publicados en la República Dominicana o por casas editoriales extranjeras (Fondo de Cultura Económica y McGraw-Hill). Autor de ensayos que han sido presentados en las Universidades de MIT, Stanford, Harvard y Londres. Es Egresado Destacado (2011) del Instituto Tecnológico de Santo Domingo.
Email: jaimearisty@gmail.com
