Ciencia y Educación, Vol. 9, No. 1, enero-abril, 2025 • ISSN (impreso): 2613-8794 • ISSN (en línea): 2613-8808
GEOTIC: PROPUESTAS INNOVADORAS PARA LA ENSEÑANZA DE GEOMETRÍA EN EL NIVEL MEDIO
GEOTIC: innovative proposals for the teaching of geometry at the secondary level
DOI: https://doi.org/10.22206/cyed.2025.v9i1.3394
Florencia Belén González1
ORCID: https://orcid.org/0009-0006-4090-0216
Lucía Primo Brochiero2
ORCID: https://orcid.org/0009-0003-1622-3460
Natalia Fátima Sgreccia3
Recibido: 29/11/2024 • Aceptado: 19/03/2025
Cómo citar: González, F. B., Primo, L. & Sgreccia, N. F. (2025). GEOTIC: propuestas innovadoras para la enseñanza de geometría en el nivel medio. Ciencia y Educación, 9(1), 51-60. https://doi.org/10.22206/cyed.2025.v9i1.3394
Resumen
Este estudio analiza la integración de la Modelización Matemática (MM) en la enseñanza de la geometría mediada por el software matemático GeoGebra. Se indaga cómo estudiantes avanzadas del Profesorado en Matemática de la Universidad Nacional de Rosario (Argentina) comprenden la MM en la resolución de problemas geométricos. Con un enfoque cualitativo y un diseño exploratorio basado en microclases, con dos participantes, abordando contenidos geométricos mediante MM y software. Los hallazgos muestran que las estudiantes no lograron completar un ciclo de modelización desde la perspectiva cognitiva, lo que sugiere la necesidad de un mayor trabajo en la construcción del significado de la MM en la enseñanza. Este estudio aporta una reflexión sobre la formación docente y el rol del software en la comprensión geométrica, destacando la importancia de guiar el proceso de modelización en futuros profesores, para que esto pueda tener un gran impacto en sus futuros alumnos.
Palabras clave: formación de docentes, modelo matemático, geometría, software didáctico.
Abstract
This study analyzes the integration of Mathematical Modeling (MM) in the teaching of geometry mediated by the mathematical software GeoGebra. It investigates how advanced students of the Mathematics Teaching career of the National University of Rosario (Argentina) understand MM in solving geometric problems. With a qualitative approach and an exploratory design based on microclasses, with two participants, addressing geometric content through MM and software. The findings show that the students failed to complete a modeling cycle from the cognitive perspective, suggesting the need for further work in the construction of the meaning of MM in teaching. This study provides a reflection on teacher training and the role of software in geometric understanding, highlighting the importance of guiding the modeling process in future teachers, so that this can have a great impact on their future students.
Keywords: teacher training, mathematical model, geometry, teaching software.
Introducción
Este trabajo surgió como una propuesta innovadora que quiere mejorar y construir el conocimiento en la formación de docentes en la carrera Profesorado en Matemática radicado en la Facultad de Ciencias Exactas, Ingeniería y Agrimensura de la Universidad Nacional de Rosario (FCEIA-UNR, Argentina). Su foco es conocer el abordaje de la geometría, a partir de la Modelización Matemática (MM), en aula de nivel secundario (estudiantes de 13 a 18 años), con mediación de algún software matemático.
En el Diseño Curricular Jurisdiccional de la provincia de Santa Fe (donde se ubica la ciudad de Rosario) se expresa: “el hacer matemática es un trabajo de modelización cuyo motor consiste en la resolución de problemas” (Ministerio de Educación de la provincia de Santa Fe, 2014). El documento ministerial considera que la modelización y la resolución de problemas están entrelazados. La MM se caracteriza por brindar una perspectiva integral de la actividad matemática, con diversos aspectos como problemas, técnicas, representaciones, demostraciones, sin que necesariamente alguno predomine sobre los demás. Reconoce a la resolución de problemas como uno de los caminos para la construcción de conocimiento, diferenciándose de la concepción tradicional en la que los problemas se presentan como una instancia de aplicación de lo previamente enseñado. El abordaje de esta práctica de enseñanza facilita establecer una relación entre el mundo real y la matemática. Para estudiantes de nivel secundario esto permite fomentar una motivación en el proceso de aprendizaje y ayudar a los estudiantes a construir conceptos matemáticos (Ministerio de Educación de la provincia de Santa Fe, 2014).
A lo largo de los meses dedicados a esta investigación, se ha hecho una selección de diversos artículos sobre MM, TIC y/o formación docente. Un enfoque con el que se acuerda en este trabajo es la diferenciación entre MM y resolución de problemas. Esta última se caracteriza por resolver preguntas matemáticas específicas focalizadas en la solución de situaciones particulares de contextos matemáticos y extramatemáticos que pueden ser abordados con métodos, técnicas y algoritmos; mientras que la MM implica la creación de modelos matemáticos para entender y resolver problemas del mundo real. Puede definirse como la interacción entre el mundo real y el mundo matemático, “una relación con una realidad física o conceptual compleja para la cual se plantea un modelo que la representa y que describe aquellos aspectos sustanciales y relaciones funcionales” (Chavarría Vázquez y Gamboa Araya, 2024, p.3).
El trabajo con modelización en el aula se suele desarrollar en pequeños grupos de estudiantes, a quienes se les plantea una situación-problema a matematizar. Esta situación-problema requiere ciertas características (Arcos et al., 2018), tales como: es abierta y compleja; su resolución no se limita a una respuesta o procedimiento específico; los estudiantes tienen que buscar los datos relevantes; es realista y auténtica; comprende elementos del mundo real; es solucionable a través de un ciclo de modelización con el desarrollo de todas sus fases (Figura 1).
Figura 1
Ciclo de modelización desde una perspectiva cognitiva
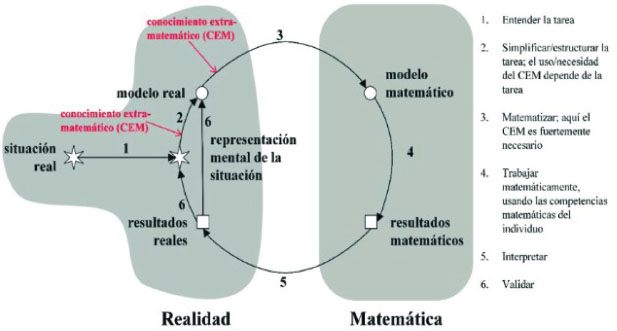
Fuente: Adaptación de Arcos et al. (2018, p.15).
En cuanto a la MM en la formación de futuros profesores, resulta relevante trabajarla como una estrategia didáctica y no como una simple resolución de problemas (Chavarría Vásquez y Gamboa Araya, 2024, p.23). Incluso reconociéndose la necesidad de incorporar el abordaje de la MM como parte del plan de estudios desde lo teórico y conceptual (Villarreal y Mina, 2020). Esto permite conocer sobre diferentes concepciones, dificultades, competencias, procesos y ciclos asociados a ella; además, promover la concientización de su uso en el aula para contextualizar la matemática a la vida real.
En efecto, se identifican cuatro Procedimientos de Resolución (PR) definidos como submódulos del ciclo de modelización desde una perspectiva cognitiva (Ledezma et al., 2024). Estas categorías de los PR en una situación de MM en estudiantes avanzados en el Profesorado permiten poder establecer una orientación sobre las etapas identificadas en las producciones sobre el ciclo de modelización.
• PR1: no evidencian una comprensión completa del enunciado del problema y/o solo aportan una descripción de cómo podría ser resuelto.
• PR2: desarrollan las fases modelo real/modelo matemático y matematizan el problema para darle respuesta.
• PR3: abordan las fases modelo real / modelo matemático / resultados matemáticos. Consideran suficiente obtener resultados matemáticos a partir del modelo matemático para resolver los problemas, sin necesidad de interpretarlos como resultados reales ni validarlos.
• PR4: desarrollan el ciclo de modelización completo (pp.64-65).
En la actualidad, en las aulas, se percibe una predominancia de la mera exposición de los contenidos geométricos sin una vinculación con situaciones cotidianas. La enseñanza de la geometría ocupa un lugar central en el desarrollo del pensamiento espacial y la comprensión de las formas y estructuras que nos rodean. Esta área de la matemática no solo permite analizar y describir figuras, sino que también brinda las herramientas para resolver problemas prácticos en áreas como arquitectura, ingeniería y física (Sgreccia, 2012).
La MM permite desarrollar el pensamiento geométrico (Andonegui Zabala citando a Guzmán, 2006) a través del abordaje de modelos. Dado que brinda una capacidad de traducir problemas del mundo real a un lenguaje matemático concreto, resulta esencial en la resolución de desafíos prácticos y en la toma de decisiones informadas (Bassanezi, 1994). En efecto, en la formación de futuros docentes el trabajo de MM posibilita los procesos de construcción de conocimientos geométricos, la reflexión de los procesos involucrados y la validación que a su vez emerjan conocimientos didácticos, matemáticos y tecnológicos (Cruz et al., 2020).
La integración de software matemático en la MM puede potenciar la experiencia educativa. Más aún, la incorporación de las Tecnologías de Información y Comunicación (TIC) trae aparejado modificaciones que tienen que ver con el trabajo matemático de los alumnos (Borsani et al., 2016), tanto en las actividades que se pueden abordar como en la forma de hacerlo, lo que promueve un ambiente experimental que cambia la naturaleza del aprendizaje. También, con el trabajo de los profesores que llevan al aula este tipo de actividades, se consideran nuevos conocimientos y espacios de decisión, acorde al término TPCK (Technological Pedagogical Content Knowledge) (Mishra y Koehler, 2006). Ello comprende no solo el conocimiento del contenido de la disciplina, tecnológico y pedagógico, sino también las complejas relaciones entre estos componentes. De esta manera, permite “construir escenarios educativos superadores” (Brunini et al., 2018, p.149) con un reconocimiento al potencial de las tecnologías al integrarse en los procesos de enseñanza y aprendizaje.
Respecto a software educativos, el GeoGebra pone en juego un universo de objetos y relaciones que configura, a su vez, un modelo recortado de la geometría euclídea (Borsani et al., 2016). Este tipo de herramienta brinda visualización y manipulación dinámica de una amplia gama de conceptos matemáticos en un marco funcional, y su utilización es intuitiva y de fácil acceso para estudiantes de nivel secundario. También se utilizan relaciones geométricas e implica una serie de elecciones a través de las cuales se produce necesariamente un recorte en vinculación con una situación geométrica modelizada. Por último, es un software de uso gratuito, lo que lo hace una herramienta accesible para llevar al aula.
En la educación matemática, la integración de MM en la enseñanza de la geometría a través del uso de software podría representar un aporte significativo. Esta aproximación no solo permite a los estudiantes la construcción del sentido de los conceptos geométricos a través de la modelización de manera interactiva, sino que también fomenta el desarrollo de habilidades analíticas y la resolución de problemas mediada por el uso de las TIC; es decir, asumiendo una visión amalgamada tanto en términos pedagógicos como epistemológicos de la matemática (Cámara y Mancipar, 2007). También permite movilizar conocimientos previos, tomar decisiones y por lo tanto tomar una postura crítica a diversas situaciones en el proceso de la construcción de conocimientos (Cruz et al., 2020).
A partir de estas consideraciones, el trabajo tiene como objetivo principal analizar cómo la integración de la MM en el abordaje de la geometría mediada por software matemático puede favorecer el aprendizaje de los estudiantes en el nivel medio. En específico, con foco en estudiar cómo consideran los futuros docentes universitarios en Matemática de la UNR a la MM en la comprensión de conceptos geométricos y la resolución de problemas, y explorar cómo argumentan sus decisiones al respecto, siendo esto también una contribución en el marco de su formación inicial como futuros docentes.
Metodología
El presente estudio tiene enfoque cualitativo ya que se orienta en comprender los fenómenos y explorarlos desde la perspectiva de los participantes en un ambiente natural y en relación con su contexto (Hernández-Sampieri y Mendoza, 2018). Puntualmente, quienes participan en este trabajo son dos estudiantes avanzadas de la carrera Profesorado en Matemática en cuestión. Ambas se encuentran cursando las últimas materias; en particular, el seminario Proyectos Innovadores en Educación Matemática, con el que culminan su formación inicial. Precisamente, fueron elegidas por tal condición de estudiantes próximas a graduarse e insertarse al ámbito laboral.
El tipo de trabajo que se realizó fue un diseño exploratorio basado en microclases (Pujol-Cols et al., 2023), con la premisa de contribuir a mejorar la práctica docente de Profesores en Matemática sobre la integración de la MM en la enseñanza de la geometría mediada por software matemático. Las microclases se diseñaron para analizar con ellas propuestas que abordan contenidos geométricos integrados con MM y software. Se implementaron en el aula habitual de clase, que es un laboratorio de informática de la institución formadora (FCEIA), con una duración 120 minutos la primera y 90 la segunda. En la primera de ellas, además, se presentó un breve resumen de la teoría en la que se basa este trabajo, dando a conocer los conceptos de MM y TIC, con preguntas a pensar entre todos los participantes antes del desarrollo de las consignas. Entre ellas, “¿Es lo mismo resolver problemas en matemática que modelizar? La enseñanza de la matemática mediada por tecnologías, ¿utopía o realidad?”. Estas preguntas quedaron abiertas en la presentación que se mostró en la clase y luego se intercambió con las estudiantes en cuanto a tales disparadores y lo que ellas pensaban sobre su formación respecto a este tema. Luego se presentó la consigna de actividad, con la premisa de estudiar el conocimiento y argumentación de las futuras profesoras en Matemática sobre el trabajo de la MM, con problemas relacionados al área de la geometría, mediados por el uso de GeoGebra.
Plantear la siguiente situación problemática, utilizando de manera conveniente el software GeoGebra para su exploración y explicitar el contenido trabajado, junto con el curso donde podría implementarse.
Una vez planteada la actividad, responder: ¿Cómo incorporaron el uso de software GeoGebra en la resolución de la situación problemática? ¿Qué aporte cree que ofrece este tipo de actividades en su formación docente?
Las propuestas de las situaciones problemáticas invitaban a la formulación de modelos matemáticos como herramientas para las conjeturas de propiedades. Para ello, se realizó un sorteo para la distribución de estas a cada una de las estudiantes.
Actividad 1: La escalera del pintor
Jorge es pintor de casas y también hace distintas reparaciones de fachadas de casas. En su trabajo necesita una escalera, pero no tiene dinero para comprar una de extensión, entonces decide hacer tres escaleras de manera que pueda trabajar. Necesita saber de qué medidas van a ser. También necesita saber qué escalera llevar de acuerdo al trabajo que le salga. ¿Qué medidas de escalera necesita Jorge para pintar una casa de dos pisos?
(Extraído de Téllez, 2021)
Actividad 2: El parque de bomberos
El ayuntamiento de tres pueblos cercanos quiere construir un parque de bomberos que cubra las necesidades de los tres. ¿Dónde lo situarías para que, en el caso de incendio en alguno de los pueblos, el camión de bomberos tardase lo menos posible en llegar?
(Extraído de Gámez y Ramírez, 2015)
Para la recolección de datos del primer encuentro, se utilizaron notas de observación registradas por las docentes durante las microclases, enfocándose en el accionar de las estudiantes, sus comentarios, dudas y estrategias de resolución. También se solicitaron informes escritos, en los cuales las estudiantes debían explicar su proceso de resolución y reflexionar sobre la integración de software en la actividad.
En el segundo encuentro, se realizaron entrevistas individuales a las participantes con el objetivo de profundizar en su experiencia, su percepción sobre la MM y el uso de software GeoGebra en la enseñanza de la geometría.
Para el análisis de los datos, se utilizaron las PR como marco conceptual, permitiendo categorizar las estrategias utilizadas por las estudiantes y su nivel de comprensión del ciclo de modelización. Se analizó su capacidad para formular y argumentar soluciones matemáticas, la relación entre lo producido y el uso de GeoGebra, así como las dificultades que enfrentaron en la aplicación del ciclo de modelización.
Resultados
Las alumnas involucradas (desde ahora llamadas R y S) han trabajado con GeoGebra antes, en su formación docente y han escuchado el concepto MM. En el primer encuentro, luego de presentar los conceptos, se puede observar que comienzan con el planteo de las situaciones utilizando lápiz y papel. La alumna R pregunta si puede investigar, por ejemplo, cuánto mide una casa de dos pisos aproximadamente, para utilizar ese dato en el problema. Se plantea, de parte de las docentes, analizar esto como un caso base y luego pensarlo de forma más general. La alumna S visualiza que los tres pueblos están conectados mediante un triángulo. Se le recomienda comenzar a explorar los otros casos, a analizar cuáles podrían ser otras posibilidades.
En el segundo día, las estudiantes lograron un avance respecto al primer encuentro. S siguió trabajando en su idea de los tres pueblos conectados en forma de triángulo y las docentes vuelven a enfatizar: “¿Qué otras posibilidades en la disposición de los pueblos hay?”. Esto se debe a que previamente se ha pensado en los casos en que los pueblos se encuentren formando triángulos que no tengan todos ángulos agudos y también ubicados en línea recta (equidistantes o no). Las profesoras repreguntan: “¿Qué pasaría si dos pueblos al menos no estuviesen conectados por una ruta?”. Pudo manifestar que el problema permite trabajar con “manipulación de elementos geométricos” como mediatriz, puntos, segmentos, y que con él se pueden aplicar conceptos de distancia y conjeturar acerca de los puntos notables de un triángulo. Destaca como una fortaleza que se puede ver a la actividad desde distintos enfoques según el año de dictado.
Sin embargo, en la entrega de su informe, la alumna solo se quedó con el análisis del primer caso y los demás hablados en los encuentros no fueron explorados. De esta manera, la estudiante determina como una posible resolución:
Sean A, B y C los pueblos. Supongamos que no están alineados dos a dos. Cada pueblo representa un vértice de un triángulo acutángulo. Lo que buscamos es minimizar la distancia entre cada pueblo y el punto donde se ubique el parque de bomberos.
Entonces procedemos a buscar la mediatriz de cada lado del triángulo, de manera que donde se intersecan las tres mediatrices sea el punto donde se ubicará el parque de bomberos. Es decir, el circuncentro, punto donde equidista de los tres vértices del mismo.
Con respecto a la pregunta “¿En qué curso podría desarrollarse?”, S plantea que podría darse en un primer o segundo año, de acuerdo con los contenidos abordados. Cita pasajes del Diseño Curricular (Ministerio de Educación de la provincia de Santa Fe, 2014) para dar una idea de cómo están organizados los temas que nombró.
En cuanto al software, la futura docente S plantea que los alumnos podrán explorar y manipular herramientas de geometría para plantear y resolver la situación problemática, de acuerdo con los contenidos matemáticos dados; o sea, considera que la actividad tiene resolución solo a través de las herramientas que provee GeoGebra. Además, remarca que este tipo de tareas permite al docente incorporar tecnología en la enseñanza y promover la participación de los estudiantes, con la visualización de los conceptos de forma dinámica. Considera que el software sirve de apoyo en los procesos de enseñanza y de aprendizaje, permite a los estudiantes interactuar con objetos, buscar posibles soluciones a partir de su manipulación, considerar los conocimientos adquiridos y aplicarlos a la resolución de problemas.
Por su parte, en el segundo encuentro, R comienza a desprenderse de la idea de las medidas numéricas. En efecto, plantea a las docentes que ha pensado en dos aplicaciones del problema: dar Teorema de Pitágoras para un 1er año del ciclo básico, o dar Trigonometría en un 3er año, con uno de los ángulos con medida incluida desde el inicio en la actividad. Además, se puede observar en ella una confusión: “En esta actividad, ¿me tengo que poner en el rol del estudiante o de la docente?”.
Cabe advertir que en la microclase, su rol asumido es el de docente, mientras que las profesoras a cargo tratan de ponerse en el rol del estudiante que tiene que resolver este tipo de tarea. También, de acuerdo con lo mencionado, se proponen algunas sugerencias con relación a su planteamiento; como, por ejemplo, llamar c1 a la vereda (primer cateto), c2 al frente de la casa (segundo cateto) y h a la escalera del pintor. Aquí R propone que con GeoGebra puede ir variando estas longitudes y utilizar diversas herramientas como puntos y segmentos. A partir de esto, las docentes interpelan a ambas estudiantes: “¿Qué pasaría si los estudiantes desconocen el Teorema de Pitágoras?”, la respuesta queda vacante.
Al entregar el informe, la construcción de R es la siguiente (Figura 2).
Figura 2
Imagen del informe de la alumna R
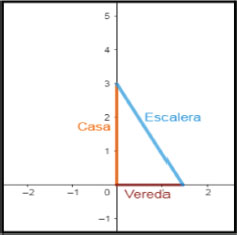
Fuente: Captura de resolución de la estudiante.
Si bien se pidió una posible resolución, la futura docente acompañó la imagen con la respuesta siguiente:
Mediante esta propuesta, lo que se intenta es introducir la relación pitagórica que establece que donde c1, c2 (longitud de los catetos) hacen referencia a la longitud de la casa y la vereda, indistintamente, y h (longitud de la hipotenusa) hace referencia a la longitud de la escalera.
Considera que el uso del GeoGebra puede ser valioso, ya que los estudiantes son invitados a explorar distintas situaciones, mediante la variación de cualesquiera de las tres longitudes y luego observar, deducir y conjeturar lo que sucede con ellas; pero no especifica cómo. También propone que la tarea puede ser una actividad a utilizar en el momento de aplicación del tema o como actividad final. En cuanto al aporte a su formación docente, lo piensa como una herramienta para su futuro, para implementar con diversos temas, y que resulta muy útil para conocer cómo piensan y razonan los estudiantes, saber qué herramientas utilizan para resolver este tipo de situaciones y cuáles son las dificultades, si es que las hay, a la hora de enfrentarse con problemas de esta índole.
Conclusiones y discusiones
El presente estudio permitió explorar la integración de la MM en la enseñanza de la geometría mediada por software en la formación docente. A lo largo del análisis, se identificaron varios puntos clave que este proceso involucra (Figura 1).
Las estudiantes consideran lo que dice el Diseño Curricular Jurisdiccional (Ministerio de Educación de la provincia de Santa Fe, 2014) para ubicar a la actividad en uno de los años de escolaridad, realizando una conexión con los problemas seleccionados de geometría con los mencionados en el documento ministerial. Además, enfatizan en la importancia y el valor del software didáctico, en este caso GeoGebra, como una herramienta de innovación destacada en las aulas tanto para los docentes como para los estudiantes. Ello encuentra eco con lo señalado por Borsani et al. (2016, p.58) en cuanto a que “este tipo de propuestas promueve un ambiente experimental que probablemente cambie la naturaleza del aprendizaje”.
El ciclo de modelización desde una perspectiva cognitiva (Figura 1), en términos de los procedimientos de resolución de las estudiantes, se asocian exclusivamente a PR1 (Ledezma et al., 2024); es decir, limitándose a describir posibles estrategias sin desarrollar completamente un modelo matemático. Es en estos términos que se presentó cierta desconexión entre la teoría y la práctica en la formación docente, en procesos como por ejemplo de validación (Cruz et al., 2020).
A pesar de que las estudiantes explicitan haber trabajado previamente con el GeoGebra y haber estudiado conceptos relacionados a la MM, encontraron dificultades para aplicarlo en la resolución de problemas en un sentido pleno (Chavarría Vásquez y Gamboa Araya, 2024). Por ejemplo, necesitaron datos numéricos para llegar a una solución o no utilizaron el software para formular conjeturas de los problemas propuestos.
A partir de estos hallazgos, se sugiere para una implementación efectiva de la MM, un acompañamiento intencional y sistemático durante la formación inicial, como también sugieren Villarreal y Mina (2020), desde los primeros años de la carrera. Ello se puede realizar mediante talleres específicos o brindar un tratamiento con un enfoque trasversal en las asignaturas que son relacionadas a la formación de docentes.
La integración de MM en la enseñanza de la geometría mediada por software requiere una articulación entre el conocimiento tecnológico, pedagógico y del contenido (TPCK). En este estudio, se observó que las futuras docentes poseen un conocimiento tecnológico básico sobre GeoGebra, pero su uso fue limitado en la resolución de problemas. En cuanto al conocimiento pedagógico, enfrentaron dificultades para planificar las actividades de modelización y proponer una guía de secuencias para llevarla a cabo en las aulas del nivel secundario.
Finalmente, en relación con el conocimiento del contenido, aunque las futuras profesoras lograron establecer algunas conexiones con el Diseño Curricular Jurisdiccional (Ministerio de Educación de la provincia de Santa Fe, 2014), la construcción de modelos matemáticos resultó escasa, ya que las estudiantes trabajan frecuentemente con problemas más estructurados. Es por esto que la implementación de este tipo de propuestas por parte de las estudiantes es un aspecto para seguir trabajando, en términos pedagógico-epistemológicos (Cámara y Mancipar, 2007).
A modo de cierre, se destaca que esta experiencia aporta una primera aproximación a la integración de la MM en la enseñanza de la geometría mediada por software dentro de la formación docente. Lo reportado evidencia la necesidad de fortalecer la articulación entre contenido, pedagogía y tecnología, ofreciendo un tratamiento integral a los futuros docentes a desarrollarse para implementar estas estrategias de enseñanza en el aula. En futuras investigaciones, se espera replicar esta experiencia con una mayor cantidad de participantes y en distintos contextos educativos, con el fin de profundizar en el impacto de la MM y su potencial para la enseñanza de la geometría en la educación secundaria.
Referencias
Andonegui Zabala, M. (2006). Geometría: conceptos y construcciones elementales. Serie desarrollo del pensamiento matemático. UNESCO. https://scioteca.caf.com/handle/123456789/531
Arcos, J. H., Borromeo-Ferri, R., y Mena-Lorca, J. J. F. (2018). El conocimiento de la modelación matemática desde la reflexión en la formación inicial de profesores de matemática. Enseñanza de Ciencias, 36(1), 99-115. https://doi.org/10.5565/rev/ensciencias.2277
Bassanezi, R. (1994). Modelling as a teaching-learning strategy. For the Learning of Mathematics, 14(2), 31-35. https://www.jstor.org/stable/40248113
Borsani, V., Cedrón, M., Cicala, R. A., Di Rico, E., Duarte, B., y Sessa, C. (2016). Modelización de relaciones entre magnitudes geométricas en un entorno enriquecido con TICs: actividades para la escuela secundaria, diseñadas en un grupo colaborativo. Yupana, (10), 56-69. https://doi.org/10.14409/yu.v0i10.7697
Brunini, G., Chirino, F., y Donato, V. (2018). GeoGebra: un software paradigmático. En N. Sgreccia (Coord.). Procesos de acompañamiento en la formación inicial y continua de profesores en Matemática (pp.119-151). FarenHouse. https://dialnet.unirioja.es/servlet/libro?codigo=720072
Cámara, V., y Marcipar, S. (2007). La construcción del sentido de conceptos matemáticos desde la modelación. Ciencias Económicas, 2(7), 31-44. https://doi.org/10.14409/ce.v2i7.1110
Chavarría-Vásquez, J., y Gamboa Araya, R. G. (2024). Significados y perspectivas en modelización matemática de un cuerpo docente formador en Enseñanza de la Matemática de una universidad pública costarricense. Actualidades Investigativas en Educación, 24(1), 1-27. https://doi.org/10.15517/aie.v24i1.55560
Cruz, M. F., Esteley, C., y Scaglia, S. (2020). Una experiencia de formación para futuros profesores: producir matemática en un contexto de modelización matemática vinculada con fenómenos geométricos. Educación Matemática, 32(1), 193-220. https://doi.org/10.24844/EM3201.09
Cruz, M. F., Mántica, A., y Gallo, M. (2020). Experiencia de modelización matemática llevada a cabo con futuros profesores. Números, 103, 13-28. https://dialnet.unirioja.es/servlet/articulo?codigo=7287086
Gámez, C., y Ramírez, R. (2015). Problemas de modelización para todos los públicos. Aires, 5(2), 1-11. https://hdl.handle.net/10481/64631
Hernández-Sampieri, R., y Mendoza, C. (2018). Metodología de la investigación. Las rutas cuantitativa, cualitativa y mixta. McGraw Hill Education. https://doi.org/10.22201/fesc.20072236e.2019.10.18.6
Ledezma, C., Morales-Maure, L., y Font, V. (2024). Experiencia educativa en modelización para docentes de matemática en Panamá. Alteridad, 19(1), 58-70. https://doi.org/10.17163/alt.v19n1.2024.05
Ministerio de Educación de la provincia de Santa Fe. (2014). Diseño Curricular. Educación Secundaria Orientada. Ministerio de Educación de la provincia de Santa Fe. https://www.santafe.gov.ar/index.php/educacion/content/download/218364/1135170/file/Anexo%20III%20Resol%202630-14.pdf
Mishra, P., y Koehler, M. J. (2006). Conocimiento del contenido tecnológico pedagógico: Un marco para el conocimiento docente. Teachers College Record, 108(6), 1017-1054. https://doi.org/10.1111/j.1467-9620.2006.00684.x
Pujol-Cols, T. H., García, M. B., y Cutrera, G. (2023). Desarrollo profesional en el contexto de la formación docente inicial. Un estudio de caso centrado en la microclase como dispositivo formativo. Diálogo entre as Ciências, 12(1), 340-361. https://doi.org/10.22481/rbba.v12i01.11673
Sgreccia, N. (2012). La geometría del espacio en el Profesorado en Matemática: la generación de puentes entre la formación disciplinar y didáctica [Tesis de Doctorado]. Universidad Nacional de Rosario.
Téllez, L. K. A. (2021). Teorema de Pitágoras a través de la modelación con software de geometría dinámica [Tesis de Maestría]. Instituto Politécnico Nacional.
Villarreal, M., y Mina, M. (2020). Actividades experimentales con tecnologías en escenarios de modelización matemática. Bolema, 34(67), 786-824. https://doi.org/10.1590/1980-4415v34n67a21
_______________________________
1 Universidad Nacional de Rosario, Argentina. Email: fgonza@fceia.unr.edu.ar
2 Universidad Nacional de Rosario, Argentina. Email: lprimo@fceia.unr.edu.ar
3 Universidad Nacional de Rosario, Argentina. Email: sgreccia@fceia.unr.edu.ar
