Estrategias pedagógicas para el aprendizaje de las operaciones matemáticas básicas sin calculadora

1. Introducción

Las matemáticas, a través de los años, han sido percibidas por los estudiantes como una asignatura difícil y exacta, debido a sus contenidos abstractos y a las metodologías de enseñanza aprendizaje repetitivas (Marin y Mejía, 2016), donde se reproducen y memorizan ejercicios para luego plasmarlos en un examen, generando rechazo en los alumnos por la carencia de significado en su vida cotidiana (López, 2014). Cambiar estas perspectivas y lograr un aprendizaje significativo en matemáticas es un reto para todos los docentes (López, 2014; Etchepare, et. al., 2017).

Las evaluaciones nacionales e internacionales hacen evidente el bajo rendimiento en matemáticas en los estudiantes dominicanos. En el Programa Internacional de Evaluación de los Alumnos (PISA por sus siglas en inglés) (OCDE, 2016), la República Dominicana quedó en la última posición en matemáticas, obteniendo 139 puntos de 436. Asimismo, el Tercer Estudio Regional Comparativo y Explicativo (TERCE) mostró el bajo nivel de dominio numérico de los estudiantes dominicanos de tercer y sexto grado, donde solo el 26 % y 21 %, respectivamente, respondieron correctamente. Estas pruebas contenían situaciones cotidianas donde se hace necesaria la resolución de problemas, y por ende, el uso de operaciones matemáticas. Por tanto, es necesario que el estudiantado aprenda a trabajar con ellas, conozcan su sentido y puedan utilizarlas de manera apropiada en sus distintos contextos.

Este estudio presenta una experiencia de investigación-acción en la que se diseñaron y ejecutaron secuencias didácticas enfocadas en la resolución de problemas de la vida cotidiana y el empleo de recursos lúdicos, para que los estudiantes de secundaria desarrollen la capacidad de efectuar las operaciones matemáticas básicas sin la necesidad de utilizar la calculadora. La metodología implementada se fundamentó en las estrategias de aprendizaje que plantea el Diseño Curricular Dominicano del Nivel Secundario (MINERD, 2016), como son el aprendizaje significativo y el aprendizaje por descubrimiento.

2. Marco teórico

Estrategias de enseñanza aprendizaje

A través de los años se han dado muchas definiciones del concepto de estrategias de enseñanza y aprendizaje. Una de las más completas es la dada por Guaráte y Hernández (2018), quienes precisan dichas estrategias como:

El conjunto de acciones y procedimientos, mediante el empleo de métodos, técnicas, medios y recursos que el docente emplea para planificar, aplicar y evaluar de forma intencional, con el propósito de lograr eficazmente el proceso educativo en una situación de enseñanza-aprendizaje específica, según sea el modelo pedagógico y/o andragógico por: contenidos, objetivos y/o competencias para las cuales las elabora y desarrolla (p.1).

En este sentido, el currículo dominicano también las define como:

…secuencias de actividades y procesos, organizados y planificados sistemáticamente, para apoyar la construcción de conocimientos y el desarrollo de competencias. Posibilitan que el estudiantado enfrente distintas situaciones, aplique sus conocimientos, habilidades y actitudes en diversos contextos. Las estrategias son intervenciones pedagógicas realizadas en el ámbito escolar que potencian y mejoran los procesos y resultados del aprendizaje (MINERD, 2016, p. 42).

Dentro de las estrategias de aprendizaje que plantea nuestro currículum, podemos encontrar el aprendizaje significativo, el aprendizaje por descubrimiento y la resolución de problemas.

En la teoría del aprendizaje significativo, las implicaciones didácticas requieren que el maestro relacione los conocimientos previos que ya tiene el alumno, con la clase que vaya a impartir, para así partir de un terreno estable al terreno desconocido. David Ausubel (citado por Moreira, 2012, p. 3) sostiene que “se da un aprendizaje significativo cuando el estudiante asocia una información nueva con la que posee, dándole un significado en su propia realidad”.

Por otro lado, al utilizar la estrategia del aprendizaje por descubrimiento, el docente en lugar de explicar cómo resolver la situación planteada, proporciona los recursos, materiales y herramientas apropiadas para que los educandos realicen observaciones, elaboren conjeturas y comprueben si las mismas son correctas (Bruner, 2011). Esta estrategia permite que el estudiante se apropie de su aprendizaje, además, el elemento sorpresa proporciona una motivación adicional, ya que le mantiene activo, desarrollando conjeturas, descartándolas o validándola, y al final se siente satisfecho y disfruta lo aprendido, pues descubre contenidos o teorías que, aunque sean existentes, para él son nuevas.

Asimismo, la resolución de problemas es una estrategia donde los estudiantes pueden dedicarse de manera independiente y autónoma a la búsqueda de ideas y tácticas para alcanzar una solución adecuada al problema planteado (Mora, 2003). George Pólya (1945), plantea que para resolver un problema matemático se deben seguir los siguientes pasos “1. comprender el problema, 2. concebir un plan, 3. ejecución del plan y 4. examinar la solución obtenida” (p. 17). Es muy importante recordar estos pasos, ya que para la resolución de un problema primero se lleve a un lenguaje matemático, el cual no necesariamente responde a la pregunta del problema. En muchos casos, hay que interpretar lo que nos dice la respuesta para traducirla de nuevo a un lenguaje cotidiano. 

El juego como recurso didáctico

El juego es una estrategia metodológica que se puede implementar en todos los niveles educativos, sin embargo, persisten muchas resistencias a su uso debido a muchas causas, entre ellas: el apego a las prácticas convencionales, la falta de conocimiento o formación de los docentes para ejecutarlos. También, requieren más trabajo y preparación (Higueras, 2019). Hoy en día, son muchos los autores que lo validan como una herramienta fundamental en nuestras aulas.

Muchas veces, las matemáticas resultan pesadas y tediosas para los estudiantes por falta de motivación y monotonía, sin embargo, para Blasco (2017):

Aprender matemáticas no tiene que ser aburrido. El componente lúdico debe estar presente en los aprendizajes. Los niños y las niñas a través de los juegos pueden experimentar gran cantidad de relaciones matemáticas de forma espontánea que posteriormente, podrán asimilar e interiorizar. (p. 4)

En otro orden, Chacón (2008) propone las siguientes características al momento de utilizar un juego didáctico en la clase de matemáticas: 1. Debe servir para que los alumnos profundicen y amplíen los significados de las nociones matemáticas. 2. Ser útiles, provocando procesos de reflexión sobre las nociones que se quieren desarrollar. 3. Ser adecuados a los objetivos que se han trazado para su trabajo. 4. Deben permitir que los alumnos puedan discutir las ideas y los descubrimientos que van surgiendo mientras juegan. Estas recomendaciones son necesarias puesto que se refieren a juegos didácticos, los cuales tienen que estar bien orientados a fines educativos, con reglas que regulen su uso y que guíen a un aprendizaje del contenido curricular, no solo al ocio y a competir.

Uso de la calculadora en la enseñanza-aprendizaje de las matemáticas

En la actualidad existen varios debates y creencias relacionados con el uso de la calculadora en las aulas y su impacto en los aprendizajes del estudiantado. Entre los mismos grupos de estudiantes hay pensamientos muy distintos al respecto, algunos defienden su uso considerando que son indispensables y que no pueden vivir sin ellas, además de que la necesitarán en los estudios post secundaria, otros, creen que son inútiles, provocan daños cognitivos y entumecen el cerebro (Campos, 2013).

En este sentido, Peralta et al. (1991) sugieren que el uso de dicha herramienta ayuda en la adolescencia al paso del pensamiento concreto al pensamiento abstracto; esto, en base al estudio de los hemisferios cerebrales, porque la calculadora ofrece un enlace entre la sensación táctil y la representación simbólica, integrando los procesamientos de ambos hemisferios. Además, promueven que se introduzca en el salto del nivel primario al nivel secundario.

Por otro lado, las calculadoras no resuelven problemas por sí solas, para resolverlos es necesario usar el razonamiento y conocer los algoritmos propios de cada operación (Samaniego y Rodrigo, 2013). Además, puesto que no muestran la procedencia de los resultados, usándolas se pierden oportunidades para fortalecer razonamientos y destrezas matemáticas (López et. al., 2017). Los estudiantes primero deben desarrollar el cálculo mental, la comprensión, pensar y razonar con independencia de cualquier máquina. Posterior a esto, se puede incluir el uso de la calculadora para comprobar los resultados de problemas más complejos, (Samaniego, 2013; Granados, 2019) para ahorrar tiempo y esfuerzo (Minnaard y Del Puerto, 2002).

El error como oportunidad de aprendizaje en matemáticas

“La mente del alumno no es una página en blanco: el alumno tiene un saber anterior, y estos conocimientos anteriores pueden ayudar al nuevo conocimiento, pero a veces son un obstáculo en la formación del mismo” (Del Puerto, Minnaard y Seminara, 2006, p. 3); porque si ese conocimiento se basa en una información equivocada puede generar errores en la incorporación del nuevo aprendizaje. En matemáticas, “El tipo de error más común se debe al aprendizaje deficiente de conocimientos previos y al escaso manejo de destrezas matemáticas elementales” (Cadenas, 2007, p. 70). Los errores que cometen los estudiantes según Lozzada y Ruiz (2011), “no deben ser ignorados, más bien se pueden utilizar para profundizar en su pensamiento matemático, logrando así atender sus problemáticas y, además, intentar que los mismos se constituyan en un importante elemento motivador” (p. 30). En este sentido, Gonzaga (2019) plantea que el error debe verse como una oportunidad de mejora que permita a los involucrados implementar nuevas estrategias para obtener una mejor comprensión.

Por último, es imprescindible realizar una buena elección de las estrategias, que servirán de instrumento para los procesos de enseñanza y aprendizaje y conocer los algoritmos que están ocultos en las calculadoras. Hay que ser conscientes de que existen más estrategias para enseñar y aprender matemáticas, pues cada día se descubren nuevas formas en las que los estudiantes aprenden, sin embargo, las seleccionadas en este marco teórico responden a necesidades actuales de la educación y al enfoque constructivista, sirviendo para desarrollar competencias y generar interés en los estudiantes.

3. Metodología

El objetivo general de este estudio es presentar una experiencia de investigación-acción, de corte cualitativo, en la que se diseñaron y ejecutaron secuencias didácticas enfocadas en la resolución de problemas de la vida cotidiana y el empleo de recursos lúdicos, para que los estudiantes de secundaria desarrollen la capacidad de efectuar las operaciones matemáticas básicas, sin que recurra a la calculadora.

La metodología adoptada está basada en el tipo de estudio investigación acción, la cual según Torrecillas y Javier (2011):

se utiliza para describir una familia de actividades que realiza el profesorado en sus propias aulas con fines como: el desarrollo curricular, su autodesarrollo profesional, la mejora de los programas educativos, los sistemas de planificación o la política de desarrollo. Estas actividades tienen en común la identificación de estrategias de acción que son implementadas y más tarde sometidas a observación, reflexión y cambio. Se considera como un instrumento que genera cambio social y conocimiento educativo sobre la realidad social y/o educativa, proporciona autonomía y da poder a quienes la realizan. (p. 3)

La elección de este tipo de metodología se sustenta en que no solo se estudia una problemática, sino que también permite un proceso continuo de búsqueda de solución mediante la acción. Además, conduce a que tanto los docentes como los estudiantes involucrados realicen una toma de conciencia y decisiones para mejorar su realidad educativa.

De acuerdo con Taylor y Bogdan citado por Quecedo y Castaño (2002, p. 20) “la investigación cualitativa es aquella que produce datos descriptivos: las propias palabras de la persona, habladas o escritas y la conducta observable”.

La ejecución de esta investigación se realizó en el Liceo Secundario Profesor Virgilio Casilla Minaya, ubicado en Los Alcarrizos, Santo Domingo, República Dominicana, en el periodo de noviembre 2018 hasta mayo 2019. La muestra seleccionada de forma intencional estuvo compuesta por 33 educandos de sexto de secundaria, 17 alumnas y 16 alumnos, con edades entre 16 y 21 años, y la docente encargada del mismo grado.

La investigación-acción se desarrolló en cuatro fases: diagnóstico, planificación, implementación y evaluación. A continuación, se presentan las técnicas e instrumentos utilizados en cada una de ellas:

Fase diagnóstica: para conocer las necesidades que presentaban los estudiantes en el área de matemáticas, se utilizaron tres técnicas: la observación no participante, una entrevista no estructurada aplicada a la docente encargada del aula y un grupo focal con preguntas abiertas al estudiantado. A raíz de la necesidad identificada, se elaboró una prueba diagnóstica, para identificar el nivel de dificultad de los estudiantes con respecto a las operaciones matemáticas. Dicha prueba contenía ocho ítems en total: siete ejercicios para efectuar operaciones: adición, sustracción, multiplicación, división y orden de efectuar las operaciones sin utilizar paréntesis; y un problema de la vida cotidiana que requería aplicar dichas operaciones para resolverlo.

En adición, se realizó una actividad que sirvió para conocer más a los estudiantes: “la cápsula del tiempo”, la cual, consistió en que los alumnos escribieran una carta a su “yo del futuro”, expresando sus expectativas con relación a sus aprendizajes esperados. Al finalizar la intervención, ellos volverían a leer sus cartas para realizar una autoevaluación.

Fase de planificación: a partir de los resultados arrojados por la prueba diagnóstica, se diseñaron secuencias didácticas que incluyeron talleres, juegos, evaluaciones, un teatro de aprendizajes, retroalimentaciones y socializaciones de los resultados de los talleres. Empezando a trabajar con la adición y sustracción, luego con la multiplicación, y por último, la división. Para organizar los contenidos se crearon dos unidades de aprendizaje, y a partir de las mismas fueron elaboradas planificaciones diarias para desarrollar las acciones. Las plantillas empleadas para realizar las planificaciones fueron las propuestas por el Ministerio de Educación de la República Dominicana (MINERD).

Fase de implementación: se ejecutaron diecisiete actividades que seguían la secuencia didáctica planificada; cuatro talleres de aprendizaje por descubrimiento, un taller de reflexión sobre los aprendizajes, cuatro retroalimentaciones de los talleres, cinco juegos didácticos, un teatro de aprendizajes, una evaluación y una retroalimentación de esta. Las mismas se llevaron a cabo un día por semana, en un espacio que gestionó la coordinación del centro, convirtiendo el proyecto en parte de la clase de la sección de estudiantes con la que se trabajó. Las actividades tuvieron una duración de 90 minutos cada una, en un período de 5 meses (diciembre 2018-mayo 2019). A continuación, se describen algunas de las ellas:

1. Talleres de aprendizajes por descubrimiento y colaborativo, orientados a que los alumnos construyan las definiciones de las distintas operaciones y a la deducción de sus propiedades, partiendo de la manipulación de objetos, la realización de tareas y sus aprendizajes previos. Se ejecutaron un total de cuatro talleres, cada uno con una duración de 90 minutos. Los talleres implicaron ocho semanas de trabajo. Cada taller contenía un documento escrito con una serie de preguntas y actividades de exploración a realizar por los estudiantes, con la finalidad de realizar conjeturas y construir la definición de las operaciones. Luego, tenían que efectuar operaciones que enlazaban a la deducción de sus propiedades, y finalmente, resolver problemas matemáticos adaptados a su contexto, donde debían aplicar la operación trabajada. En cada encuentro se realizó una puesta en común, en la que los estudiantes presentaban sus respuestas, se corregían de forma coevaluativa sus errores y se llegaban a conclusiones generales.
2. Juegos educativos, se realizaron en cada encuentro posterior a la retroalimentación de un taller para evaluar y consolidar los conocimientos adquiridos por los estudiantes. La mayoría de estos fueron versiones de juegos de mesa comunes como; Dominó, Rompecabezas y Parchís, a los que se les modificaron las reglas originales y se les agregaron mandatos, para que directa o indirectamente, ellos tuvieran que efectuar operaciones, y con esto, alcanzar el objetivo de la actividad: afianzar los aprendizajes de las operaciones correspondientes, de forma significativa.
3. Un teatro de aprendizaje, en el que los alumnos expusieron, de manera creativa y artística, lo que habían aprendido de las operaciones matemáticas básicas durante las actividades desarrolladas, con el propósito de que ellos perciban otra forma de presentar sus aprendizajes. Por cada actividad los/as estudiantes redactaron sus correspondientes diarios reflexivos.

Fase de evaluación: se utilizó la técnica de entrevista a profundidad a la docente de matemáticas. El motivo de esta entrevista fue conocer la opinión de ésta con relación a la aplicación del proyecto y los cambios observados de los educandos en el dominio de las operaciones matemáticas básicas durante sus clases, sin utilizar calculadora. También, se aplicó una prueba de evaluación final a los y las estudiantes, en la cual se tomaron en cuenta ejercicios similares a los de la prueba diagnóstica, esto permitió que se pudieran comparar los resultados. Por último, se tuvo un último encuentro con el estudiantado, en el cual expresaron las expectativas que se cumplieron con respecto al proyecto.

Por otro lado, en la presentación de las categorías y en el análisis de datos se incorporaron frases textuales de los estudiantes. Los mismos fueron nombrados como “Sujeto A, B, C…”, para proteger su identidad.

4. Resultados

A continuación, se presentan y se describen los resultados obtenidos por fases. Los datos se analizaron a través de categorías, las cuales se crearon a partir de las respuestas más comunes de los estudiantes. En el proceso, algunas categorías fueron eliminadas porque fueron poco notables o menos frecuentes. Se realizó la triangulación entre los datos procedentes de las distintas fuentes y técnicas utilizadas.

4.1. Diagnóstico Inicial

En la etapa de diagnóstico se utilizaron las siguientes técnicas de recolección de datos para detectar las necesidades de los escolares: entrevista no estructurada, grupo focal y prueba diagnóstica. Además, se realizó una actividad que ayudó a conocer a los estudiantes; “la cápsula del tiempo”.

Por otro lado, la entrevista realizada a la docente aportó un punto de partida para conocer las dificultades que estaban afectando el aprendizaje de los y las estudiantes en el área de matemáticas. En palabras de la docente “la mayoría de los estudiantes no sabe realizar las operaciones matemáticas básicas sin el uso de la calculadora”, y además, destacó su importancia diciendo, “Cuando estoy trabajando temas de álgebra, geometría y otros más, tengo que dejar el contenido curricular y volver a explicarles las operaciones básicas y eso me cuesta tiempo”, lo que implica que para entender y profundizar en otros contenidos del área es necesario conocer las operaciones básicas y tener al menos una noción del proceso para resolverlos.

En el grupo focal con estudiantes, se realizaron preguntas como las siguientes: ¿cuáles dificultades se les han presentado en temas de matemáticas? ¿En cuáles temas o contenidos dentro de las matemáticas se les dificulta el aprendizaje? ¿Saben resolver suma, resta, multiplicación y división sin calculadora? ¿Esa dificultad, les puede traer problemas en otros temas de matemáticas? ¿Están de acuerdo que trabajemos con ese contenido? En las respuestas de los estudiantes se hizo visible su perspectiva hacia las matemáticas, pues contestaron “las matemáticas completas son un problema”, “no sabemos trabajar con fracciones”, “no sabemos multiplicar”, “con las matemáticas no se compra en el colmado”, “no sabemos dividir”, “no me gustan las matemáticas”, “es la asignatura más difícil”, “resolvemos las operaciones con la calculadora”, “la trigonometría no me entra”; y en cuanto a si sabían efectuar operaciones básicas, la gran mayoría respondió al unísono “ no”. Además, los que respondieron que sí estaban interesados en ver otras formas de aplicarlas “sí, pero me gustaría conocer otros usos y formas de aprenderlas”.

A partir de las observaciones realizadas en el aula, las respuestas de la docente y de los resultados obtenidos en el grupo focal; se tomó la decisión de trabajar con la necesidad de efectuar operaciones matemáticas básicas sin utilizar la calculadora, puesto que dominar las operaciones representa parte fundamental de lo que los estudiantes necesitan para desarrollar las competencias del curso en que están; los preparan para entender contenidos que necesitan para aprobar las pruebas estandarizadas, tanto nacionales como internacionales, y las seguirán utilizando en su vida universitaria y profesional. Lo más importante es lograr que los estudiantes sean personas competentes, capaces de razonar y resolver problemas en sus contextos utilizando las matemáticas de forma consciente.

Posteriormente, para identificar el nivel de dominio de las operaciones matemáticas básicas por parte de los educandos, se implementó una prueba diagnóstica creada por los investigadores. Los resultados de dicha prueba están mostrados en la siguiente tabla, en la cual se especifican las frecuencias que los estudiantes obtuvieron en cada categoría:

1. Respuestas y procedimientos correctos (RPC)
2. Respuestas y procedimientos incorrectos (RPI)
3. Respuestas incorrectas y procedimientos correctos (RIPC)
4. Sin respuestas (SR)

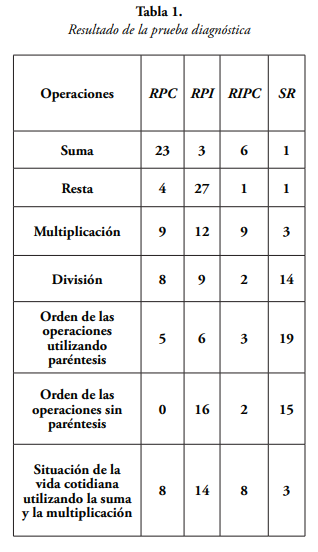
Al observar la cantidad de estudiantes que obtuvo respuestas correctas efectuando las operaciones aritméticas, se decidió trabajar con un eje puesto en el desarrollo de competencias que involucren dichas operaciones, aun siendo estas competencias para grados menores.

La última actividad diagnóstica fue la cápsula del tiempo, dirigida a los educandos, luego de presentarle los objetivos y la metodología con la que se iba a trabajar, con el propósito de conocer sus expectativas ante el proyecto y el impacto que puede tener en ellos y en su futuro como estudiantes. Los resultados están organizados en dos categorías, como se muestra en la tabla 2:

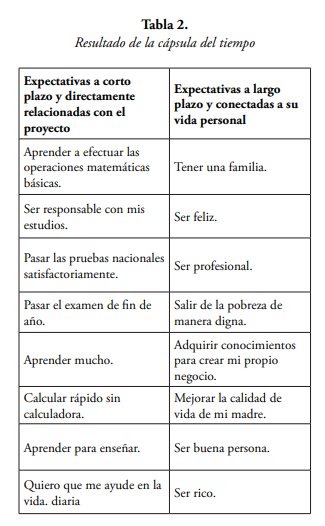
Posteriormente se presentan algunos fragmentos textuales de las cartas escritas por los y las estudiantes.

Sujeto A: “yo quiero en el futuro aprender a hacer mis cálculos sin calculadora. quiero ser bueno en eso porque me va a ser útil en la vida, me ayudará mucho en mi trabajo, en mi quehacer, en todo mi alrededor”.

Sujeto B: “mi yo del futuro, si Dios quiere se me de todo lo que pienso, es que quiero terminar mis estudios, ser profesional, tener mi propia empresa, casarme con la mujer que amo, viajar junto a ella, tener una hermosa familia y ser feliz porque la vida se trata de momentos y quiero trabajar y vivir como para que mis generaciones estén bien.”

Sujeto C: “... quiero lograr todas mis metas como hacer mi carrera de ingeniería y graduarme, tener un trabajo, vivir bien, poner a mi madre a vivir como una reina. y también me gustaría ser un ingeniero famoso reconocido en el mundo entero.” 

En estas expresiones se pudieron apreciar los intereses, motivaciones, metas y propósitos de los sujetos con relación al proyecto y sus planes futuros. Además, de esta manera ellos mencionaron cómo esperaban que fueran las actividades: divertidas, lúdicas, que contengan más que solo las operaciones y que estuvieran directamente relacionadas con su vida cotidiana y la aplicación a distintas profesiones. 

Por otro lado, conocer y leer sus expectativas respecto a cómo esperaban que este proyecto marque sus vidas generó una voluntad de compromiso, mucha responsabilidad y motivación al trabajar con ellos y ellas. Esta actividad ayudó a conocerlos más a profundidad, es decir, sus contextos y metas, y a partir de esto se identificaron las estrategias más factibles para que ellos aprendan y la manera de conducir las actividades.

4.2. Implementación

A continuación, se evidencian los resultados de algunas de las actividades desarrolladas con los estudiantes para que estos alcancen el objetivo. En estas actividades estuvieron los talleres de aprendizaje por descubrimiento, que incluyeron ejercicios de aplicación en la vida cotidiana, los juegos educativos y los diarios reflexivos.

Se realizaron un total de cuatro talleres de aprendizaje por descubrimiento. La elaboración y aplicación de estos fueron bajo procedimientos similares, por eso, solo se van a plasmar los resultados del taller de la adición como referencia. En este taller los estudiantes estuvieron divididos en grupos de trabajo de cuatro participantes y tenía varios momentos a trabajar.

En un primer momento, se realizó una recuperación de saberes previos de los estudiantes, para conocer lo que recordaban sobre el sistema de numeración decimal, y mediante el uso de un tablero con tapas plásticas se les explicó que cada 10 unidades se convertían en una decena, cada 10 decenas en una centena, y así sucesivamente. Luego, en un segundo momento se les entregaron unas hojas que contenían por escrito 6 ítems, que consistían en: escribir el valor posicional de un número, descomponer números en sumas de unidades, contar y agrupar objetos cotidianos (luego decir cuál era la cantidad total de objetos), efectuar sumas, asociar palabras con la adición (ganar, subir, positivo, agregar, aumentar…), dar una definición con sus palabras de lo que entendían que era adición y por último, un problema de aplicación relacionado con su contexto escolar.

Durante el desarrollo del mencionado taller, los estudiantes discutieron entre ellos las respuestas que consideraban correctas y completaron cada ítem partiendo de razonamientos realizados en los ítems anteriores. Estos tenían libertad de hacer preguntas a los investigadores y la docente, cuando no entendían algún ítem. Los investigadores y la docente se mantenían monitoreando a los estudiantes para cerciorarse de que todos estuvieran trabajando.

Las competencias trabajadas en todas las actividades de la intervención se describen a continuación.

• Razona y argumenta: comprende el significado de las diferentes operaciones con números enteros (adición, sustracción, multiplicación y división), utilizando diferentes estrategias para resolverlas. Aplica propiedades de las distintas operaciones para realizar cálculos. Justifica sus procesos de razonamiento utilizando las propiedades de las operaciones aritméticas y las del sistema de numeración decimal.
• Modela y representa; representa situaciones matemáticas y cotidianas utilizando operaciones aritméticas con números enteros.
• Conecta: utiliza las operaciones aritméticas para resolver problemas en otras áreas o ramas de la matemática, en otras disciplinas del saber y en la vida cotidiana.
• Resuelve problemas: resuelve problemas en contextos diversos utilizando la o las operaciones apropiada(s).

Al analizar las respuestas de los educandos en los ítems del documento escrito de los talleres de aprendizaje por descubrimiento, de la adicción surgieron tres categorías: definición de la adición, errores al efectuar las operaciones y respuestas distintas al ejercicio de la vida cotidiana.

• Definición de adición

En esta categoría surgieron tres subcategorías o respuestas más comunes dadas por los grupos: 

Es la suma de dos cantidades. Es cuando se saca el total de los sumandos. Es como añadir una cosa a otra, adquiriendo un nuevo valor mayor al que tenía.

A continuación, se muestran algunas respuestas textuales que colocaron los estudiantes:

Grupo A: “Es cuando se saca el total de los sumandos”.

Grupo B: “La adición es lo que se suma y nos da como resultado del sumando donde buscamos la suma o total”.

Grupo D: “Para nosotros es adquirir algo que no tenemos como, por ejemplo: Que tenga 100 pesos y me regalan 50 tendré 150 pesos”.

Grupo E: “Es como añadir y agregar una cosa a otra”.

Luego de revisar las respuestas de los escolares, en la clase posterior se realizó una retroalimentación del taller, en esta todos los grupos expresaron su definición, luego las compararon con la definición del libro de texto dada por los investigadores, y se construyó una no muy alejada a la dada por Sotillo (2013): la adición también llamada suma, consiste en añadir o agregar una cantidad a otra para obtener un resultado total. Sus elementos son: los sumandos, la suma o total y el signo.

• Errores comunes al realizar las distintas operaciones

En los siguientes párrafos se analizaron los errores más comunes que cometieron la gran mayoría deeducandos al efectuar las operaciones matemáticas básicas en los talleres de todas las operaciones: 

1. Errores en la adición: colocar el resultado de las sumas parciales sin realizar los reagrupamientos correspondientes.
2. Errores en la sustracción: si la cifra en el minuendo es menor que su correspondiente en el sustraendo restar al revés, es decir, restar el minuendo al sustraendo, mal interpretación del ejercicio para traducirlo al lenguaje numérico, confundir el nombre de los elementos.
3. Errores en la multiplicación: multiplicar un número por cero y colocar como resultado el mismo número, cuando se tiene que “llevar” un número, en lugar de reagrupar las decenas y colocar las unidades realizarlo de manera inversa; No dejar el espacio correspondiente al valor posicional al momento de multiplicar con más de un dígito y no efectuar las sumas parciales de manera correcta.
4. Errores de la división: si la división no era exacta, colocar un 0 antes del punto que indicaba el decimal, mal interpretación de lo que se le pidió en el ejercicio; no comprender cómo expresar un problema de la vida cotidiana en forma de división; desconocieron el nombre de los elementos de la división; no efectuar bien las multiplicaciones parciales; realizar de manera incorrecta las restas.

Durante la retroalimentación que se realizaba después de cada taller, se resolvían todos los ejercicios de este, pero haciendo más énfasis en los ejercicios que se cometieron errores, elaborando preguntas reflexivas y discutiendo las respuestas desde un razonamiento crítico y participativo. Asimismo, si algún estudiante volvía a cometer los mismos errores, uno de los investigadores le explicaba de manera individual, mientras los demás seguían presentando sus respuestas en la puesta en común.

Dentro de los grupos de trabajos colaborativos, algunos estudiantes se mostraron con actitudes negativas de trabajar, por lo que dejaban el desarrollo del taller en manos de sus compañeros que comprendían mejor las operaciones, dificultando esto el objetivo de que todos participen y aprendan unos de otros. En estos casos se hizo necesaria la intervención de la docente, quien recordó y enfatizó las reglas del trabajo en aula.

Al utilizar la estrategia de aprendizaje por descubrimiento, a la gran mayoría de los alumnos les resultó difícil de comprenderla, se preguntaban y decían: “¿Para qué estamos haciendo esto?” “¿A dónde vamos a llegar?” “Esto es muy infantil”. En general, no utilizaban un razonamiento crítico y deductivo para formar sus ideas, muchos solo reescribieron lo que ya se le había dado y no entendían, no obstante, con el tiempo se fueron adaptando y empezaron a sacar sus propias conjeturas y conclusiones, despertando la capacidad de asombro y la noción de que ellos son capaces de argumentar y conceptualizar.

• Problemas de la vida cotidiana

En los problemas de la vida cotidiana los estudiantes mostraron un mejor dominio de las operaciones matemáticas básicas que en los ejercicios planteados para resolver la operación. En ocasiones, los escolares tenían dificultades para resolver algunos ejercicios, sin embargo, cuando se enfrentaban a uno similar que involucraba su contexto, lo hacían con resultados satisfactorios.

Para estos problemas utilizaron distintas estrategias, no solo la forma convencional de resolver dichos ejercicios, puesto que en preguntas donde era necesario realizar multiplicaciones, el 37.5 % de los estudiantes efectuaban la suma repetidas de las cantidades o intuían la respuesta por tanteo y error, lo que revela que cada persona realiza su propia interpretación de la misma situación cotidiana. Una pregunta donde esto se evidencia es la siguiente:

Edwin, Esmeralda y Estefany quieren hacer un locrio de salami en la casa de Michelle, para esto, necesitan cuatro libras de arroz, y dos libras de salami. La libra de arroz cuesta 22 pesos, y la libra de salami está a 85 pesos. Si en los demás ingredientes van a gastar 57 pesos, ¿cuánto dinero necesitan en total?, tomando en cuenta todos van a contribuir con la misma cantidad de pesos, ¿Cuánto dinero tendrá que aportar cada persona?

La respuesta más directa sería multiplicar las libras de los productos por el precio correspondiente, luego sumar los 57 pesos que corresponden a los demás ingredientes; y el resultado dividirlo entre el número total de personas. Sin embargo, surgieron procedimientos distintos, como sumar el precio cuantas veces decía las libras, y luego sumar los 57 pesos, o tomar una cantidad de dinero próxima a la correcta e ir realizando las operaciones para aproximarse a la respuesta.

En el párrafo anterior, el procedimiento realizado por estos estudiantes no es incorrecto, pero es una interpretación muy básica de trabajar con la multiplicación, pues para el grado en que se encontraban los educandos debieron trabajar con el algoritmo que implica la misma. Sin embargo, esto pone en evidencia su comprensión de la multiplicación como una suma repetida de sumandos iguales, que fue uno de los conceptos trabajados en clase. La siguiente imagen muestra un ejemplo textual de la respuesta de un grupo de estudiantes a una pregunta relacionada con su vida cotidiana, donde se confirma lo mencionado.

• Juegos educativos

Los juegos fueron elaborados de una manera que los estudiantes puedan identificar similitud con otros juegos de mesa convencionales, intentando mantener su interés, para que lo disfrutaran mientras reforzaban su aprendizaje. Dentro de la variedad de juegos, algunos eran con formas y estrategias totalmente nuevas, y otros, eran similares a los que ya ellos conocían, los cuales, sin importar el tipo, estaban directamente relacionados con las operaciones matemáticas básicas. Antes de jugar conocieron algunas ideas claves de las operaciones, las cuales les permitieron comprender el sentido de los juegos. Cabe destacar, que algunos estudiantes no se mostraron tan motivados a jugar, puesto que les parecían un poco aburridos o aún no dominaban los conceptos que estos evaluaban. 

Se ejecutaron un total de 6 juegos: dominó a la americana, la tabla de multijugar, el operandi andante, rompecabezas de la división, cuadrados mágicos y el dadocaedro de los resultados. A continuación, se presentan un ejemplo de los juegos utilizados:

En este juego cada estudiante tenía su propia ficha y avanzaba lanzando un dado. La regla principal es que en la casilla dónde llega la ficha con el número de pasos que indica el dado, el jugador debe decir el resultado de la multiplicación de la fila por la columna correspondiente, si no responde correctamente; retrocede a la casilla que estaba antes de lanzar el dado.

Este mismo tablero se utilizó para el juego El dadecaedro de los resultados, pero con reglas distintas. En este, el dado no era uno estándar sino un dodecaedro construido con papel Fabriano, en cuyas caras había operaciones para resolver. El resultado de dicha operación indicaba cuántas casillas avanzar.

Se realizaron varios rompecabezas de este tipo con el fin de dar a entender el algoritmo y los elementos de la división.

El juego “El operandi andante” consiste en un tablero con un camino, en el cual los estudiantes, a medida que avanzan la cantidad de pasos que indica un dado, tienen que resolver operaciones cada vez más complejas que estaban escritas en las casillas. Para la implementación del mismo, se utilizó una música de fondo atendiendo a los estilos de aprendizaje de los estudiantes, e intentando darle más vida a la clase. Se fueron colocando canciones de su preferencia y relacionadas a la cultura general, puesto que esta actividad se desarrolló en horario de la tarde después del almuerzo; momento en que los y las estudiantes suelen estar un poco cansados. Además, era una manera de mantener la clase relajada y activa. Esta actividad les resultó muy llamativa a los estudiantes, porque mientras jugaban y escuchaban música aprendían matemáticas y no se sentían que estaban dentro de un aula de clase.

• Diarios reflexivos de apuntes

Los diarios de apuntes sirvieron para conocer lo que aprendieron los estudiantes en cada actividad, ellos expresaron cómo se sintieron en el proceso de enseñanza, cómo valoraron su participación en la clase, qué cosas diferentes no conocían de las operaciones, evaluaron las estrategias utilizadas y las cosas que se podían mejorar en el proyecto.

Al principio varios estudiantes se mostraron renuentes a escribir el diario de apuntes, por estereotipos de género, pues lo veían como una actividad designada para féminas, pero en el transcurso del tiempo y al observar cuál era el objetivo de este, empezaron a hacerlo. Otros escribían en sus diarios sólo para cumplir con el requerimiento y no reflejaban lo que en realidad sentían, cuando se detectó esto, se hizo una devolución de los diarios para que lo escribieran nuevamente.

A continuación, se muestra un ejemplo de apuntes de los estudiantes en su diario. Los mismos, giraban en torno a responder tres preguntas metacognitivas: ¿qué aprendí? ¿para qué me sirve?, ¿cómo me sentí?

Sujeto F:

Aprendí que el orden de los factores no altera el producto. Lo que aprendí hoy sirve para todo lo que haga en el diario vivir.” “Siento con un dolor insoportable, porque cometí un error con la persona equivocada.”

Sujeto G:

“Aprendí a sumar nuevamente y que haga lo que haga, la división no me entra.” 

Sujeto H:

“…Hoy aprendí que la matemática puede ser divertida dependiendo de quién te la de o como la expliqué, también aprendí que puedo aprender mientras me divierto.”

4.3. Resultados evaluación final

Para la evaluación final, los estudiantes recibieron una prueba con ejercicios y problemas similares a los de la prueba diagnóstica. La siguiente tabla muestra los resultados de dicho examen, se utilizaron las mismas categorías que la prueba diagnóstica para obtener una visualización más amplia de los avances que tuvieron los mismos.

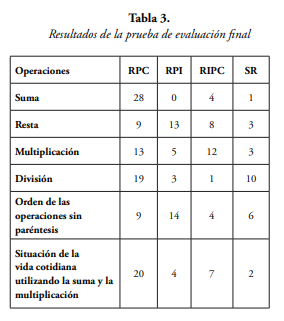
Comparación de los resultados encontrados en la prueba diagnóstica y en la prueba final

En el gráfico 1 se evidencia de manera más visible el progreso de los alumnos en cuanto a las operaciones matemáticas básicas. En las barras de la izquierda se observan los resultados de la prueba diagnóstica correspondientes a las categorías previamente descritas; y en las barras de la derecha, los resultados de la prueba final. Obsérvese que las barras azules correspondientes a respuestas y procedimientos correctos aumentaron, mientras que las barras rojas correspondientes a respuestas y procedimientos incorrectos disminuyeron. Además, las barras amarillas correspondientes a “sin respuesta” disminuyeron considerablemente, lo que da a entender que más estudiantes tenían confianza en poder responder los ítems.

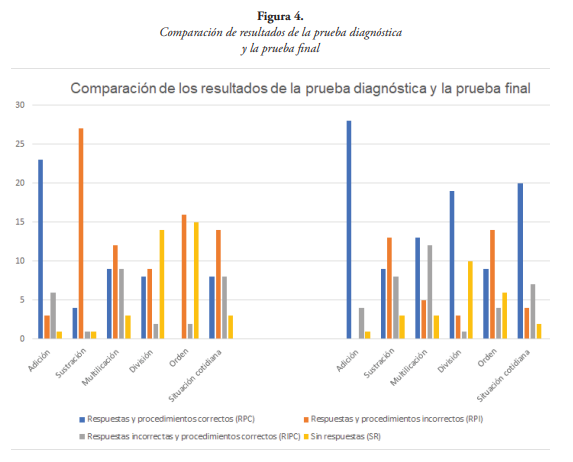
Es evidente el gran avance que tuvieron los estudiantes después de observar los resultados de la prueba final y hacer una comparación con la primera prueba que fue aplicada, pues el número de respuestas vacías disminuyó, además que demostraron un mayor nivel de seguridad a la hora de resolver los ejercicios y problemas.

Evaluando la categoría Respuestas y Procedimientos Correctos (RPC), en la adición pasó de un 69.7 % a un 84.85 %, aumentando 15.15 %. En la sustracción el cambio fue de un 12.12 % a un 27.27 %; aumentando un 15.15 %; mientras que en la multiplicación pasó de un 27.27 % a un 39.39 %, con un incremento de un 12.12 %. En la división pasó de un 24.24 % a un 57.58 %, con un aumento significativo de 33.34 %. Asimismo, en el orden pasó de un 0% a un 27.27 %, en tanto que en la situación de la vida cotidiana cambió de un 24.24 % a un 60.61 %, aumentando un 36.37 %. En promedio, la cantidad de estudiantes que obtuvieron tanto la respuesta como el algoritmo correcto para todas las operaciones aumentó en un 23.23 %, obteniendo los mejores resultados en la división y en la solución de problemas de la vida cotidiana.

Del mismo modo, la categoría Respuesta y Procedimiento Incorrecto (RPI) en la adición pasó de un 9.09 % a un 0 %. En la sustracción cambió de un 81.82 % a un 39.39%, disminuyendo un 42.43 %. En la multiplicación pasó de un 36.36 % a un 15.15 %, con una disminución de 21.21 %, mientras que en la división varió de un 27.27 % a un 9.09%, disminuyendo un 18.18 %. En el orden, pasó de un 48.48 % a un 42.42 %, con una reducción de un 6.06 %; y en el problema de la vida cotidiana varió de un 42.42 % a un 12.12 %, disminuyendo un 30.3 %. En promedio, esta categoría, muestra la cantidad de estudiantes que obtuvo tanto la respuesta como el procedimiento erróneo, obteniendo una reducción de un 21.21 %, donde el mayor cambio fue en la operación sustracción.

Por otro lado, en la categoría Respuestas Incorrectas y Procedimiento Correcto (RIPC); en la adición pasó de un 18.18 % a un 12.12 %, disminuyendo un 6.06 %; mientras que la sustracción cambió de un 3.03 % a un 24.24 %, aumentando un 21.21 %. De igual modo, en la multiplicación pasó de un 27.27 % a un 36.36 %, con un aumento de 9.09 %; en tanto que la división pasó de un 6.06 % a un 3.03 %, disminuyendo un 3.03 %. En el orden varió de un 6.06 % a un 12.12 %, aumentando un 6.06 %. Finalmente, en el problema de la vida cotidiana cambió de un 24.24 % a un 21.21 %, disminuyendo un 3.03 %. Esta categoría muestra cuántos estudiantes obtuvieron una respuesta incorrecta, pero con un procedimiento parcialmente correcto, mostrando que al menos conocían los algoritmos de las operaciones, obteniendo aumentos (estudiantes que antes habían realizado tanto el procedimientos como la respuesta de forma errónea, ahora por lo menos conocían el procedimiento) y bajas (estudiantes que antes sólo conocían el procedimiento, ahora también conocían las respuestas correctas, por lo que pasaron a RPC). En sentido general el promedio de respuesta a esta categoría aumentó un 24.24 %.

En cuanto a la categoría sin respuestas (SR), en la adición se mantuvo igual con un 3.03% en ambas pruebas; en la sustracción cambió de un 3.03 % a un 9.09 %, aumentando un 6.06%, mientras que en la multiplicación se mantuvo con un 9.09 %. Por otro lado, en la división pasó de un 42.42 % a un 30.3 %, disminuyendo un 12.12 %. En el orden pasó de un 45.45 % a un 18.18 %, disminuyendo un 27.27 %; y en el problema de la vida cotidiana varió de un 9.09 % a un 6.06 %, disminuyendo un 3.03 %. El promedio de respuestas a esta categoría disminuyó en un 36.36 %, lo que evidencia que menos estudiantes dejaron preguntas sin respuestas, en especial, las relacionadas con el orden de las operaciones y la división, las cuales, fueron donde se obtuvo más respuestas vacías en el diagnóstico.

Cabe destacar que los estudiantes lograron mejores calificaciones en los últimos contenidos trabajados, a pesar de ser más complejos. El comportamiento de los estudiantes y su desempeño en el aula muestra un aumento de dominio aún mayor que el que expresa la prueba, lo que lleva a pensar que hay factores que influyen en el desempeño de los estudiantes al momento de tomar un examen, de manera que impiden que estos den lo mejor de sí. Además, los investigadores retroalimentaron la prueba final y discutieron los resultados con los participantes, aquellos cuyo dominio fue mínimo se les dieron algunas correcciones y retroalimentaciones de manera individual, exhortándolos a seguir mejorando su dominio de las competencias trabajadas.

Por otra parte, se le aplicó una entrevista semiestructurada a la profesora de matemáticas encargada del aula. Las preguntas realizadas a la docente estaban orientadas a sí notó cambios significativos generados como producto de la implementación del proyecto, a su opinión respecto a las estrategias y recursos utilizados, y al manejo en el aula de los investigadores. En cuanto a las mejoras en el grupo estudiantil, la más destacada por la docente en la entrevista fue que en sus clases los estudiantes disminuyeron el uso de la calculadora, además, luego de mostrarle cuál era el objetivo general de la investigación, afirmó que sí se cumplió, y que estaba conectado a las estrategias y recursos utilizados. Respecto a estos últimos dos aspectos, la docente añadió que les sirvieron como referencia para otras actividades: “voy a utilizar el tema de ‘Jugando se aprende’ (para una feria escolar de ciencias), porque ustedes le demostraron que jugando se aprende y que las operaciones matemáticas las podían dominar más de esa manera.”

Por último, en relación con el manejo en el aula y la didáctica del equipo investigador la docente expresó: “Ustedes se han manejado muy bien... están listos para ser maestros de excelencia”. 

Conclusiones

El presente trabajo buscó presentar una experiencia de investigación acción, de corte cualitativo, en la que se diseñaron y ejecutaron secuencias didácticas enfocadas en la resolución de problemas de la vida cotidiana y el empleo de recursos lúdicos, para que los estudiantes de secundaria desarrollen la capacidad de efectuar las operaciones matemáticas básicas sin la necesidad de utilizar la calculadora.

Los resultados del diagnóstico evidencian que estudiantes de sexto de secundaria tenían dificultades en la comprensión de nuevos contenidos matemáticos, a causa de un dominio deficiente de las operaciones matemáticas básicas, un rechazo a esta asignatura y una dependencia de la calculadora. Para contrarrestar este problema, se elaboraron secuencias didácticas basadas en las estrategias pedagógicas que plantea el currículo dominicano. Al implementar estas secuencias fueron identificados los errores que cometía el estudiantado al efectuar las operaciones, a través de las retroalimentaciones. Además, entre las estrategias utilizadas, la resolución de problemas y el uso de juegos educativos facilitaron en los estudiantes el desarrollo de competencias matemáticas y la independencia de la calculadora. 

El uso de la estrategia de resolución de problemas del contexto permite a los estudiantes comprender mejor las operaciones matemáticas básicas y darle sentido, puesto que confirman la importancia y el uso continuo de estas en su entorno. Además, cuando los estudiantes se sienten involucrados, ya sea porque su nombre está en el problema planteado o porque es una situación por la que ha pasado recientemente, aumenta su motivación e interés por el aprendizaje. Esto reafirma conclusiones de investigaciones en Chile (Bahamondes y Vicuña, 2011), México (Mastachi, 2015) y Colombia (Cárdenas y González, 2016; Vargas y Stinfen, 2018); quienes plantean que la resolución de problemas, siguiendo los pasos de Pólya (1945), beneficia el nivel de razonamiento matemático en los estudiantes.

En otro orden, el aprendizaje por descubrimiento es una estrategia actual en las aulas dominicanas. Los estudiantes desconocen de la misma y en principio les resulta difícil dirigir y gestionar su propio aprendizaje, sacar conclusiones y además, les genera muchas inquietudes respecto al desarrollo de los talleres, lo que implica una ardua labor para los docentes, porque los estudiantes necesitan de alguien que los guíe en la misma medida que les de autonomía, lo que requiere de un proceso adaptativo. Esto concuerda con Machaca y Samo (2018), quienes plantean que esta estrategia influye significativamente en el rendimiento académico en el área de matemática en los estudiantes, aunque al inicio estos se muestren apáticos con respecto a su propio aprendizaje.

En República Dominicana, una investigación sobre las estrategias de aprendizaje de las matemáticas (Holguín, 2016) sugiere que los docentes consideren el uso de recursos para la observación y manipulación. Los juegos pueden convertirse fácilmente en ese tipo de recursos y estar orientados tanto a la evaluación como a la deducción de un aprendizaje nuevo. Además, pueden cambiar la perspectiva del estudiantado con respecto a las matemáticas, como lo expresa uno de los sujetos de este estudio: “hoy aprendí que la matemática puede ser divertida dependiendo de quién te la de o como la explique, también aprendí que puedo aprender mientras me divierto” (Sujeto H) en un diario reflexivo, tras un taller de juegos. Concordando con Blasco (2017), las matemáticas no tienen que ser aburridas, a través de experiencias lúdicas se pueden aprender desde edades tempranas, por tanto, sugerimos la implementación de estrategias involucren el juego para la enseñanza de las matemáticas en todos los niveles educativos.

Por otro lado, investigaciones realizadas en Argentina y México (Minnaard y del Puerto, 2002; Trigo, 2016) defienden el uso de las calculadoras y las nuevas tecnologías como una herramienta para analizar y visualizar los conceptos y relaciones, así como para ahorrar tiempo y agilizar la resolución de problemas. Contrario a esto, otros estudios realizados en Ecuador (Campos, 2013), México (López et al., 2017) y Colombia (Granados, 2019) sugieren que el uso de esta herramienta puede generar dependencia, y que antes de utilizarlas, es necesario haber desarrollado el razonamiento matemático. Luego de tener este dominio, se recomienda una buena introducción de las mismas, primero para validar resultados, y después con preguntas de análisis y razonamiento, donde las tecnologías no puedan dar todas las respuestas. Los resultados de este estudio concuerdan con ellos, puesto que los estudiantes estaban perdiendo destrezas matemáticas a raíz del uso de la calculadora, sin conciencia del procedimiento que está efectúa. 

Para concluir, se recomienda que el equipo de gestión de cada centro educativo le proporcione a los alumnos, antes de iniciar la secundaria, una prueba diagnóstica como plantea el MINERD (2016), con la finalidad de conocer el dominio que tienen estos con relación a las operaciones matemáticas básicas y contenidos afines. De esta manera, se ayuda a que cada docente esté consciente del grado de dominio de los educandos en el tema, y desde el primer año de secundaria, se pueda reforzar los mencionados contenidos.

De esta forma, los educandos tendrán una mejor comprensión en el área de las matemáticas. Por consiguiente, es importante realizar proyectos de investigación acción que involucren estas estrategias desde los grados de primaria, para que los escolares desde pequeños valoren las matemáticas, puedan resolver problemas y divertirse con ellas.

Por último, no podemos generalizar los resultados de este estudio, debido a que todos los grupos de estudiantes son distintos y se debe partir de sus intereses. Sin embargo, el aumento significativo de las respuestas y procedimientos correctos de los estudiantes, más el cambio de aptitud hacia el aprendizaje de las matemáticas, concibiéndolo como un medio para mejorar su calidad de vida y para resolver problemas de su cotidianidad; sugieren que las estrategias pedagógicas derivadas del aprendizaje por descubrimiento, el trabajo colaborativo, la resolución de problemas y los juegos didácticos son efectivas para el aprendizaje de las operaciones matemáticas básicas sin necesidad de utilizar la calculadora. Además, se recomienda realizar más investigaciones con una visión crítica sobre la influencia de la calculadora y las nuevas tecnologías en el desarrollo de competencias matemáticas y la forma de introducirlas a los estudiantes.