Aspectos históricos del teorema fundamental del cálculo y posibles mediaciones tecnológicas

1. Introducción:

La sociedad y el sector empresarial demandan que el futuro egresado sea cada vez más competente, eficaz, eficiente, capaz de lograr un aprendizaje continuo, de resolver y prever problemas, a la vez, que su formación vaya en sintonía con la capacidad de aprendizaje y adaptación a nuevas situaciones problemáticas (Capote et al., 2016; Zuñiga, 2016; Palma, 2012). Esta formación de futuros profesionales no puede ir desconectada de los avances tecnológicos y técnicos que tiene el mundo globalizado (Serna y Serna, 2015; Gorgone et al., 2010; Moreno, 2007). Tal panorama demanda el desarrollo de nuevas competencias didácticas en el profesorado. Es así como los formadores no deben ser únicamente transmisores de conocimientos, sino además, deben orientar y ayudar a construir procesos que permitan aprender a aprender y aprender a emprender, es decir, enseñar a comprender e interpretar, transformando la información en conocimientos, así como potenciar la creatividad y la resolución de problemas (Najwa et al., 2018; Capote et al., 2016).

Estas exigencias también plantean retos en la formación de futuros profesionales, porque desarrollar y evaluar las competencias necesarias son tareas complejas que exigen al profesor una formación muy calificada. En efecto, “el desarrollo del pensamiento y de las competencias matemáticas de los alumnos depende de manera esencial de la formación de sus profesores” (Font, 2011, p. 11). Dado que se consideran las matemáticas como una de las ciencias básicas en los currículos de ciertas carreras universitarias, éstas tienen un papel fundamental en la formación.

En este contexto, es necesario aportar conocimiento sobre cómo la enseñanza de las matemáticas, como una ciencia básica, puede ayudar a demandas tan ambiciosas como, por ejemplo, la de formar profesionales que puedan aprender a aprender de por vida (Capote León et al., 2016). Es preciso entonces que el profesor tenga un cierto nivel de competencia, es decir, “ha de conocer y ser capaz de realizar las prácticas matemáticas necesarias para resolver los problemas matemáticos usualmente abordables por los estudiantes del nivel correspondiente, y debe saber articularlos con los bloques temáticos posteriores” (Godino et al., 2017, p. 91).

Como eje central de las matemáticas en los currículos, aparecen las asignaturas de cálculo (análisis matemático real o complejo), y entre sus muchos objetos matemáticos importantes, existe el Teorema Fundamental del Cálculo (TFC), “una piedra angular adecuada para cualquier desarrollo riguroso del cálculo” (Dunham, 2005, p. 105). Dicho esto, proponer cambios en los procesos de enseñanza y aprendizaje del TFC, incidiría, tanto en estudiantes como en docentes, en la comprensión de objetos matemáticos posteriores: Teorema de Green, Teorema de Stockes, Teorema de la Divergencia, cálculo de probabilidades para variables aleatorias continuas, resolución de ecuaciones diferenciales e integrales, la transformada de Laplace, etc.

Entre los inconvenientes que existen con estos procesos de enseñanza y aprendizaje del TFC se conocen, por ejemplo, del lado de los docentes, que algunos de ellos tienen un bajo conocimiento conceptual, incluso a veces procedimental, de la integral definida (Rosyidi y Kohar, 2018); y que las secuencias de tareas que diseñan, no muestran de manera explícita y consciente “el objetivo de enseñar la complejidad de los objetos matemáticos y la articulación coherente de los componentes de esta complejidad” (Robles et al., 2014, p. 70). Para los estudiantes, algunos obstáculos al comprender el TFC, radican en la dificultad de comprender otros objetos matemáticos complejos, tales como función, continuidad, derivada e integral, razón de cambio y acumulación, no relacionar integral definida con área o ver como estáticas las variables, es decir, estos objetos no aparecen claros en sus mentes, lo que conlleva a que se conformen con imágenes que tienen sólo aspectos parciales de la definición o de algún ejemplo particular (Thompson y Dreyfus, 2016; Kouropatov y Dreyfus, 2013; Cordero, 2003; Carlson et al., 2002; Coelho, 1998; Thompson, 1994; Dreyfus, 1990). De hecho, el TFC algunas veces no se percibe como fundamental para los estudiantes de ingeniería (Thompson y Dreyfus, 2016).

Sobre algunos problemas de la forma tradicional de enseñar el TFC, se referencian entre muchos otros, los trabajos con estudiantes de pregrado de Radmehr y Drake (2017), y el de Rosyidi y Kohar (2018) mostrando tanto inconvenientes en la parte algorítmica como en la interpretación del TFC:

Nota: Rosyidi y Kohar (2018).

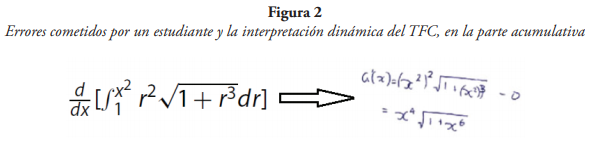
Nota: Radmehr y Drake (2017).

Este panorama constituye la realidad actual en relación con los aspectos de la enseñanza y el aprendizaje del TFC, expuestos por investigadores para ser estudiados, tanto por comunidades de matemáticos, como por aquellas de profesores universitarios. En este contexto no parece estar explícita la necesidad de incorporar a las matemáticas una perspectiva histórica para la búsqueda de estrategias que exploren formas de recuperar argumentos que permitan ver más allá, como es el caso de aquellos empleados por Newton y Leibniz en sus trabajos sobre el TFC. ¿Cómo articular la historia de la matemática y la historia de la educación, para realizar propuestas que respondan a tantas demandas de mejora de la educación matemática y de la enseñanza del cálculo en contextos universitarios?

La incorporación de la historia en la educación matemática universitaria se ha realizado desde diferentes perspectivas. Una de ellas es la que se desarrolla a partir de las huellas que los problemas de enseñanza y aprendizaje del TFC plantean a la comunidad de investigadores. En este sentido, se cuenta con el estudio de caso de la transposición didáctica de la demostración del TFC (Klisinska, 2005). Por otro lado, la investigación de Coelho (1998) indaga sobre la comprensión del vínculo entre derivadas e integrales. Así mismo, en otro estudio se plantea definir de otra manera los diferenciales, y desde allí, tener otra perspectiva del TFC (Biehler et al., 2017; Thompson, 1994).

Desde el marco de la abstracción reflexiva, se cuenta con el análisis de la integral definida (Aranda y Callejo, 2015). También, se dispone de investigaciones alrededor de la parte evaluativa del TFC (Ponce, 2014); y sobre cómo los estudiantes lo aplican a problemas físicos y gráficos (Bajrachrya, 2014). Asimismo, la tesis doctora de Cook (1999) analiza el aprendizaje del TFC y cómo se ve afectado al implementar softwares matemáticos. Se cuenta además con otras investigaciones sobre cómo enseñar el TFC de una manera experiencial, experimental e intuitiva (Rosenthal, 2016), o algunas que describen problemas sobre la enseñanza-aprendizaje del TFC (Cantor Chitiva, 2013; Pettersson y Scheja, 2008; Trouche, 2005; Berry y Nyman, 2003; Hazzan y Leron, 1996; Macduffe, 1947; Hodgson, s.f.). 

Otra perspectiva es la que explora en la historia del TFC, para identificar diferentes teoremas que se denominan como TFC, diferentes demostraciones de un mismo enunciado denominado TFC; o argumentos invariantes en diferentes teoremas o diferentes demostraciones (Mena, 2014; Ponce, 2013; Bressoud, 2011; Lopez, 2011; Katz, 2008; Stoll, 1993), estos aspectos (enunciados, argumentos, patrones, demostraciones, teorías, etc.) se denominan en este trabajo como aspectos históricos del TFC.

Centrar la mirada a la búsqueda de aspectos históricos permite analizar la construcción de un saber partiendo del encuentro con otros saberes, de comprender las uniones con las otras actividades científicas y de reunir diferentes campos de las matemáticas (Barbin, 2006). Además, abordar la perspectiva histórica de procesos, conceptos, teoremas, etc. que se piensan desarrollar, le permite al estudiante comprender que ellas tienen un estatus de actividad cultural inseparable de las otras actividades y prácticas humanas (Barbin, 2006); le ayuda a incrementar la motivación en el aprendizaje; mostrar el lado humano de las matemáticas; mostrar a los estudiantes que no son los únicos con esos inconvenientes procedimentales; ver el lugar de las matemáticas en la sociedad; comparar los procedimientos matemáticos de antes con los actuales para restablecer el valor de las técnicas modernas (Fauvel, 1991).

No obstante, “hay que recordar que uno de los principales aportes de la historia es mostrar que las nociones y conceptos que enseñamos fueron inventadas para resolver problemas (Barbin et al., 2018, p. xxi)”. Es habitual enseñar en un aula de clase un concepto matemático para resolver luego una serie de problemas, mientras que, desde el desarrollo histórico, se evidencia que para resolver un problema (como sucede a menudo en la vida real) se necesita el uso de muchos conceptos (Barbin et al., 2018; Fauvel y Van Maanen, 2002). Luego, este camino que se traza usando argumentos históricos, como uno de los múltiples aspectos históricos que se pueden explorar, puede ser una ruta para cumplir con las tres condiciones frecuentes, que según el IREM (Instituts de recherche sur l’enseignement des mathématiques), deben tener las investigaciones que se abordan desde la historia para que interesen a los profesores: deben ser un estudio diferente (exótico), epistemológico y cultural (Barbin, 2006).

Explorar el TFC desde la perspectiva histórica de los argumentos que fueron desarrollados por quienes resolvían problemas y elaboraban formulaciones, requiere el estudio de Newton, Leibniz, Barrow, Bonaventura Cavalieri, Pierre de Fermat, John Wallis, Isaac Barrow, Hendrick van Heuraet, James Gregory, Leonhard Euler, Joseph-Louis Lagrange, Augustin-Louis Cauchy, entre otros; todos matemáticos que trabajaron con objetos explícitos o implícitos del TFC (Blåsjö, 2015; Mena, 2014; Ponce, 2014; Ponce y Maldonado, 2013; Bressoud, 2011; Guicciardini, 2011; Lopez, 2011; Katz, 2008; Panza, 2000; Stoll, 1993). 

El espacio para el estudio es amplio y muy prometedor. En el estudio que aquí se presenta, se limita la búsqueda a los trabajos de Newton y de Leibniz sobre lo que hoy es conocido como TFC, como un resultado que emergió al resolver un problema (Bressoud, 2011; Guicciardini, 2008; Panza, 2000), haciendo un análisis de contenido de algunas de sus obras para indagar la naturaleza de sus componentes (Fernandez, 2002) y las exigencias para una visibilización a partir del software Geogebra, como ejemplo de mediación y de rescate de argumentos históricos, pero utilizando la notación moderna. Las características de este software matemático serán descritas más adelante.

2. ¿A qué TFC se hace referencia? 

Lo que se conoce hoy como TFC, y que será la versión a la cual se referenciará en este trabajo, se presenta usualmente en textos universitarios de la siguiente manera:

Nota: Stewart, 2015.

Sin embargo, algunos autores apoyan que se cite al TFC enunciado anteriormente, como el Teorema Fundamental de Cálculo Integral (Bressoud, 2011); y como dato relevante, se cuenta con un estudio de cómo algunos profesores llaman TFC sólo a la primera parte del mismo (1) o a (2), la parte evaluativa (Toumasis, 1993).

En la bibliografía consultada también se evidencia que el TFC no es un objeto estático, sino que participa de nuevas configuraciones epistémicas y a medida que ha pasado el tiempo, han ido apareciendo nuevos significados parciales. En el campo de las matemáticas puras, la evolución del trabajo en Análisis Matemático en diferentes espacios (e.g. espacios de Sobolev, espacios de Banach) ha permitido que el TFC se mantenga vigente, con nuevas adaptaciones e incluso con el cambio de notación requerido. Por ejemplo, emerge en la generalización de las integrales de Kurzweil-Henstock en el espacio multidimensional de Banach, su versión del TFC (Federson, 1999); el trabajo realizado sobre la (p,q)-derivadas y (p,q)-integrales motiva ahí un TFC (Sadjang, 2013).

Se evidencia también el trabajo desarrollado al encontrar la versión global del TFC (el teorema de Stokes) sobre variedades diferenciales compactas (Pfeffer, 1987); del paso de las integrales de Kurzweil-Henstock a las integrales de Szabó-Szaz, cuenta con una versión del TFC (Szaz, 1993). Surge también en el cálculo estocástico, sin usar límites, la prueba algebraica del TFC con la fórmula de Ito (Rajeev, 1997) y algunos trabajos donde se modifican la medida, o se debilita alguna condición en las hipótesis del TFC, o se generaliza el mismo (Swartz y Thomson, 2015; Sobczyk y Sanchez, 2008; Cabral, 2000; Macdonald, 1998; Chae, 1995; Ball, 1989; Schipp y Wade, 1989; Price, 1984; Serrin, 1959).

¿Por qué trabajar con las versiones del TFC de las obras de Newton y de Leibniz? Es conocido que con anterioridad Isaac Barrow tenía una versión propia del TFC, (Ponce, 2013; Ponce y Maldonado, 2013; Panza, 2008; Child, 1916) así como también James Gregory tuvo la suya (Katz, 2008). Sin embargo, la combinación de una técnica algorítmica con un significado parcial del TFC fue lo que convirtió al cálculo en una herramienta práctica (Bressoud, 2011). Los aportes de Newton y de Leibniz en el TFC son precisamente esos; no solamente sabían que la derivación e integración eran procesos opuestos, sino que lo definieron de una manera algorítmica correcta. Bien cita Bressoud a D.T Whiteside cuando afirma que:

“It is very tempting, nevertheless, to admit two criteria into a working definition [of calculus] (without excluding others); first, that differentiation and integration be seen as inverse procedures; and, secondly, that both be defined with respect to an adequate algorithmic technique”. (Bressoud, 2011, p. 103)

En adición, se pueden ver las similitudes y diferencias entre la demostración de Leibniz y Barrow en Lopez (2011), por ejemplo, en cuanto a la forma de notar y trabajar con las proporciones del triángulo característico y diferencial.

Por otro lado, en la obra de Newton y de Leibniz se muestra cómo se relacionaron con este teorema, como un resultado que emergió al resolver un problema matemático (Bressoud, 2011; Guicciardini, 2008; Panza, 2000). En efecto, para Newton el TFC emergió cuando el algoritmo inverso que resuelve el problema de las tangentes, resolvió el problema de las áreas, (Panza, 2000). Sin embargo, para Leibniz las cosas fueron diferentes. Su cálculo inició con la idea que la suma y la diferencia son operaciones inversas (Katz, 2008). Como parte de su trabajo, aparece la parte evaluativa del TFC cuando encontró el área bajo una curva construyendo una curva auxiliar, cuya pendiente es proporcional a la altura de la curva original: “He [Leibniz] demonstrates how to construct an auxiliary curve for which the slope (the ratio of the sides of the characteristic triangle) is proportional to the vertical height of the original curve” (Bressoud, 2011). 

Dicho esto, este escrito iría también en concordancia, por ejemplo, con la necesidad de diseñar, en el campo de la ingeniería, artefactos que funcionen en la práctica, cumpliendo con el propósito y especificaciones que lo motivaron (Olaya, 2013), en este caso, resolver un problema.

En este trabajo se explora y proponen las versiones del TFC de Newton en su manuscrito “The October 1666 Tract on Fluxions” (Iliffe, 2011; Guicciardini, 2009; Panza, 2000) como una forma para presentar la primera parte del TFC, y la versión de Leibniz del año 1693 publicado en “Acta Eruditorum” (Mena, 2014; Bressoud, 2011; Katz, 1993; Struik, 1969) que corresponderá a la segunda parte del TFC. Esta exploración ofrece una presentación alternativa del TFC a la enseñanza, que enfatiza la repetición y no la comprensión, es decir, ofrecer una herramienta distinta a las que son meramente algorítmicas u operativas, pues como resaltan varios autores, bajo esos enfoques el estudiante deja de comprender conceptos y métodos propios del cálculo (Robles et al., 2014; Artigue et al., 1995; Tall, 1991), aunado a los inconvenientes expuestos al comienzo de este escrito. Esta nueva presentación del TFC tiene en consideración los puntos de vista geométrico y dinámico, de Leibniz y de Newton, que podrían ser mediados por el uso de herramientas tecnológicas, pudiendo enseñarse de una manera más intuitiva y visual. En resumen, esta forma de presentación enfatizada en lo dinámico y acumulativo que permite apreciar y entender la relaciones expresadas en el TFC (Dougherty et al., 2003).

3. La metodología de análisis de contenido de textos históricos

En el presente estudio se utilizó el análisis de contenido de textos matemáticos históricos de la fuente primaria del TFC de Newton, posible gracias al trabajo de The Newton Project (Iliffe, 2011), y en el caso de Leibniz, a la fuente secundaria del trabajo sobre el TFC en el Acta Eruditorum (Roinila, 2012; Lopez, 2011; Struik, 1969). Análisis de contenido que se hace bajo los puntos de vista de sus aspectos materiales (determinar la naturaleza de sus componentes: en Newton el sentido dinámico del cálculo, en Leibniz el geométrico) y de sus aspectos tecnológicos; entender sus posibles usos y aplicaciones (Fernandez, 2002).

3.1. Newton y el TFC

Newton trabajó con lo que actualmente es conocido como TFC, cuando el algoritmo inverso que resuelve el problema de las tangentes, solucionó el problema de las áreas (Bressoud, 2011; Guicciardini, 2009; Katz, 2008; Panza, 2000). Se abordará la presentación histórica del TFC desde el manuscrito “The October 1666 Tract on Fluxions”. No obstante, Newton ya tenía esta idea, de manera general, desde 1665 (Guicciardini, 2009; Panza, 2000). Posteriormente, esta relación inversa entre el problema de áreas y el problema de las tangentes vuelve a ser expresada en el libro “De Analysi” de 1669 (Guicciardini, 2009, p. 185).

Para comenzar, en el cálculo de Newton, el movimiento de un punto genera una recta y el movimiento de una recta genera una superficie. Para él, las cantidades generadas por un flujo son llamadas fluentes y sus velocidades instantáneas son las fluxiones. En el manuscrito The October 1666 Tract on Fluxions, Newton desarrolló el problema de las fluxiones en la Proposición 7, es decir, utilizó un argumento para mostrar la relación entre los segmentos generados por objetos en movimiento, y las velocidades puntuales de esos movimientos (Panza, 2000). Luego, en la Proposición 8 realizó el problema inverso de las velocidades, la cual, puede ser vista como el símil de la época a nuestras actuales tablas de integrales (Panza, 2000).

La primera parte del TFC asegura que la razón de cambio del área bajo una curva está dada por la ordenada de la curva que la delimita, por tanto, se presentará el Problema 5 de ese manuscrito, donde Newton halla explícitamente la derivada de un área bajo una curva. Se realiza ésta elección, teniendo en cuenta que los procesos algorítmicos, de lo que hoy conocemos como cálculo integral, ya estaban dados en la Proposición 8.

Nota: University of Cambridge library digital.

Este problema podría traducirse en términos modernos como dada un área representada por una ecuación, encuentre la curva que la delimita. Newton utilizó la siguiente gráfica en su solución (figura del problema 5, figura 5). Él observó que el movimiento por el cual (el área de la región) y se incrementa es bc = q. Es decir:

La conclusión inmediata de esta construcción es que la velocidad con las cuales se incrementan el área x está dada por be, mientras que “el movimiento por el que y se incrementa es bc’’ (Iliffe, 2011), es decir, la razón de cambio del área y es bc = q. Pero las cosas no terminan ahí, porque, además y gracias a la Proposición 7 (el algoritmo de las velocidades) Newton ofrece la forma algorítmica para hallar la derivada de estas áreas. Ésta forma es $-\frac{xy}{xx}=q=bc.$.

¿Cómo hacía Newton para hallar esta curva de ordenada q? En la Proposición 7 (que según Panza tiene toda la forma de un teorema) Newton buscaba la relación de las velocidades de dos o más cuerpos, que al moverse generan dos o más rectas que están relacionadas por una ecuación dada (Panza, 2000). Es decir, dada una ecuación que relaciona x y y se buscada la relación de sus velocidades q y p. En la Proposición 8 (el algoritmo inverso de las velocidades) Newton plantea que: dadas las velocidades p/q y una ecuación que relaciona las líneas x y y, se debe encontrar y. Para esto, Newton consideró tres casos en la relación dada y posteriormente agregó algunos ejemplos. Se trata así de un conjunto de procesos puramente algorítmicos que como dice Panza “configuran un dominio real de investigación… que será llamado más adelante Cálculo Integral” (Panza, 2000; p. 507). Utilizando la notación actual, se presenta a continuación el Ejemplo 1 planteado por Newton inmediatamente después del problema 5.

Ejemplo: Suponga que la ecuación y=$\frac{2x}{3}\sqrt{rx}$ describe un área. Ésta ecuación es equivalente a $-4r{x}^3+9y^2=0$. Así, aplicando el algoritmo de derivación de Newton se tiene:

$\mathit{-}\frac{\mathit{x}\mathit{x}}{\mathit{x}\mathit{y}}\mathit{=}\mathit{-}\frac{\mathit{(}\mathit{-}\mathit{12}\mathit{x}{\mathit{r}}^{\mathit{2}}\mathit{)}}{\mathit{18}\mathit{y}}\mathit{=}\frac{\mathit{12}\mathit{r}{\mathit{x}}^{\mathit{2}}}{\mathit{18}\mathit{y}}$. Por lo tanto, $\sqrt{rx}=q$.

Esto es, si se re-escribe el área dada como $y=\left(\frac{2}{3}\right)r^{\frac{1}{2}}{x}^{\frac{3}{2}}$ se tiene que:

$\frac{\mathit{12}\mathit{r}{\mathit{x}}^{\mathit{2}}}{\mathit{18}\mathit{y}}\mathit{=}\sqrt{\mathit{r}\mathit{x}}\mathit{=}\frac{\mathit{d}}{\mathit{d}\mathit{x}}\mathit{\left[}{\mathit{\int }}_{\mathit{a}}^{\mathit{x}}\sqrt{\mathit{r}\mathit{t}}dt\mathit{\right]}$

3.2. Leibniz y el TFC

El cálculo de Leibniz “inició con la idea que la suma y la diferencia son operaciones inversas” (Katz, 2008, p. 572). Para Leibniz, surge lo que se reconoce como la parte evaluativa del TFC, cuando logró hallar el área bajo una curva construyendo una curva auxiliar, cuya pendiente es proporcional a la altura de la curva original (Bressoud, 2011). La versión del TFC que será trabajada a continuación es de 1693 y aparece en “Acta Eruditorum” (Struik, 1969). No obstante, Leibniz venía desarrollando esta idea desde tiempo atrás. En efecto, el primer atisbo de su trabajo en este aspecto está en su escrito “Methodus tangentium invers” de 1673, donde aparecen frases como “regress from the tangents or other functions to the ordinates”, (Scriba, 2014, p. 114). ¿Por qué no presentar en este escrito una versión anterior a la de 1693? Porque el método empleado por Leibniz en ese entonces el era el desarrollo en series de potencias. Por ahora, se elige la entrada geométrica que favorece la visualización, y que puede ser ambientada posteriormente con el uso de Geogebra.

Como dato histórico del uso de la notación, en esta revista “Acta Eruditorum”, Leibniz introdujo por primera vez el símbolo (:) para denotar la división, es decir, $\frac{a}{b}$ = a:b (Boyer, 1959).

La figura 6, que aparece a continuación, contiene la figura 2 del “Acta Eruditorum”, (Roinila, 2012). En esta, los puntos entre paréntesis (H), (F), (C) y (B) son infinitesimales, aunque suene extraño: “Furthermore, there is notation that strikes the eye, used to represent points infinitesimally close to each other; for instance, (F) is infinitesimally close to F, (H) infinitesimally close to H and C to (C)” (Lopez, 2011, p. 2).

La curva AH(H) es la figura a la cual se le pretende hallar su área. La curva C(C) es la curva cuya derivada en C es precisamente FH. Se debe tener en cuenta que Leibniz alcanzó su resultado comparando los triángulos TBC (triángulo característico) y CE(C) (el triángulo diferencial) (Bressoud, 2011; Lopez, 2011). Toda ésta reconstrucción de la demostración geométrica de Leibniz puede verse en la figura 6 que sigue a continuación.

Ahora, utilizando una notación moderna y usando el resultado de Leibniz, se puede concluir la segunda parte del TFC, su parte evaluativa. Es decir:

Si se quiere hallar el área bajo una curva con ordenada y, lo que se necesita es encontrar una curva z tal que z = ∫ ydx . Es decir, si y=f(x), se debe buscar z=F(x) (su antiderivada) que satisfaga:

$\frac{dz}{dx}=\frac{y}{1}\to dz=ydx$

De manera particular, ${\int }_a^{x}dz={\int }_a^{x}ydx$, ao análogamente,

$F\left(x\right)\hspace{0.17em}= {\int }_a^{x}dz={\int }_a^{x}ydx={\int }_a^{x}f\left(x\right)dx.$

En estos términos, F(a)=0, entonces $F\left(x\right) - F\left(a\right) = {\int }_a^{x}f\left(x\right)dx.$ Se acaba de demostrar la siguiente versión del TFC (2), (Lopez, 2011): Teorema: Sea f : [a,b] → R una función continua y suponga que F : [a,b] → R es una antiderivada para f, es decir, F es continua en [a,b], diferenciable en (a,b) y F´ (x) = f (x) para todo x en (a,b). Entonces:

${\int }_b^{a}f\left(x\right)dx=F\left(b\right) - F\left(a\right)$

4. Exploración de herramientas tecnológicas para mejorar la visualización del TFC 

Este trabajo plantea elementos para una articulación entre historia y tecnología en contextos curriculares. Los elementos obtenidos del estudio histórico se exploran con herramientas tecnológicas en la búsqueda de estrategias que aportan recursos a los diseñadores de currículos (y profesores diseñadores de actividades), para la enseñanza del cálculo y en particular del TFC, en respuesta a los escritos que señalan que las reformas del cálculo y el uso de tecnologías parecen no aportar lo suficiente para mejorar la comprensión de los estudiantes, debido a que, en parte, no hay cambios fuertes en el currículo (Thompson et al., 2013). Sin embargo, ¿cómo se podrían emplear las herramientas tecnológicas para actualizar argumentos históricos con un valor didáctico? Se entiende que un argumento histórico tiene un valor didáctico si el mismo es usado como un recurso en actividades de enseñanza o de aprendizaje de las matemáticas. El rol principal de estos softwares es el de la mediación. Ahora, como se tienen estos argumentos históricos, pero con la notación de la época, la mediación está en que se captura el argumento histórico y se utiliza en el software con la notación moderna, es decir, el contenido va cargando ese argumento histórico que tiene una restricción noética en la notación, pero el argumento no tiene dicho condicionamiento.

El otro papel del software matemático es ayudar a la construcción de esas tareas o actividades de enseñanza, en este caso, basados en las versiones del TFC de Newton y de Leibniz. Se plantea así una nueva alternativa de presentar el TFC a formadores universitarios, fortaleciendo la visualización y la acumulación como otra opción a “la enseñanza tradicional y en particular la enseñanza universitaria… [que] tiende a centrarse en una práctica algorítmica y algebraica del cálculo y a evaluar en esencia las competencias adquiridas en este dominio” (Artigue et al., 1995).

4.1 ¿Por qué el software Geogebra?

Geogebra es un software de libre distribución, creado en Austria por Markus Hohenwarter, entre los años 2001 y 2002, como parte de su tesis de maestría en educación matemática y ciencias computacionales de la Universidad de Salzburgo. Este software puede ser utilizado en computadores Windows, Mac OS y Linux, además, cuenta con aplicaciones para teléfonos móviles en Android, iPad y Windows (Majerek, 2014). Algunas de las ventajas de este software son: Geogebra es un programa utilizable en diversas plataformas, está en español, es de acceso libre, cuenta con una rica base de datos y con ejemplos variados y disponibles en internet; además, muestra en paralelo la parte algebraica y geométrica, ayudando a que el estudiante vea la conexión entre ecuaciones y gráficas (Takači et al., 2015; Majerek, 2014; Hohenwarter et al., 2008), sin olvidar que por ser una herramienta de multimedia permite captar la atención de los estudiantes (Bognár et al., 2018).

No obstante, lo más sobresaliente de Geogebra es el hecho que permita hacer ilustraciones dinámicas. En efecto, con su opción deslizador se pueden mostrar gráficas de funciones que no sean estáticas, cómo cambian las variables, cómo se incrementa el área bajo una curva, cómo cambia la recta tangente sobre la curva a medida que varía el punto sobre el eje horizontal, etc. Por consiguiente, Geogebra es una herramienta tecnológica que permite mejorar la visualización en dos o tres dimensiones, sin importar el nivel de escolaridad del estudiante (Takači et al., 2015; Majerek, 2014). Visualización que le permite al estudiante hacer sus propias conclusiones, profundizando su conocimiento teórico (Takači et al., 2015).

4.2 ¿Cómo usar Geogebra en la presentación del TFC?

Los objetos matemáticos involucrados en el TFC no son sencillos (Robles et al., 2014; Bressoud, 2011), luego el uso de Geogebra permitiría visualizar algunos de esos objetos complejos y las posibles relaciones entre ellos. Por mencionar algunos ejemplos, usando este software en particular para este teorema, se tienen los siguientes trabajos: hacer cálculos con la función de área como conector entre la integral definida y la antiderivada (McCullough, 2017; Teper, 2015; Golden, 2011; Hohenwarter et al., 2008); cómo hacer una introducción de la primera parte del TFC calculando la razón de cambio del flujo de una bomba de agua (Schwartz, 2015) o mediante diferenciales (Walker, 2016); y cómo realizar la integral definida de la segunda parte del TFC por aproximaciones de sumas de Riemann (Kumar, 2015), en relación con su antiderivada (Almeida, 2018; Rosenthal, 2016) o usando el teorema del sándwich (Lacoste, 2016).

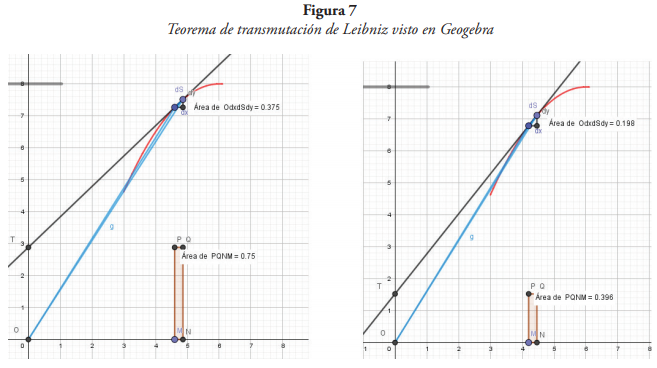
Ahora, bajo las presentaciones históricas mostradas anteriormente, un primer paso podría ser utilizar Geogebra para mostrar el predecesor del TFC de Leibniz, este es, su llamado Teorema de Transmutación (Mena, 2014). En efecto, Leibniz no se concentró exclusivamente en desarrollar sus ejercicios mediante series infinitas (Scriba, 2014), sino como se mostró anteriormente, llegó al TFC empleando el triángulo diferencial y su relación con el triángulo característico, es decir, aplicando métodos geométricos. Este argumento geométrico también fue usado en su Teorema de Transmutación (Katz, 2008). Básicamente, este teorema muestra la relación entre el área de un triángulo diferencial y un rectángulo formado por las prolongaciones de sus lados a los ejes. Por ejemplo, en la figura 7 puede verse la relación dinámica entre el área del triángulo OdSdxdy con el rectángulo PQNM (una es la mitad de la otra), realizada en el software Geogebra.

Como un dato histórico extra de este teorema que precede a su versión del TFC, Leibniz envió en 1676 su teorema de transmutación a Newton, redactando también en esta carta sólo los detalles básicos aritméticos de su cuadratura del círculo, respondiendo así a la carta que sería llamada por Newton epistola prior, donde él también le omitió a Leibniz los métodos de su cálculo. Este hecho fue usado décadas posteriores por Leibniz, como parte de su defensa, de que él nunca recibió ningún dato del cálculo diferencial del genio inglés, y que en lo que a Leibniz concernía, él creía que Newton tenía un método para resolver un problema diferente del suyo (Bardi, 2006).

5. Conclusiones

Leibniz y Newton resolvieron de manera independiente el problema de las áreas y las tangentes, propusieron un resultado y brindaron un algoritmo para su uso. Estos grandes matemáticos diseñaron un método para resolver un problema, mostrando diversidad de soluciones y abriendo así nuevos caminos para las generaciones siguientes de matemáticos, lo que ayudó a la fundamentación de lo que se convertiría, desde el siglo xviii, en el análisis matemático.

La accesibilidad a conceptos matemáticos que son considerados complejos o importantes exclusivamente por su aplicabilidad, inspira a volcar la atención en la educación que recupera la tradición histórica y que la integra a la reflexión didáctica, y que apoyada, por ejemplo, en ideas geométricas, generan una articulación de estructuras provenientes desde diversos campos del saber en las investigaciones que la incorporan, así como sucede a menudo con las áreas de las ciencias básicas:

L’histoire est une ressource pour une approche pluridisciplinaire de l’enseignement des sciences... Nous citerons la théorie de la reproduction de BUFFON pour les liens entre la biologie et la physique, la musique chez Euler pour les liens entre les mathématiques, la physique et la biologie, les atomes au XIXe siècle pour les liens entre la physique et la chimie, les écrits de GALILEE, pour les liens entre les mathématiques, la physique et l’astronomie (Barbin, 2006, p. 5)

El análisis de contenido de textos históricos permite, entre muchas otras cosas, determinar frases, títulos, símbolos, caracteres, comparar temáticas que son importantes para la investigación que la utiliza. Este trabajo se constituye como, precisamente un análisis, cuya principal característica es la aplicación general, como lo denomina Flory Fernandez (2002), es decir, aquella que busca aprovechar la disponibilidad de equipos y software que facilitan su puesta en práctica.

Las herramientas tecnológicas son poderosos recursos actuales para el diseño de tareas, con argumentos históricos y con un alto valor didáctico en procesos instruccionales. Por ejemplo, Geogebra permite visualizar algunos objetos matemáticos complejos y ciertas relaciones entre ellos, de una manera dinámica.

6. Reconocimientos

El autor agradece a la Universidad de La Salle, al proyecto ACACIA (561754-EPP-1-2015-1-COEPPKA2- CBHE-JP) cofinanciado por el programa Erasmus+ ACACIA: Centros de Cooperación para el Fomento, Fortalecimiento y Transferencia de Buenas Prácticas que Apoyan, Cultivan, Adaptan, Comunican, Innovan y Acogen a la comunidad universitaria, y al Doctorado Interinstitucional en Educación de la Universidad Distrital Francisco José de Caldas, en el que se desarrolla el proyecto de investigación de su autoría titulado “Articulación de aspectos del Teorema Fundamental del Cálculo de Newton y de Leibniz en la formación de ingenieros” del cual hacen parte los avances aquí presentados.