Ciencia, Economía y Negocios, Vol. 9, enero-diciembre, 2025 ISSN (Impreso): 2613-876X • ISSN (En línea): 2613-8778
La equivalencia de la Emisión y la Huella de Carbono Per cápita en un modelo de la curva ambientar de la economía mundial: cointegración no lineal e impacto en el calentamiento global
The equivalence of Emissions and Per capita Carbon Footprint in a global economy environmental curve model: nonlinear cointegration and impact on global warming
DOI: https://doi.org/10.22206/ciene.2025.v9.3530
Rolando Reyes1
Recibido: 08/05/2025 • Aprobado: 02/12/2025
Cómo citar: Reyes, R. (2025). La equivalencia de la emisión y la huella de carbono perca pita en un modelo de la curva ambientar de la economía mundial: cointegración no lineal e impacto en el calentamiento global. Ciencia, Economía y Negocios, 9, 95-139. https://doi.org/10.22206/ciene.2025.v9.3530
Resumen
Se formula un modelo de Curva Ambiental (CA) que parte de la equivalencia de las Emisiones Per capitas de Carbono (EPC) y la Huella de Carbono Per cápita (HCP). Dicho modelo contiene las ecuaciones de la relación entre el crecimiento del Ingreso Per cápita (IP) y las EPC para los tres tramos de la CA, las que, por la equivalencia, también son válidas para la relación entre la HCP y el IP. La HCP menos la cantidad de tierra per cápita destinada a la absorción representa el déficit de la huella, el que, multiplicado por la capacidad unitaria de absorción de cada gha, equivale a la cantidad de CO2 per cápita en que aumenta el volumen de este concentrado en la atmosfera, lo que produce el calentamiento global, y que es estimado mediante la ecuación integrada que se construye a partir del modelo. Según la teoría y la ecuación de la equivalencia, la CA de las EPC en función del IP podría tener forma de W invertida, con una segunda etapa de tramo ascendente, lo cual se podría explicar por un aumento del consumo y una disminución del ahorro que financia las inversiones en tecnologías ahorradoras de emisiones, mientras que al mismo tiempo, la CA de la HCP en función del IP podría continuar en un tramo ascendente, debido a una disminución de la cantidad de tierra destinada a la absorción de carbono y de su capacidad biológica. Las estimaciones econométricas de las ecuaciones de las dos CA que se derivan del modelo presentado son coherentes y consistentes con los resultados esperados, encontrándose que tanto la EPC como la HCP tienen una alta y significativa correlación con el IP. Los resultados de las pruebas de raíz unitaria muestran que las series son no estacionarias, con niveles robustos de cointegración y relación de causalidad entre las variables de las ecuaciones de regresión, lo cual es compatible con los resultados esperados según los fundamentos teóricos del modelo formulado.
Palabras clave: Crecimiento sostenible; huella ecológica; curva ambiental; calentamiento global; capital natural; sostenibilidad; desarrollo sostenible; cointegración no lineal.
Codificación JEL: Q54; Q56; O44; C32.
Abstract
A model of the Environmental Curve (EC) is formulated, starting from the equivalence between per capita carbon emissions (PCE) and the per capita carbon footprint (PCF). This model contains the equations describing the relationship between the growth of per capita income (PCI) and PCE across the three segments of the EC, which, by equivalence, are also valid for the relationship between PCF and PCI. The PCF minus the amount of per capita land allocated for carbon absorption represents the footprint deficit, which, when multiplied by the unit absorption capacity of each global hectare (gha), is equivalent to the per capita volume of CO₂ that accumulates in the atmosphere, producing global warming. This warming is estimated through the integrated equation derived from the model. According to the theory and the equation of equivalence, the EC of PCE as a function of PCI could take the form of an inverted W, with a second upward segment. This may be explained by increased consumption and a reduction in savings, which limits investment in low-emission technologies. Meanwhile, the EC of PCF as a function of PCI may continue in an upward trend due to the decline in both the land area allocated for carbon absorption and its biological capacity. The econometric estimates of the two ECs derived from the model are coherent and consistent with theoretical expectations. Both PCE and PCF are found to have a strong and significant correlation with PCI. The results of unit root tests show that the series are non-stationary, with robust levels of cointegration and causality between the regression variables. These findings are consistent with the theoretical foundations of the model formulated.
Keywords: Sustainable growth; ecological footprint; environmental curve; global warming; natural capital; sustainability; sustainable development; nonlinear cointegration.
JEL Codes: Q54; Q56; O44; C32.
Introducción
Los principales componentes de las ciencias de la sostenibilidad abordado en este articulo están vinculados a las teorías del capital natural, huella ecológica y curva ambiental de Kuznets. La Huella ecológica es quizás el más popular y conocido indicador de sostenibilidad fuerte. No es una teoría que surge de la observación del mundo real, sino una construcción numérica que intenta cuantificar la cantidad de tierra requerida para absorber las emisiones que produce el proceso de crecimiento, contrario al caso de la curva ambiental, teoría que surge de la observación de que, en los países de altos ingresos, las emisiones per capitas, o por unidad de ingreso, son menores que en los países de bajos ingresos.
Martin Palmero, F. (2004) analiza el primer modelo de sostenibilidad de Solow de 1974 como punto de partida, derivando a partir de sus ecuaciones fundamentales, las condiciones necesarias para el crecimiento sostenible, las cuales dependen de la elasticidad de sustitución entre el capital físico y el natural, y de la diferencia entre el crecimiento de la productividad del capital natural que produce el progreso técnico, y la tasa a que dicho capital natural se agota. A partir de aquí los estudios e investigaciones se concentraron en los niveles de sostenibilidad del crecimiento y el desarrollo sostenible, en el que la sostenibilidad débil ha planteado y defendido la hipótesis de que la citada elasticidad de sustitución es igual o mayor que la unidad.
A partir del surgimiento de la curva ambiental de Kuznets, gran parte de la atención de los estudios se ha dirigido al intento de incorporar la misma a los modelos de crecimiento, incluyendo principalmente al modelo original de Solow, aunque no ha sucedido lo mismo con el caso de la Huella ecológica, a pesar de que esta también surgió para la misma época. Para incorporar la Huella ecológica a los modelos de crecimiento, de forma tal que la misma sea compatible con la curva ambiental, habría que separar la biocapacidad requerida para la absorción de las emisiones del total de la biocapacidad disponible.
Si la hipótesis de la existencia universal de la curva ambiental de Kuznets es verdadera (tal y como lo sugiere el hecho de que a pesar de que desde 1972 el déficit ecológico per cápita (calculado según la metodología de Huella) ha sido permanente, el crecimiento del ingreso per cápita continua), entonces existe el gran problema de explicar las razones por las cuales las restricciones del capital natural y de la biocapacidad no han paralizado el crecimiento. Aunque los partidarios de la huella ecológica y la sostenibilidad fuerte podrían argumentar que la explicación se encuentra en la acumulación de un pasivo igual a la suma equivalente del déficit de la huella de carbono (que se encuentra depositado en la atmósfera), constituyendo dicho déficit un indicador del exceso de crecimiento.
La Emisión Perca pita de carbono (EPC) es el resultado de dividir las emisiones totales entre la población, mientras que la Huella de Carbono Perca pita (HCP) es la cantidad de tierra per cápita necesaria para absorber dichas emisiones, de donde se desprende que existe una equivalencia entre las dos variables, tal y como lo expresa la siguiente ecuación:
La teoría de la Curva Ambiental (CA) plantea que existe una relación en forma de U invertida entre las EPC y el Ingreso Per cápita (IP), por lo que, dada la equivalencia, dicha relación también debería existir para la HCP. La CA vincula el tramo descendente de la misma al progreso tecnológico que aumenta la productividad y reduce las emisiones, y al aumento de la demanda de calidad ambiental, efecto que produce el crecimiento del IP. Pero según su método de cálculo, la HCP podría disminuir con un aumento de la cantidad o la capacidad de absorción de cada gha, sin que sea necesario un aumento del IP, en cuyo caso se plantearía un problema de causas diferentes para un mismo efecto.
Según el tramo descendente de la CA, el crecimiento del IP mejora la calidad ambiental a través de una reducción de las EPC, mientras que, según la HCP, tal cosa puede ocurrir también mediante un aumento de la capacidad de la tierra para absorber CO2. Pero si el crecimiento del IP mejora la distribución del uso de la tierra y aumenta su capacidad biológica, se registraría la misma relación que en el caso de las EPC, manteniéndose la equivalencia de la ecuación anterior dentro de la misma CA.
El problema anterior se puede abordar apropiadamente mediante un modelo de crecimiento del IP que incorpore la inversión en la optimización del uso de la tierra y en el crecimiento de su capacidad biológica, lo que se lograría incluyendo en el mismo una ecuación que represente la cantidad y la capacidad de la tierra para absorber las EPC que produce dicho crecimiento, con lo cual se estaría unificando la HCP con la teoría de la CA.
En este artículo se analiza la equivalencia de la EPC y la HCP en el marco teórico de la curva ambiental de Kuznets, así como también sus vinculaciones con el crecimiento sostenible y el calentamiento global. Se desarrolla un modelo de curva ambiental en el que ambas variables pueden ser explicadas en función del IP, para lo cual se parte de la condición de equivalencia, incorporando la restricción de la cantidad de tierra, lo cual es consistente con la insuficiencia de dicha cantidad, lo que a su vez genera el déficit de la huella de carbono representativo del exceso de crecimiento.
El crecimiento de las emisiones de residuos sólidos, líquidos y gaseosos de las actividades humanas de producción y consumo, y del ingreso per cápita, se han registrado de manera simultánea, lo que significa que el capital natural, representado por el valor de la biocapacidad terrestre, no ha sido una restricción del crecimiento, mientras que las evidencias empíricas indican que las emisiones per capitas de los países de mayor ingreso per cápita son mayores que las de los de menores ingresos. Un aumento en la productividad del capital natural, una disminución de la tasa de emisión de contaminantes, y del costo del daño que los mismos producen, serían los factores fundamentales para tomar en cuenta.
Tomando en cuenta todo lo anteriormente expuesto, y partiendo del papel que juega el capital natural (cantidad de tierra productiva disponible en el proceso de crecimiento, y de la incidencia de las restricciones del costo social de la contaminación (y del costo de reducirla en el proceso de inversión y de acumulación de capital), este articulo pretende aportar la unificación de la huella de carbono per cápita con las emisiones per capitas en una misma curva ambiental, lo que permitiría explicar, simultáneamente, la existencia conjunta del déficit de la huella y el crecimiento del ingreso, y el crecimiento de la acumulación de gases de efecto invernadero en la atmosfera, causante del calentamiento global.
El articulo incluye cuatro secciones adicionales. En la segunda que sigue a continuación se presenta una revisión de la literatura reciente sobre el tema abordado. La tercera presenta los fundamentos de la nueva teoría de la unificación de la curva ambiental y la huella ecológica en un modelo de crecimiento sostenible. La cuarta presenta la estimación empírica de las ecuaciones del modelo anterior y la cuantificación de los efectos de la emisión y la huella en el calentamiento global, mientras que la quinta y última presenta las conclusiones y sus implicaciones para la agenda de investigación de la relación entre emisiones, huella de carbono y cambio climático.
Revision de la literatura
En Grossman y Krueger (1991) se presenta el articulo seminal sobre la teoría de la curva ambiental. Utilizando medidas comparables de tres contaminantes del aire en una muestra representativa de áreas urbanas ubicadas en 42 países, los autores estudian la relación entre la calidad del aire y el crecimiento económico, encontrando que para dos contaminantes (dióxido de azufre y “humo”) las concentraciones aumentan con el PIB per cápita en niveles bajos de ingreso nacional, pero disminuyen con el crecimiento del PIB en niveles más altos de ingreso, lo cual constituye la primera confirmación empírica de la existencia de la curva ambiental.
En otro estudio posterior (Grossman y Krueger, (1995)), los autores no encuentran evidencias de que la calidad ambiental se deteriore de manera constante con el crecimiento económico. Más bien, para la mayoría de los indicadores, el crecimiento económico trae consigo una fase inicial de deterioro seguida de una fase posterior de mejora. Los puntos de inflexión para los diferentes contaminantes varían, pero en la mayoría de los casos ocurren antes de que un país alcance un ingreso per cápita de $8000, con lo cual los citados autores aportan una segunda evidencia de la existencia de la curva ambiental.
En Wackernagel y Rees (1996) se presenta el articulo seminal de la definición y el concepto de la huella ecológica, cuyo núcleo central es el planteamiento y aplicación de una metodología para medir la carga que una determinada población impone sobre sobre los ecosistemas naturales, los cuales, dada la cantidad fija de tierra, tienen una capacidad limitada para sostener los niveles de consumo y absorber los residuos que generan las actividades de producción y consumo de dicha población.
Una de las evidencias más contundentes del estado del arte de la ciencia de la sostenibilidad es que la versión débil de la misma está presente en la práctica y seguirá estando en las perspectivas de las futuras investigaciones, y de las mismas también se puede inferir que la Sostenibilidad absurdamente fuerte, (la que plantea que el capital natural no solamente no puede ser reemplazado por el capital físico, sino que también plantea que la utilización de los ecosistemas también debe ser eliminada, el cual podría ser el caso de huella de carbono), no tiene espacio y aceptación significativa.
La Sostenibilidad es el objeto del estudio de la “Ciencia de la Sostenibilidad”. Al respecto, Fang et al. (2018) presentan el que quizás sea el estudio más completo del Estado del Arte en este campo científico. Usando el enfoque PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analyses), los autores identificaron un total de 43 publicaciones elegibles para la caracterización o definición del objeto de estudio, y un total de 70 elegibles para la definición de las preguntas de investigación a las que debe responder la Ciencia de la Sostenibilidad.
La interacción entre medio ambiente y sociedad, y su inspiración o vocación hacia el uso, son las dos características que se incluyen en la definición del objeto de estudio de esta nueva ciencia, e identifican un total 16 preguntas de investigación clave que se derivan a partir de la revisión de la literatura realizada según la metodología citada. El aporte más importante de los autores fue la identificación y propuesta de un marco analítico de 8 temas para el análisis de la relación entre las 16 preguntas básicas de investigación identificadas, que es lo que permitiría definir y avanzar en una agenda de investigaciones futuras.
Partiendo de la definición de Sostenibilidad, los retos que la misma plantea, y el conocimiento actual de los sistemas sociales y ambientales (datos, métricas, métodos y teorías), los autores parten de la determinación de las tendencias de largo plazo de los sistemas en un escenario de no intervención. Luego proponen como puntos de agenda de investigación las sinergias y los intercambios entre los sistemas sociales y ambientales, y la adopción de una visión de Sostenibilidad que permita identificar puntos de intervención, que a su vez permitan la transición hacia dicha Sostenibilidad.
Un enfoque de los modelos de crecimiento que incorporan la degradación ambiental ha evolucionado hasta converger en la actualidad a lo que se ha llamado “los modelos de crecimiento verde”, en los que los recursos naturales, renovables y no renovables, y su grado de sustitución con otras formas de capital, entran a jugar un papel de primer orden, tal y como lo plantea Schiliro (2019).
Hay que señalar que quizás una de las principales fuentes de inspiración de los modelos de crecimiento verde sea la crítica hecha por esa misma época a “los límites del crecimiento” que no reconocen los modelos anteriormente citados. La verificación de la huella ecológica del exceso de crecimiento se constituyó en una fuerte aceleración a la velocidad con que se produjeron y se producen investigaciones sobre el crecimiento verde, sin que esto se haya constituido en un obstáculo en el avance de las investigaciones basadas en modelos de crecimiento neoclásicos, con enfoques precisos en cuanto a la incorporación de los recursos naturales al proceso de crecimiento económico (Correa, 2015).
Asimismo, ha surgido otra nueva línea de investigación, que parte del modelo de crecimiento más conocido, y al cual se incorporan las emisiones contaminantes que dicho crecimiento produce, para lo cual se incorpora la Curva Ambiental de Kuznets, generando una nueva versión del modelo de Solow: “The Green Solow Model”. Una excelente exposición del surgimiento, evolución y características del modelo verde de Solow puede encontrarse en Guillo y Magalhaes (2018).
Después de establecer que la revisión de la literatura sobre los vínculos entre el crecimiento sostenible y la sostenibilidad de largo plazo en el marco de los recursos naturales no renovables muestra que dicho crecimiento es posible si se cumplen ciertas condiciones de crecimiento de la población, progreso tecnológico y uso productivo de los recursos naturales, Guillo y Magalhaes (2018, op. cit.) concluyen “que el crecimiento con recursos no renovables y una calidad del aire no deteriorada pueden mantenerse a largo plazo si el progreso tecnológico en la reducción de emisiones es lo suficientemente rápido”. Además, muestran que algunos datos sobre las emisiones de contaminación están bien de acuerdo con las predicciones teóricas de una extensión muy simple del modelo de Solow de un sector (apodado el modelo “Green Solow”)”.
Las críticas más robustas al modelo Green Solow se orientan a resaltar la excesiva orientación al intercambio entre crecimiento y emisiones, que no toma en cuenta la eficiencia en el uso de los recursos, y a la fijaón de manera exógena de un progreso tecnológico ahorrador de emisiones. Con relación a las críticas citadas, Sahu y Shatrunjay (2017), plantean que “existen ciertas limitaciones con el Modelo Green Solow en el contexto de una perspectiva de un país en desarrollo. Por un lado, no ilustra claramente el papel de la tecnología en el proceso de producción, y tampoco muestra su efecto en las emisiones agregadas de un país. Del mismo modo, no muestra los impactos de bienestar de la adición de regulaciones para controlar el flujo de emisiones”
La ausencia de la eficiencia en el uso de los recursos y la reabsorción de desechos de los procesos de producción y consumo (objeto de estudio de la Economía Circular basada en el Reciclaje) es quizás una de las más poderosas críticas a los modelos de crecimiento verde. El impacto de la tasa de reciclaje en el crecimiento verde o sostenible es demostrado en Lenuta, et al. (2019). Después de citar varios estudios que analizan la relación entre el reciclaje, las políticas ambientales y el crecimiento del ingreso, los autores formulan tres hipótesis fundamentales: 1) El crecimiento económico está influenciado positivamente por el número de empleados en las actividades de protección del medio ambiente. 2) La actividad de reciclaje tiene un impacto positivo en el crecimiento económico. 3) La innovación con beneficio ambiental tiene un impacto positivo en el crecimiento económico.
Es muy importante resaltar que el planteamiento de los estudios disponibles y el estado del arte del conocimiento científico sobre la relación entre medio ambiente y crecimiento económico todavía no es concluyente. Un resultado robusto al respecto puede encontrarse en Tiba y Omri (2017). Después de analizar la dirección de causalidad entre (i) las variables de uso de energía (electricidad, nuclear, renovables y no renovables) y el crecimiento de la producción; (ii) entre el crecimiento económico y el medio ambiente; y entre las tres variables al mismo tiempo, los autores concluyen que a nivel mundial, el estado del arte proporciona resultados paradójicos y no concluyentes sobre el asunto de que el consumo de energía pueda impulsar el crecimiento económico a través de la mejora de la productividad, y que al mismo tiempo puede impulsar los daños ambientales a través del aumento de las emisiones contaminantes. Puede considerarse que su estudio es un intento exitoso de arrojar más luz de la relación existente sobre energía, medio ambiente y crecimiento, al ofrecer una lista extensa (1978-2014) de estos vínculos.
Yandle et al. (2004), revisan a profundidad las bases teóricas de la curva ambiental, analizando los fundamentos del planteamiento teórico de que el medio ambiente es un bien superior o de lujo, lo que sería una pieza clave para explicar el segmento descendente de la curva ambiental. Los autores consideran otros posibles factores explicativos, como los derechos de propiedad y la regulación ambiental, los cuales también podrían aparecer y perfeccionarse con el crecimiento permanente del ingreso per cápita.
En Kaika y Zervas (2013) se puede encontrar un artículo que presenta las bases teóricas de la curva ambiental y revisa los factores que explican su aparición, como la transición estructural de la economía, la regulación ambiental, y la conciencia pública. Stern (2015) presenta una revisión histórica de los primeros 25 años de la aparición de la curva ambiental de Kuznets, revisando tanto los fundamentos teóricos que avalan su existencia, así como las evidencias empíricas presentadas hasta esa fecha, críticas teóricas y aportes de modelos de panel y variables omitidas en estudios previos.
La emisión de CO2 es el principal componente de la huella ecológica, pero no es el único, aunque la gran mayoría de los artículos sobre la curva de Kuznets ambiental utiliza las emisiones de CO2 como indicador de la degradación ambiental. El anterior planteamiento es la justificación de Destek et al. (2018) para utilizar la misma huella ecológica y no las emisiones de CO2 como indicador de degradación ambiental. En su estudio encuentran que existe una relación en forma de U entre el ingreso real y la huella ecológica, y que la energía no renovable aumenta la degradación ambiental, mientras que la energía renovable y la apertura comercial la disminuyen en los países de la UE.
Este resultado constituye un punto fundamental para el objetivo unificar la curva ambiental y la huella ecológica en un modelo de crecimiento sostenible del ingreso. Si la relación entre la huella ecológica y el ingreso es de U normal (no invertida como plantea la curva ambiental), entonces la huella ecológica disminuye cuando el ingreso es bajo, pero aumenta cuando el ingreso es alto.
Konya (2022) examina la existencia de la relación entre las emisiones, la huella de carbono y el ingreso, para lo cual analiza datos de panel para someter a prueba la hipótesis de un vínculo en forma de U invertida entre las emisiones de dióxido de carbono, la huella ecológica y el PIB per cápita, encontrando un efecto positivo y significativo del consumo de electricidad sobre la emisión de dióxido de carbono a largo plazo en una ecuación donde la huella ecológica es la variable dependiente. Encuentra una relación en forma de U invertida. Es decir, se encuentran resultados que confirman la existencia de la curva ambiental de Kuznets cuando se utilizan las emisiones en vez de la huella. Enfatiza el hecho de que se observan vínculos causales bidireccionales entre las emisiones de carbono y el crecimiento económico, entre las emisiones de dióxido de carbono y el cuadrado del crecimiento económico, y entre las emisiones de dióxido de carbono y el consumo de electricidad; entre la huella ecológica y el crecimiento económico, entre la huella ecológica y el cuadrado del crecimiento económico, y entre la huella ecológica y el consumo de electricidad.
La forma de la curva y el grado de la ecuación que la representa es un asunto fundamental en todos los estudios empíricos que tratan de probar la existencia de la curva ambiental. En términos matemático, la ecuación que representa la esencia de la teoría de la curva ambiental debería ser de segundo grado, representando una parábola que abre hacia abajo. Sarkodi y Strezov (2019) evalúan la validez general de la curva ambiental para diferentes contaminantes y contextos económicos, para lo cual combinan el meta-análisis y el análisis bibliométrico, encontrando resultados mixtos, y resaltando la importancia de la especificación no lineal para el análisis de la relación entre crecimiento y calidad ambiental.
Pata y Balsalobre-Lorente (2022) exploran la influencia del turismo y el consumo energético en la capacidad ecológica de carga de Turquía mediante un modelo ARDL dinámico, revelando una relación no lineal entre crecimiento y presión ambiental. Utilizando también modelos ARDL no lineales, Ghosh y Shahbaz (2021) analizan la relación entre ingreso, huella ecológica y emisiones de CO₂. Se valida la existencia de la curva ambiental para varios casos, pero con efectos asimétricos que dependen del nivel de ingreso y del tipo de impacto ambiental considerado. Por último, Zhang et al. (2022) demuestran que la EKC existe para las emisiones de CO₂ en los países del G20, pero con puntos de inflexión variables.
Con respecto a la forma de la curva, Lazăr et al. (2019), encuentran que, agregando los resultados de once países de la Unión Europea (CEE), existe un vínculo no lineal creciente entre el PIB y el CO2 para el grupo de países de CEE, aunque los resultados por país revelan que el vínculo entre el PIB y el CO2 se caracteriza por una gran diversidad entre los países de CEE, a saber: en forma de N, N invertida, en forma de U, U invertida, monótona o sin vínculo estadístico. Concluyen que, a pesar de una tendencia ascendente agregada, algunos países de CEE lograron asegurar un PIB más alto con menores emisiones de CO2.
Las evidencias de que la curva que representa la relación entre el crecimiento y la calidad ambiental (independientemente del tipo indicador que se utilice para medirla) es no lineal, y con más de un punto de inflexión, indican que las especificaciones de los modelos econométricos a ser utilizados en el análisis deberían fundamentarse en polinomios de grado mayor a dos.
La cantidad de estudios que utilizan las emisiones de CO2 como indicador de degradación ambiental es mayoritariamente aplastante con relación a los que utilizan la huella ecológica total o la huella de carbono. Pero, aunque la huella es un cálculo basado en una propuesta metodológica, la misma se utiliza en estudios que la vinculan a los efectos del crecimiento económico.
Al respecto, Usman y Makhdum (2021), investigan el nexo dinámico entre la huella ecológica, el valor agregado agrícola, el área forestal, el uso de energía renovable y no renovable y el desarrollo financiero en los países BRICS-T (Brasil, Rusia, India, China, Sudáfrica y Turquía) de 1990 a 2018. Concluyen en que un aumento del 1% en el uso de la energía no renovable y desarrollo financiero produce un aumento de la huella ecológica de 0,5507% y 0,0404%, respectivamente, y que una reducción del 0,7483% y el 0,2248% en la huella ecológica se debe a un aumento del 1% en la silvicultura y el uso de energía renovable, respectivamente. Aunque la rigurosidad econométrica de este estudio no se pueda cuestionar, es necesario resaltar una vez más que la huella no es una variable observable, sino que se calcula a partir de una metodología previamente definida.
Uno de los estudios más recientes en el que se analiza la relación entre la huella de carbono y el crecimiento económico bajo el marco de la curva ambiental puede encontrarse en Wang et al. (2023). Utilizando modelos de panel, encuentran que la curva ambiental se sostiene empíricamente en varios países, pero requiere políticas diferenciadas según la etapa de desarrollo.
Si la teoría de la curva ambiental se acepta como buena y valida, y si los factores de absorción de los ecosistemas y la tecnología permanecen constantes, entonces existiría un vínculo directo entre la citada curva y el calentamiento global: en el tramo ascendente de la curva la concentración de CO2 en la atmosfera estaría aumentando, y por ende, también el calentamiento global, mientras que se esperaría que en el tramo descendente por lo menos disminuya la tasa de crecimiento de dicha concentración, y que la misma sea compatible con la primera y segunda trayectoria socioeconómica compartida (SSP1 y SSP2) del IPCC. Ali y Adebayo (2024) evalúan las trayectorias de los escenarios socioeconómicos compartidos del IPCC integrando el enfoque de la curva ambiental (EKC), concluyendo que el crecimiento sostenible puede lograrse con políticas activas de descarbonización y transformación estructural.
La unificación de la teoría de la curva ambiental y de la metodología de la huella ecológica en un modelo de crecimiento sostenible
Formulación del Modelo
Si existe una tasa de crecimiento sostenible, la ecuación de esta debe incorporar el uso del capital natural en la producción de materiales y bienes finales, y también en la absorción de las emisiones de contaminantes que dicho crecimiento produce, y si se toman en cuenta ambos usos mutuamente excluyentes, entonces se estaría incorporando la restricción de la Huella ecológica, pues un aumento en la cantidad de tierra destinada al primer uso significa una disminución en la cantidad disponible para el segundo uso. Pero la existencia de tal ecuación debería ser compatible con las evidencias que también existe la denominada Curva Ambiental de Kuznets (CAK, o EKC por sus siglas en ingles), lo cual significa que las emisiones de contaminantes deberían ser creciente a una baja tasa de crecimiento del ingreso, y decreciente a medida que aumenta este crecimiento, lo que a su vez significa que debería existir una segunda ecuación que refleje esta relación. Un modelo en el que ambas ecuaciones existan simultáneamente unificaría ambos planteamientos.
El modelo parte de las siguientes ecuaciones:
La ecuación 1 es una función de producción tipo Cobb-Douglas, en la que L es la fuerza laboral, KF es el capital físico, KNp es el capital natural utilizado para la producción de bienes finales y materiales. En términos de medición del capital natural, KNp es equivalente a la tierra de cultivo, según las mediciones de la metodología de la huella ecológica. El valor de µ representa la fracción del capital natural destinado a la producción de bienes finales y materiales. El ultimo componente representa el estado del progreso tecnológico en lo relacionado a la productividad del capital físico y natural utilizado en la producción de bienes y en la adaptación a los efectos del calentamiento global, el cual crece a una tasa constante igual a λ.
La ecuación 2 expresa el ingreso como la suma del consumo y la inversión, destinándose esta en su totalidad a la acumulación de capital físico. La ecuación 3 representa la cantidad de las Emisiones Netas de Contaminantes, ENC, en la que a, b y c representan los factores de emisión del consumo per cápita, el capital físico, y el capital natural utilizado en la producción, respectivamente, mientras que d representa el factor de absorción del capital natural utilizado en la producción de servicios y sumidero de contaminantes. θ representa la tasa del progreso tecnológico determinante de la velocidad a la cual se reducen las emisiones de contaminantes por unidad de producción y consumo (mitigación) y con efectos marginales de adaptación al calentamiento global que produce la acumulación de emisiones en la atmosfera.
Obsérvese que en la ecuación 3 se supone que L, KF y KNp se combinan y participan en el proceso de emisión de contaminantes de la misma forma en que lo hacen en el proceso de producción, lo cual es consistente con el hecho de que las tres variables son fuentes de emisiones contaminantes, y con el hecho de que estas crecen con el crecimiento del ingreso. Aunque θ puede estar correlacionado con los parámetros a, b y c, también puede variar de forma independiente, como en el caso del progreso tecnológico en el campo de las energías renovables.
La ecuación 4 representa la tasa de ahorro, mientras que la ecuación 5 representa el ritmo al cual puede crecer el capital físico per cápita, en la que Φ representa la tasa de depreciación de este, y n la tasa de crecimiento de la población. Obsérvese que la ecuación 5 es una nueva versión de la ecuación básica del modelo de crecimiento de Solow, en la que además de la depreciación y la tasa de crecimiento de la población, se impone la condición de que el ahorro también debe ser suficiente para financiar las inversiones en aumento de la productividad del capital, y en reducción de las emisiones de contaminantes y adaptación al calentamiento global, las cuales, medidas en términos monetarios, representan una proporción del ingreso per cápita igual a sus respectivas tasas de crecimiento.
Por último, la ecuación 6 representa la restricción fundamental de la Huella ecológica, según la cual la cantidad de tierra (capital natural o biocapacidad) esta fija, lo cual significa que la suma de las tasas de crecimiento de sus usos alternativos (producción de bienes o de servicios ecosistémicos), es igual a cero.
Las etapas del crecimiento sostenible del ingreso
De aquí en adelante se supondrá que tanto el crecimiento del ingreso como de las emisiones son procesos que pasan por varias etapas en cuanto a los factores determinantes del mismo. En la primera etapa del crecimiento del ingreso no hay progreso tecnológico, por lo que el ultimo término del lado de derecho de la ecuación 1 no se debe tomar en cuenta. Hecha esta corrección, dividiendo entre L para obtener el ingreso per cápita, y derivando su resultado, se obtiene la tasa de crecimiento del producto per cápita correspondiente a dicha etapa:
En donde g representa la tasa de crecimiento de cada componente de la ecuación y n la tasa de crecimiento de la población. La ecuación 7 tiene muchas interpretaciones e implicaciones que serán analizadas más adelante, pero aquí es necesario destacar que la tasa de crecimiento del ingreso es mayor mientras mayor sea la tasa de crecimiento del uso del capital natural en la producción de materiales y bienes finales.
Sustituyendo 4, la ecuación anterior se transforma en:
En la que .
En la segunda etapa entra en acción la restricción de la huella ecológica (ecuación 6), y aparece el progreso tecnológico que aumenta la productividad del trabajo y de las dos formas del capital, agregando el último término del lado derecho de la ecuación 1, a partir de la cual la tasa de crecimiento sostenible del ingreso per cápita en la segunda etapa (gysse) de la misma se puede expresar de la siguiente manera:
En la segunda etapa se supone también que se cumplen condiciones fundamentales de la Sostenibilidad débil, por lo que el progreso tecnológico que aumenta la productividad total de los factores, puede más que compensar la disminución de tierra o capital natural destinado a la producción de materiales y bienes finales. Por tanto, en la ecuación anterior se cumple que λ1 > µ(1 − α − β)gkns, lo cual significa que la tasa de crecimiento de la segunda etapa siempre será mayor que el de la primera.
En la tercera y última etapa, el progreso tecnológico que incrementa la productividad de los factores se acelera, y la ecuación 9 pasa a tomar la siguiente forma:
En la ecuación 10 se supone que λ2 > λ1, razón por la cual la tasa de crecimiento sostenible del ingreso per cápita de la tercera etapa (gyste) será mayor que el de la segunda etapa.
La conclusión de todo lo expuesto en los párrafos anteriores sobre la teoría de la unificación del crecimiento sostenible con la huella ecológica es que, en presencia de progreso tecnológico acelerador de la productividad total de los factores y amortiguador de los efectos del calentamiento en la reducción del ingreso, la cantidad de tierra o capital natural fijo podría no ser una restricción al crecimiento. Pero el crecimiento permanente del ingreso podría estar generando una tasa de emisión de contaminantes mayor que la que el capital natural destinado a los servicios ecosistémicos podría absorber, cuya acumulación podría provocar una deuda ecológica, lo que sí es compatible con la metodología y el enfoque de la Huella.
Las etapas del crecimiento de las emisiones de contaminantes
En la primera etapa del proceso de crecimiento la economía destina muy poco capital natural a la absorción de contaminantes y a la producción de otros servicios ecosistémico. Tampoco se realizan inversiones en tecnologías que producen mitigación de las emisiones y adaptación al calentamiento global, por lo que la ecuación 3 queda de la siguiente forma:
Dividiendo entre la población, y derivando la ecuación anterior, se obtiene la tasa de crecimiento per cápita de las emisiones netas de contaminantes en la situación de la primera etapa del crecimiento:
La tasa de emisión de contaminantes aumentará con el aumento de la población, el aumento del capital físico, y del capital natural usado en la producción de materiales y bienes finales. En esta primera etapa, el crecimiento del ingreso se produce según la ecuación 7. En una segunda etapa empieza a aumentar la cantidad de capital natural utilizado en la producción de servicios ecosistémicos, por lo que la ecuación de emisión de contaminantes es ahora:
y su tasa de crecimiento per cápita seria:
En esta etapa entra en acción la restricción de la Huella ecológica, la cual debe ser incorporada a la ecuación anterior. Por tanto, la ecuación 14, medida en términos per cápita, se transforma en:
La teoría de la unificación del crecimiento sostenible y la huella ecológica con la curva ambiental plantea que la tasa de crecimiento de las emisiones de la primera etapa crece según las condiciones de la ecuación 12, llegando a un máximo, que luego se estabiliza según las condiciones de la ecuación 15 de la segunda etapa, en el que ambas ecuaciones se igualan, y en el que las emisiones del capital natural usado en la producción son iguales al utilizado en la absorción de emisiones:
Las condiciones en que se cumple la ecuación 16 es el Estado Estacionario del uso optimo del capital natural (Reyes, 2019). En la tercera y última etapa del crecimiento se agrega el progreso tecnológico ahorrador de emisiones y reductor de los efectos del calentamiento global. Las respectivas ecuaciones serian:
Tasas de crecimiento de los ingresos y los costos de las emisiones de contaminantes en los estados estacionarios de la Curva Ambiental
Lo presentado en la sección anterior unifica la teoría del crecimiento sostenible con el enfoque que sustenta la metodología del cálculo de la Huella ecológica, lo que se logra cuando se incorpora al Modelo la restricción fundamental de que la cantidad de capital natural es fija. La demostración de que la curva ambiental es también compatible con la teoría de la unificación debe partir de que la misma plantea que en una primera etapa la tasa de crecimiento del ingreso y de las emisiones son crecientes, que luego las mismas es estabilizan, y que, en una tercera y última etapa, la relación entre las mismas es decreciente.
Emitir contaminantes produce un daño ambiental que tiene un costo. Pero las emisiones se pueden reducir mediante inversiones en tecnologías ahorradoras de estas, los cual tiene otro costo. La teoría (Stern, 2006) plantea que mientras el costo del daño de emitir sea menor que el costo de reducir, las emisiones continuaran, y viceversa, planteamiento fundamental para demostrar que la CAK es compatible con la unificación de la teoría del Crecimiento sostenible y la Huella ecológica. Aunque la ecuación 3 representa la cantidad física de las emisiones de contaminantes, la misma también puede ser interpretada como el costo de dichas emisiones, para lo cual es necesario asumir que el costo del daño de cada unidad de emisión de las actividades de consumo y producción es igual a una unidad monetaria.
Las ecuaciones del crecimiento de las emisiones de contaminantes son simultaneas a las del crecimiento del ingreso, y cuando se analiza simultáneamente las ecuaciones 7 y 12, se concluye que tanto el ingreso como las emisiones de contaminantes crecen con el crecimiento de la población, el capital físico y el capital natural usado para producir, lo que significa que, en la primera etapa del proceso de crecimiento, la relación entre las tasas de crecimiento del ingreso y la emisión es positiva.
En la primera etapa se supone que se inicia un proceso de optimización del uso del capital natural, el cual termina al final de esta, y en el cual su uso en la producción de materiales y bienes finales se reduce, mientras aumenta su uso en la absorción de emisiones y de otros servicios ecosistémicos. Dicho proceso culmina cuando la tasa de crecimiento de las emisiones de contaminantes se hace igual a cero (equivalente a un uso optimo del capital natural, Reyes (2019), y en ese punto la CAK cambia de pendiente, iniciándose su segmento plano, o cuasi plano, correspondiente a la segunda etapa.
Pero en este punto también se inicia la inversión en tecnología que incrementa la productividad de los factores, por lo que en la segunda etapa la ecuación 5 se convierte en:
La inversión en tecnología aceleradora del crecimiento de la productividad aumenta el crecimiento del ingreso, pero además reduce la tasa de emisión de contaminantes al reducir la tasa de crecimiento del capital físico, una de las fuentes de dichas emisiones. Cuando la ecuación 19 es sustituida en las ecuaciones 9 y 15, las mismas toman las formas de los dos componentes fundamentales de una curva ambiental que incorpora la restricción de la huella ecológica:
La teoría de la unificación de la HCP y las ECP en una sola curva ambiental postula la hipótesis de la existencia de dos Estados Estacionarios, el primero de los cuales se produciría en la segunda etapa del proceso de crecimiento, en la que la tasa de crecimiento de las emisiones netas de contaminantes se hace igual a cero (segmento plano de la CAK), lo que significa que la ecuación 21 se transforma en
Según la ecuación anterior, en el primer Estado Estacionario de la segunda etapa, la suma de la tasa de crecimiento de las emisiones del consumo de la población y del capital físico es igual a la tasa de crecimiento de la absorción del capital natural, el cual también se distribuye de manera óptima entre sus dos usos mutuamente excluyentes, y en el que también la tasa de crecimiento de la productividad es mayor que la tasa de disminución del capital natural usado en la producción de materiales y bienes finales.
En la tercera etapa surge la tecnología ahorradora de emisiones, y la ecuación 15 se convierte en:
En el segundo Estado Estacionario de la tercera etapa , lo que significa que gkf = 0, lo que a su vez significa que las ecuaciones 10 y 23 pasan a tener las siguientes formas:
Según la ecuación 24, el crecimiento del ingreso per cápita continúa debido al efecto de la aceleración del crecimiento de la productividad y adaptación al calentamiento global, y en la que λ2 > λ1 + βgkf. Adicionalmente, según la ecuación 19, el ahorro per cápita seria
Lo cual significa que, en el segundo Estado Estacionario, el ahorro financia las inversiones necesarias para mantener el crecimiento de la productividad del capital acumulado, producir adaptación al calentamiento global, y para disminuir el crecimiento per cápita de las emisiones de contaminantes que generan las actividades de la producción y el consumo, lo que significa que la ecuación 25 siempre arrojaría resultados negativos, pues también siempre se cumpliría que:
El cumplimiento de las condiciones de la ecuación 27 garantiza el tramo descendente de la CAK de la tercera etapa del proceso de crecimiento, y con lo cual, se estaría logrando la unificación de las teorías del Crecimiento Sostenible, la Huella ecológica y la Curva Ambiental.
Las etapas del proceso de crecimiento sostenible de la teoría de la Unificación se pueden explicar también geométricamente, lo cual se inicia con el Gráfico 1 que se presenta más abajo.
Gráfico 1
Primera etapa o generación del tramo ascendente de la curva ambiental

La figura de arriba y a la izquierda representa la relación positiva entre el crecimiento del ingreso per cápita y el crecimiento del capital natural usado en la producción y el capital físico per cápita. El proceso se inicia en el punto “a”, en el cual hay una subutilización del capital natural. A partir de dicho punto empieza a aumentar la cantidad de capital físico y la fracción (µ) del capital natural utilizado para la producción de materiales y bienes finales, y también la cantidad usada en la absorción de emisiones contaminantes.
La de abajo y a la izquierda refleja este proceso, en el que la curva de pendiente positiva representa el crecimiento de las emisiones que produce el aumento del capital físico y el natural usado en la producción, mientras que la de pendiente negativa refleja la absorción del capital natural usado en la producción de servicios ecosistémicos. El proceso de la primera etapa culmina en el punto “b”, en el que la tasa de crecimiento de las emisiones es igual a la tasa de crecimiento de las absorciones, y en el que también las emisiones per capitas y el ingreso per cápita son mayores que en el punto “a”, lo cual determina el tramo ascendente de la CAK, según queda reflejado en la figura de abajo y a la derecha.
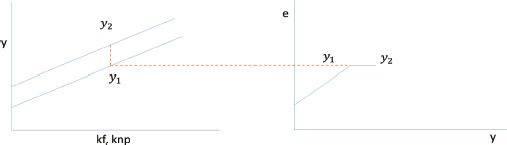
En la segunda etapa aparece el progreso tecnológico acelerador de la productividad del capital físico y del capital natural usado con fines productivos, lo cual produce un desplazamiento hacia arriba y a la derecha de la curva del crecimiento del ingreso per cápita, tal y como puede observarse en el lado derecho del Gráfico 2. El crecimiento del ingreso per cápita se produce sin que se registre un incremento en las emisiones per-capitas, pasando el mismo de y1 a y2, y determinando el segmento plano de la CAK.
Gráfico 2
Segunda etapa o generación del tramo plano de la curva ambiental
En la tercera y última etapa aparece el progreso tecnológico ahorrador de emisiones. En este punto es necesario reiterar que la ecuación 3 presenta tanto las cantidades como los costos de las emisiones, tanto de aumentarlas como de disminuirlas. En la primera etapa los costos de aumentar las emisiones son menores que los costos de disminuirlas, pues el costo de la inversión en progreso tecnológico es muy alto con relación al costo del daño ambiental causado por estas, mientras que en la tercera etapa sucede lo contrario.
El lado izquierdo del Gráfico 3 representan lo planteado anteriormente. El costo marginal de una unidad de emisión disminuye con la cantidad, pues el progreso tecnológico ahorrador de emisiones contaminantes determina que cada vez cueste menos disminuir el costo del daño de la contaminación. El costo marginal de una unidad de reducción también disminuye con la cantidad, pero a una velocidad mayor, pues el progreso tecnológico hace que cada vez cueste menos sustituir procesos de altas emisiones por otros menos contaminantes, como en el caso de la transición energética hacia fuentes renovables, lo que hace que la cantidad de emisiones se reduzca desde el punto 2 al punto 1 en la figura de la derecha.
Gráfico 3
Tercera etapa o generación del plano descendente de la curva ambiental
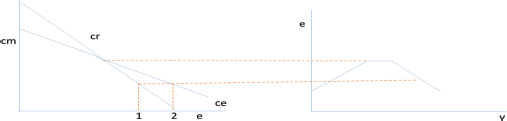
Por último, el segmento de pendiente descendente de la CAK de la figura de la izquierda corresponde a los puntos en los que el costo marginal de reducir es menor al costo marginal de emitir, mientras se mantiene el efecto acelerador de la productividad del progreso tecnológico iniciado en la segunda etapa.
El ahorro y el consumo en el último estado estacionario del crecimiento sostenible.
Las ecuaciones 4 y 5 son válidas solo en la primera y en la segunda etapa del proceso de crecimiento, en la que . En la tercera etapa, en la que , las ecuaciones 4 y 5 se convierten en:
Las ecuaciones anteriores están expresadas en valores totales, y no en términos per cápita, como ha sido del caso las presentadas en secciones anteriores. El interés de la propuesta teórica de la Unificación es ahora el determinar si la economía converge hacia el Estado Estacionario de la tercera etapa del proceso de crecimiento, y en caso de que así sea, como se determinan los valores del ahorro y el consumo de este, y que influencia tienen el progreso tecnológico que aumenta la productividad, y el que disminuye la tasa de crecimiento de las emisiones de contaminantes.
La ecuación 28 muestra claramente que para que aumenten las inversiones en las tecnologías que aumentan la tasa de crecimiento de la productividad y reducen la de las emisiones de contaminantes, es necesario que aumente el ahorro, mientras que la ecuación 29 indica que para que esto suceda, es necesario que disminuya el consumo. La relación entre estas variables queda ilustrada en el Gráfico 4 que se presenta más abajo.
Gráfico 4
El Consumo y el Ahorro en el Estado Estacionario final de la Unificación
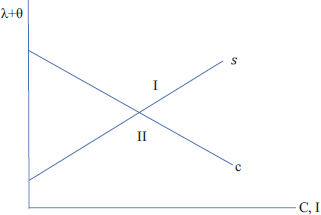
Obsérvese que en el Gráfico 4 el eje vertical representa la suma de λ y θ, lo cual significa la unificación de la tasa del progreso tecnológico que aumenta la productividad, produce adaptación al calentamiento global, y reduce las emisiones, mientras que el eje horizontal representa los valores del ahorro y el consumo. En el punto de intersección de ambas curvas el ahorro y el consumo se igualan, alcanzando los valores del equilibrio del Estado Estacionario de la tercera etapa del proceso de crecimiento, y en el que el ahorro financia las inversiones necesarias para mantener el progreso tecnológico. Si el ahorro sube por encima de ese nivel, y la economía se coloca en cualquier punto de la zona I, y si la inversión en progreso tecnológico no crece a un ritmo mayor que el que financia el ahorro del Estado Estacionario, se generaría un proceso de reducción del ahorro y aumento del consumo, lo que produciría un retorno hacia el punto de intersección.
Si el ahorro se coloca por debajo del nivel de equilibrio del Estado Estacionario, la economía se coloca en cualquier punto de la zona II, colocando el consumo por encima del nivel de equilibrio del Estado Estacionario, en el que existirían oportunidades de inversión en tecnología altamente rentable que demandarían un mayor ahorro para financiarlas, situación que generaría un proceso de aumento del ahorro y reducción del consumo, lo que produciría un retorno hacia el punto de intersección.
Lo anterior conduce a la conclusión de que la economía converge hacia un Estado Estacionario final, en el que se produce un ahorro suficiente para financiar las inversiones que requiere el progreso tecnológico que aumenta la productividad, y que aumenta la tasa de crecimiento del ingreso y la adaptación al calentamiento, y reduce la tasa de las emisiones de contaminantes de todas las fuentes de las actividades de consumo y producción.
La curva ambiental de la economía mundial y la restricción de la huella de carbono: una estimación de sus ecuaciones y sus efectos sobre el calentamiento global
Metodología del proceso de estimación: Ecuaciones, variables y datos
Según la teoría de la unificación de la huella de carbono y las emisiones per capitas con los fundamentos teóricos de la curva ambiental, ambas variables, expresadas como función del ingreso per cápita, deberían presentar una curva en forma de U invertida, es decir, deberían ser cóncavas al eje horizontal, explicando el tramo ascendente, el máximo, y el descendente de la curva en función del desarrollo tecnológico acelerador de la productividad de los factores, mitigador de los efectos del calentamiento, y ahorrador de emisiones de contaminantes.
Aunque esta sección está destinada a presentar y analizar una estimación de la validez de la tesis central ya enunciada, es necesario señalar las características del proceso metodológico y las restricciones de los datos usados en la referida estimación. En primer lugar, si el calentamiento global es el resultado de la acumulación de gases de efectos invernaderos en la atmosfera (medidos en CO2 equivalentes), en algún momento las restricciones de la cantidad de tierra necesaria para absolverlos y el aumento de los costos de reducir sus emisiones deberían reducir el crecimiento del ingreso. Dado que lo anterior solo puede ser observado y registrado con precisión a nivel de todo el planeta (los gases se emiten a nivel local, pero producen un efecto global) los datos a utilizar en la estimación deben ser los de la economía mundial. Se utilizan los datos del Banco Mundial del ingreso per cápita y de las emisiones de CO2, y de la Footprint network de la huella de carbono para el periodo 1961/2018.
En segundo lugar, hay que tomar en cuenta que el modelo de la unificación presentado en el capítulo tres no incluye una ecuación en la que la huella de carbono, o la de las emisiones per cápita, sean una función del ingreso per cápita, sino que dicha relación queda definida indirectamente por las variables explicativas de las ecuaciones fundamentales, según las tres etapas de la relación entre el crecimiento del ingreso y de las emisiones per capitas ya citadas y detalladas en el capítulo tres.
En tercer lugar, el efecto de la inversión en tecnologías aceleradoras de la productividad y reductoras de los efectos del calentamiento y de las emisiones de contaminantes tiene como mecanismos de transmisión el aumento de la formación bruta de capital y la reducción del consumo per cápita de energía, lo cual significa que, si la hipótesis sustentada tiene méritos suficientes, las variaciones de cada una de estas dos variables deben ser consistentes con las variaciones de las emisiones per capitas y el ingreso per cápita. Las ecuaciones estimadas fueron las siguientes:
en las que emiperc es la emisión per cápita, ingperc el ingreso per cápita, hcperc la huella de carbono per cápita, ceperc el consumo de electricidad per cápita, fbcperc la formación bruta de capital per cápita, y geiaa es la cantidad de gases de efecto invernadero acumulado en la atmosfera medidas en partes por millón.
El análisis preliminar mediante gráficos de dispersión mostró que en ningún caso la relación entre las variables era de tipo lineal, ni tampoco logarítmica o exponencial, sino que todos sugerían relación polinomial. Inicialmente las correlaciones fueron analizadas usando el programa Eview. Las regresiones fueron estimadas y las relaciones de cointegración fueron posteriormente fueron confirmadas y ampliadas con la asistencia de ChatGPT. (ChatGPT, OpenAI, 2025).
Se estimaron regresiones polinómicas no lineales para diversas combinaciones entre las variables explicadas y explicativas. Se identificaron los grados óptimos de ajuste para cada relación, considerando criterios de estabilidad, ajuste (R²) y evidencia de cointegración. A continuación, se resume el grado del modelo más adecuado para cada relación evaluada, la condición de cointegración y el valor de R cuadrado:
Tabla 1
Grado, condición de cointegración y correlación de las ecuaciones de regresión del modelo
Ecuación |
Grado del Polinomio |
¿Cointegración? |
R² |
emiperc ~ ingperc 1 |
5 |
Sí |
> 0.90 |
hcperc ~ ingperc. 2 |
5 |
Sí |
> 0.90 |
emiperc ~ ceperc. 3 |
6 |
Sí |
> 0.90 |
hcperc ~ ceperc. 4 |
6 |
No |
≈ 0.71 |
emiperc ~ fbcperc 5 |
6 |
Sí |
> 0.90 |
geiaa ~ ingperc. 6 |
3 |
Sí |
> 0.99 |
Como puede observarse, los modelos de grado 5 y 6 resultaron ser los más apropiados en cinco de las seis ecuaciones estimadas. No obstante, en otras como la ecuación 6, un polinomio de grado 3 ofreció un ajuste más robusto y estable. Esto evidencia la importancia de adaptar la complejidad del modelo a las características particulares de cada vínculo causal y estructural. El resumen de los resultados se presenta a continuación.
Regresiones Polinómicas No Lineales:
emiperc ~ ingperc (grado 5):
Ecuación: −0.8562·ingperc^0 + −0.4739·ingperc^1 + 1.2265·ingperc^2 + 0.8181·ingperc^3 + −0.2729·ingperc^4 + −0.1047·ingperc^5
R²: 0.8718
hcperc ~ ingperc (grado 5):
Ecuación: 0.1378·ingperc^0 + 2.0232·ingperc^1 + 0.0920·ingperc^2 + −1.1325·ingperc^3 + −0.0794·ingperc^4 + 0.2372·ingperc^5
R²: 0.8456
emiperc ~ ceperc (grado 6):
Ecuación: −0.6865·ceperc^0 + −1.0250·ceperc^1 + 1.9664·ceperc^2 + 2.0708·ceperc^3 + −1.3558·ceperc^4 + −0.5522·ceperc^5 + 0.3188·ceperc^6
R²: 0.9290
hcperc ~ ceperc (grado 6):
Ecuación: 0.3136·ceperc^0 + 0.8330·ceperc^1 + −1.4235·ceperc^2 + −0.2128·ceperc^3 + 1.1303·ceperc^4 + 0.1013·ceperc^5 + −0.2478·ceperc^6
R²: 0.7083
emiperc ~ fbcperc (grado 6):
Ecuación: −0.6694·fbcperc^0 + −0.1290·fbcperc^1 + 1.4822·fbcperc^2 + 0.8115·fbcperc^3 + −0.6680·fbcperc^4 + −0.1535·fbcperc^5 + 0.0946·fbcperc^6
R²: 0.8367
geiaa ~ ingperc (grado 3):
Ecuación: 0.0917·ingperc^0 + 0.9927·ingperc^1 + −0.1010·ingperc^2 + 0.0221·ingperc^3
R²: 0.9938
Prueba de Raíz Unitaria (ADF):
ingperc: ADF = 1.3429, p = 0.9968, Estacionaria: No
emiperc: ADF = −0.9119, p = 0.7840, Estacionaria: No
hcperc: ADF = −1.0069, p = 0.7508, Estacionaria: No
fbcperc: ADF = 0.3701, p = 0.9803, Estacionaria: No
ceperc: ADF = −0.1544, p = 0.9437, Estacionaria: No
geiaa: ADF = 3.1374, p = 1.0000, Estacionaria: No
Prueba de Cointegración (ADF sobre residuos):
emiperc ~ ingperc (grado 5): ADF = −4.4472, p = 0.0002, Cointegración: Sí
hcperc ~ ingperc (grado 5): ADF = −3.5773, p = 0.0062, Cointegración: Sí
emiperc ~ ceperc (grado 6): ADF = −3.7747, p = 0.0032, Cointegración: Sí
hcperc ~ ceperc (grado 6): ADF = −2.4875, p = 0.1185, Cointegración: No
emiperc ~ fbcperc (grado 6): ADF = −3.7641, p = 0.0033, Cointegración: Sí
geiaa ~ ingperc (grado 3): ADF = −3.9712, p = 0.0016, Cointegración: Sí
Modelos de Corrección de Errores (ECM):
emiperc ~ ingperc: Coef ΔX = 0.0006, p = 0.0000, Coef ECt−1 = −0.1842, p = 0.0546, R² = 0.614
hcperc ~ ingperc: Coef ΔX = 0.0002, p = 0.0201, Coef ECt−1 = −0.2502, p = 0.0364, R² = 0.241
emiperc ~ ceperc: Coef ΔX = 0.0014, p = 0.0000, Coef ECt−1 = −0.1550, p = 0.3476, R² = 0.385
emiperc ~ fbcperc: Coef ΔX = 0.0009, p = 0.0000, Coef ECt−1 = −0.1300, p = 0.1541, R² = 0.554
geiaa ~ ingperc: Coef ΔX = 0.0023, p = 0.0092, Coef ECt−1 = −0.0557, p = 0.2888, R² = 0.158
Pruebas de Causalidad de Granger:
ingperc → emiperc (rezago 2): p = 0.04827002035533666, Causalidad: Sí
ingperc → hcperc (rezago 2): p = 0.19001037110718305, Causalidad: No
ceperc → emiperc (rezago 2): p = 0.5297553665551015, Causalidad: No
fbcperc → emiperc (rezago 2): p = 0.03594128081868786, Causalidad: Sí
ingperc → geiaa (rezago 2): p = 0.913570617634028, Causalidad: No
Cointegración y relación de causalidad entre las variables de la curva ambiental y de la huella de carbono
Según los resultados de la prueba (ADF) de raíz unitaria, las variables de la ecuación 1 no son estacionarias, una de las condiciones necesarias para un análisis econométrico riguroso de series de tiempo. La ecuación de regresión de la ecuación 1 es la de un polinomio de quinto grado (Gráfico No. 5), presentando un coeficiente de correlación de 0.873, el cual se podría calificar como altamente significativo, tomando en cuenta el tipo de relación estructural entre el ingreso y las emisiones per capitas, así como el tipo regresión resultante.
Los resultados de la prueba de cointegración (Engle-Granger) arrojan un altísimo grado de cointegración entre el ingreso y las emisiones per-capitas. El modelo de corrección de errores aplicado muestra que cualquier desviación sobre la tendencia determinada por la cointegración es corregida en un periodo de 5.4 años. Por último, la prueba de causalidad de Granger indica que después de dos periodos, un cambio en el ingreso per cápita causa un cambio en las emisiones per-capitas.
Según los resultados de la prueba (ADF) de raíz unitaria, las variables de la ecuación 2 tampoco son estacionarias. La ecuación de regresión de la ecuación 2 es también la de un polinomio de quinto grado (Gráfico 6), presentando un coeficiente de correlación de 0.846, ligeramente inferior al de la ecuación 1 pero altamente significativo.
Los resultados de la prueba de cointegración (Engle-Granger) arrojan un alto grado de cointegración entre el ingreso y la huella de carbono per cápita, pero menor al existente entre el ingreso y las emisiones per capitas. El modelo de corrección de errores aplicado muestra que cualquier desviación sobre la tendencia determinada por la cointegración es corregida en un periodo de 4 años. Por último, la prueba de causalidad de Granger indica que no existe relación causal de ningún tipo entre la huella de carbono per cápita y el ingreso per cápita.
Como se puede observar en el Gráfico 6, la forma de la curva de ajuste es muy diferente a la de la curva ambiental del Gráfico 5 anterior, aunque ambas presentan cambios de pendientes durante todas sus trayectorias. La curva ambiental tiene forma clara de U invertida hasta un nivel aproximado de 7,500 dólares de ingresos per cápita, con un tramo descendente que empieza, en los alrededores de los 5,700 dólares de ingreso per cápita, valor en que según el modelo presentado en el capítulo tres, empezarían a registrarse los efectos de los aumentos de la inversión en aumento de la productividad y ahorro de emisiones.
Gráfico 5
Resultados del ajuste de las emisiones per capitas en función del ingreso per cápita en el caso de la ecuación de quinto grado
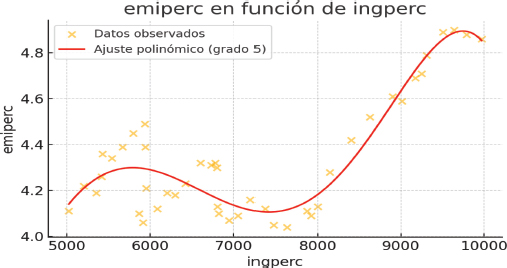
Gráfico 6
Resultados del ajuste de la huella de carbono per cápita en función del ingreso per cápita en el caso de la ecuación de quinto grado
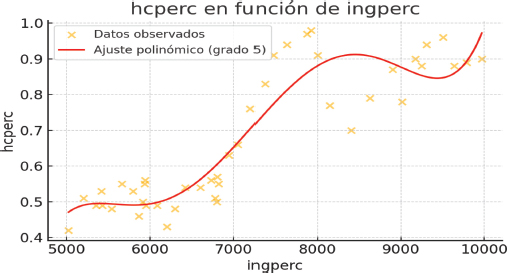
Pero a partir del valor aproximado de 7,500 dólares, la curva ambiental empieza a aumentar en vez de continuar disminuyendo, para luego presentar otro pequeño tramo descendente a partir de los 9,800 dólares de ingreso per cápita aproximadamente, el cual podría ser explicado por el hecho de que a partir de cierto nivel de ingreso, el aumento de la riqueza que produce el crecimiento permanente del mismo podría provocar un aumento del consumo y reducir el ahorro que financia la inversión ahorradora de emisiones, haciendo que las mismas se coloquen en una trayectoria de crecimiento igual al del ingreso per cápita. Adicionalmente, dado el crecimiento permanente del ingreso, llegaría un momento en que los consumidores valorarían la calidad ambiental como un bien superior altamente deseable, lo que también aporta poder explicativo del segundo tramo descendente de la curva ambiental.
La forma de la curva de la huella presenta una relación muy diferente a la de la emisión per cápita. Sin embargo, mientras la curva de las emisiones presenta forma de dos U invertidas, la de la huella presenta solo una, y menos intensa. A pesar de la relación de equivalencia entre las dos variables, las ecuaciones de ajuste muestran que mientras en el tramo comprendido entre los 8,500 y los 9,500 dólares la emisión per cápita tiende a crecer, la huella per cápita tiende a lo contrario.
La energía renovable, la eficiencia energética y la formación bruta de capital
Los Gráficos No. 7 y 8 presentan las curvas de ajuste de las ecuaciones de regresión polinómicas de sexto grado correspondiente a las emisiones per capitas y el consumo de energía per cápita (medido en KWh por persona) y la formación bruta de capital per cápita, respectivamente. La prueba ADF arrojó que ninguna de dichas variables es estacionaria. Los valores de R cuadrado son 0.93 y 0.84, respectivamente. Las pruebas realizadas reflejaron una altísima probabilidad de cointegración entre las variables de ambas ecuaciones.
Gráfico 7
Resultados del ajuste de las emisiones per capitas en función del consumo de energía per cápita en el caso de la ecuación de sexto grado
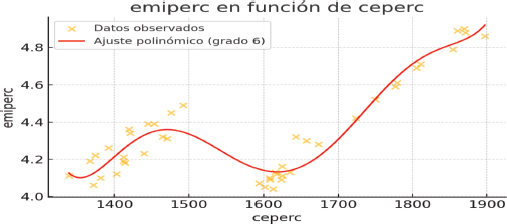
Gráfico 8
Resultados del ajuste de las emisiones per capitas en función de la formación bruta de capital per cápita en el caso de la ecuación de sexto grado
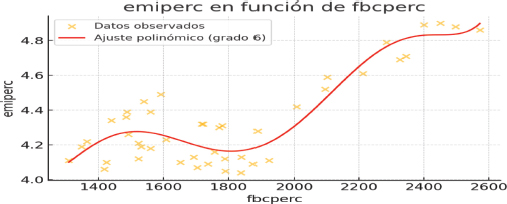
Los modelos de corrección de errores reflejaron que cualquier desviación con respecto a la tendencia de largo plazo es corregida en aproximadamente siete periodos. La forma de estas dos curvas es totalmente consistente con la forma de la curva ambiental del Gráfico 4, pues al igual que esta, ambas presentan un primer tramo en forma de U invertida, con valores de máximo y mínimo de emisiones per capitas en la parte descendente casi exactamente iguales en las tres curvas, lo cual significaría que el efecto de la formación bruta de capital, el aumento de las energías de fuentes renovables y la eficiencia energética son mecanismos de transmisión que aceleran el crecimiento del ingreso al tiempo que reducen las emisiones per capitas.
Adicionalmente, la fuerte similitud entre las tres curvas apoya de manera robusta la hipótesis de que el efecto riqueza que se produce a partir de cierto nivel del ingreso per cápita produce un desplazamiento hacia arriba de la curva del consumo, y por ende, una disminución del ahorro que financia la inversión en tecnología aceleradora de la productividad y reductora de las emisiones, generando un nuevo ciclo de aumento en las emisiones per capitas.
Cointegración entre crecimiento y gases de efectos invernadero acumulados en la atmosfera generadores del calentamiento global
La huella de carbono per cápita es un cálculo que representa la cantidad de tierra necesaria para absorber la cantidad de CO2 que emite cada persona en sus actividades de producción y consumo. Si la cantidad de tierra destinada a tales fines es menor que la requerida, lo emitido será mayor que lo absorbido, y la diferencia iría a acumularse en la atmosfera, aumentado el calentamiento global del planeta. Si la cantidad de tierra (capital natural destinado a la producción de servicios ecosistémicos, ecuación 6 del modelo del capítulo tres) destinada a la absorción permanece fija, y también todas las demás variables, entonces todo aumento del consumo producirá un aumento de las emisiones netas que irían a parar a la atmosfera.
Lo anterior significa que debería existir una fuerte relación entre la cantidad de gases de efecto invernadero acumulado en la atmosfera y el ingreso per cápita. La curva del Gráfico 9 presenta la ecuación de regresión polinómica de tercer grado entre ambas variables. El valor de R cuadrado es de 0.99 y las pruebas revelan la existencia de una altísima cointegración entre ambas variables.
Gráfico 9
Gases de efectos invernaderos acumulados en la atmosfera en función del ingreso per cápita.
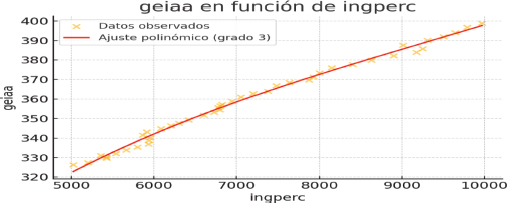
El modelo de corrección de errores obtenidos demuestra que cualquier desviación del ingreso sobre su efecto de largo plazo en la acumulación de gases de efecto invernadero tarda un total de 18 años para corregirse, lo cual debería ser un factor fundamental para tomar en cuenta a la hora de fijar la tasa de descuento con la cual se calcularían los efectos de las emisiones presentes sobre el ingreso futuro. El hecho de que esta curva sea ascendente en todas sus partes tiene una implicación fundamental: aunque la curva ambiental existe (según las evidencias presentadas, pero no exactamente en forma de U invertida), la misma no tiene ninguna incidencia en el proceso de acumulación de gases de efecto invernadero en la atmosfera causantes del calentamiento global.
Los escenarios de calentamiento global y los costos de reducción de las emisiones per-capitas consistente con un aumento de la temperatura de 1.5 grados
La diferencia entre el costo del calentamiento global y del de la amortización de la inversión necesaria para la reducción de las emisiones per capitas podría ser el factor decisivo para la aceleración de la esta. Según el marco teórico de la sección 3.4 del capítulo tres, y según las conclusiones del sexto informe (AR6) del Intergubernamental Panel Climate Change (IPCC, 2023), dada la cantidad actual de gases de efectos invernadero acumulada en la atmosfera (determinante del costo del calentamiento global), el costo actual marginal de emitir es mucho mayor que el costo marginal de reducir, de lo cual constituye un ejemplo la fuerte trayectoria descendente de los costos de la energía de fuentes renovables no emisoras de CO2.
Para estimar el impacto del crecimiento estimado en el modelo, hay que partir de que el mismo vincula el ingreso per cápita con el calentamiento global de la siguiente manera: a) El ingreso per cápita influye en el nivel de emisiones de CO₂ per cápita, generalmente de manera no lineal. b) Parte de estas emisiones se acumula en la atmósfera, elevando la concentración global de CO₂ (ppm). c)Esta mayor concentración provoca un incremento en la temperatura global promedio, según una relación logarítmica establecida por la física climática.
Las relaciones clave se expresan en las siguientes ecuaciones:
Emisiones percápita como función del ingreso (modelo polinómico):
Acumulación de CO₂ en la atmósfera (ppm):
GEIAAt = GEIAAt−1 + (θ · EmiPerct · Pt) / (2.13 × 10³)
donde θ ≈ 0.45 representa la fracción de CO₂ que permanece en la atmósfera, y Pt es la población mundial (en millones).
Aumento de temperatura global asociado a concentración de CO₂:
ΔTt = λ · ln(GEIAAt / 280)
donde λ es la sensibilidad climática (≈ 2.5 a 4.5 °C por duplicación del CO₂) y 280 ppm es la referencia preindustrial.
Ecuación integrada que conecta ingreso per cápita con su efecto de largo plazo en el calentamiento global:
Esta ecuación integrada ha sido aplicada a las trayectorias de ingreso y población para estimar el comportamiento de GEIAA y, en consecuencia, el calentamiento simulado por el modelo, el cual no es exactamente igual a la temperatura de equilibrio según los efectos de largo plazo del forzamiento radioactivo.
Este modelo se aplica tomando como referencia las trayectorias de los Escenarios Socioeconómicos Compartidos (SSP) del IPCC. Cada escenario (SSP1 a SSP5) proyecta una evolución diferente del ingreso global, la población y las emisiones, lo cual permite alimentar el modelo con supuestos específicos para evaluar sus consecuencias sobre la acumulación de gases de efecto invernadero y el incremento de la temperatura promedio global. Se han seleccionados los siguientes escenarios:
- SSP1 (Sostenibilidad): proyecta un crecimiento económico moderado con fuertes políticas ambientales, resultando en emisiones decrecientes compatibles con el tramo descendente de la CAK
- SSP2 (Trayectoria intermedia): crecimiento y mitigación moderados, pero con mayor población, lo que se alinea con una curva de Kuznets suavemente invertida.
- SSP5 (Desarrollo impulsado por combustibles fósiles): altos niveles de ingreso, pero con aumento continuo de emisiones, reflejando una curva ambiental no revertida.
Las simulaciones requieren que cada SSP sea asociado a una Trayectoria Representativa de Concentraciones (RCP, por sus siglas en inglés) determinantes de los valores del forzamiento radioactivo, determinante a su vez del aumento de la temperatura a través del factor de sensibilidad climática de largo plazo, λ = 0.8 °C/W·m². La ecuación integrada ha sido aplicada a estas trayectorias de ingreso y población para estimar el comportamiento de los GEIAA y, en consecuencia, el calentamiento esperado bajo distintos supuestos de política y tecnología. Esta aproximación permite analizar si el crecimiento económico proyectado bajo ciertos SSP será ambientalmente viable sin romper los umbrales críticos de calentamiento (por ejemplo, 1.5 °C o 2 °C). A continuación, se presenta una simulación cuantitativa con base en el modelo integrado y las proyecciones al año 2050 de tres los escenarios socioeconómicos compartidos del IPCC seleccionados (SSP1, SSP2 y SSP5) asociados a las trayectorias representativas de concentraciones determinantes de forzamiento radioactivo de 2.6, 4.5 y 8.5 W/m, según se indica después del guion:
Tabla 2
Resumen resultados de los escenarios socioeconómicos compartidos arrojados por el modelo
Escenario |
Ingreso per cápita (USD) |
Población (millones) |
Emisiones pc (tCO₂) |
Emisiones totales (GtCO₂) |
GEIAA (ppm) |
ΔT (°C) |
SSP1–2.6 |
22,000 |
8,500 |
3.28 |
27.86 |
417.89 |
1.49 |
SSP2–4.5 |
18,000 |
9,200 |
4.90 |
45.08 |
419.52 |
1.53 |
SSP5–8.5 |
32,000 |
8,700 |
8.80 |
76.56 |
423.17 |
1.60 |
Como se puede observar, a mayor ingreso per cápita se proyectan mayores emisiones y, por tanto, un mayor calentamiento, especialmente en escenarios sin políticas climáticas ambiciosas. El escenario SSP5 muestra el mayor incremento de temperatura (1.60 °C), superando el umbral crítico de 1.5 °C, mientras que SSP1 se mantiene por debajo, gracias a su énfasis en sostenibilidad. Estos resultados ilustran cómo el diseño de políticas puede modificar las trayectorias del calentamiento global.
Un resultado muy importante de este estudio es que la relación empírica entre las emisiones per cápita (EmiPerc) y el ingreso per cápita (Y) estimada mediante una regresión polinómica de quinto grado presenta una forma en U invertida consistente con la hipótesis de la Curva Ambiental de Kuznets (CAK). El análisis muestra que las emisiones aumentan con el ingreso hasta un umbral de aproximadamente 7,500 dólares, luego disminuyen, pero experimentan un repunte leve al acercarse a los 9,800 dólares, seguido por una estabilización o ligera reducción. Este patrón sugiere que, si bien existe una tendencia a la desvinculación entre crecimiento económico e impacto ambiental, esta no es estrictamente lineal ni irreversible. Más bien, indica una posible doble fase o estructura ondulante, posiblemente influida por factores como el consumo creciente, las mejoras tecnológicas, o las políticas ambientales. Este resultado fortalece el uso de modelos de evaluación integrados y plantea la necesidad de políticas diferenciadas según el nivel de ingreso.
Según el sexto informe (AR6) del IPCC (2023, op. cit.), la inversión necesaria para alcanzar el objetivo de limitar el calentamiento a 1.5 °C estaría en el rango de 2%–4% del PIB mundial anual, mientras que el costo estimado de la inacción climática estaría entre 5% y hasta 20% del PIB mundial anual, lo cual significa que la relación beneficio/costo de la inversión en reducción de las emisiones estaría entre 2.5 y 5 unidades de PIB mundial.
Sin embargo, hay que tener pendiente que las inversiones en reducción de las emisiones se realizan en el presente, y se amortizan en el futuro a una tasa de descuento determinada, y que los beneficios representados por el costo del calentamiento global evitado se reciben también en el futuro, razón por la cual también deben ser descontados a esa misma tasa de descuento. Pero la inversión requerida, y mucho más los beneficios de la misma, están sujetos a un amplio margen de incertidumbre propios de los Modelos de Evaluación Integrada (Allegue Losada, Y., 2010), y más aún, los resultados siempre son altamente sensibles a pequeñas variaciones de la tasa de descuento, y el cálculo de la relación beneficio/costo, depende de dicha tasa de descuento.
La mejora de las técnicas de los modelos de estimación de los impactos del calentamiento global, así como de la precisión para determinar la tasa de descuento a utilizar para estimar costos y beneficios futuros de las inversiones necesarias para alcanzar la meta de un aumento máximo de 1.5 grados de temperatura, debería ser el primer gran punto de la agenda de investigación a seguir en los próximos años. El efecto de la inversión en la reducción del calentamiento global dependerá de la capacidad de las políticas ambientales mundiales, definidas y aplicadas por todos los países y gobiernos, para lograr que los costos y los beneficios, que se manifiestan en formas de externalidades positivas y negativas, sean internalizadas por los consumidores y productores de todo el planeta, y ese quizás podría ser el segundo gran punto de la agenda de investigación de corto plazo.
Conclusiones e implicaciones para la agenda de investigación sobre el cambio climático: el déficit de la huella de carbono no ha sido, pero podría ser una restricción al crecimiento sostenible
Los principales resultados presentados en los capítulos anteriores pueden resumirse en cinco grandes conclusiones: En primer lugar, la curva ambiental de la economía mundial existe, tanto para las emisiones como para la huella de carbono per cápita, pero en el caso de las emisiones per capitas, en vez de forma de U invertida, tiene forma de M leve y poco pronunciada, con dos ciclos de tramos ascendentes y descendentes. Los resultados demuestran de manera robusta que el ingreso y las emisiones per capitas están cointegradas, y que existe una relación de causalidad desde la primera variable a la segunda. En el caso de la huella de carbono, el tramo descendente de la curva ocurre a un nivel de ingreso mucho mayor que el de las emisiones, lo que significa que las emisiones per capitas empiezan a reducirse mucho antes de que se inicie el aumento de la cantidad y productividad de la tierra disponible para la absorción de dichas emisiones.
En segundo lugar, los resultados demuestran que la restricción de la cantidad de tierra en que se fundamenta la huella ecológica no ha restringido el proceso de crecimiento de crecimiento del ingreso per cápita mundial. La inversión que aumenta la productividad amortigua el efecto del calentamiento y reduce las emisiones; la regulación gubernamental de las emisiones de contaminantes, y el hecho de que la calidad ambiental es un bien superior para los consumidores mundiales, son causales que estarían determinando que el crecimiento del ingreso permanezca siendo sostenible, y que la economía mundial haya escapado de la restricción que impone una cantidad fija de tierra.
En tercer lugar, el hecho de que la cantidad de tierra determinada por la huella no haya sido una restricción al crecimiento del ingreso per cápita no significa que no lo pueda ser. La cantidad de gases de efecto invernadero acumulado en la atmosfera continúa aumentando. La discusión científica en torno a la viabilidad de lograr el objetivo de que la temperatura promedio no exceda a 1.5 grados al de era preindustrial resume la preocupación en torno a la posibilidad de que en algún momento el calentamiento global produzca una reducción o paralización del crecimiento.
En cuarto lugar, aunque la curva ambiental de Kuznets exista en términos estadísticos y causales, su existencia no niega la del aumento del calentamiento global, el cual también se encuentra debidamente acreditado por los datos empíricos. El que las emisiones per capitas no aumenten no significa que no estén aumentando la cantidad de gases de efectos invernaderos acumulados en la atmosfera, lo cual es la causa, según el estado del arte del conocimiento científico, del calentamiento global.
En quinto lugar, el hecho de que un aumento de las emisiones de CO2 produce efectos sobre la acumulación de CO2 en la atmosfera en un periodo de tiempo menor a 20 años es una evidencia que debería aumentar la preocupación de la humanidad por los impactos futuros del cambio climático. Mantener el estado del bienestar actual para transmitirlo a las generaciones futuras dependerá de la capacidad de todo el mundo de mantener el actual ingreso per cápita si aumentar la cantidad de gases de efecto invernadero acumulado en la atmosfera.
De las conclusiones anteriores se derivan dos grandes implicaciones que deberían ser tomadas en cuenta en la agenda de investigación sobre la relación entre emisiones, huella de carbono y cambio climático. En primer lugar, la literatura revisada en el capítulo uno es clara en cuanto al planteamiento teórico fundamental de la sostenibilidad débil: Dado que existe una tasa de sustitución entre el capital físico y el natural, siempre que la renta proveniente de la explotación del capital natural (la renta del uso de la tierra para fines agrícolas en vez de su uso en la producción de servicios ecosistémicos) se invierta en capital físico, el crecimiento podría continuar inalterado. El mayor volumen de capital físico a que conduciría la tasa de sustitución de capital natural por capital físico debería conducir a un aumento en la tasa de emisiones per capitas (según las ecuaciones fundamentales del modelo presentado en la sección tres), razón por la que la sostenibilidad débil no sería compatible con la existencia de la curva ambiental.
Pero si se acepta que la renta proveniente del uso del capital natural puede ser invertido en capital físico portador de tecnología aceleradora de la productividad, amortiguador de los efectos del calentamiento y ahorradora de emisiones, entonces la citada compatibilidad si pudiera existir, y los resultados obtenidos y presentados en el capítulo anterior apoyan este planteamiento. Sin embargo, aunque la curva ambiental y la sostenibilidad débil pueden existir simultáneamente, dicha existencia significa, esencialmente, que una cantidad fija de tierra no ha sido una restricción al crecimiento del ingreso per cápita, y que una mayor participación del capital físico en el total puede producirse al mismo tiempo que una reducción de las emisiones per capitas.
En segundo lugar, si la acumulación de gases de efectos invernadero en la atmosfera es un pasivo ambiental cuyo saldo produciría una reducción futura del ingreso per cápita, entonces el asunto fundamental seria la identificación de alternativas para reducir ese pasivo mediante las amortizaciones que significan menores tasas de crecimiento actual del ingreso, de forma tal que se reduzca el crecimiento del pasivo y no se produzcan las condiciones que obligarían a saldarlo en su totalidad, lo que conduciría a una reducción del ingreso per cápita mundial de manera súbita.
Para reducir el pasivo ambiental mundial hay que invertir, y el tramo descendente de la curva de ajuste presentada en el Gráfico 7 demuestra que dicha inversión puede tener efecto importante y duradero en la reducción de las emisiones per capitas. Pero la inversión en tecnología ahorradora de emisiones de CO2 está asociada a dos procesos fundamentales, el primero de los cuales es el tránsito hacia una economía mundial menos intensiva en carbono, la transición energética hacia energía de fuentes renovables, y el aumento de la circularidad y de la eficacia en el uso de materiales y recursos naturales.
Los costos del calentamiento global y el cambio climático lo pagarán los consumidores y productores, pero no se puede predecir, con un alto nivel de confianza, que serán los actuales o los de las nuevas generaciones, o un grupo compuesto por ambas. Dado que los costos y beneficios de reducir y aumentar las emisiones los reciben o recibirán productores y consumidores, el segundo proceso necesario para aumentar la inversión en tecnología ahorradora de emisiones está asociado al tránsito hacia un patrón de consumo menos carbono/intensivo, que conduzca a inversiones en empresas con cartera de productos también más sostenible.
El cumplimiento de los compromisos de las contribuciones nacionales determinadas y de los demás acuerdos mundiales para la reducción de los gases de efectos invernaderos que evitarían un aumento promedio mayor de 1.5 grados del calentamiento global solo pueden lograrse si se acelera de manera significativa la efectividad de las inversiones y el progreso tecnológico en la reducción de las emisiones per capitas, y aumenta la productividad de la tierra en la producción de bienes y servicios ecosistémicos que absorben las emisiones de CO2, para lo cual es necesario que los gobiernos, los consumidores y los productores internalicen una función de costo del calentamiento global mayor que la amortización de la inversión necesaria reducir las emisiones per capitas.
Bibliografia citada
Ali, M., Lin, B., & Adebayo, T. (2024). Assessing sustainable growth pathways through the EKC and SSP frameworks. Nature Sustainability. https://doi.org/10.1038/s41893-024-01123-
Allegue Losada, Y. (2010). Modelos de evaluación integrada del impacto del cambio climático: Algunas consideraciones sobre un modelo para la región del Caribe. Economía y Desarrollo, 145(1–2), 237–264.
Correa Restrepo, F. (2015). Economía del desarrollo sostenible: Propuestas y limitaciones de la teoría neoclásica. Semestre Económico, 6(12). https://revistas.udem.edu.co/index.php/economico/article/view/1367
Destek, M. A., Ulucak, R., & Dogan, E. (2018). Análisis de la curva ambiental de Kuznets para los países de la UE: el papel de la huella ecológica. MPRA Paper 106882. University of Munich.
Fang, X., Zhou, B., Tu, X., Ma, Q., & Wu, J. (2018). What kind of a science is sustainability science? An evidence-based reexamination. Sustainability, 10, 1478.
Grossman, G. M., & Krueger, A. B. (1991). Impactos ambientales de un Tratado de Libre Comercio de América del Norte. Documentos 158, Princeton University.
Grossman, G. M., & Krueger, A. B. (1995). Economic growth and the environment. The Quarterly Journal of Economics, 110(2), 353–377.
Guillo, M. D., & Magalhaes, M. (2018). Long-run sustainability in the Green Solow Model. WP # 18-02. Universitat d’Alacant.
IPCC. (2023). Climate Change 2023: Synthesis Report. IPCC. https://doi.org/10.59327/IPCC/AR6-9789291691647
Kaika, D., & Zervas, E. (2013). The Environmental Kuznets Curve (EKC) theory—Part A: Concept, causes and the CO₂ emissions case. Energy Policy, 62, 1392–1402. https://doi.org/10.1016/j.enpol.2013.07.131
Konya, S. (2022). Estimación de panel de la curva ambiental de Kuznets para emisiones de CO₂ y huella ecológica: Sostenibilidad ambiental en países en desarrollo. Folia Oeconomica Stetinensia, 22(2), 123–145.
Lazăr, D., Minea, A., & Purcel, A.-A. (2019). Contaminación y crecimiento económico: Evidencia de países de Europa central y oriental. Energy Economics, 81, 1121–1131.
Lenuta, C., Banacu, C. S., & Busu, M. (2019). Environmental factors and sustainability of the circular economy model at the European Union level. Sustainability, 11, 1114. https://doi.org/10.3390/su11041114
OpenAI. (2025). ChatGPT (Versión del modelo [ej. GPT-4o]) [Modelo de lenguaje de gran tamaño]. https://chat.openai.com
Palmero, F. M. (2004). Desarrollo sostenible y huella ecológica. Netbiblio.
Pata, U. K., & Balsalobre-Lorente, D. (2022). Exploring the impact of tourism and energy consumption on the load capacity factor in Turkey: A novel dynamic ARDL approach. Environmental Science and Pollution Research, 29, 13491–13503. https://doi.org/10.1007/s11356-021-16675-4
Reyes, R. (2019). Costo de oportunidad, valor ecosistémico y optimización del uso de la tierra. Ciencia, Economía y Negocios, 3(2), 43–60. https://doi.org/10.22206/ceyn.2019.v3i2.pp43-60
Sahu, S. K., & Shatrunjay, A. (2017). An alternative argument of Green Solow Model in developing economy context. Working Paper 160, Madras School of Economics.
Sarkodie, S. A., & Strezov, V. (2019). A review on Environmental Kuznets Curve hypothesis using bibliometric and meta-analysis. Science of The Total Environment, 649, 128–145. https://doi.org/10.1016/j.scitotenv.2018.08.276
Schiliro, D. (2019). Sustainability, innovation, and efficiency: A key relationship. MPRA Paper 96852. https://mpra.ub.uni-muenchen.de/id/eprint/96852
Stern, D. I. (2015). The environmental Kuznets curve after 25 years. CCEP Working Paper 1514, Crawford School of Public Policy. https://ssrn.com/abstract=2737634
Stern, N. (2006). Stern review on the economics of climate change. Cambridge University Press. http://www.sternreview.org.uk
Tiba, S., & Omri, A. (2017). Estudio de la literatura sobre las relaciones entre energía, medio ambiente y crecimiento económico. Renewable and Sustainable Energy Reviews, 69, 1129–1146.
Usman, M., & Makhdum, M. S. A. (2021). ¿Qué reduce la huella ecológica en la región BRICS-T? Exploración de la influencia de la energía renovable, la energía no renovable, la agricultura, la superficie forestal y el desarrollo financiero. Renewable Energy, 179, 28–41.
Wackernagel, M., & Rees, W. (1996). Nuestra huella ecológica: Reducir el impacto humano en la Tierra. New Society Publishers.
Wang, J., Liu, Q., & Chen, M. (2023). Linking carbon footprint and economic growth under the EKC framework: A global perspective. Journal of Cleaner Production, 387, 135742. https://doi.org/10.1016/j.jclepro.2023.135742
Yandle, B., Bhattarai, M., & Vijayaraghavan, M. (2004). Curvas ambientales de Kuznets: Una revisión de hallazgos, métodos e implicaciones políticas. IWMI Research Reports H044740, International Water Management Institute.
Zhang, Y., Li, W., & Zhao, X. (2022). Environmental Kuznets Curve for CO₂ emissions in G20 countries: Evidence from dynamic panel threshold modeling. Energy Economics, 110, 105944. https://doi.org/10.1016/j.eneco.2022.105944
_______________________
1 Universidad Agroforestal Fernando Arturo de Meriño. ORCID: 0000-0001-7160-5961. Correo-e: rolando.reyes@uafam.edu.do
