Ciencia, Economía y Negocios, Vol. 7, No. 2, julio-diciembre, 2023 ISSN (impreso): 2613-876X • ISSN (en línea): 2613-8778 • Sitio web: https://revistas.intec.edu.do/
IDENTIFICACIÓN DEL RIESGO SISTÉMICO EN LA BANCA MÚLTIPLE: UN ENFOQUE DE REDES BIPARTITAS
Identification of Systemic Risk in a Multiple Banking System: A Bipartite Networks Approach
DOI: https://doi.org/10.22206/ceyn.2023.v7i2.2948
PETRA M. GOICO CASTILLO1
FELIPE LLAUGEL2
1 Instituto Tecnológico de Santo Domingo (INTEC), República Dominicana. Correo-e: 1102810@est.intec.edu.do
2 Instituto Tecnológico de Santo Domingo (INTEC), República Dominicana. Correo-e: felipe.llaugel@intec.edu.do
Recibido: 27/07/2023 • Aprobado: 17/10/2023
Cómo citar: Goico Castillo, P. M., & Llaugeul, F. (2023). Identificación del Riesgo Sistémico en la Banca Múltiple: un enfoque de Redes Bipartitas. Ciencia, Economía y Negocios, 7(2), 5-32. https://doi.org/10.22206/ceyn.2023.v7i2.2948
Resumen
El sistema financiero puede representarse como una gran red compleja en la que los bancos están interconectados entre sí a través de vínculos financieros visibles e invisibles. En este trabajo se presenta un modelo que permite analizar un sistema financiero mediante un enfoque de teoría de redes, el cual constituye una herramienta práctica de monitoreo y diagnóstico para entes reguladores al permitir identificar las vulnerabilidades que surgen a medida que los bancos se vuelven cada vez más interconectadas, un choque en una red financiera puede provocar importantes fallas en cascada en todo un sistema, en otras palabras, riesgo sistémico. Para estudiar el riesgo sistémico del sector financiero dominicano, se crea un modelo de red financiera bipartita compuesto por dos tipos de nodos, (i) bancos múltiples (o comerciales) y (ii) cartera de crédito -segmentada por sector económico-, el cual prueba la influencia de cada crédito en particular o grupo de créditos en los bancos múltiples en general, y se implementa una prueba de estrés para evaluar la vulnerabilidad de la red ante el impacto en la cartera de crédito como consecuencia de sucesos externos en los distintos sectores económicos del país.
Palabras clave: Riesgo sistémico; redes financieras bipartitas; contagio, regulación macroprudencial; prueba de estrés.
Clasificación JEL: D85, E51, G21, G28.
Abstract
The financial system can be represented as a large complex network in which banks are interconnected with each other through visible and invisible financial links. This paper presents a model that allows analyzing a financial system through a network theory approach, which constitutes a practical monitoring and diagnostic tool for regulatory entities by allowing the identification of vulnerabilities that arise as banks become increasingly most interconnected, a crash in a financial network can cause major failures to cascade throughout an entire system, in other words, systemic risk. To study the systemic risk of the Dominican financial sector, a bipartite financial network model was construct, that is composed of two types of nodes, (i) commercial banks and (ii) bank credit portfolio -segmented by economic sector-, which tests the influence of each credit in particular or group of credits in commercial banks in general, and a stress test was implemented to assess the vulnerability of the network before the impact on the credit portfolio as a consequence of external events in the different economic sectors of the country. This document explores the use of the interconnection of financial networks to detect financial difficulties, as an early warning system with applications to macroprudential policy.
Keywords: Systemic risk; bi-partite financial network; contagion; macro-prudential regulation; stress test.
JEL codes: D85, E51, G21, G28.
Introducción
La crisis financiera de 2007-2008 cambió el enfoque de las autoridades reguladoras y supervisoras de banco ‘demasiado grande para fallar’ (Too-Big-to-Fail) a ‘demasiado conectado para fallar’ (Too-Connected-to-Fail) (Chan-Lau, 2010; Aldasoro, Gatti & Faia, 2016). Tras la experiencia de la crisis, se evidenció la importancia del riesgo de interconexión entre las entidades por la materialización que produjo, manifestando la necesidad de profundizar el estudio de las causas de la inestabilidad de los sistemas financieros y demostrando las limitaciones de las herramientas y metodologías convencionales para mitigar los efectos adversos del riesgo sistémico (Chavarría, 2014). El contagio se produce a través de diferentes canales, incluidos (i) el riesgo de contraparte y (ii) las tenencias de activos comunes, entre estos, las carteras de crédito. De estos, el primero ha recibido hasta ahora la mayor atención, aunque muchos creen que el problema principal se debe al segundo (Caccioli et al., 2014).
El riesgo sistémico es un término que se refiere a la posibilidad de que un problema en una parte del sistema financiero se propague y cause un daño importante que lo paralice o impida en forma significativa su funcionamiento. Esto puede ocurrir si una entidad o conjunto de estas presentan dificultades, como la falta de cumplimiento de sus obligaciones y si estos problemas se trasmiten a otras entidades sanas, llevándolas a la quiebra.
La prevención y mitigación del riesgo sistémico son importantes para garantizar la estabilidad y la resiliencia del sistema financiero. Para evitar el efecto contagio y la consecuencia del riesgo sistémico, las autoridades reguladoras y supervisoras del sistema necesitan herramientas para detectar, por ejemplo, el riesgo de incumplimiento de los deudores crediticios por impactos en el sector económico en el que se desenvuelven, en una o varias entidades que podría iniciar una reacción en cadena que haga que las entidades sanas sean arrastradas por las no sanas.
El sistema financiero dominicano está compuesto, en la actualidad, por 45 entidades de intermediación financiera, las cuales se dividen en los subsectores de bancos múltiples, asociaciones de ahorros y préstamos, bancos de ahorro y crédito y corporaciones de crédito. Como parte de los activos financieros, se encuentra la cartera de créditos (más del 50%), dicha cartera se concentra en el subsector de la banca múltiple en más del 80%. El riesgo sistémico es sensible al desempeño de estas entidades, razón por la cual la Autoridad Bancaria y Financiera, compuesta por el Banco Central y la Superintendencia de Bancos, requiere de reportes de forma periódica para monitorear y desarrollar herramientas de vigilancia del sistema financiero, con especial interés en los bancos múltiples.
Los bancos que poseen carteras de crédito con deudores en común también podrían quebrar o ser arrastrados ante una incapacidad de estos deudores cumplir con sus obligaciones, a causa de eventos que impacten el sector económico en el que desempeñan sus actividades productivas. El daño en la red bancaria podría continuar extendiéndose y el resultado es una cascada de propagación del riesgo en todo el sistema financiero.
En este trabajo se construye una red bancaria bipartita compuesta por dos tipos de nodos, (i) los bancos múltiples y (ii) la cartera de crédito, de los bancos para medir la causalidad entre los nodos de la red usando la matriz de incidencia, para probar la importancia relativa o peso que tienen los créditos de un banco en los créditos de otro banco y viceversa, que pueda promover el riesgo de contagio.
Esta herramienta detectará los posibles vínculos que existe entre una entidad y una cartera de crédito de acuerdo al sector económico en el que se desenvuelve el deudor, y así, probar la influencia de cada crédito en particular o grupo de créditos en el sistema financiero general, por ejemplo, si los créditos al sector agrícola o turismo caen en un 50% a cartera morosa, podemos estudiar qué bancos podrían ser vulnerables a la quiebra y ofrecer sugerencias de políticas regulatorias para evitar tal falla, como el requisito de reducir la exposición a los préstamos agrícolas o monitorear de cerca a los bancos expuestos.
A los fines de este trabajo, se propone el uso de la cartera de créditos como buen parámetro para medir el impacto de riesgo sistémico. A los fines de que, la cartera de créditos de un banco es una variable importante porque representa la principal fuente de ingresos y ganancias para la mayoría de los bancos. Además, la cartera de créditos puede reflejar la estrategia de negocio del banco y su exposición al riesgo crediticio. Por lo tanto, al construir una red bipartita basada en la cartera de créditos, se pueden analizar las relaciones entre los bancos y los prestatarios, lo que puede proporcionar información valiosa sobre la interconexión de los bancos y su riesgo sistémico, lo que puede ser útil para predecir futuras crisis financieras y diseñar políticas regulatorias adecuadas.
1. Planteamiento del problema
1.1 Objetivo general
Este trabajo tiene por objeto proporcionar una herramienta práctica de monitoreo y diagnóstico para el regulador, basada en la información habitual proporcionada por los bancos múltiples en su conjunto, que se focaliza en identificar las vulnerabilidades que pudiera inducir al riesgo sistémico aplicando un enfoque de redes financieras bipartitas.
1.2 Objetivos específicos
Para alcanzar este objetivo general, se definen los siguientes objetivos específicos:
EO1.Construir una red bancaria bipartita compuesta de dos tipos de nodos, (i) bancos y (ii) cartera de créditos -segregada por sectores económicos. El vínculo entre un banco y una cartera de crédito existe cuando el banco tiene la misma cartera con el mismo sector económico en su balance.
EO2.Crear matriz de incidencia de la cartera de créditos por sector económico y entidades.
EO3.Emplear prueba de estrés.
EO4.Aplicar métricas para comparar los resultados de la red.
1.3 Justificación
El sistema financiero desempeña un rol de importancia en el desarrollo económico de los países llevando a cabo procesos de intermediación financiera, mediante su actuación como intermediarios entre los prestamistas y los prestatarios para canalizar los recursos de una parte a otra. La principal finalidad de la intermediación financiera es captar los recursos de los depositantes y colocarlos a disposición de los prestatarios que necesitan financiamiento para invertir en proyectos productivos o personales (Cadavid, 2019).
Con el crecimiento en la demanda de financiamientos por parte de los prestatarios, las entidades financieras han acrecentado su influencia en el desarrollo de los distintos sectores económicos de los países, ejerciendo un papel fundamental en la economía al mejorar la eficiencia en el mercado financiero y reduciendo los costos de transacción para los prestatarios y los prestamistas. Además, los intermediarios financieros ayudan a reducir el riesgo de impago de los prestatarios a través de la evaluación de crédito, lo que aumenta la confianza de los prestamistas en el mercado financiero.
Como señala Santana, M. (2015, p. 23), “en la medida que el sistema financiero sea más eficiente, coadyuvará a que la economía se desarrolle favorablemente, potenciando sus fortalezas con un mayor dinamismo en el proceso de intermediación entre los distintos agentes que participan en la toma de decisiones económicas”. Un buen funcionamiento del sector financiero favorece el crecimiento económico y el bienestar. Pero, a su vez, el sistema financiero es sensible a la evolución de la economía real, ya que, se sustenta en la realidad económica subyacente.
Por tanto, un funcionamiento ineficiente incide negativamente en la economía del país ya sea por la disminución del crédito, el incremento de su costo o, en el peor de los casos, por el impacto de hipotéticas quiebras.
Por todo lo anterior, resulta más que justificado el interés y la oportunidad de este trabajo, cuya finalidad es evaluar y medir el nivel de interconectividad de las entidades que componen los bancos múltiples del sistema financiero dominicano para determinar cómo el desbalance en algún sector económico puede afectar la red de bancaria bipartita por medio de una prueba de estrés.
1.4 Alcance
En el presente trabajo, se proponen buenas prácticas para el entendimiento, evaluación y gestión del riesgo sistémico, cuyo detalle cuenta con un alcance que comprende la cartera de créditos y bancos múltiples que hacen parte del sistema financiero dominicano. Cabe anotar, que en dichas entidades hay una alta probabilidad de desencadenarse un evento de riesgo sistémico, generando un efecto de contagio tanto en otras carteras, como hacia la misma entidad que los financió, incidiendo, por ende, en la salud del sistema financiero completo.
2. Revisión de literatura
La mejor evidencia sobre la importancia que tiene la regulación del riesgo sistémico y los efectos adversos sobre la estabilidad financiera es que la literatura sobre los temas de topología de redes y riesgo sistémico ha crecido considerablemente, especialmente a partir de la crisis financiera de 2007-2008.
En República Dominicana, tanto la Superintendencia de Bancos como el Banco Central tienen modelos cuantitativos de alerta temprana que han ido evolucionando en el tiempo. No obstante, la literatura en el tema evoluciona rápidamente a medida que se elaboran nuevas metodologías de análisis de riesgo. Por lo tanto, es importante desarrollar e implementar modelos adecuados que utilicen de forma eficiente y diferente la información disponible, como un modelo que identifique el riesgo sistémico utilizando cuentas del balance general, enfocado en evaluar el riesgo de interconexión de las exposiciones por medio de redes financieras bipartitas, y así poder detectar tempranamente vulnerabilidades que puedan poner en riesgo la salud del sistema financiero dominicano.
Mitchell (1969) define una red como un conjunto particular de interrelaciones entre un conjunto limitado de individuos, con la propiedad adicional de que las características de estas interrelaciones, consideradas como una totalidad, pueden ser utilizadas para interpretar el comportamiento de las partes implicadas. Es factible vincular dicho concepto mediante la Teoría de Grafos. Diestel (2010) expone que la red se constituye por nodos conectados por aristas, donde los nodos son los entes y las aristas, las relaciones que les unen. La representación de la información correspondiente a los patrones de relaciones entre actores se realiza generalmente mediante el uso de grafos, donde un grafo es una representación de un conjunto de objetos en el que los pares de objetos están conectados mediante relaciones entre ellos (Wasserman & Faust, 1994).
El concepto de red tiene múltiples aplicaciones desde el ámbito tecnológico (red de comunicaciones), al ámbito biológico (relaciones entre especies en un ecosistema), al ámbito financiero (red financiera o bancaria) o al ámbito social (relaciones dentro de una red social) (García, 2017).
Papadimitriou, et al. (2013) propone el uso de conceptos de la teoría de redes para identificar entidades que forman parte del núcleo de una red financiera, lo que permite a un supervisor concentrar esfuerzos.
Chan-Lau (2010), plantea recomendaciones sobre la mejor manera de regular las entidades que presentan altas interconexiones y cómo garantizar que se encuentren en el perímetro de la regulación, dado que las instituciones y empresas podrían tener relaciones directas o indirectas entre sí. Las directas podrían corresponder a exposiciones de una empresa hacia otra en sus estados financieros, mientras que las relaciones indirectas hacen referencia a las derivadas de contrataciones entre las compañías. El documento ilustra el uso del análisis de redes (nodos y conexiones en grafos) basado en el balance general para evaluar el riesgo interconectado de las exposiciones directas en los sistemas financiero.
Los modelos de redes financieras permiten capturar aspectos que no pueden ser descritos ni por los enfoques tradicionales centrados en las dimensiones macroeconómicas agregadas ni por aquellos que miran el nivel microeconómico de las empresas de forma aislada (Stiglitz, 2000).
Investigadores y analistas de bancos centrales y de otras instituciones vinculadas con la estabilidad financiera, han llevado adelante una gama de estudios para abordar esta temática en los últimos períodos (Martínez-Jaramillo, et al. 2012, 2014; Battiston, et al. 2013; Huang, et al. 2013; León, et al. 2014).
Uno de los indicadores más representativos como medida de impacto sistémico es DebtRank, introducido por Battiston, et al. (2012), que es una medida de centralidad de la red que incorpora el impacto indirecto de una institución financiera. De Castro & Miranda (2013) modelaron una red conjunta de bancos-empresas y bancos-bancos en Brasil. Con el uso de DebtRank, los autores demostraron que las dificultades financieras procedentes de las empresas pueden propagarse a través de la red interbancaria, afectando los niveles de liquidez.
Las redes bipartitas se caracterizan porque existen dos clases diferenciadas de nodos (actores - películas, aeropuertos - vuelos, bancos – activos, etc.) y las conexiones solo son posibles entre nodos de clases diferentes. Estas redes aparecen con frecuencia en ecología, por ejemplo, para representar las relaciones entre depredadores y presas o parásitos y huéspedes (García, 2017).
Por su parte, Huang, et al. (2013), proponen un método para construir una red bipartita de riesgo sistémico. Su modelo se construyó utilizando series de tiempo de los bancos y sus activos bancarios. Plantean que existe vínculo entre un banco y un activo si el banco tiene el activo en su balance.
Las carteras de activos de los bancos comerciales contienen categorías de activos tales como préstamos comerciales, hipotecarios e inversiones a corto y largo plazo. Se modelan los bancos según cómo construyen sus carteras de activos (figura 1). En su análisis empírico, eligieron los datos de balance de bancos comerciales de Estados Unidos de 2007 y compararon la predicción del modelo de los bancos en quiebra con los bancos en quiebra reales después de 2007. Descubrieron que, el modelo identifica de manera eficiente una parte significativa de los bancos en quiebra reales informados por la Corporación Federal de Seguro de Depósitos. Los resultados sugieren que este modelo podría ser útil para las pruebas de estrés de riesgo sistémico para los sistemas financieros.
Figura 1
Modelo de red bipartita de activos bancarios con bancos como un tipo de nodo y activos como el otro tipo de nodo
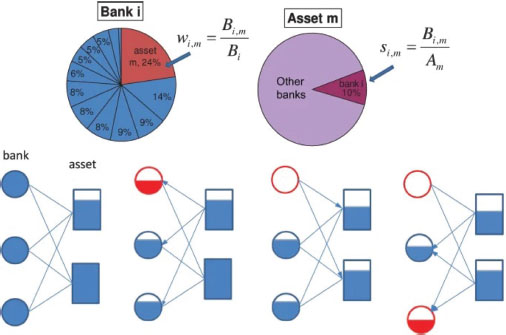
Fuente. Cascading Failures in Bi-partite Graphs: Model for Systemic Risk Propagation, Huang, et al. 2013.
En línea con lo anterior, Sakamoto & Vondeska (2016, 2017), efectuaron un ejercicio similar partiendo de la crisis japonesa a fines de la década de 1990, destacando la importancia de considerar no solo las carteras de activos de los bancos individuales, sino también las conexiones entre los bancos para proteger a las instituciones financieras contra fallas en cascada.
La relación prestamista/prestatario entre bancos y empresas, también fue abordada para el caso japonés, a través de una red de créditos bipartitos (Aoyama, et al. 2013). Este documento presenta escenarios de tensión, que incluyen: i) dificultades financieras en ciertos bancos, contexto en el cual se halla una relación no lineal entre la importancia y el tamaño, y ii) el deterioro en empresas de algunos sectores industriales, que ocasionó impactos en bancos, y empresas de otros sectores económicos.
Del mismo modo, Vodenska, et al. (2021), elaboraron un modelo dinámico de propagación del riesgo utilizando una red bipartita enfocada a la crisis de la deuda soberana europea de 2009-2012. En adición, proponen un indicador de riesgo sistémico simple y dinámico, que mide la cantidad de daño que sufre la red bancaria por la quiebra de un banco en particular. Recomiendan el seguimiento en tiempo real de la acumulación de riesgo en el sistema financiero para mejorar la gestión de riesgos por parte de los bancos centrales, así como de las propias instituciones financieras.
Poledna, et al. (2021), desarrollaron un método para cuantificar el riesgo sistémico derivado de la superposición de carteras en México, en el cual cuantifican el riesgo de las interconexiones indirectas entre entidades financieras, por medio de redes bipartitas. Demuestran que centrarse solo en las exposiciones interbancarias directas subestima los niveles de riesgo sistémico total hasta en un 50% según los supuestos del modelo. Al representar el sistema financiero como una red multicapa de exposiciones interbancarias directas (contagio de incumplimiento) y exposiciones externas indirectas (carteras superpuestas), estiman la influencia mutua de diferentes canales de contagio.
Caccioli et al. (2014), consideran que las tenencias de activos comunes han sido el principal vector de contagio en la crisis financiera de 2008. La representación de un sistema financiero está dada en términos de una red de N bancos y M activos. En su estudio, asumen que cada vez que un banco invierte en un activo, se traza un enlace en la red que conecta ese banco con ese activo. La red resultante es bipartita (figura 2), lo que significa que hay dos grupos de nodos (bancos y activos) y que solo hay enlaces entre estos dos grupos.
Figura 2
Representación gráfica de la red bipartita de bancos y activos. Los bancos se indican con círculos, los activos con cuadrados. Los enlaces conectan a los bancos con los activos que tienen en sus carteras. En este ejemplo N = 4, M = 3, el grado promedio de los bancos es μb=1.5 y el grado promedio de los activos es μa=2
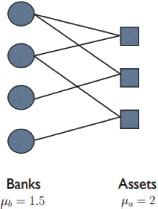
Fuente. Stability analysis of financial contagion due to overlapping portfolios, Caccioli, F. et al. 2014.
La mayor parte de la literatura sobre sistemas de alerta temprana se centra en bancos individuales, ignorando los posibles efectos de red. El dato ideal para medir la fuerza de la conexión es la exposición del banco a otros bancos. Lamentablemente, esta información no está disponible para el público en general, por lo que es necesario utilizar variables proxy para detectar la intensidad de la exposición. La red financiera construida sobre esas variables proxy puede proporcionar información de bancos potencialmente vulnerables a efectos de los distintos sectores económicos a nivel de la cartera de créditos y el riesgo de contagio a otros bancos.
Este estudio está orientado a desarrollar una herramienta que permita analizar la respuesta de un sistema financiero específico frente a situaciones de impacto que se presenten. Y así, ayudar al regulador no solo a identificar las debilidades del sistema, sino también a guiar su respuesta en casos de crisis, incertidumbres o incidencias en los distintos sectores económicos en los que se desenvuelven los deudores que componen la cartera de créditos de las entidades.
3. Metodología utilizada
Se analiza el riesgo sistémico desde un enfoque financiero, haciendo uso de la cartera de créditos -segmentada por sector económico- de los clientes de los bancos múltiples que componen el sistema financiero dominicano. Se hace mediante la estimación del riesgo sistémico a través de la construcción de redes financieras bipartitas y la implementación de una prueba de estrés considerando choques en los sectores económicos más sensibles de la economía dominicana.
3.1 Red financiera bipartita
Distintos investigadores han llevado adelante una gama de estudios para abordar el riesgo sistémico desde un enfoque de redes bipartitas (Cáceres, 2017; Martínez-Jaramillo, et al. 2012; Battiston, et al. 2013; Huang, et al. 2013; León, et al. 2014).
Desde una perspectiva formal, algunos autores (Landaberry, et al. 2021; Yanquen, et al. 2022; Squartini, et al. 2017; Banaccolto, et al. 2017; Das, 2016) coinciden en qué, una red es un grafo G, es decir, un par ordenado (V, E) donde V es un conjunto no vacío, E es una colección disjunta con, y los elementos de E son de la forma {u, v} para u, v ∈ V. Los elementos en V se llaman vértices o nodos, mientras que los elementos en E se llaman aristas. Dada una arista e = {u, v}, se dice que u es adyacente a v (y viceversa), se dice que e une a u y v, y se dice que u y v son conexas. Este trabajo se limitará a gráficos cuyas aristas e no unen ningún vértice consigo mismo, y su conjunto de aristas solo contiene elementos distintos. Este tipo de gráficos se conocen como gráficos simples. En cambio, un gráfico ponderado es un triplete (V, E, W), donde W es una función que asigna un valor numérico (es decir, un “peso”) a cada borde.
Dichos autores destacan que un grafo B = (V, E) es bipartito si su conjunto de vértices V se puede expresar como una unión disjunta V1 ∪ V2, tal que si u, v ∈ Vi, entonces u y v no están unidos por ninguna arista en E para i = 1, 2. La proyección P sobre V1 de un grafo bipartito B = (V1 ∪ V2, E) es el grafo cuyo conjunto de vértices es V1 y e = (u, v) es una arista de P siempre que exista al menos dos aristas e1 = {u, w} y e2 = {v, w} en E con w ∈ V2, es decir, u y v están conectadas en P si comparten al menos un vértice adyacente w ∈ V2.
En el contexto de este trabajo, se emplearán gráficos bipartitos para representar la cartera de créditos que va del conjunto de sectores económicos al conjunto de bancos. Los pesos de cada borde representan la cantidad adeudada.
Las carteras de créditos (más del 50% de los activos financieros) de los bancos múltiples contienen las categorías de los sectores económicos a los que van destinados cada uno de los créditos, estos siguen la clasificación estandarizada propuesta por la Comisión de Estadística de las Naciones Unidas en su Revisión 3.1 (2005), denominadas Clasificación Industrial Internacional Uniforme de todas las Actividades Económicas (CIIU) mostradas en el Anexo 1.
Para cada banco, la cartera de créditos contiene 19 diferentes categorías CIIU, por ejemplo, el banco i tiene su propio balance Bi,0,Bi,1,⋯,Bi,19 para cada categoría correspondiente a los distintos sectores económicos, respectivamente. El total de la cartera de créditos Bi de un banco i es obtenido de la base de datos publicada por la Superintendencia de Bancos. El peso de cada categoría m con respecto del total de la cartera de crédito del banco i es definido como wi,m ≡ Bi,m/Bi . Desde la perspectiva de la participación de cada categoría m de cada banco i, se definió el valor total de la cartera de créditos Bi de todos los bancos i como Am ≡ ∑ Bi,m. Así, la cuota de participación de cada categoría m en cada banco i con respecto del valor total de la cartera de créditos Bi de todos los bancos i es dada por Si,m ≡ Bi,m/Am.
Desde un punto de vista práctico, todos los grafos anteriores se pueden describir en términos de una matriz de peso cuyas entradas indican el peso de un borde que conecta un par de vértices dado. Esta es una matriz W de tamaño N × N, -donde N es la cardinalidad del conjunto de vértices-tal que Wuv > 0 si {u, v} ∈ E y Wuv = 0 en caso contrario. Si se enfoca en las relaciones por pares entre los vértices, se considera la matriz de incidencia, generalmente denotada como I, y sus entradas son 0 o 1. Cada arista incide exactamente en dos vértices, cada columna tiene exactamente dos unos. El número de unos que aparece en cada fila es igual al grado del vértice correspondiente. Una fila compuesta sólo por ceros corresponde a un vértice aislado. Cada elemento de una matriz dada indica la probabilidad de que exista una relación causal entre dos variables (Billio, et al. 2021).
Ejemplo de matriz de incidencia
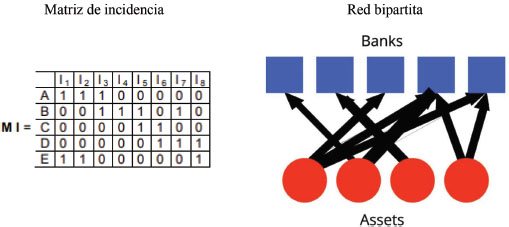
Los gráficos también se pueden visualizar mediante diagramas en los que los vértices están representados por nodos y los bordes por líneas que conectan los nodos asociados con los vértices unidos. Los dígrafos se trazan de manera similar, con la diferencia de que una flecha señala la dirección del arco.
La convención a lo largo del resto del texto será que un arco (u, v) con un peso w será que el prestatario (representados por los sectores económicos en el que desempeñan su actividad económica) u tomó prestados w DOP de la institución v. De esta manera, pretendemos capturar la complejidad de las relaciones crediticias con grafos dirigidos.
3.2 Prueba de Estrés
Las pruebas de estrés han cobrado especial relevancia para evaluar la resistencia de las entidades y sistemas financieros frente a contextos adversos (Cáceres, 2017). En la actualidad, son una herramienta comúnmente utilizada por los reguladores para evaluar la solidez y estabilidad del sistema financiero. Por lo tanto, la realización de una prueba de estrés puede ayudar a identificar los posibles canales de contagio y las vulnerabilidades de la red ante un escenario de estrés extremo, y así permitir a los reguladores y participantes del mercado tomar medidas preventivas para reducir los riesgos sistémicos.
Huang, et al. (2013) mostró el uso de redes financieras bipartitas en una muestra relacionada con los bancos que fallaron durante la crisis financiera (2007-2008), en el que introdujeron un shock en el sistema bancario al reducir el valor de un activo específico y monitorearon el efecto en cascada de esta reducción de valor en los bancos y en otros valores de activos. Concluyeron que el modelo, utilizando datos del balance de 2007 mediante la identificación de los bancos empíricamente en quiebra entre 2008 y 2011, simula bien el proceso de propagación de la crisis e identifica una parte significativa de los bancos en quiebra reales.
En este contexto, la prueba de estrés es utilizada para identificar a las entidades financieras que pudieran promover una crisis financiera, si alguno de los sectores económicos en los que se concentra la mayor parte de su cartera de créditos sufre algún choque.
3.3 Métricas de la red
Las redes bipartitas son una representación útil de las interacciones entre dos conjuntos de entidades, donde las relaciones solo pueden ocurrir entre los conjuntos, pero no dentro de ellos. Las métricas de red son herramientas valiosas para analizar y comprender la estructura y la dinámica de las redes bipartitas.
Las métricas para comparar las redes financieras bipartitas se muestran a continuación:
Densidad de la Red: En las redes bipartitas, los nodos se dividen en dos grupos y la estructura de la red está determinada por las conexiones entre los dos grupos. La medida de densidad es útil para evaluar la cantidad de conexiones que existen entre los dos grupos (Newman, 2010). Es definida como, la relación entre el número de aristas de la red dividido por el número de aristas posibles, donde E es la cantidad de aristas reales y N la cantidad de nodos de la red (Wasserman & Faust, 1994).
Grado de Centralidad: Las medidas de centralidad también son importantes en las redes bipartitas, ya que indican qué nodos en cada grupo son los más importantes en términos de conexiones con el otro grupo (Newman, 2010). El grado di, es el número de aristas de un nodo. Cuanto mayor es la medida de centralidad, mayor es la importancia que tiene un nodo en una red (Martínez, et al. 2014). A mayor grado de centralidad, mayor número de instituciones afectadas. La centralidad de la red es el promedio de grados de nodos normalizados de tal manera que 0 ≤ C ≤ 1.
Conectividad. Mide la tendencia de los nodos a conectarse con otros nodos del mismo grado. Así, los nodos de alto grado tienden a estar conectados entre sí y, en sentido contrario, una red desordenada indica que los nodos de alto grado tienden a estar conectados con nodos de bajo grado (Lavin, et al. 2019). Se calcula utilizando el número de aristas que terminan en el nodo I, ki, E es nuevamente el número de aristas reales de la red, y Wij es la matriz de incidencia. Esta medida captura la tendencia de los nodos a conectarse con nodos que tienen propiedades similares (grado) (Newman, 2002). La conectividad está ligada a -1 ≤ A ≤ 1, cuando A = 1, se dice que la red tiene patrones de mezcla perfecta, cuando A = 0 la red no está conectada, si A = -1 la red es completamente desconectada.
4. Resultados
Para estudiar las propiedades de las entidades, este trabajo se enfocó en la construcción de una red bipartita que conecte los bancos con la cartera de créditos que poseen, lo que permite analizar la interconexión entre ellos, como se muestra a continuación en la Figura 3. La red financiera bipartita se desarrolló utilizando el peso promedio de cada crédito de los bancos, durante los meses del año 2022, de acuerdo a las 19 diferentes categorías CIIU mencionadas con anterioridad. A partir de esta información se construyó una matriz de incidencia que representa la relación entre los bancos y los activos.
Figura 3
Representación gráfica de la red bipartita de bancos y cartera de crédito por sector económico. La red indica la cuota de participación de cada categoría m en cada banco i con respecto del valor total de la cartera de créditos Bi de todos los bancos i es dada por Si,m ≡ Bi,m/Am
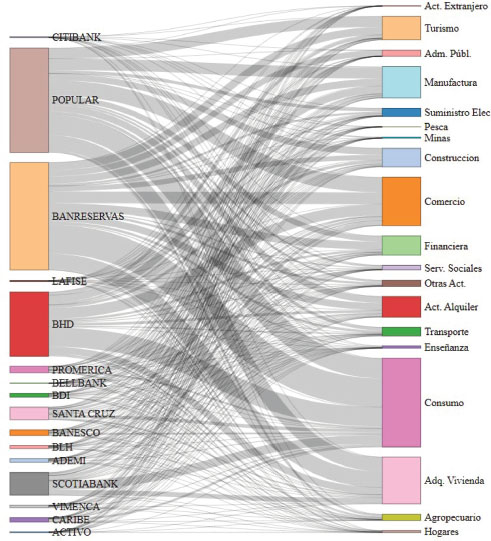
Fuente. Elaboración propia.
Se aplicaron diversas métricas de redes para evaluar la estructura y el comportamiento de la red bipartita. En particular, se calculó la densidad de la red, el grado de centralidad de los nodos y la conectividad entre los nodos. Estas métricas permitieron identificar los nodos más importantes en la red y su nivel de influencia.
Tabla 1
Indicadores de las redes financieras bipartitas
Indicador |
Caso dominicano (2022) |
Colombia3 Préstamos Comerciales entre bancos y firmas (dic-2020) |
Chile Mutual funds and stocks of financial industry (2017) |
European sovereign debt crisis - market data and bank asset holdings (2021) |
EBA-capital-asset pricing model (2009-2015) |
FED emergency loans program to global financial institutions (2008 - 2010) |
Densidad |
0.46 |
0.45 |
0.41 |
- |
0.24 |
- |
Centralidad |
0.65 |
- |
0.62 |
0.60 |
- |
0.40 |
Conectividad |
-0.41 |
- |
-0.23 |
- |
- |
- |
Fuente. Elaboración propia.
Como muestra la tabla anterior, para el caso del coeficiente de conectividad, los resultados obtenidos cercanos a -1 indican que las propiedades o atributos similares que poseen los nodos no tienden a conectarse ente ellos, como son las etiquetas o valores asignados. En otras palabras, los sectores económicos similares con alto volumen de créditos dentro de la cartera tienden a tener menos representación en la cartera de las demás entidades. Similares a los resultados observados en el mercado de inversiones chileno cuando la red bipartita se somete a modelos de robustez, el cual muestra que los fondos con alta dependencia están conectados con fondos de baja influencia.
Por otra parte, con el fin de evaluar la resiliencia de la red ante posibles escenarios de estrés, se realizó una prueba de estrés en la que adoptaron dos escenarios, considerando los sectores económicos con más influencia en la red bipartita y más relevantes para el estudio.
El primer escenario, supuso la caída en default del 20% de la cartera de créditos dirigida a los sectores económicos de agricultura y turismo, el trabajo de Maino & Tintchev (2012) del Fondo Monetario Internacional (FMI), concluye que este porcentaje modela de una manera más realista los shocks a los créditos de los diferentes sectores económicos. Asimismo, el autor Cihak (2007) recomienda la aplicación de diferentes choques a los sectores económicos, dependiendo de los tamaños relativos de las exposiciones crediticias de los bancos a estos sectores y su calibración puede basarse en escenarios históricos.
Por lo anterior, el segundo escenario consideró también los riesgos físicos asociados a los cambios medioambientales a los que está expuesto el territorio dominicano, debido a que se encuentra en una zona expuesta a desastres naturales, como huracanes y sequias, y los efectos permanentes en los patrones del clima, como el aumento del nivel del mar. En los últimos años, los sectores económicos nacionales más impactados por fenómenos atmosféricos han sido el de turismo y el agropecuario, debido a que, luego de un evento climático la infraestructura hotelera se afecta, disminuye la llegada de turistas y la producción agrícola nacional se reduce.
Sin embargo, según los datos publicados por el Banco Central, los ingresos percibidos por estos sectores representan en promedio alrededor del 14.6% del PIB. De tal manera que, estas actividades económicas aportan a la generación de empleos, la entrada de divisas y la producción agroalimentaria del país4.
Consecuentemente, para este segundo escenario se plantea un choque de 50% a la cartera dirigida al sector turismo y de 30% del sector agropecuario. Este último en menor porcentaje, en razón de que, como política para amortiguar el impacto de fenómenos atmosféricos en el sector agropecuario, el gobierno dominicano en 1972 creó el Fondo Especial para Desarrollo Agropecuario (FEDA). Asimismo, los productores agropecuarios del país están respaldados por la Aseguradora Agropecuaria Dominicana (AGRODOSA) ante la ocurrencia de algún evento atmosférico.
Mediante el cálculo del Índice de Solvencia, requerido en el Reglamento de Normas Prudenciales de Adecuación Patrimonial aprobado por la Tercera Resolución de Junta Monetaria de fecha 30 de marzo del 2004, considerando los dos escenarios mencionados anteriormente, con corte a diciembre de 2022, se demostró que un choque en el capital requerido por la caída en default de la cartera de créditos de dos de los sectores económicos más interconectados en la red bipartita, específicamente los sectores de agricultura y turismo, caerían por debajo del mínimo regulatorio (10%), bajo el escenario de estrés más extremo, el Banco de Reservas y el Banco López de Haro. No obstante, en el primer escenario sugerido el índice de solvencia permanece en valores superiores a los requeridos.
La Tabla 2 compara los escenarios de choque al patrimonio técnico de los bancos múltiples, considerando el escenario descrito en el papel de trabajo de Maino & Tintchev (2012) y el escenario basado en el tamaño relativo de las exposiciones crediticias de los bancos a estos sectores y los escenarios históricos presentados con anterioridad (Cihak, 2007).
5. Conclusión
La construcción de una red bipartita que conecte los bancos con la cartera de crédito, por sector económico, permite evaluar la estructura y el comportamiento de la red financiera. La aplicación de métricas de redes (densidad, centralidad y conectividad) y pruebas de estrés arrojaron información valiosa para la identificación de posibles riesgos y vulnerabilidades. En consecuencia, la elaboración de una red bipartita puede ser una herramienta útil para la evaluación y monitoreo de la estabilidad financiera. Es importante para los hacedores de políticas y regulaciones en el sector financiero considerar los riesgos asociados de fenómenos atmosféricos, a través de escenarios prospectivos que tomen en cuenta los sectores de la economía que pudieran verse más afectados, y así evitar o controlar cualquier contagio al sector financiero o la economía en general.
Tabla 2
Cálculo del índice de solvencia estresado
Diciembre de 2022 (Valores en Millones de RD$) |
||||||||
Entidad |
Patrimonio técnico ajustado (Dic-2022) |
Patrimonio técnico ajustado (Primer Escenario Estresado) |
Patrimonio técnico ajustado (Segundo Escenario Estresado) |
Activos y contingentes ponderados por riesgo de crédito y mercado |
Mínimo regulatorio |
Índice de solvencia (Dic-2022) |
Índice de solvencia (Primer Escenario Estresado) |
Índice de solvencia (Segundo Escenario Estresado) |
ADEMI |
2,930.0 |
2,580.4 |
2,303.6 |
15,615.0 |
10% |
18.8% |
16.5% |
14.8% |
BANESCO |
3,574.7 |
3,384.1 |
3,132.7 |
27,085.1 |
10% |
13.2% |
12.5% |
11.6% |
BANRESERVAS |
61,491.5 |
53,837.3 |
43,454.2 |
447,593.0 |
10% |
13.7% |
12.0% |
9.7% |
BDI |
2,835.8 |
2,761.5 |
2,678.1 |
15,456.0 |
10% |
18.3% |
17.9% |
17.3% |
BHD |
56,094.1 |
51,863.5 |
46,802.1 |
341,556.6 |
10% |
16.4% |
15.2% |
13.7% |
BLH |
1,630.0 |
1,468.7 |
1,237.8 |
12,658.5 |
10% |
12.9% |
11.6% |
9.8% |
CARIBE |
2,691.7 |
2,604.0 |
2,510.1 |
19,427.3 |
10% |
13.9% |
13.4% |
12.9% |
CITIBANK |
2,698.4 |
2,698.4 |
2,698.4 |
13,768.1 |
10% |
19.6% |
19.6% |
19.6% |
LAFISE |
1,402.9 |
1,382.0 |
1,366.7 |
9,031.1 |
10% |
15.5% |
15.3% |
15.1% |
POPULAR |
80,588.0 |
70,341.7 |
56,684.8 |
511,324.8 |
10% |
15.8% |
13.8% |
11.1% |
PROMERICA |
3,551.0 |
3,468.7 |
3,383.4 |
30,449.9 |
10% |
11.7% |
11.4% |
11.1% |
SANTA CRUZ |
11,030.3 |
10,677.1 |
10,289.6 |
75,570.3 |
10% |
14.6% |
14.1% |
13.6% |
SCOTIABANK |
22,974.4 |
22,021.2 |
20,929.1 |
139,530.5 |
10% |
16.5% |
15.8% |
15.0% |
VIMENCA |
2,283.6 |
2,283.6 |
2,283.6 |
11,409.8 |
10% |
20.0% |
20.0% |
20.0% |
Fuente. Elaboración propia.
Futuros trabajos podrían ser elaborados usando otros sectores económicos (en lugar de los sectores turismo y agropecuario) y probar con otras entidades de intermediación financiera o incluso otro tipo de activos en la red.
6. Bibliográfica consultada y citada en el texto
Aldasoro, I., Gatti, D., Faia, E., (2016). “Bank networks: contagion, systemic risk and prudential policy”. BIS Working Papers No. 597. Bank for International Settlements. https://www.bis.org/publ/work597.pdf
Aoyama, H., Battiston, S., Fujiwara, Y., (2013). “DebtRank Analysis of the Japanese Credit Network”. Kyoto University and Research Institute of Economy, Trade and Industry. https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=51c7f4412b5a64c1b89c33e2835082943421afe9
Battiston, S., Caldarelli, G., Pirotte, H., Bersini, H., Roukny, T., (2013). “Default Cascades in Complex Networks: Topology and Systemic Risk”. Scientific Reports. http://dx.doi.org/10.1038/srep02759
Battiston, S., Tasca, P., Kaushik, R., Caldarelli, G., (2012). “DebtRank: Too Central to Fail? Financial Networks, the FED and Systemic Risk”. Scientific Reports. https://doi.org/10.1038/srep00541
Billio, M., Casarin, R., Costola, M., Iacopini, M., (2021). “COVID-19 spreading in financial networks: A semiparametric matrix regression model”. Econometrics and Statistics. https://doi.org/10.1016/j.ecosta.2021.10.003
Bonaccolto, G., Caporin, M., Panzica, R., (2017). “Estimation and Model-Based Combination of Causality Networks”. SAFE Working Paper No. 165. http://dx.doi.org/10.2139/ssrn.2909585
Caccioli, F., Shrestha, M., Moore, C., Farmer, J. D., (2014). “Stability analysis of financial contagion due to overlapping portfolios”. Journal of Banking & Finance. Pages 233-245. https://doi.org/10.1016/j.jbankfin.2014.05.021
Cáceres, J., (2017). “Riesgo de contagio en el sistema financiero boliviano – Análisis a través de redes de pagos interbancarios y del financiamiento de operaciones de crédito a empresas”. Revista de Análisis, Volumen N° 27, pp. 91-118. Banco Central de Bolivia. https://www.bcb.gob.bo/webdocs/publicacionesbcb/revista_analisis/ra_vol27/articulo_4_v27.pdf
Cadavid, L., (2019). “Medición del Riesgo Sistémico Intra-bancario”. Universidad EAFIT. https://repository.eafit.edu.co/handle/10784/16060
Chan-Lau, J., (2010). “Balance Sheet Network Analysis of Too-Connected-ToFail Risk in Global and Domestic Banking Systems”. SSRN Electronic Journal. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1566442
Chavarría, E., (2014). “Redes Bancarias y Riesgo Sistémico: Desarrollo de un Algoritmo de Análisis y Diagnóstico”. Universidad de Chile. https://repositorio.uchile.cl/handle/2250/130258
Cihak, M., (2007). “Introduction to Applied Stress Testing”. IMF Working Paper WP/07/59. https://www.imf.org/external/pubs/ft/wp/2007/wp0759.pdf
Das, S., (2016). “Matrix Metrics: Network-Based Systemic Risk Scoring”. The Journal of Alternative Investments. https://srdas.github.io/Papers/JAI_Das_issue.pdf
De Castro, R., Miranda, B., (2013). “Contagion Risk within Firm-Bank Bivariate Networks”. Banco Central de Brasil. Working Papers No. 322, p. 1-60. https://www.bcb.gov.br/pec/wps/ingl/wps322.pdf
Diestel, R., (2010). “Graph Theory: 4th ed”. University of Hamburg. https://link.springer.com/10.1007/978-3-642-14279-6
Garcia, J., (2017). “Representación gráfica de redes bipartitas basada en descomposicion k-core”. Universidad Politécnica de Madrid. https://oa.upm.es/49329/
Gómez, J., Hirs, J., Sanin, S., (2018). “Dynamic relations between oil and stock markets: Volatility spillovers, networks and causality”. Borradores de Economía No. 1051. Banco de la República de Colombia. https://repositorio.banrep.gov.co/bitstream/handle/20.500.12134/9389/be_1051.pdf
Huang, X., Vodenska, I., Havlin, S., Stanley, H., (2013). “Cascading Failures in Bi-partite Graphs: Model for Systemic Risk Propagation”. Sci Rep 3, 1219. Nature Scientific Reports. https://doi.org/10.1038/srep01219
Landaberry, V., Caccioli, F., Rodriguez, A., Baron, A., Martinez, S., Lluberas, R., (2021). “The contribution of the intra-firm exposures network to systemic risk”. Latin American Journal of Central Banking. https://doi.org/10.1016/j.latcb.2021.100032
Lavin, J., Valle, M., Magner, N., (2019). “Modeling Overlapped Mutual Funds’ Portfolios: A Bipartite Network Approach”. Volume 2019, Article ID 1565698, 20 Pages. Complexity. https://doi.org/10.1155/2019/1565698
León, C., Berndsen, R., (2014). “Rethinking financial stability: Challenges arising from financial networks’ modular scale-free architecture”. Journal of Financial Stability. http://dx.doi.org/10.1016/j.jfs.2014.10.006
Maino, R., Tintchev, K., (2012). “From Stress to Costress: Stress Testing Interconnected Banking Systems”. IMF Working Papers. https://www.imf.org/en/Publications/WP/Issues/2016/12/31/From-Stress-to-Costress-Stress-Testing-Interconnected-Banking-Systems-25734
Martinez-Jaramillo, S., Alexandrova-Kabadjova, B., Bravo-Benitez, B., Solorzano-Margain, J., (2012). “An Empirical Study of the Mexican Banking System’s Network and Its Implications for Systemic Risk”. Bank of México. Working Paper 2012-07. http://dx.doi.org/10.2139/ssrn.2140144
Martinez-Jaramillo, S., Alexandrova-Kabadjova, B., Bravo-Benitez, B., Solorzano-Margain, J., (2014). “An Empirical Study of the Mexican Banking System’s Network and Its Implications for Systemic Risk”. Article. Journal of Economic Dynamics and Control Volume 40, Pages 242-265. https://doi.org/10.1016/j.jedc.2014.01.009
Mitchell, J.C., (1969). “The Concept and Use of Social Networks”. In J. C. Mitchell (Ed), SocialNetworks in Urban Situations. Manchester, UK: Manchester University Press.
Naciones Unidas, Departamento de Estadísticas Económicas (2005). “Clasificación Industrial Internacional Uniforme de todas las Actividades Económicas (CIIU)”. Rev. 3.1. https://unstats.un.org/unsd/classifications/Econ/Download/In%20Text/ISIC31_Spanish.pdf
Newman, M. E. J., (2002). “Assortative Mixing in Networks”. American Physical Society Vol. 89, No. 4, pp. 208-701. https://doi.org/10.1103/PhysRevLett.89.208701
Newman, M. E. J., (2010). “Networks: An Introduction”. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199206650.001.0001
Papadimitriou, T., Gogas, P., Tabak, B., (2013). “Complex networks and banking systems supervision”. Physica A: Statistical Mechanics and its Applications. Volume 392, Issue 19, 1 October 2013, Pages 4429-4434. Science Direct. https://doi.org/10.1016/j.physa.2013.05.013
Poledna, S., Martínez-Jaramillo, S., Caccioli, F., Thurner, S., (2021). “Quantification of systemic risk from overlapping portfolios in the financial system”. Volume 52. Journal of Financial Stability. https://doi.org/10.1016/j.jfs.2020.100808
Sakamoto, Y., Vodenska, I., (2016). “Systemic risk and structural changes in a bipartite bank network: a new perspective on the Japanese banking crisis of the 1990s”. Journal of Complex Networks, Volume 5, Issue 2, June 2017, Pages 315–333. https://doi.org/10.1093/comnet/cnw018
Sakamoto, Y., Vodenska, I., (2017). Erratum to “Systemic risk and structural changes in a bipartite bank network: a new perspective on the Japanese banking crisis of the 1990s”. Journal of Complex Networks, Volume 5, Issue 3, July 2017, Page 512. The Journal of Alternative Investments. https://doi.org/10.1093/comnet/cnx012
Santana, M., (2015). “El sistema financiero de la República Dominicana: Evaluación de su eficiencia y productividad mediante el Análisis Envolvente de Datos (DEA)”. Universidad de Valencia. https://roderic.uv.es/handle/10550/50617
Squartini, T., Almog, A., Caldarelli, G., Lelyveld, I., Garlaschelli, D., Cimini, G., (2017). “Enhanced capital-asset pricing model for bipartite financial networks reconstruction”. Phys. Rev. E 96, 032315. American Physical Society. https://link.aps.org/doi/10.1103/PhysRevE.96.032315
Stiglitz, J., (2000). “La economía del sector público, 3ra edición”. Columbia University Press. https://desarrollomedellin.files.wordpress.com/2018/08/stiglitz-2000-tercera-edicion.pdf
Vodenska, I., Dehmamy, N., Becker, A., Buldyrev, S., Havlin, S., (2021). “Systemic stress test model for shared portfolio networks”. Nature Scientific Reports. https://doi.org/10.1038%2Fs41598-021-82904-y
Wasserman, S., Faust, K., (1994). “Social Network Analysis: Methods and Applications”. New York: Cambridge University Press. https://doi.org/10.1525/ae.1997.24.1.219
Yanquen, E., Livan, G., Montañez, R., Martínez, S., (2022). “Measuring systemic risk for bank credit networks: A multilayer approach”. Latin American Journal of Central Banking. http://dx.doi.org/10.1016/j.latcb.2022.100049
7. Anexos
Anexo 1. Clasificación Industrial Internacional Uniforme de todas las Actividades Económicas (CIIU)
CLASIFICACIÓN INDUSTRIAL INTERNACIONAL UNIFORME DE TODAS LAS ACTIVIDADES ECONÓMICAS (CIIU) - REVISIÓN 3.1 |
A - Agricultura, Ganadería, Caza Y Silvicultura |
B – Pesca |
C - Explotación De Minas Y Canteras |
D - Industria Manufacturera |
E - Suministro De Electricidad, Gas, Vapor Y Aire Acondicionado |
F – Construcción |
G - Comercio Al Por Mayor Y Al Por Menor; Reparación De Los Vehículos De Motor Y De Las Motocicletas |
H - Alojamiento Y Servicios De Comida |
I - Transporte Y Almacenamiento |
J - Actividades Financieras Y De Seguro |
K - Actividades Inmobiliarias, Alquiler Y Actividades Empresariales |
L - Administración Pública Y Defensa: Planes De Seguridad Social De Afiliación Obligatoria |
M – Enseñanza |
N - Servicios Sociales Y Relacionados Con La Salud Humana |
O - Otras Actividades De Servicios Comunitarios, Sociales Y Personales |
P - Actividades De Los Hogares En Calidad De Empleadores, Actividades Indiferenciadas De Producción De Bienes Y Servicios De Los Hogares Para Uso Propio |
Q - Actividades De Organizaciones Y Órganos Extraterritoriales |
Y - Consumo De Bienes Y Servicios |
Z - Compra Y Remodelación De Viviendas |
Anexo 2. Matriz de incidencia de la red financiera bipartita
|
ACTIVO |
ADEMI |
BANCAMERICA |
BANESCO |
BANRESERVAS |
BDI |
BELLBANK |
BHD |
BLH |
CARIBE |
CITIBANK |
LAFISE |
POPULAR |
PROGRESO |
PROMERICA |
SANTA CRUZ |
SCOTIABANK |
VIMENCA |
A |
0.0001 |
0.1298 |
0.0025 |
0.0211 |
0.6759 |
0.0092 |
0.0021 |
0.4957 |
0.0023 |
0.0116 |
0.0031 |
0.0023 |
0.6591 |
0.0841 |
0.0078 |
0.0409 |
0.0761 |
0.0019 |
B |
0.0000 |
0.0014 |
0.0000 |
0.0002 |
0.0024 |
0.0000 |
0.0000 |
0.0070 |
0.0000 |
0.0001 |
0.0000 |
0.0000 |
0.0062 |
0.0001 |
0.0000 |
0.0000 |
0.0000 |
0.0000 |
C |
0.0000 |
0.0030 |
0.0036 |
0.0028 |
0.0538 |
0.0027 |
0.0005 |
0.0717 |
0.0005 |
0.0021 |
0.0013 |
0.0077 |
0.0606 |
0.0066 |
0.0081 |
0.0029 |
0.0248 |
0.0004 |
D |
0.0008 |
0.0512 |
0.0096 |
0.1145 |
1.7746 |
0.0677 |
0.0029 |
1.7593 |
0.0434 |
0.0188 |
0.1814 |
0.0168 |
3.2046 |
0.0965 |
0.1022 |
0.2263 |
0.4683 |
0.0267 |
E |
0.0000 |
0.0085 |
0.0002 |
0.0617 |
1.0777 |
0.0129 |
0.0001 |
0.6043 |
0.0026 |
0.0060 |
0.1746 |
0.0099 |
0.8163 |
0.0622 |
0.0106 |
0.0391 |
0.1531 |
0.0096 |
F |
0.0012 |
0.0503 |
0.0326 |
0.1203 |
2.8680 |
0.1965 |
0.0064 |
1.1529 |
0.1480 |
0.0625 |
0.0026 |
0.0228 |
1.1563 |
0.1061 |
0.1148 |
0.1460 |
0.1870 |
0.0553 |
G |
0.0068 |
0.3654 |
0.0248 |
0.1916 |
3.1372 |
0.1490 |
0.0072 |
2.8735 |
0.0699 |
0.0551 |
0.2200 |
0.0507 |
5.6051 |
0.3658 |
0.1847 |
0.5252 |
0.9759 |
0.0481 |
H |
0.0006 |
0.0435 |
0.0019 |
0.0701 |
1.5329 |
0.0141 |
0.0004 |
0.9371 |
0.0269 |
0.0229 |
0.0054 |
0.0022 |
2.6994 |
0.0973 |
0.0142 |
0.0452 |
0.0919 |
0.0051 |
I |
0.0006 |
0.0713 |
0.0065 |
0.0413 |
0.4733 |
0.0416 |
0.0032 |
0.3998 |
0.0212 |
0.0152 |
0.0299 |
0.0050 |
0.8378 |
0.0654 |
0.0191 |
0.0861 |
0.1026 |
0.0053 |
J |
0.0006 |
0.0227 |
0.0150 |
0.0679 |
1.9918 |
0.0343 |
0.0029 |
0.3079 |
0.0123 |
0.0271 |
0.0069 |
0.0227 |
1.2598 |
0.1181 |
0.0277 |
0.1261 |
0.1518 |
0.0143 |
K |
0.0037 |
0.0884 |
0.0250 |
0.1432 |
1.9696 |
0.2102 |
0.0034 |
0.7486 |
0.1471 |
0.0590 |
0.0190 |
0.0248 |
1.6129 |
0.2091 |
0.1277 |
0.1348 |
0.1227 |
0.0362 |
L |
0.0000 |
0.0018 |
0.0001 |
0.0187 |
4.8253 |
0.0009 |
0.0002 |
0.0039 |
0.0015 |
0.0011 |
0.0000 |
0.0025 |
0.0208 |
0.0005 |
0.0001 |
0.0008 |
0.0017 |
0.0004 |
M |
0.0001 |
0.0093 |
0.0017 |
0.0027 |
0.1142 |
0.0223 |
0.0001 |
0.1301 |
0.0256 |
0.0083 |
0.0000 |
0.0049 |
0.2320 |
0.0053 |
0.0047 |
0.0227 |
0.0210 |
0.0064 |
N |
0.0000 |
0.0169 |
0.0040 |
0.0068 |
0.2243 |
0.0085 |
0.0001 |
0.2399 |
0.0112 |
0.0062 |
0.0002 |
0.0052 |
0.4758 |
0.0102 |
0.0081 |
0.0338 |
0.0269 |
0.0049 |
O |
0.0009 |
0.0478 |
0.0099 |
0.0235 |
0.8417 |
0.0268 |
0.0008 |
0.3746 |
0.0067 |
0.0132 |
0.0000 |
0.0018 |
0.5310 |
0.0557 |
0.0207 |
0.0469 |
0.1183 |
0.0055 |
P |
0.0004 |
0.0533 |
0.0010 |
0.0094 |
0.0222 |
0.0047 |
0.0016 |
0.5064 |
0.0307 |
0.0179 |
0.0000 |
0.0092 |
0.0573 |
0.0001 |
0.0073 |
0.0376 |
0.0058 |
0.0043 |
Q |
0.0000 |
0.0003 |
0.0012 |
0.0059 |
0.0682 |
0.0000 |
0.0000 |
0.0026 |
0.0005 |
0.0050 |
0.0032 |
0.0007 |
0.0515 |
0.0002 |
0.0002 |
0.1159 |
0.0016 |
0.0008 |
Y |
0.0326 |
0.2777 |
0.0829 |
0.3652 |
6.5088 |
0.1142 |
0.0175 |
5.0584 |
0.1102 |
0.7501 |
0.0035 |
0.0210 |
6.1458 |
0.8045 |
0.5049 |
0.7706 |
2.4340 |
0.1521 |
Z |
0.0070 |
0.0927 |
0.0224 |
0.1847 |
4.2153 |
0.1294 |
0.0033 |
1.9673 |
0.2023 |
0.0768 |
0.0000 |
0.0091 |
4.5512 |
0.1815 |
0.0232 |
0.2648 |
1.3789 |
0.0801 |
_______________________________
3 Superintendencia Financiera de Colombia (SFC). Los créditos comerciales representaron el 75.6% del total de la cartera a diciembre de 2020. Gómez, J. et al. 2018.
4 Informe de Estabilidad Financiera del Banco Central de la República Dominicana (2021).
