Pruebas no paramétricas para determinar la aleatoriedad de los datos en procesos productivos y procedimientos para calcular estadísticas en pareja

Introducción

La Investigación de Operaciones consiste en un conjunto de técnicas que contribuyen a la solución de problemas de una amplia gama de actividades, mediante la aplicación de diversas técnicas sustentadas en modelos matemáticos y estadísticos. Es el caso, principalmente, de los métodos paramétricos —estadístico Z, t-student, F, entre otros—, de los métodos no paramétricos —prueba de signo, pruebas de suma de rangos, Kolmogórov-Smirnov, entre otros— y de las técnicas de análisis multivariante —análisis factorial, análisis de clúster, análisis discriminante, entre otras—. A su vez, la utilización de alguno de los estadísticos señalados implica, primero, la comprobación del cumplimiento de supuestos, como la determinación de la aleatoriedad de los datos (Anderson, Sweeney & Williams 2016b; Hillier & Lieberman 2015; Taha 2017).

Ahora bien, las pruebas no paramétricas de corridas de datos se aplican con el fin de identificar tendencias, irregularidades y agrupaciones en los datos, cuyos resultados señalan si un determinado proceso —por ejemplo, productivo empresarial— está bajo control; esto es, si únicamente causas comunes de variación inherentes al proceso —causas no especiales— afectan la salida de dicho proceso. Por lo tanto, un patrón normal para un proceso bajo control es uno que garantiza la aleatoriedad de los datos de las muestras observadas (Levin, Rubin, Rastogi & Hussain, 2014; Robbins, 2015).

En este sentido, la aplicación de las pruebas corridas de datos pretende garantizar la robustez de los análisis estadísticos, más aún cuando en las organizaciones se dedica tiempo y recursos para ello, razón por la cual es deseable llegar a conclusiones correctas. Por ejemplo, cuando se necesita establecer si las diferencias observadas entre las muestras de los datos estudiados son resultado del azar o si efectivamente sus poblaciones correspondientes son diferentes. Así también, otro ejemplo, si se comparan dos o más medias muestrales con la prueba t-student y ANOVA, la presencia de un valor de la varianza significativamente diferente puede ocultar diferencias entre las medias y llevar a conclusiones incorrectas. Además, en este estudio se presentan también casos en los cuales se aplican procedimientos para calcular estadísticas en pareja, destacándose la prueba de promedio de pareja, diferencias de pareja y pendientes en pareja (Correa, Iral & Rojas, 2006; Lind, 2012b).

Dicho lo anterior, los objetivos de esta investigación de caso son, por un lado, verificar la aleatoriedad en muestras de datos y, por el otro, aplicar procedimientos para calcular estadísticas en pareja en procesos manufactureros de la empresa Creaciones MFN, de la ciudad de Ambato, utilizando el software Minitab. Las hipótesis que se contrastan en este estudio, para la prueba de corridas no paramétrica son:

− H₀ : El orden de los datos es aleatorio en las muestras observadas, por lo tanto, el proceso está bajo control. − H₁ : El orden de los datos no es aleatorio en las muestras observadas, por lo tanto, el proceso no está bajo control.

A continuación, se detalla el estado del arte y la práctica, se establecen los métodos y aplicación, se presentan los resultados, la discusión y conclusiones.

1. Estado del arte y la práctica

El muestreo es un procedimiento o técnica para determinar las características de una población a partir de la información de la muestra. Es considerada una técnica estadística aplicable en las encuestas y experimentos. Es el núcleo central de la estadística inferencial. Se aplica para estimar el valor de un parámetro de la población y para probar alguna aseveración —o hipótesis— acerca de una población. Siendo los errores más comunes con respecto al muestreo, por un lado, sacar conclusiones muy generales a partir de la observación de solo una parte de la población, se denomina error de muestreo y, por otro, sacar conclusiones aplicadas a una población mucho más grande de la que originalmente se tomó la muestra o error de Inferencia (Flores-Tapia & Flores-Cevallos, 2017; Triola, 2018).

Los tipos de muestreo pueden ser probabilístico y no probabilístico; en el primero, todos los individuos tienen la misma probabilidad de ser elegidos para formar parte de la muestra, asegurándose la representatividad de la muestra extraída mientras que, el segundo, se utiliza cuando es imposible o muy difícil obtener la muestra por métodos aleatorios o probabilísticos, o cuando se quiere mostrar que existe un determinado rasgo en la población (Levin et al., 2014).

Señalado lo anterior, la aleatoriedad de los datos es un supuesto utilizado en algunas pruebas estadísticas para determinar si existen causas comunes de variación en un proceso o causas que surgen fuera del sistema estudiado, por cuanto únicamente las variaciones inherentes al proceso —causas comunes— no afectan sus salidas y está bajo control el proceso. En este sentido, se han desarrollado algunas pruebas para determinar la aleatoriedad de los datos, denominadas pruebas de corridas, de carácter no paramétrico porque no se expresa un supuesto sobre los parámetros de distribución de la población y se utiliza para determinar si el orden de respuestas arriba o debajo de un valor especificado o si el orden de respuestas con respecto a la media es aleatorio; siendo una corrida un conjunto de observaciones consecutivas inferiores o superiores a un valor señalado (Minitab, 2020).

Por otra parte, entre las pruebas de procedimientos para calcular estadísticas en pareja se destacan promedios en pareja, diferencias en pareja y pendientes en pareja (Eppen, Gould, Schmidt, Moore & Weattherford, 2000; Gujaratí & Porter, 2010). Estas pruebas son utilizadas con pruebas no paramétricas e intervalos de confianza, por ejemplo, Wilcoxon, Mann Whitney y estimados robustos de pendiente, respectivamente. A continuación, se detallan cada una de ellas

1.1. Prueba de promedios en pareja

La primera aplicación, promedio en pareja, es la más extensa, pero la menos notoria. Se la conoce también como promedios de Walsh. Calcula y almacena las medias de cada par posible de valores de un conjunto de datos, incluyendo el emparejamiento de cada valor consigo mismo. Por ejemplo, el conjunto de datos {1, 3} tiene tres pares: 1 pareado consigo mismo, 1 pareado con 3 y 3 pareado consigo mismo, siendo los promedios en parejas las medias de estos pares. Por lo tanto, este conjunto de datos tiene tres promedios en parejas: 1, 2 y 3. Además cabe señalar que los promedios en parejas se utilizan con el método de Wilcoxon (Minitab, 2020). Las ecuaciones (1) y (2) aplicadas en la solución de esta prueba se indican a continuación.

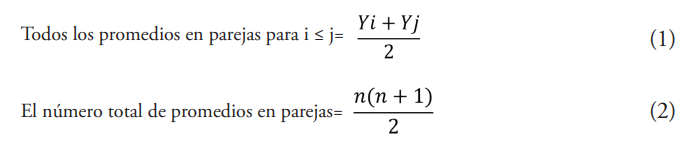
Donde:

Yi: iésimo valor del conjunto de datos.

Yj: jésimo valor del conjunto de datos.

n: tamaño de muestra.

Por su parte, para estimar la mediana se supone que W₍₁₎ < W₍₂₎ < ... < W_(M), denota los valores ordenados de los promedios en parejas, donde M = n(n+1) /2. Si M es impar, la mediana estimada es el valor del medio. Si M es par, la mediana estimada es el promedio de los dos valores del medio. Es necesario señalar que el estadístico de Wilcoxon es el número de promedios en parejas que son mayores que la mediana hipotética, más la mitad del número de promedios en parejas que son iguales a la mediana hipotética. El estadístico de Wilcoxon se denota como W y el software Minitab obtiene el estadístico de prueba utilizando un algoritmo basado en Johnson y Mizoguchi (1978). Se puede afirmar también que el estadístico de prueba de Wilcoxon es la suma de los rangos asociados con las observaciones que exceden la mediana hipotética.

Para muestras grandes, la distribución de W es aproximadamente normal (3) con una media de 0 y una desviación estándar de 1, N (0,1). Específicamente:

El software Minitab utiliza una corrección de continuidad de 0.5 para el valor p de la aproximación a la normal para las tres hipótesis alternativas (4), (5) y (6), planteadas a continuación.

Donde:

n: el número observado de puntos de los datos después de que se omiten las observaciones que son iguales al valor de la mediana hipotética.

W: el estadístico de prueba de Wilcoxon.

w: el número de promedios de Walsh que exceden la mediana hipotética, más la mitad del número de promedios de Walsh, que son iguales a la mediana hipotética (7), siendo:

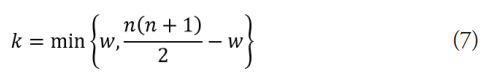
1.2. Prueba de diferencias en pareja

La opción diferencias en pareja calcula y almacena las diferencias entre todos los posibles pares de valores formados en dos columnas. Estas diferencias son muy útiles para pruebas no paramétricos e intervalos de confianza, por ejemplo, el estimado de puntos dados por Mann Whitney se puede calcular como la mediana de las diferencias. Cuando se obtienen dos columnas de datos numéricos, se dice que al instante se obtienen datos faltantes, por lo cual las diferencias en parejas incluyen los valores faltantes (Minitab, 2020).

Esta prueba, en ocasiones, es necesaria para comprobar si un determinado estadístico es aplicable, una vez se haya comprobado primero el supuesto de datos aleatorios, tal como por ejemplo en el caso de Gauss, Student y Fisher, entre otros (Lind, 2012b).

1.3. Prueba de pendientes en pareja

La función pendiente en pareja calcula y almacena la pendiente entre todos los posibles pares de puntos, donde una fila en las columnas y = x define un punto en el plano. Este procedimiento en útil para hallar estimados robustos de la pendiente de una línea a través de los datos. Se utiliza cuando se tiene dos columnas de los datos numéricos, una que contenga la variable de respuesta (Y) y una que contenga la variable predictora (X). Pero si se obtienen dos faltantes o la pendiente no esta definida, es decir, la pendiente de una línea paralela al eje y, la pendiente se almacenará como faltante (Anderson, Sweeney & Williams 2016a).

Por otra parte, para las pruebas de corridas y las pruebas de procedimientos para calcular estadísticas en pareja se cuenta con herramientas de software para ayudar a los analistas en la implementación de modelos computarizados, tales como el software Minitab, SPSS, R, GNA en Java, NIST y Matlab, principalmente (Gujarati & Porter, 2009; IBM, 2020; Microsoft, 2020; Taha, 2017).

Ahora bien, entre los estudios relacionados con la aplicación de técnicas estadísticas y de Investigación de Operaciones que requieren previamente para su aplicación la verificación del supuesto de aleatoriedad de los datos muestrales y otros en los cuales se aplican las pruebas de procedimientos para calcular estadísticas en pareja, se destaca Pino (2019), quien presenta la implementación de un prototipo de aleatoriedad verificable en el sorteo de vocales de mesa, donde la verificación pueda hacerse sin necesidad de asistir físicamente al sorteo o acceder a documentos físicos. Para lograr esto, se usa el servicio público de aleatoriedad verificable del CLCERT, y se contacta con el SERVEL y la junta electoral de Macul para obtener asistencia y retroalimentación.

Así también, Sanz y Espinoza (2017) realizan una aproximación a las periodicidades en los valores pluviométricos de las tres regiones más septentrionales de Chile, esto es, XV, I y II: Arica y Parinacota; Tarapacá y Antofagasta, respectivamente y, luego de sometidos los datos a un rellenado de las series faltantes, se determinan los componentes no aleatorios con test de verificación de aleatoriedad tipo; constatándose que, lejos de una tendencia, excesivamente general, se destacan las repeticiones a los 3, 5, 8-9, 13 y 22 años que se cotejarán con los posibles mecanismos de producción de lluvia ya establecidos.

Otros autores, Solís et al. (2017), combinan la esteganografía sobre imágenes digitales en formato PNG y en modo de color RGBA de 32 bits, utilizando la técnica del Bit Menos Significativo —LSB, con un generador de bits seudoaleatorio, implementado en base a un autómata celular bidimensional que genera secuencias de bits con apariencia de aleatoriedad, evaluando las secuencias de bits generados mediante las pruebas estadísticas de relación de señal a ruido de pico— PSNR y la entropía relativa de la estegoimagen.

Por su parte, Flores-Tapia, Flores-Cevallos, Mendoza y Valdivieso (2017) investigan el efecto que tiene el tamaño del tallo, las variedades de rosas más importantes cultivables y el estado del botón sobre el volumen total de ventas en la empresa florícola del cantón Latacunga “High Connection Flowers”; utilizan herramientas de los métodos cuantitativos para la toma de decisiones. Esto es, el diseño de experimentos mediante modelos factoriales completos, necesitándose para su aplicación, primero, la contrastación de la hipótesis de igualdad de varianzas y verificación de la aleatoriedad de los datos. 

Por su parte, Parra et al. (2019) presentan la simulación de Montecarlo para dos horas de servicio en la cafetería principal “Lunchscool” de la sede principal de la Universidad Santo Tomás, a partir de la toma de datos se verifica la independencia y uniformidad de los números aleatorios utilizados, finalmente algunos indicadores muestran el tiempo de servicio, el tiempo de llegada, tiempos de espera, tiempos ociosos promedio y factor de ocupación, verificándose que los números aleatorios son uniformes e independientes.

Finalmente, se destaca el trabajo de Cruz (2017), quien, mediante la prueba del coeficiente de reparto, determina el método más apropiado para administrar un medicamento para reducir el sobrepeso, estudiando la lixiviación de los relaves de flotación de cobre y cobalto y determinando las condiciones óptimas de lixiviación, así como los parámetros de funcionamiento más influyentes. Se trata de un diseño factorial, previamente contrasta la hipótesis de aleatoriedad de los datos y de igualdad de varianzas antes de proceder con la prueba ANOVA y así determinar la relación entre las condiciones experimentales y los niveles de rendimiento y define la importancia de los parámetros en los rendimientos de lixiviación. 

No obstante, en los estudios antes referidos no se utiliza un procedimiento metodológico aplicando estos dos tipos de pruebas no paramétricas — aleatoriedad de los datos muestrales y estadísticas en parejas— en muestras tomadas de varios procesos productivos en un mismo estudio de caso, como se realiza en la presente investigación.

2. Métodos y aplicación

El estudio contempla técnicas no paramétricos —una prueba de hipótesis que no requiere que la distribución de la población siga una distribución normal— como son las pruebas de corridas y las pruebas de promedios en parejas, diferencias en parejas y pendientes de pareja que se ajustan a la metodología de Investigación de Operaciones (Flores-Tapia et al., 2017; Hernández-Sampieri, Fernández y Baptista, 2007; Hillier y Lieberman, 2015; Taha, 2017), previéndose seis etapas o fases a seguirse:

− Definición del problema de interés y recolección de datos relevantes.

− Formulación de un modelo matemático que represente el problema.

− Desarrollo de un procedimiento basado en computadora para derivar una solución para el problema a partir del modelo.

− Prueba del modelo y mejoramiento de acuerdo con las necesidades.

− Preparación para la aplicación del modelo prescrito por la administración.

− Implementación.

Cabe señalar, que la metodología cuantitativa es aquella en la que se recogen y analizan datos cuantitativos sobre variables y estudia las propiedades y fenómenos cuantitativos. El alcance del estudio contempla la aplicación de una prueba que permite probar la aleatoriedad de los datos y tres pruebas para calcular estadísticas en pareja, siguiendo tres fases, a saber: definición del problema y recolección de datos, aplicación de los modelos matemáticos y desarrollo del procedimiento basado en computadora (Flores-Tapia & Flores-Cevallos, 2017; Lind, 2012b).

3. Resultados

A continuación, siguiendo la metodología antes indicada, se desarrolla la aplicación y se muestran los resultados de las pruebas de corridas, primero arriba y debajo de la media y, luego, de promedios en parejas, diferencias en parejas y pendientes de pareja consideradas para el caso de estudio, objeto de esta investigación.

3.1. Aplicación de la prueba de corridas arriba y debajo de la media

Antes de proceder con la aplicación de la prueba de corridas arriba y debajo de la media, se establece el enunciado del estudio de caso y las condiciones del mismo, en los siguientes términos:

La empresa MFN (Ecuadornegocios, 2020) inicia sus operaciones en la ciudad de Ambato hace más de diecisiete años; cuenta con dos plantas manufactureras, una, ubicada en el sector los Tres Juanes, y otra, en el parque industrial de Santa Rosa. Esta empresa se dedica a la confección y distribución de prendas de vestir en tejido de punto como camisetas, busos, polos, camisetas tipo BVD, blusas, leggins, ropa para bebé, entre otros, pero su producto principal es la camiseta básica. Para estos productos adquiere regularmente la tela por rollos pesados en kilogramos. A la gerencia le interesa determinar si el peso de los rollos se ajusta a los estándares de variación pactados con el proveedor, pero antes de aquello necesita verificar que los rollos fueron efectivamente seleccionados de manera aleatoria para registrar el peso correspondiente. En una determinada inspección de control de calidad se toman 20 rollos de tela como muestra y sus datos de peso se registran en la tabla 1.

Utilizando el software Minitab se ingresan los datos en la hoja de trabajo y se corre la prueba de corridas arriba y debajo de la media, obteniéndose los siguientes resultados:

Corridas por encima y por debajo de K = 22.353

El número observado de corridas = 9

El número esperado de corridas = 10.6

12 observaciones por encima de K, 8 por debajo

Valor P = 0.443

Por cuanto el valor p resultante (0,443) es mayor que alfa de 0,05, existe suficiente evidencia para concluir que los datos no están en orden aleatorio. Por lo tanto, los rollos de tela no han sido seleccionados de manera aleatoria, consecuentemente el proceso no está controlado y la gerencia tiene que tomar los correctivos —por ejemplo, proceder con una toma de muestra garantizando la aleatoriedad mediante sorteo o el uso de número aleatorios generados por computadora para seleccionar los rollos de tela—.

3.2. Aplicación de la prueba promedios en pareja

La gerencia de la empresa Creaciones MFN está también interesada en conocer si el promedio de volumen de producción diario está dentro de los estándares fijados, para lo cual se toman muestras de cantidades producidas de cada tres de sus productos principales, sabiendo que se aplicará la prueba de Wilcoxon para probar que la mediana de producción es igual o no a la mediana hipotética, esto es si ha cambiado o no con respecto al valor histórico. Los datos muestrales de volúmenes de producción se presentan en la tabla 2.

Asimismo, como se procedió con la prueba de corridas arriba y debajo de la media, utilizando el software Minitab se ingresan los datos en la hoja de trabajo y se corre la prueba de promedios de parejas, obteniéndose los resultados que se presentan a continuación en la tabla 3.

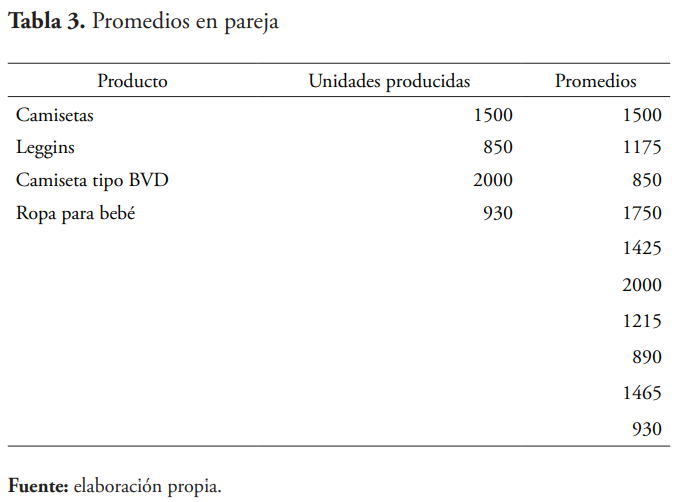
Los resultados obtenidos de la corrida de promedio en parejas muestran el cálculo y almacenamiento del promedio de volumen de producción por cada par posible de valores de los distintos productos manufacturados por esta empresa —camisetas, leggins, camiseta tipo BVD y ropa para bebé—, incluyendo cada valor consigo mismo. Los promedios en parejas calculan y almacenan el promedio para cada par posible de valores en una sola columna, incluyendo cada valor consigo mismo. Estos promedios pueden ser utilizados, por ejemplo, con el método Wilcoxon.

3.3. Aplicación de la prueba diferencias en pareja

La gerencia de la empresa Creaciones MFN está también interesada en conocer cantidades que son producidas, pero no se empacan, con posibles prejuicios para la empresa. Para ello se toman muestras en cada uno de estos procesos, esto es, de cantidades producidas y cantidades empacadas de cuatro de sus productos principales. Los datos muestrales de volúmenes de producción y unidades empacadas durante el mes se muestran en la tabla 4.

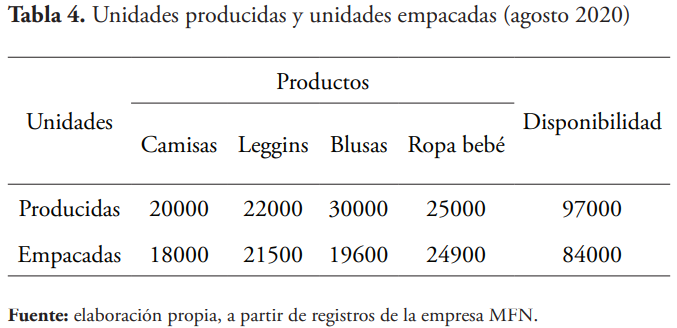
Se procede con el ingreso de los datos correspondientes a Minitab, según la tabla 5.

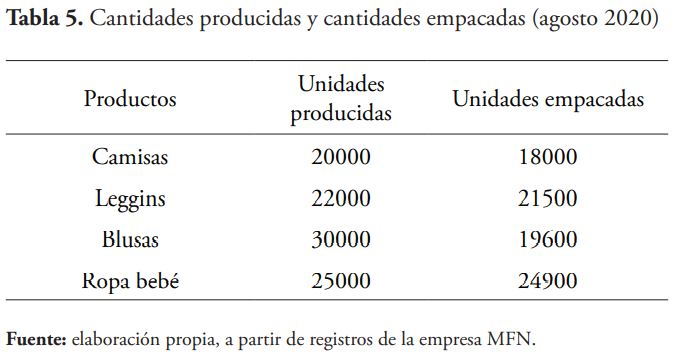
Asimismo, como se procedió con la prueba de corridas promedio en parejas, utilizando el software Minitab se ingresan los datos en la hoja de trabajo y se corre la prueba de diferencias de parejas, obteniéndose los resultados que se presentan a continuación en la tabla 6.

Los resultados obtenidos de la corrida de diferencias en parejas muestran el cálculo y almacenamiento de diferencias entre todos los posibles pares de valores formados por las variables “unidades producidas” y “unidades empacadas”. Esta prueba es útil para pruebas no paramétricas e intervalos de confianza, como es el caso del cálculo del estimado de puntos dado por Mann-Whitney como la mediana de las diferencias, en este caso entre los valores de la variable unidades producidas y la variable unidades empacadas.

3.4. Aplicación de la prueba pendientes en pareja

La gerencia de la empresa Creaciones MFN está también interesada en conocer el volumen de unidades producidas y las cantidades que no se ingresan efectivamente a bodega, con posibles prejuicios para la empresa. Para ello se toman muestras en cada uno de estos procesos, esto es producción e ingreso a bodega, de tres de sus productos principales. Los datos muestrales de volúmenes de producción y unidades ingresadas a bodega durante el mes se muestran en la tabla 7.

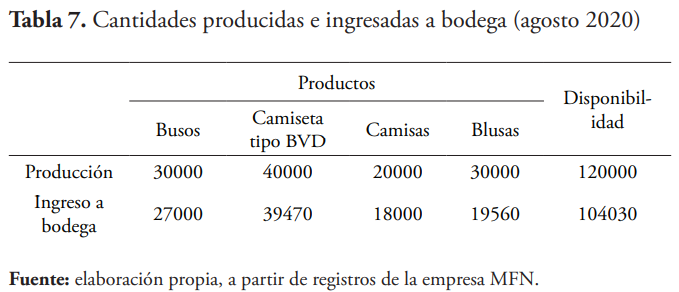
Se procede con el ingreso de los datos correspondientes a Minitab, según la tabla 8.

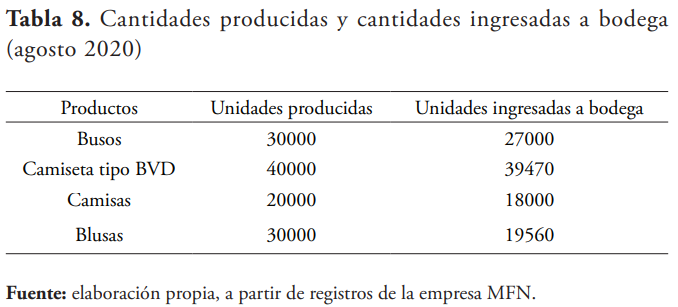
Asimismo, como se procedió con la prueba de promedio en parejas y pendientes en pareja, utilizando el software Minitab se ingresan los datos en la hoja de trabajo y se corre la prueba de pendiente de parejas, obteniéndose los resultados que se presentan a continuación en la tabla 9.

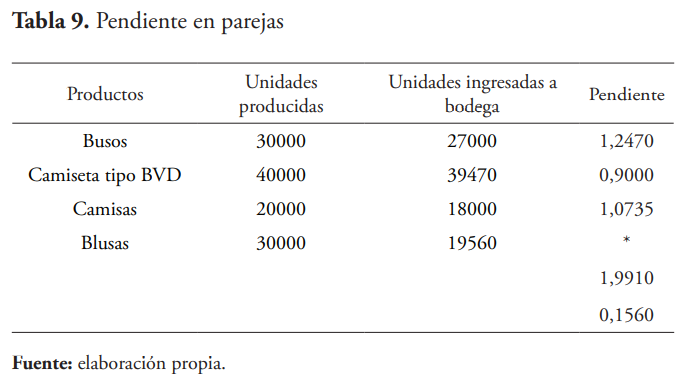
Sabiendo que la pendiente y la intersección definen la relación lineal entre dos variables, se pueden utilizar para estimar una tasa de cambio promedio; de tal manera que, mientras mayor sea la magnitud de la pendiente, más inclinada será la línea y mayor será la tasa de cambio, permitiendo hallar estimados robustos de la pendiente a través de los datos. Los resultados obtenidos de la prueba de diferencias en parejas muestran el cálculo y almacenamiento de la pendiente entre todos los posibles pares de puntos, donde una fila en las columnas y-x define un punto en el plano, en este caso con respecto a las variables unidades producidas y unidades ingresadas a bodega.

4. Discusión y conclusiones

La hipótesis de aleatoriedad de los datos muestrales en el presente caso de estudio ha sido confirmada para los datos estudiados, estableciéndose la posibilidad de aplicación de alguno de los estadísticos que pueden utilizarse con los datos proporcionados por la empresa Creaciones MFN, por ejemplo la prueba t-student para contrastar la medias aritméticas de los pesos de los rollos de tela y si estos se ajustan a un determinado estándar de variación aceptable, que se haya convenido con los proveedores.

Además, se concluye en las pruebas de procedimientos para calcular estadísticas en pareja de este estudio se adaptan con otras pruebas no paramétricas tales como Wilcoxon, Mann-Whitney y robustez de la pendiente de regresión lineal, entre otras. Lo anterior, evidencia que los resultados del estudio son consistentes con la teoría explicada por FloresTapia y Flores-Cevallos (2017); Levin et al. (2014); Lind (2012a); Triola (2018), entre otros.

El artículo verifica que se pueden utilizar las pruebas aplicadas para diversos procesos empresariales. En tal sentido, a lo largo del artículo se ha ido alcanzando los objetivos de esta investigación de caso, esto es, se ha verificado la aleatoriedad en muestras de datos y se han aplicado procedimientos para calcular estadísticas en pareja en procesos manufactureros de la empresa Creaciones MFN, ubicada en la ciudad de Ambato.

Por otra parte, cabe señalar que la aplicación de las pruebas no paramétricas para probar la aleatoriedad de los datos y las pruebas para calcular estadísticas en pareja con el apoyo de herramientas informáticas, como por ejemplo Minitab y otros programas especializados, agilizan los tiempos de procesamiento y ahorran costos significativos para las organizaciones que necesitan información oportuna para la toma de decisiones técnicas, confirmando su utilidad, más aún si las condiciones internas y del entorno empresarial resultan cada vez más complejas, como es el caso de la crisis generada por el COVID-19. No obstante, es necesario recordar que este tipo de técnicas tienen también limitaciones relacionadas con el tipo de muestreo, la recolección de datos, y otros aspectos inherentes al tratamiento estadístico. Lo señalado no significa que su utilidad es cuestionable, por cuanto los tomadores de decisiones empresariales utilizan esta información para diseñar modelos, sistemas y procesos que funcionen bien y contribuyan al logro de los objetivos de la organización.

Agradecimiento

Los autores agradecen la colaboración de la empresa Creaciones MFN por poner a disposición los datos con los cuales se procedió a los cálculos pertinentes. Asimismo, agradecen la traducción al inglés del resumen y revisión final realizada por el Mg. José Conterón, analista de investigación de la PUCESA.