COVID-19 en la República Dominicana: Declaramos la guerra, pero... ¿estamos ganando?

1. Introducción

El riesgo de propagación indiscriminada del COVID-19 es el principal desafío que enfrentan las autoridades gubernamentales, los líderes del sector privado y la ciudadanía en general, a nivel global, incluyendo la República Dominicana, debido a las consecuencias humanitarias y económicas que esto acarrea.

Con el objetivo de analizar la evolución de la pandemia, tanto en términos de su tamaño final y el momento en que alcanza su pico, como de las condiciones bajo las cuales se disipa, hacedores de política e investigadores en todas partes del mundo emplean modelos que les permitan caracterizarla.

Este documento contribuye a esa discusión proponiendo una adecuación al modelo canónico usado en epidemiología (SIR), adaptando el enfoque de estado-espacio usado regularmente en el ámbito de las proyecciones econométricas. Esto, en sí mismo, no es una novedad en términos metodológicos (Sebastian & Victor, 2017) y (Eksin et al., 2019), pero sí lo es en cuanto a su aplicación, dado que se emplea para diagnosticar la dinámica del COVID-19 en la República Dominicana, contrastándola con la de una selección de países.

Evaluando la tendencia del número básico de reproducción (R₀ ) del virus, esto es, la cantidad de contagios adicionales que provoca un infectado nuevo, se concluye que tanto en la República Dominicana como en los países evaluados, las políticas de distanciamiento han reducido la propagación del virus. En el caso dominicano, estas pasaron de un promedio de nueve contagios secundarios, previo a la adopción de las medidas, a un número de dos, posterior a estas.

Las decisiones que adopten las autoridades en las próximas semanas, así como la conducta de la población en general, determinarán si el R0 continuará su ritmo decreciente, resultando en un menor número de vidas afectadas, o revertirá su tendencia.

Las estimaciones hechas al 16 de abril de 2020 sugieren que, de continuar su tendencia decreciente, si se estabilizara alrededor del valor de uno (1) durante los próximos 30 días, como ha ocurrido en China y Corea del Sur, el máximo nivel de contagios rondaría los 13,500, en tanto el mayor nivel de nuevos infectados semanales sucedería hacia finales de abril, alcanzando un tope cercano a los 1,700 casos.

Si por el contrario, se quiebra la tendencia y R₀ se estabiliza en los niveles actuales, la pandemia se propagaría lo suficiente para infectar a alrededor del 7 % de la población dominicana, en tanto el máximo nivel de contagios semanales ocurriría hacia septiembre de 2020 y nos aproximaríamos a los 51,000 casos, lo que evidencia la necesidad de extender y fortalecer las políticas de distanciamiento social.

El resto del documento se organiza como sigue: en la sección 2 se presenta el marco metodológico propuesto, especificando la representación estado-espacio en el modelo epidemiológico SIR. En la sección 3 se analizan los datos utilizados; en tanto, en la sección 4 se presentan los resultados. Finalmente, en la sección 5 se concluye.

2. Metodología

Para caracterizar la evolución de la epidemia ocuparemos el modelo canónico usado en epidemiología (Kermack & McKendrick, 1927), aplicado para el estudio de la evolución del COVID-19 en República Dominicana por De Peña & Ramírez (2020), mejor conocido como SIR. Bajo este marco, la población (N) en riesgo de contraer una enfermedad contagiosa se divide en tres grupos: susceptibles (S_t ), infectados (I^t ) y removidos (R_t ).

Los susceptibles son personas no inmunes al virus, que aún no han entrado en contacto con infectados, pero se contagian al hacerlo. Los infectados son ex-susceptibles que habiendo interactuado con contagiados contrajeron el virus y, por tanto, son capaces de transmitirlo. Los removidos son ex-infectados que contrajeron el virus pero no son capaces de transmitirlo, ya sea porque adquirieron inmunidad tras recuperarse o fallecieron a causa de este.

Por simplicidad, el modelo no considera crecimiento poblacional (i.e.: N = S_t +I _t +R_t ); supone que el período de incubación del agente infeccioso es instantáneo (i.e.: los síntomas se manifiestan a partir del contagio) y asume que el período de contagio es igual al de la duración de la enfermedad (i.e.: los contagiados pueden transmitirlo hasta tanto se recuperen).

Bajo estos supuestos, la dinámica del modelo suele ilustrarse con el siguiente esquema (véase figura 1), que muestra que los susceptibles transicionan al grupo de infectados según la velocidad de contagio de la enfermedad, capturada por el parámetro β; en tanto, los infectados transicionan al grupo de removidos según la duración de la enfermedad, reflejada en el parámetro γ.

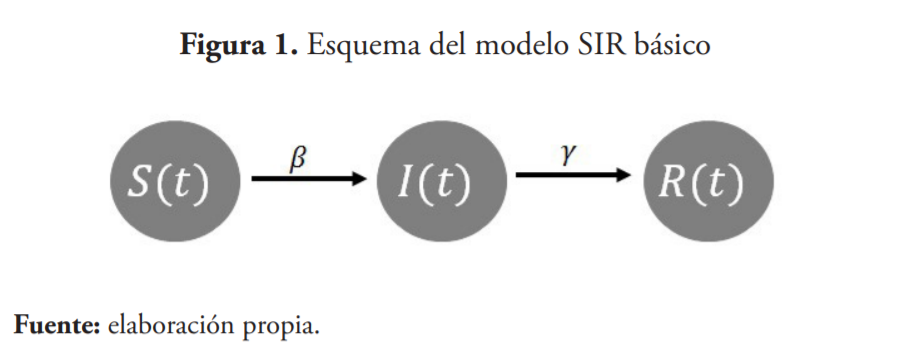
Estas dinámicas se pueden representar a través del siguiente sistema de ecuaciones diferenciales representado:

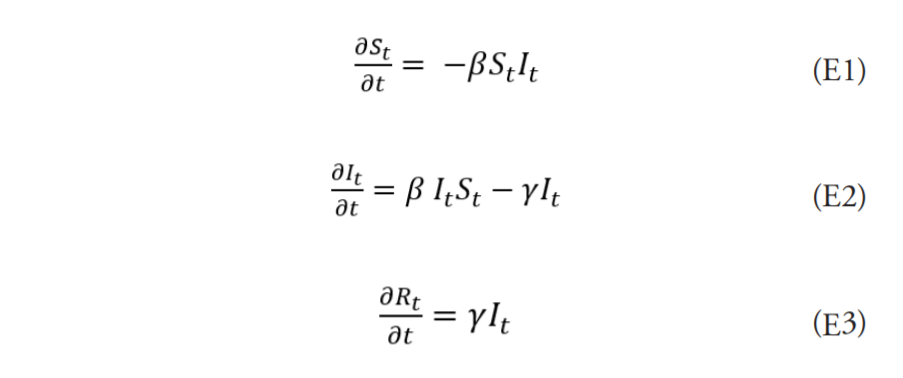
donde β se refiere a la tasa efectiva de contacto, definida como la probabilidad de que el contacto entre un individuo susceptible y un infectado resulte en contagio, en tanto γ corresponde a la tasa de crecimiento de la población removida¹ .

La ecuación 1 muestra que, asumiendo que todos los individuos tienen la misma probabilidad de contagiarse² , la variación del número de susceptibles es inversa a la tasa efectiva de contacto. En la ecuación 2 se observa que la variación del número de infectados aumenta con la cantidad de susceptibles que se contagian (βS tIt ) y decrece en la medida que son removidos (−λI t ). Finalmente, la ecuación 3 captura los infectados que pasan a ser removidos y dejan de incidir en el desarrollo de la epidemia, ya sea porque se recuperaron y adquirieron inmunidad o porque fallecieron.

Una vez definidas las condiciones iniciales del modelo³ más los parámetros β y γ, podremos cuantificar el número de susceptibles, infectados y removidos en cada momento del tiempo, lo que permitirá caracterizar la epidemia en términos de su tamaño final⁴ , el momento en que alcanza su pico y bajo cuáles condiciones se disipa. Nótese que podemos reescribir (E2) en términos de la tasa de crecimiento de los infectados ( $\frac{{\displaystyle \frac{a{i}_t}{at}}}{i_t}=(bs-y)$)y así establecer que la epidemia se disipará (i.e.: $\frac{a{i}_t}{a_t}\le 0$) siempre que $\frac{bs}{y}<1$, y se expandirá en caso contrario. En epidemiología, esta última expresión se conoce como número básico de reproducción ($R_0=\frac{BS}{Y}$ ), y refleja el número promedio de contagios secundarios generados por un caso de contagio nuevo en una población susceptible, durante un período infeccioso (Dietz, 1993).

R₀ es la variable más importante de calcular y monitorear durante un brote infeccioso. Recoge tres elementos fundamentales de la evolución de una epidemia: la duración del contagio, el grado de transmisibilidad de la enfermedad y la tasa de contacto entre sujetos de la población susceptible. Dado que las dos primeras son características inherentes al patógeno, los esfuerzos de las autoridades para mitigar la propagación del virus suelen enfocarse en alterar patrones de contacto entre individuos implementando medidas de distanciamiento social, como toques de queda o cierres de escuelas y negocios⁵ . Esto último implica que la tasa efectiva de contacto, β, en lugar de ser constante, podría variar en el tiempo (β_t ) producto de las intervenciones de las autoridades y, en consecuencia, también R₀ ⁶ .

Partiendo de lo anterior, para capturar de forma más precisa la dinámica de las epidemias ante episodios de intervenciones que alteren la conducta social de los individuos, emplearemos R_t o el número efectivo de reproducción. Liu et al. (2018) señalan que, ante estimaciones confiables de γ, el análisis Bayesiano de β_t y R_t se constituye como una herramienta útil a la hora de analizar la dinámica de las pandemias.

2.1. Modelo espacio-estado

El modelo espacio-estado se especifica usando la ecuación dinámica de los infectados (I(t)), (ecuación E2) en tiempo discreto del modelo SIR presentado y, a diferencia de este modelo, se trata como variable de estado a la tasa de contagio (β_t ), es decir, un parámetro cambiante. La especificación es la siguiente: 

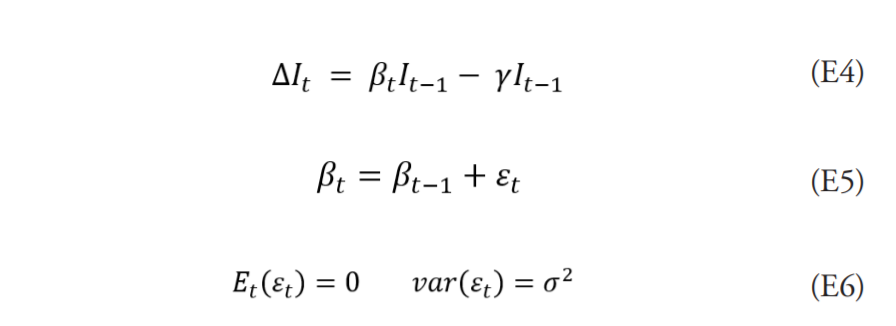
donde la primera expresión es la ecuación de observación, la cual asume que no hay error de medición. Mientras que la segunda es la ecuación de estado que caracteriza la dinámica de la tasa de contagio. El supuesto de que βt es un parámetro cambiante permite una especificación más flexible del modelo SIR y considera el hecho de que este es incidido por la probabilidad de contagio y la interacción humana. Este último factor es impactado por el efecto de las políticas de distanciamiento y otras medidas que limitan la exposición al virus.

3.Datos

Para llevar a cabo la estrategia descrita en la sección anterior se utilizan tres fuentes de datos. La primera de ellas es el número diario de infectados, tanto los acumulados (véase figura 2) como los nuevos (véase figura 3), obtenidos de la base de datos de la web del Centro de Ciencias de Sistemas e Ingeniería de la Universidad Johns Hopkins⁷ . Estas series se utilizan para estimar la tasa de contagio y a partir de los parámetros de transmisión para República Dominicana y un conjunto de países.

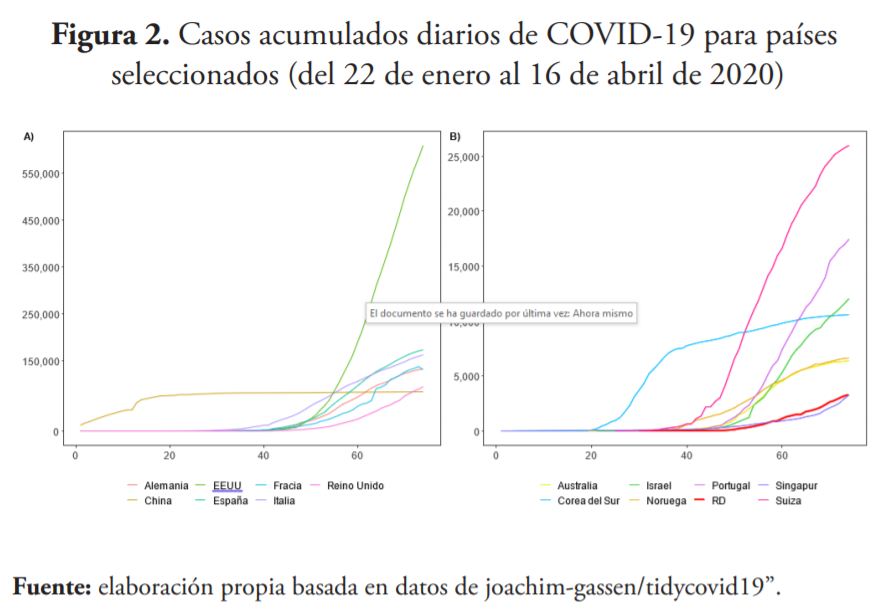
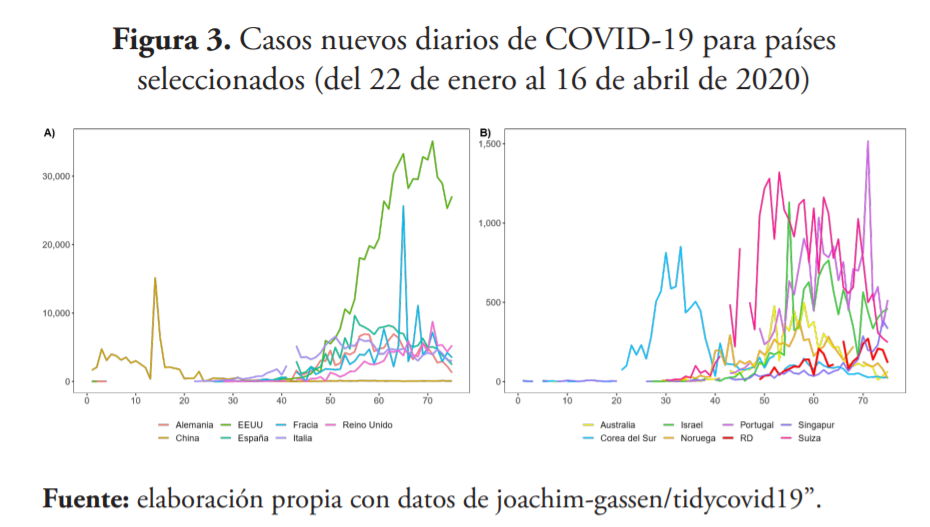
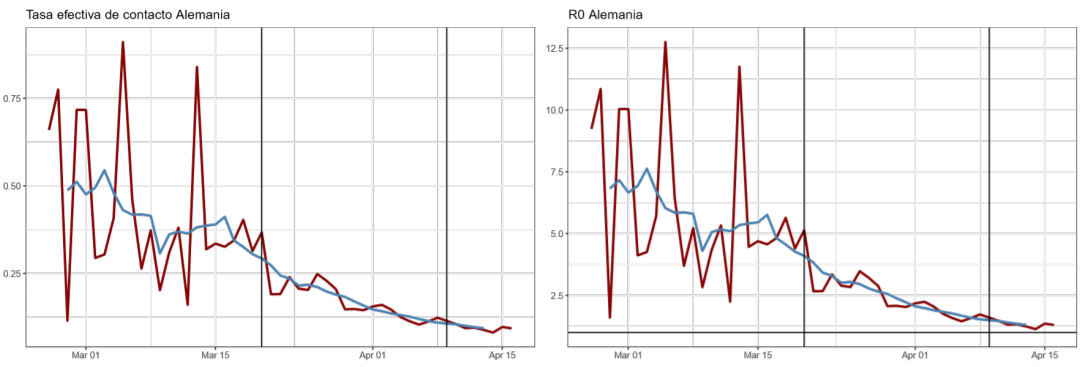
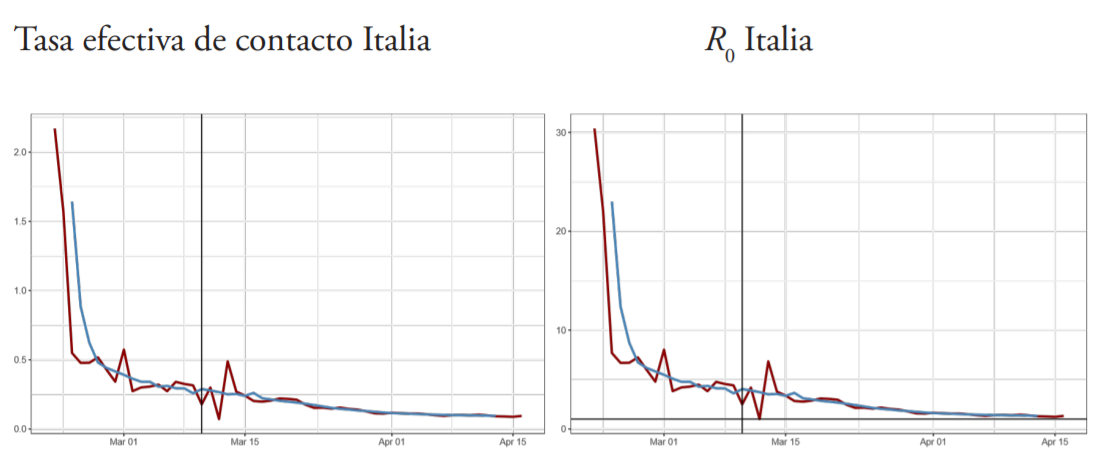
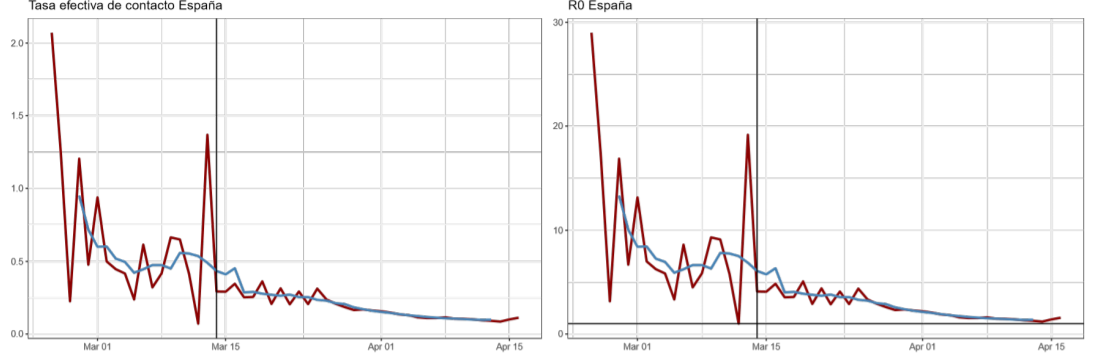
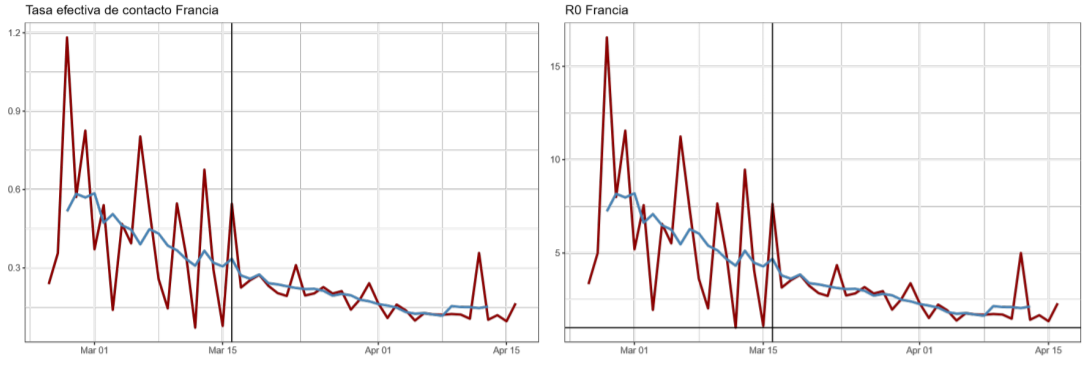
China y Corea del Sur son seleccionados debido a que se encuentran en una fase avanzada de la curva, mientras que Alemania, España, Francia e Italia, a la fecha de la publicación de este documento, se encontraban en la etapa intermedia, cerca de lo que sería un punto de inflexión. Por su parte, Estados Unidos es el caso de un país donde el virus se encuentra en el momento crítico de propagación. La selección de los restantes obedece, al igual que los anteriores, a que se constituyen como los países líderes en realización de pruebas a sus habitantes, garantizando una mejor caracterización de la evolución de la pandemia.

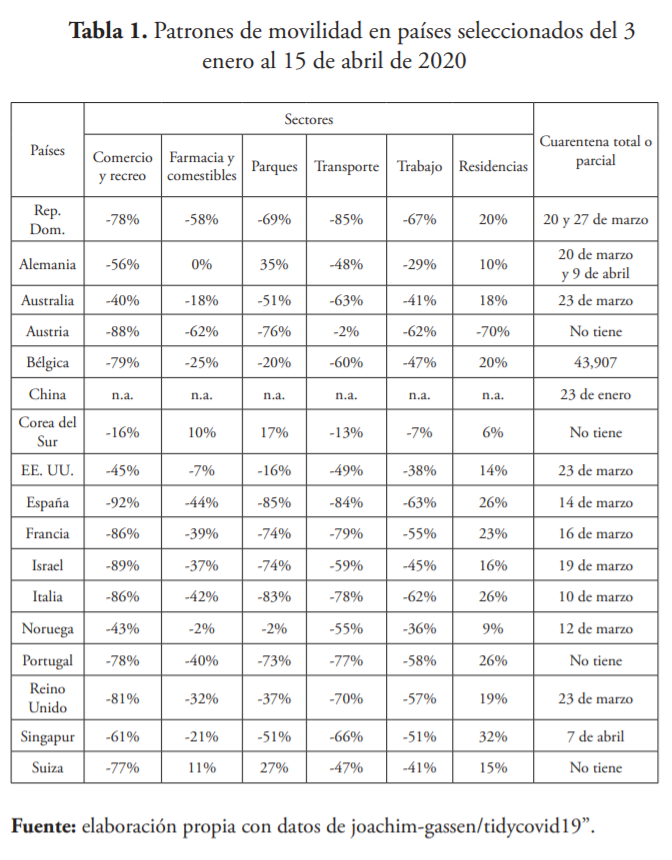
La segunda fuente es la base de datos desarrollada por Joachim Gassem⁸ para el estudio de la pandemia, de la cual se extraen datos de patrones de movilidad publicados por Google. En la tabla 1 se resume esta información para los países en cuestión. La tercera fuente corresponde a las publicaciones oficiales de fechas en las que se adoptaron medidas de restricción de circulación, ya sean parciales o totales, en los países seleccionados.

Por último, las condiciones iniciales del modelo asumen una población N = 10 millones de personas, una tasa de recuperación γ = 1/149 y un primer infectado al 1ro de marzo de 2020. Los valores de los parámetros βt se establecen utilizando la metodología descrita en la sección 2.1. La simulación se ejecuta hasta el 31 de diciembre de 2020.

4. Resultados

Utilizando los datos de contagios por COVID-19 en la República Dominicana y en un grupo de países seleccionados¹⁰, se estiman las tasas efectivas de contacto (β_t ) y el correspondiente número de contagios secundarios (R_t ), con el fin de evaluar la efectividad de las políticas de distanciamiento social a la hora de mitigar la propagación del virus.

En la figura 4 se muestra la evolución de β_t y R_t en la República Dominicana a partir de la detección del primer contagio y, adicionalmente, se presentan datos de la variación de visitas en lugares comúnmente frecuentados por la población¹¹. 

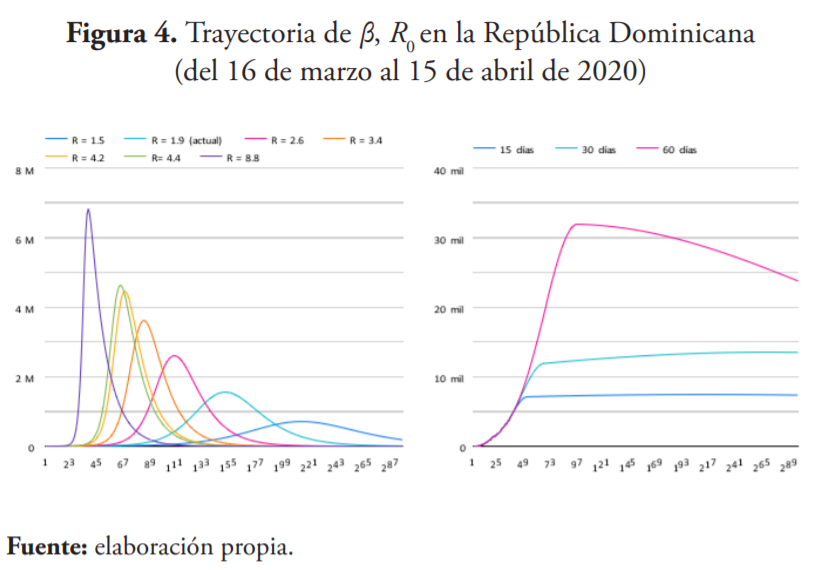
Los resultados reflejan una tendencia decreciente de la tasa efectiva de contacto y, por consiguiente, del grado de propagación del virus. Dicha dinámica se aprecia aún previo a la adopción de medidas gubernamentales, posiblemente reflejando conductas de autoaislamiento adoptadas por las personas, lo que se acentúa a partir de la implementación de las diversas políticas de distanciamiento aplicadas por las autoridades.

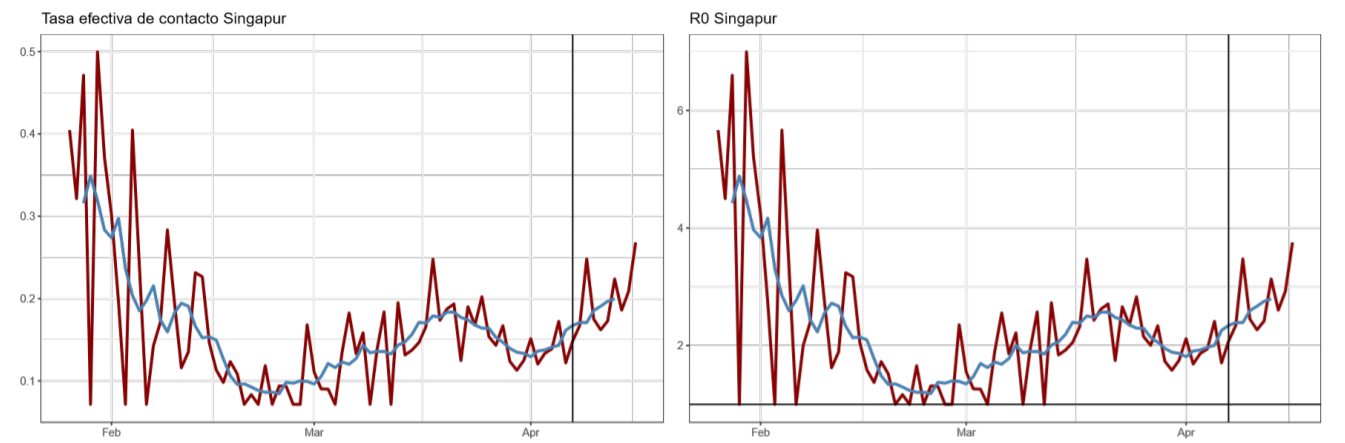
En el caso de República Dominicana, la reducción en la tasa de contacto alcanza el 77 %, consistente con la caída observada en los datos de movilidad de Google (véase tabla 1) y superando los declives observados en Estados Unidos, Francia y Singapur, lo que permitió reducir el promedio de contagios secundarios por semana de un máximo de nueve contagios, previo a la implementación de las medidas, a dos contagios, posterior a dicha implementación.

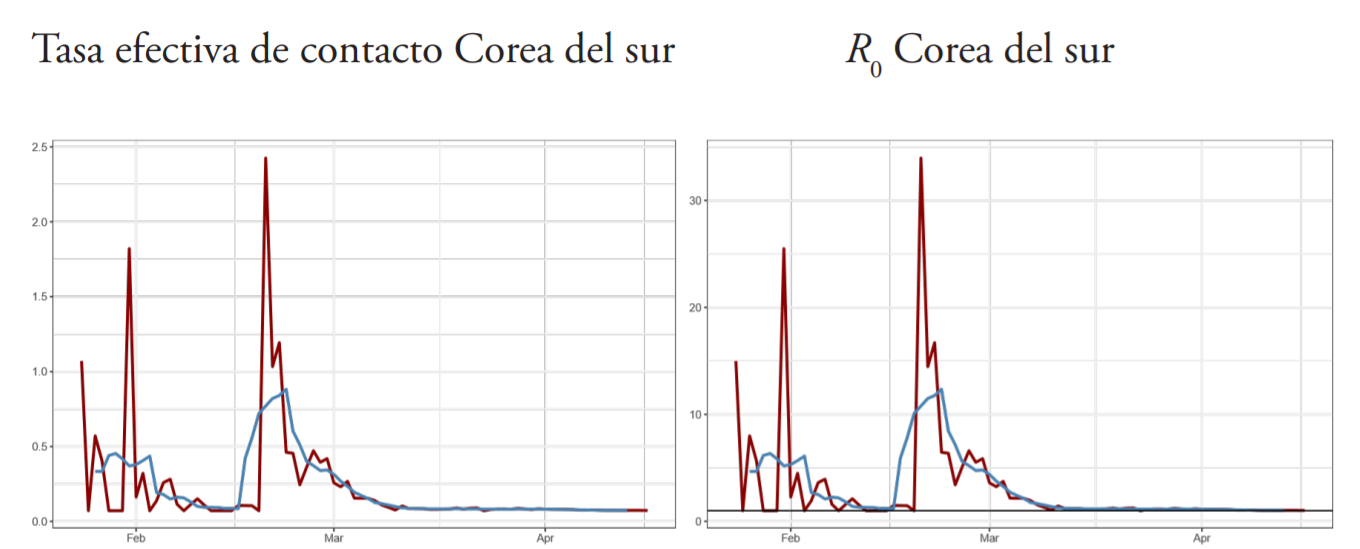
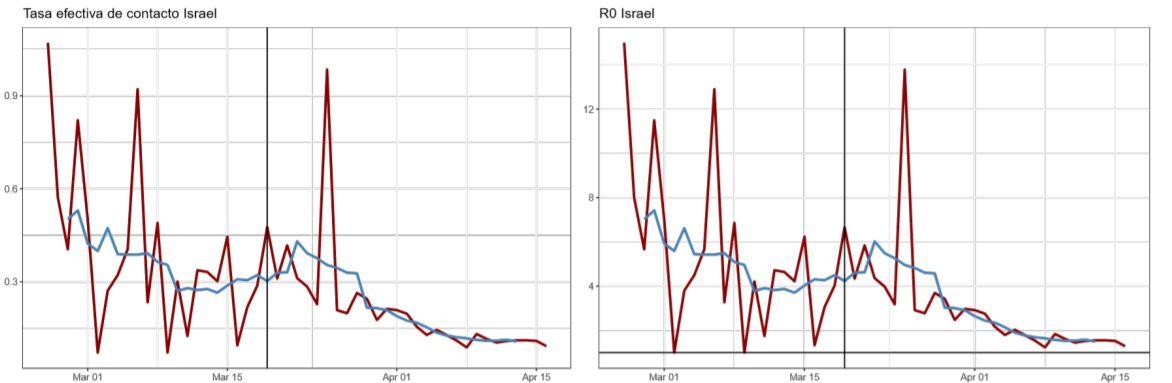
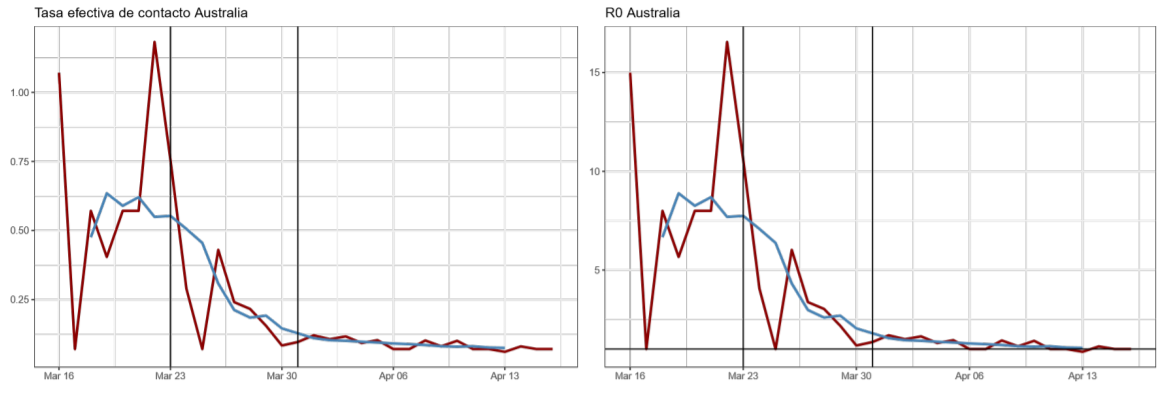
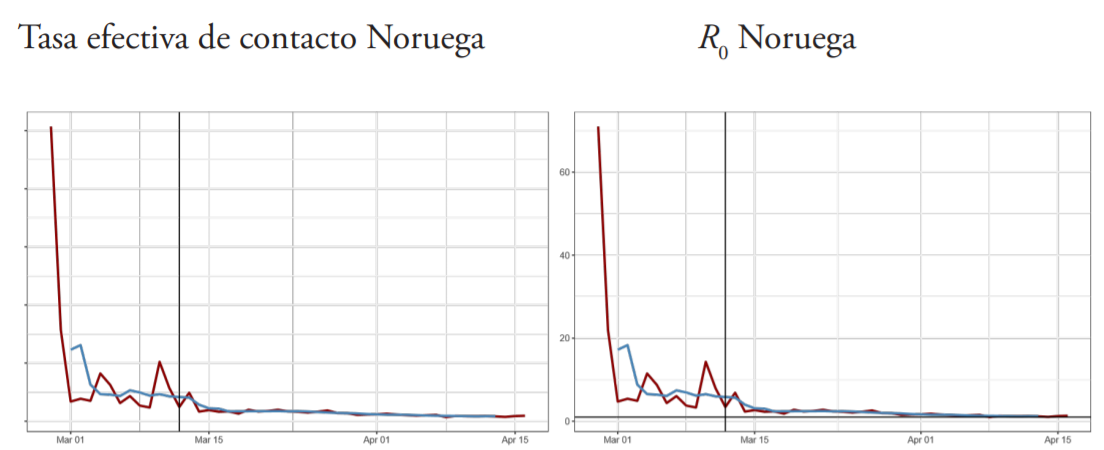
Del resto de los países evaluados, Italia, Corea del Sur y Noruega lograron la mayor disminución en sus tasas de contacto, con caídas de al menos un 90 % desde sus niveles picos hasta la fecha, lo que contribuyó a que el número de contagios secundarios de la última semana se ubique por debajo del 1.4, inferior al rango mínimo estimado por la OMS para el COVID-19¹². A este logro se suman Australia, Austria, China y Hong Kong.

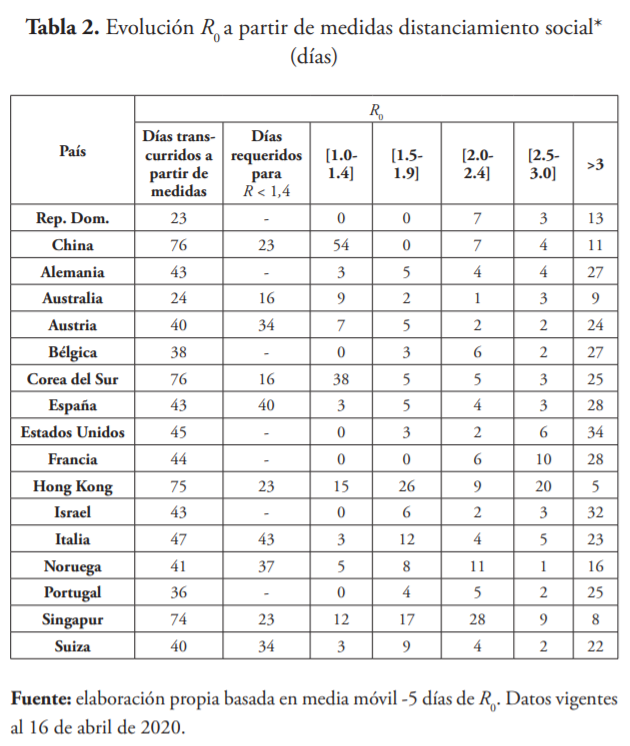
Una forma alternativa de evaluar el impacto de las medidas de las autoridades es analizar el tiempo que requirió cada país en reducir R₀ a los niveles actuales (véase tabla 2). En la tabla se aprecia que a partir de la adopción de las medidas de distanciamiento, la República Dominicana requirió 13 días para reducir los contagios secundarios a menos de tres, lo que se compara favorablemente con el resto de los países evaluados y dista de los 34 días requeridos por Estados Unidos, el mayor tiempo entre los países evaluados. 

De los países que redujeron sus contagios secundarios a menos de 1.4, Italia y España (epicentro europeo de la pandemia) fueron los que requirieron más tiempo para hacerlo (43 y 40 días, respectivamente); en tanto Australia y Corea del Sur solo necesitaron 16 días, los más rápidos en hacerlo.

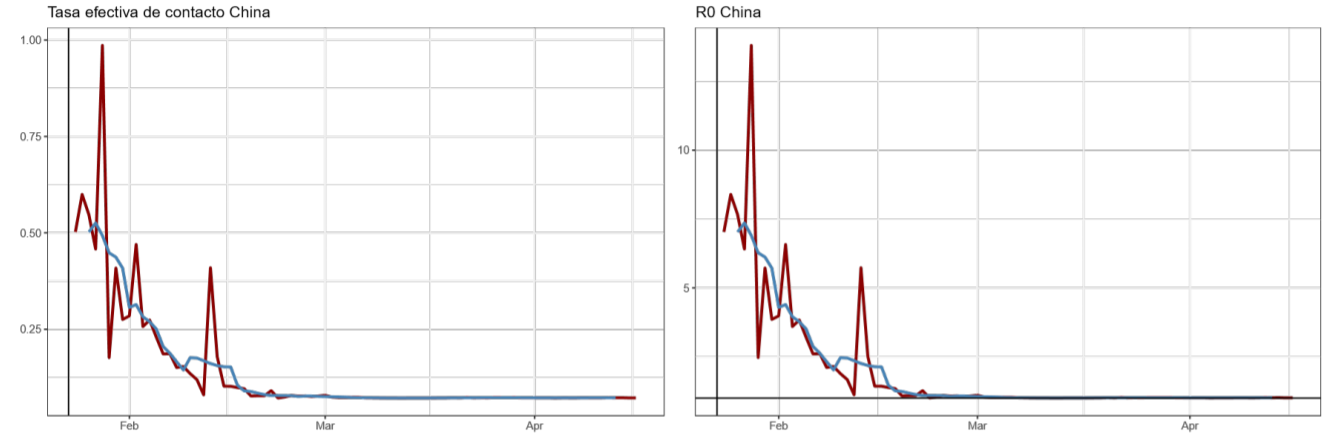
La tabla también revela la clave de países que han sido exitosos en contener el virus; tal es el caso de China, que no solo logró disminuir sus contagios secundarios a niveles menores de 1.4 en un tiempo reducido¹³, sino que ha sido el país que más tiempo se ha mantenido en estos niveles, en concreto, 54 días consecutivos¹⁴. 

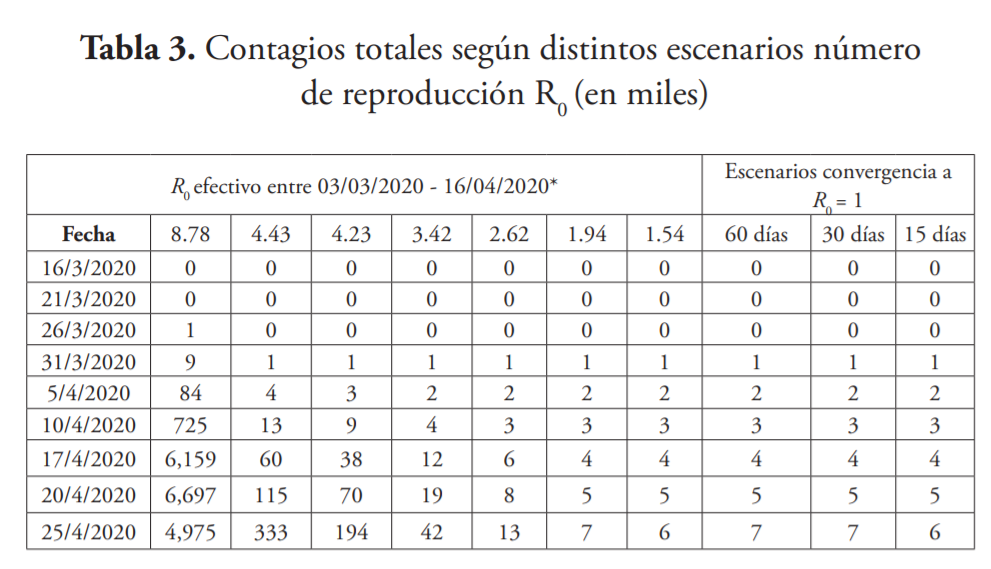
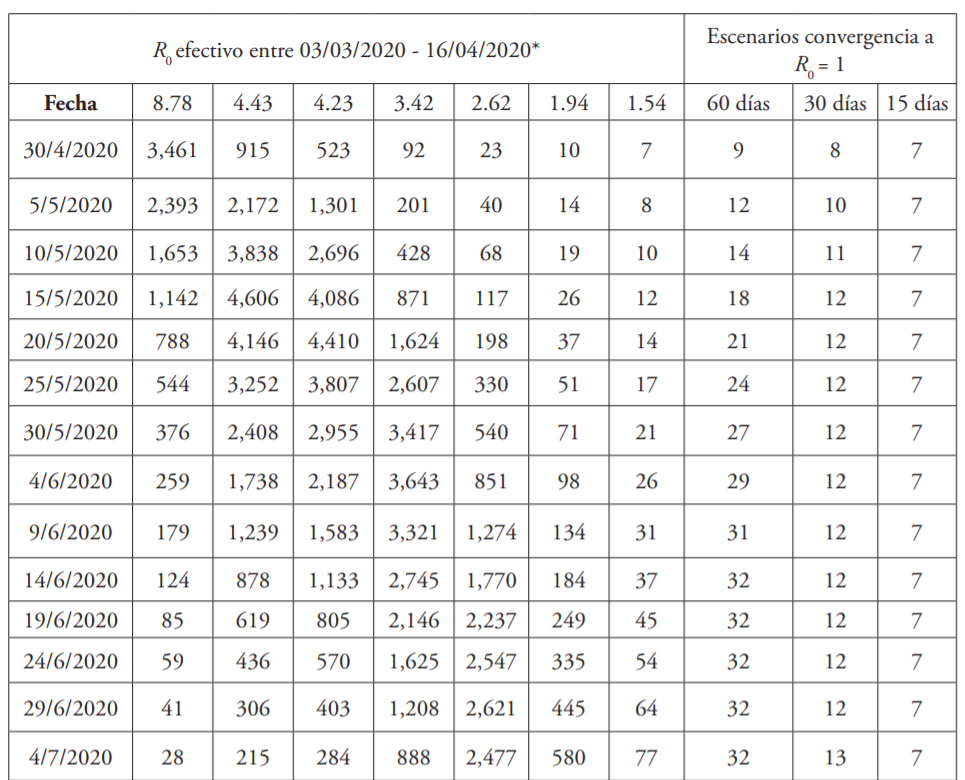
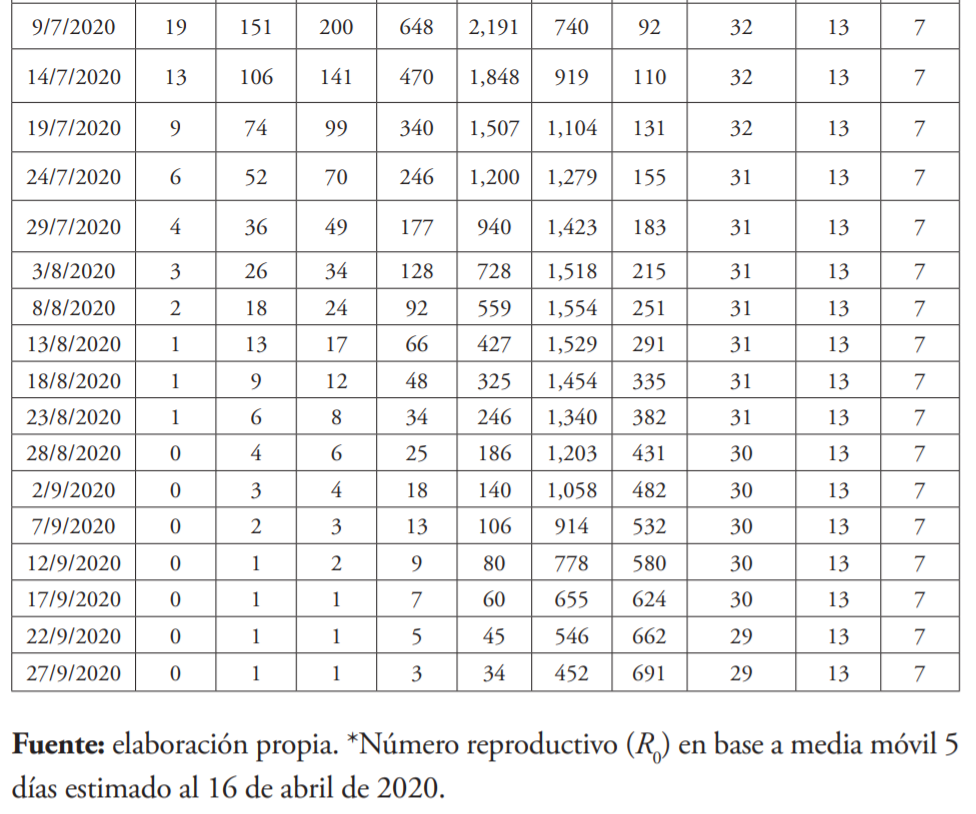
Para evaluar estos resultados en términos del número de infectados en la República Dominicana, en la tabla 3 se presenta la cantidad de contagiados diarios asociados a distintos números reproductivos, al cierre de cada semana laboral durante los últimos 21 días. Se puede apreciar que las políticas de distanciamiento han desacelerado el ritmo de crecimiento de los infectados. De hecho, si las autoridades no hubiesen adoptado las medidas hoy vigentes, cada nuevo infectado hubiese contagiado a alrededor de nueve, llevando la cifra de contagios a poco más de 6.7 millones de personas¹⁵. 

Las cifras anteriores no deben ser subestimadas. A modo de ejemplo, si se considera una tasa de mortalidad de un 2 %, equivalente a la inicialmente comunicada por la OMS para COVID-19¹⁶, esos resultados suponen haber impedido el fallecimiento de, al menos, 130,000 seres humanos.

Las estimaciones al 16 de abril de 2020 indican que el R₀ alcanzó 1.54, el mínimo nivel desde que iniciaron las medidas de distanciamiento, aunque todavía superior al umbral de 1, lo que garantiza la expansión del virus. De mantenerse estas condiciones, el virus se propagaría infectando a un máximo de un 7 % de la población, en tanto su máximo nivel de nuevos contagios semanales¹⁷ alcanzaría cerca de 51,000 personas hacia septiembre de 2020, lo que evidencia la necesidad de extender y fortalecer las políticas de distanciamiento social. 

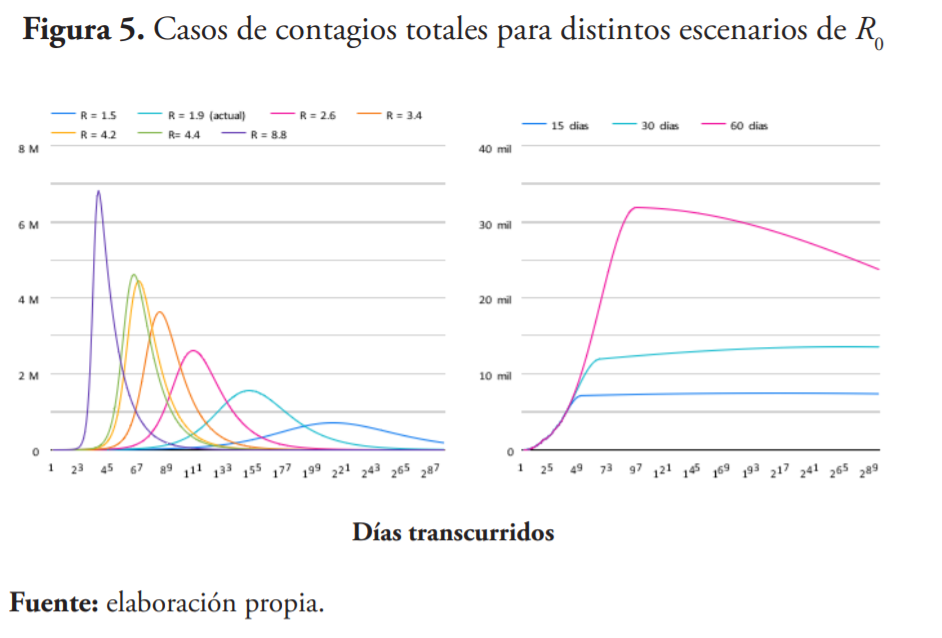
Si tomamos como referencia las efectivas estrategias de contención adoptadas por China y Corea del Sur y lográsemos reducir los contagios secundarios desde los niveles vigentes a valores inferiores a 1.1 en los próximos 60 días, el mayor nivel de infectados rondaría los 32,000, con un nivel máximo de nuevos contagios semanales cercanos a los 3,200 hacia mediados de mayo. De hacerlo en los próximos 30 días, el máximo nivel de contagios no superaría los 13,500, en tanto el mayor nivel de nuevos infectados semanales ocurriría hacia finales de abril, con un tope rondando los 1,700 casos.

Los resultados para República Dominicana, bajo el contexto de la experiencia internacional evaluada, destacan la importancia del uso del número de contagios secundarios R_t , como métrica relevante para diagnosticar la evolución de la epidemia.

5. Conclusiones

La mitigación del COVID-19 lidera la lista de prioridades de las principales autoridades públicas y privadas a nivel global, debido al impacto humanitario, social y económico que genera una propagación no gestionada adecuadamente.

En ese contexto, este documento cumple un doble propósito. Primero, contribuye al estudio de la evolución de epidemias, adaptando el enfoque de estado-espacio, usado regularmente en el ámbito de pronósticos econométricos, al modelo epidemiológico canónico (SIR). Dicha adecuación permite capturar la dinámica de los principales parámetros del modelo, tradicionalmente asumidos como constantes, lo que resulta en pronósticos de contagios más realistas. 

En segundo lugar, este trabajo se constituye como un marco metodológico útil para los hacedores de política, en tanto permite diagnosticar la evolución de la pandemia en términos de su tamaño final, el momento en que alcanza su pico y bajo cuáles condiciones se disipa, a partir de las políticas de distanciamiento adoptadas.

En ese sentido, aplicando dicho marco al análisis de la evolución del COVID-19 en la República Dominicana y un grupo de países seleccionados, se observa que las políticas de distanciamiento han contribuido a reducir la propagación del virus, lo que se refleja en una tendencia decreciente del número básico de reproducción R₀ , esto es, la cantidad de contagios adicionales que provoca un infectado nuevo¹⁸.

A nivel global, China y Corea del Sur han sido los países más efectivos conteniendo la propagación, no solo por la rapidez en que redujeron R₀ , sino porque han logrado situarlo alrededor del umbral de 1, de forma sostenida; en el caso particular de China, durante más de 50 días.

En cuanto a República Dominicana, la caída observada de R₀ , desde nueve contagios secundarios promedio, previo a la adopción de políticas de distanciamiento, a dos contagios, posterior a estas, en tan solo 20 días, supera los declives observados en Francia y Estados Unidos durante el mismo período.

En las próximas semanas, las decisiones que adopten las autoridades, en adición a las conductas que asuma la población, determinarán si la tendencia decreciente observada en el número de contagios secundarios retrocede, aumentando la propagación del virus, o continua su descenso tanto como para aplanar la curva y salvar vidas.

De retroceder, las estimaciones hechas al 16 de abril de 2020 señalan que, bajo el escenario en que R₀ se estabiliza en los niveles actuales, la pandemia se propagaría lo suficiente para contagiar a alrededor del 7 % de la población, con una cifra máxima de nuevos contagios cercana a los 51,000 casos semanales; esto ocurriendo hacia septiembre de 2020.

De continuar su tendencia decreciente y estabilizarse en los próximos 30 días en valores cercanos a 1, tal como ocurre en China y Corea del Sur, el máximo nivel de nuevos contagios rondaría los 13,500; en tanto el mayor nivel de nuevos infectados semanales alcanzaría los 1,700 casos hacia finales de abril de 2020. Estas cifras evidencian la necesidad de extender y fortalecer las medidas vigentes, al igual que destacan la importancia de monitorear el número de contagios secundarios, R_t , como métrica relevante para diagnosticar la evolución de la epidemia.

Anexos

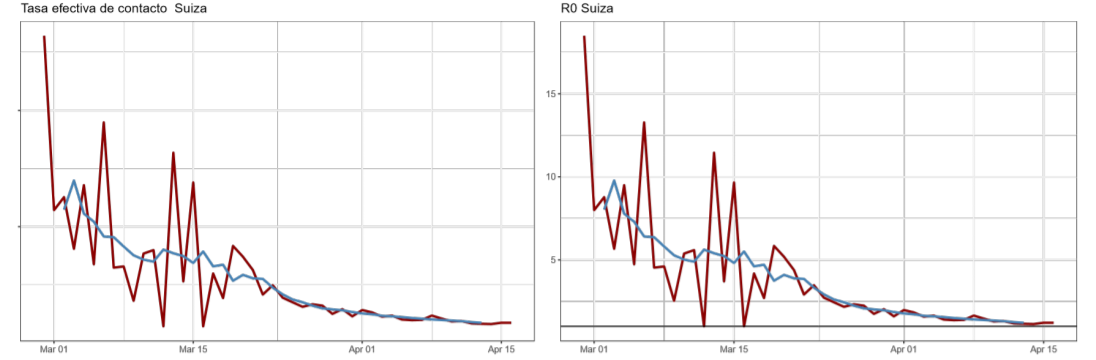
A. Trayectoria de la tasa efectiva de contacto (β_t ) y número básico de reproducción R₀ estimados con el modelo estado-espacio (enero abril de 2020)

Fuente: elaboración propia.

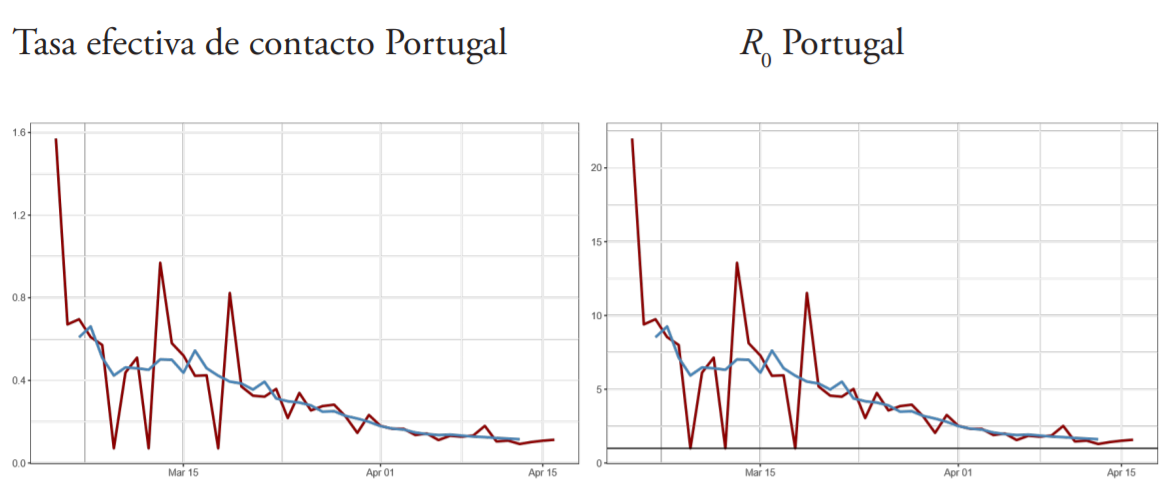
Fuente: elaboración propia.

Fuente: elaboración propia.

Fuente: elaboración propia.

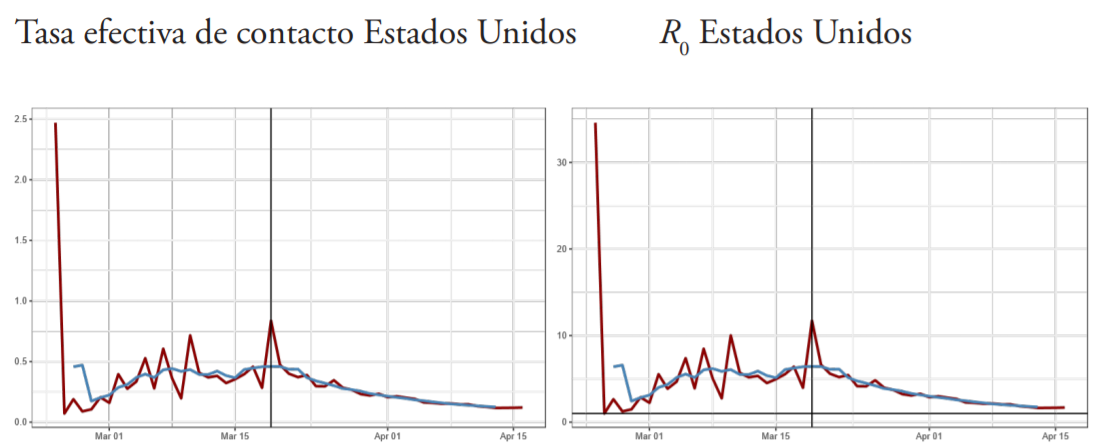
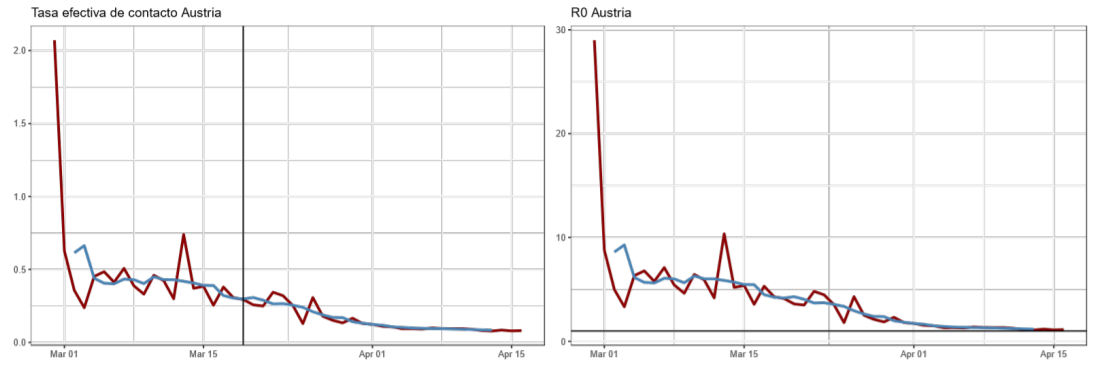
Fuente: elaboración propia.