Modelo de minimización de los costos totales de la cuarentena y la pandemia: aplicaciones y estimaciones para el caso de República Dominicana

Introducción

Las medidas de aislamiento social (cuarentena) se imponen para reducir la velocidad de propagación de una pandemia. Esa reducción disminuye la cantidad de individuos infectados y, dada la tasa de mortalidad de esta población, se reduce la cantidad de muertes, lo que representa una reducción del costo de la pandemia o un beneficio, el cual puede ser medido a través de la aplicación de los criterios de la teoría del valor estadístico de una vida humana (Kniesner & Viscusi, 2019).

En el marco de esta teoría, el valor estadístico de un año de vida es aquel que la sociedad está dispuesta a pagar para evitar que se pierda ese año de vida. En el enfoque estándar aplicado, el valor esperado de la reducción del riesgo de mortalidad se igualaría al valor presente esperado de los ingresos perdidos y los costos de la atención médica. El valor de los años estadísticos de vida, cuya pérdida se evita con la cuarentena, es el principal beneficio que esta produce.

A pesar del beneficio medido en términos de años estadísticos de vida salvados, el distanciamiento social también tiene costos significativos, representados por el valor agregado dejado de producir por la población laboral en cuarentena o por las pérdidas que produce la paralización económica. En este enfoque teórico del análisis de los beneficios y los costos del aislamiento social y de la pandemia se parte del supuesto de que ambas variables se pueden identificar y medir con precisión, lo cual podría ser cuestionable cuando la medición del costo de la cuarentena se mide a través de las pérdidas en términos de PIB, tal y como lo hace Thunstrom, Newbold, Finnoff, Ashworth & Shogren (2020).

Mientras mayor sea la cantidad de años estadísticos de vida que la cuarentena evita perder; mientras mayor sea el ingreso o el valor agregado futuro dejado de producir; y mientras menor sea la tasa con que se descuenta dicho ingreso o valor agregado futuro, mayor será el beneficio de colocar la cuarentena. Si todas las otras variables se mantienen constante, a mayor ingreso per cápita, o a mayor salario, mayor será el beneficio de la cuarentena, pues mayores serán los ingresos asegurados por el valor estadístico de los años de vida salvados y, si se asume que esta cuarentena no tiene costos, el beneficio se obtiene al aplicar la ecuación de años estadísticos de vida salvados a los datos de la población existente.

El supuesto de la no existencia de costo de la cuarentena es el enfoque y el procedimiento utilizado por Greenstone & Nigam (2020), quienes calculan los beneficios de la cuarentena o el distanciamiento social en Estados Unidos, aplicando directamente el valor estadístico de los años de vida salvados al producto de la diferencia entre la cantidad de fallecidos, con y sin distanciamiento social. Estos autores utilizan una proyección de la reducción de la mortalidad por grupos de edad para calcular un promedio del valor estadístico de un año de vida salvado por el distanciamiento social, lo que los conduce a la conclusión de que, bajo los supuestos utilizados, un distanciamiento social de tres a cuatro meses produce un beneficio de 8 trillones de dólares, resultado que debe ser evaluado tomando en cuenta que este depende fundamentalmente del ingreso per cápita perdido durante los años estadísticos de vida calculados.

Descripción del modelo

Para estimar el costo de la pandemia es necesario partir de un modelo matemático tipo SIR (Susceptibles, Infectados, Recuperados). En este tipo de modelo (Fresnadillo-Martínez, García-Sánchez, García-Merino, Martín del Rey, & García-Sánchez, 2013) se parte de una población de N individuos compuestos por los Susceptibles (S), los Infectados (I) y los Recuperados (R).

El brote aparece y se inicia el conteo de casos positivos en el período t, resultando una cantidad acumulada de individuos de I₀ . Cada individuo infectado contagia a una cantidad j de nuevos individuos por período de tiempo. Del total de infectados se recupera una cantidad R. El grupo mayoritario de individuos, S_e , está expuesto al contagio. Según el modelo SIR estándar de Kermack & McKendrick, ampliado por el de Hethcote para incluir la tasa de mortalidad (ambos citados por Fresnadillo-Martínez et al., 2013), en el siguiente período la cantidad de individuos susceptibles, infectados y recuperados vendría dado por cada una de las siguientes ecuaciones:

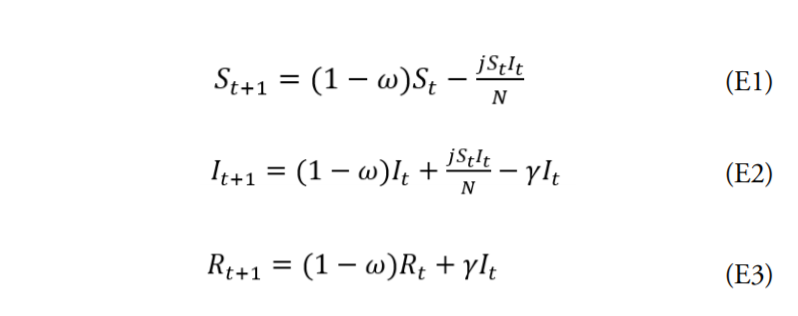
En donde γ es la tasa de recuperación de los infectados y la tasa de mortalidad. En una situación sin cuarentena la cantidad de fallecimientos esperados en el período t+1 sería igual a ωI_sct+1. Si la cantidad de vida promedio esperada perdida por cada individuo es T años (igual a la esperanza de vida menos la edad promedio de los fallecidos por la pandemia) y el ingreso promedio anual de cada individuo es Q₁ , entonces el Costo Esperado de la Pandemia Sin Cuarentena (CEPSC) vendría dado por la siguiente ecuación:

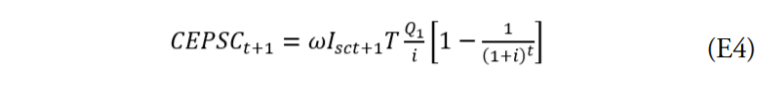
En la que i es la tasa de descuento a la que sociedad valora los años de vida perdidos. Obsérvese que en esta ecuación el costo de la pandemia es el producto de la cantidad de años de vida perdidos (ωI_t+1T) por el valor estadístico de un año de vida humana ($\frac{Q1}{i}=\left[1-\frac{1}{{(1+i)}^t}\right]$ ). En la ecuación anterior, todas las derivadas parciales de la variable dependiente con respecto a cada una de las variables independientes son positivas y mayor que cero. Con todas las demás variables independientes fijas el costo de la pandemia es una función creciente con respecto a la cantidad de infectados esperados.

En una situación con cuarentena el número de casos de individuos infectados sigue aumentando, aunque el efecto esperado de la cuarentena es que el crecimiento sea menor que sin ella, debido a la reducción de la variable j de la ecuación 2. Por tanto, lo único que cambia en la ecuación anterior es la cantidad de infectados, la cual se sustituye por la cifra esperada en la situación con cuarentena:

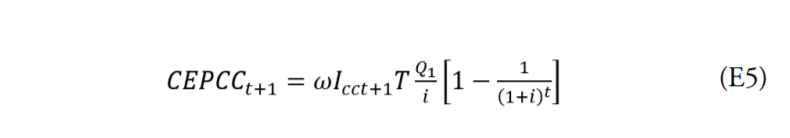
Por tanto, el Beneficio de la Cuarentena, o Costo de la Pandemia con Cuarentena, viene determinado por la diferencia entre la cantidad de infectados con y sin esta:

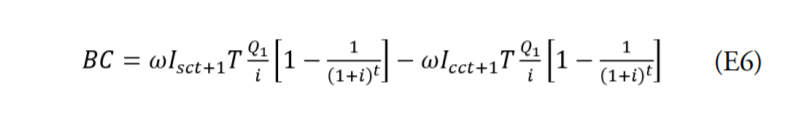
Si se toma en cuenta la diferencia en el número de infectados con y sin cuarentena, entonces la ecuación anterior equivale a sustituir dicha diferencia por la reducción que la cuarentena produce la variable j de la ecuación 2:

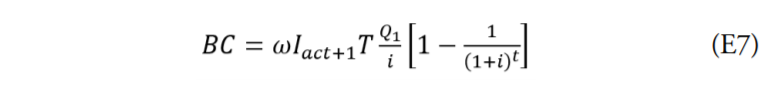
En la que I_act+1 representa la cantidad de infectados ajustada por los efectos de la cuarentena mediante la reducción de la variable j, la cual representa el factor de propagación, el cual cae como resultado de la cuarentena.

Para formular una ecuación que refleje correctamente el costo de la cuarentena, es necesario tomar en cuenta que el modelo aquí empleado se fundamenta en la cantidad de individuos, y si el costo de esa cuarentena depende del ingreso que generan los individuos puestos bajo esta, entonces ese costo depende exclusivamente de aquel ingreso y de la cantidad de individuos infectados. Lo anterior significa que, en términos de la cantidad de individuos, el costo de la cuarentena es el valor agregado que generaba toda la fuerza laboral antes de la cuarentena, la cual siempre sería mucho menor que toda la población susceptible de la ecuación 1.

Con una población laboral ocupada igual a S_pltplt+1-αI_t+1, en donde $a=\frac{S_{plt}}{N}$. Si Q2 es el valor agregado por trabajador ocupado, entonces el costo esperado de la cuarentena vendría dado por la siguiente ecuación:

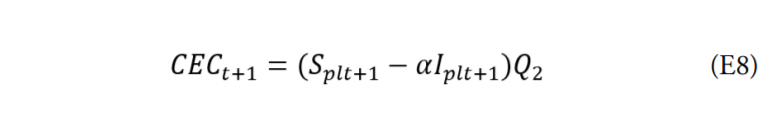
La ecuación 7 es la diferencia del costo de la pandemia con y sin cuarentena, es decir, el beneficio de esta, y la 8 representa su costo. La situación óptima es aquella en la que el beneficio se iguala a sus costos, o lo que es lo mismo, la minimización de la suma del costo de la pandemia con cuarentena y el costo de ella, lo que significa la igualación de ambas ecuaciones:

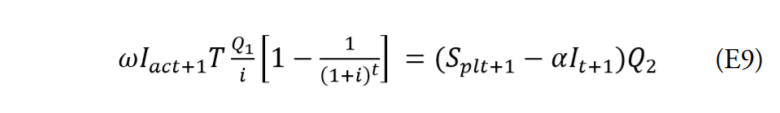
La ecuación 9 representa la relación fundamental del intercambio entre el costo de la pandemia con y sin cuarentena (beneficios de la cuarentena); el lado derecho representa el beneficio, es decir, el costo de la pandemia con cuarentena, y el lado derecho el costo de esta. La ecuación podría tener profundas implicaciones para la toma de decisiones, tales como el momento de imponer o levantar la cuarentena, el riesgo de resurgimiento de la pandemia aceptable, y para los criterios de priorización de las inversiones a realizar para reducir esos riesgos.

Uno de los primeros elementos a tomar en consideración, que surge del análisis de la ecuación 9, es que mientras el costo (beneficio de la cuarentena) de la pandemia es una función creciente de la diferencia entre el número esperado de contagios con y sin cuarentena (a mayor número de contagios evitados, mayor beneficio), el costo de esa cuarentena es una función decreciente del número esperado de infectados sin cuarentena, pues mientras mayor es la cantidad de infectados (los cuales entran a la población de contagiados), menor es la población productiva o laboral en cuarentena.

La interpretación de la ecuación 9 significa que el beneficio de la cuarentena aumenta con el número de contagios evitados por esa cuarentena, mientras que el costo de ella disminuye con el número de contagios observados; tal y como se desprende del análisis e interpretación matemática de la citada ecuación, la velocidad a la que aumenta el beneficio (pendiente positiva) es mucho mayor de la que disminuye el costo (pendiente negativa).

Lo anterior se puede ilustrar en el siguiente gráfico, en el que la curva de los beneficios de la cuarentena, BC, se ha trazado en base al número de contagios o Infectados con cuarentena, Icc; mientras que el costo de la cuarentena, CC, ha sido trazado en base al número de Infectados sin cuarentena, Isc, y en el que el punto de intersección de ambas curvas representa una situación de minimización de la suma de los costos de la pandemia con cuarentena y el costo de esta:

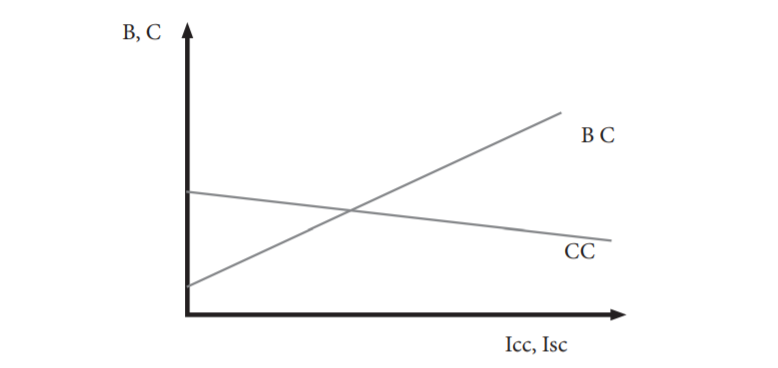
La primera conclusión que se desprende del gráfico anterior y de las ecuaciones que lo originan es que la cuarentena no debe imponerse desde el mismo instante en que aparece la pandemia, pues a la izquierda del punto de intersección de ambas curvas el número de infectados en la situación con cuarentena es mayor que en la situación sin cuarentena y, por consiguiente, el costo de la cuarentena siempre será mayor que el beneficio de esta.

La segunda conclusión fundamental es que cuando el número de infectados se coloca por encima del punto de intersección es conveniente imponer el confinamiento o cuarentena, pero teniendo en cuenta que esta reduciría el factor de propagación, lo que empujaría la curva de beneficio hacia abajo y la curva de costo hacia arriba. La cantidad de infectados con cuarentena siempre será posible de calcular y comparar con la cantidad que existiría en la situación sin cuarentena, pero en este caso no existe un mecanismo de mercado que asegure un proceso de ajuste que conduzca al punto de equilibrio.

Es necesario alertar y señalar que el cálculo de las ecuaciones de las curvas del gráfico anterior estaría sujeto a grandes riesgos e incertidumbres, pues este depende de la validez de la fijación o elección de los parámetros básicos y, lo que es igualmente importante, los resultados finales son altamente sensibles a cualquier cambio en dichos parámetros, todo lo cual conduce a la conclusión general de que las decisiones de imponer o retirar la cuarentena siempre estarán sujetas a un gran margen de error.

A diferencia del modelo utilizado por Thunstrom, Newbold, Ashworth & Shogren (2020), el cual utiliza como costo de la cuarentena la diferencia del PIB entre una situación con y sin cuarentena (lo cual no es observable), el representado por la ecuación 9 utiliza el ingreso total o valor agregado de la cantidad de la fuerza laboral como base para el costo de esta. Este fundamento microeconómico, centrado en el costo directo, fundamentado en variables observables o estimables, permite evaluar decisiones relacionadas con el momento adecuado de levantar la cuarentena, la evaluación del riesgo de resurgimiento, y de las inversiones orientadas a reducir el riesgo e incidencia de la pandemia. 

Estimaciones de costos y beneficios para el caso dominicano

La aplicación del modelo aquí expuesto, representado por la ecuación 9, requiere de la fijación de las variables independientes y parámetros de este, y por supuesto, los resultados dependen de los valores que se utilicen. Suponiendo que el plazo mínimo de las cuarentenas es de 10 días, en el cuadro que sigue se presentan las estimaciones de los costos y los beneficios de la cuarentena anticovid del caso dominicano, especificando en el encabezado los valores de los parámetros y las variables utilizados en esas estimaciones.

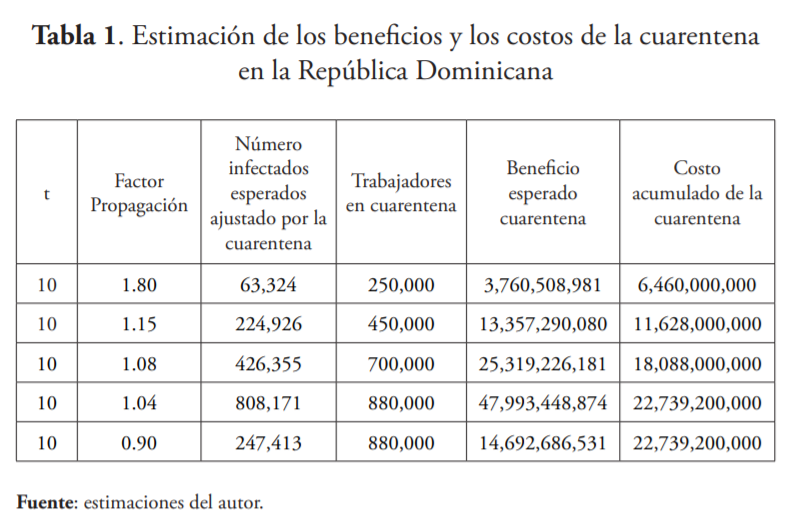
Q1 es el valor agregado promedio por trabajador ocupado, descontado en un 30 % para tomar en cuenta el efecto de una posible actividad productiva de los sectores o las ramas de las empresas formales que suspendieron sus trabajadores. Q2 es el ingreso laboral promedio diario; w es la tasa de mortalidad aceptada por organismos internacionales; T es el número de días perdidos con cada fallecimiento a causa de la pandemia; e i es la tasa de descuento del 10 % utilizada en el ejercicio.

La primera columna representa bloques o quántum de tiempo de diez días, período en que varía el promedio del factor de propagación presentado en la segunda columna. El primer quántum de diez días se inició con un factor de propagación de 1.8, variable que, una vez introducida junto a las anteriores, producen como resultado la cantidad de infectados esperados ajustados, los beneficios en términos del valor de los años de vida estadísticos, cuya pérdida evita la cuarentena, y el costo de esta, medidas esta última para el período total de los diez días de cada quántum.

En los siguientes tres períodos los beneficios son mayores que los costos, ampliándose la diferencia hasta llegar a más que duplicarlo en el tercer período. A diferencia de los primeros cuatro períodos, cuyas estimaciones se realizaron con datos reales observados, en el quinto y último quántum se supone que la tasa de propagación baja hasta 0.9 y, como era de esperarse, según lo que predice el modelo, el costo de la cuarentena se hace significativamente mayor que su beneficio, indicando o sugiriendo que desde que este sea menor que la unidad, es el momento de levantar la cuarentena.