Participación en cadenas globales de valor e industrias claves: evidencia de Puerto Rico

1. Introducción

El esquema operativo de las cadenas globales de valor (CGV), visto desde la perspectiva de país, provoca que numerosos bienes y servicios crucen distintas fronteras nacionales con el calificativo de productos intermedios, con la intención de ser sometidos a la lógica productiva en la que cada país — encadenado comercialmente de manera vertical— le añade cuotas de valor, hasta que estén listos para ser entregados a su último destino como productos finales para consumo o capital (Sturgeon, 2001; Sturgeon y Gereffi, 2009; Gereffi, Humphrey y Sturgeon, 2005).

A pesar de no ser un fenómeno nuevo, la habilidad de los productores —sobre todo empresas multinacionales (EMN)— de “cortar hacia arriba” la cadena de valor (Krugman, 1995, p. 15) en busca de ventajas de costos para ser más competitivos a nivel global aprovechando las asimetrías tecnológicas (Banga, 2013; Durán y Zaclicever, 2013), agudiza la fragmentación geográfica del “modo de producción verticalmente integrado denominado fordista” (Feenstra, 1998, p. 31).

Esta realidad ha provocado un “cambio fundamental” en la estructura del comercio y los negocios internacionales hasta el punto de haber creado una “nueva realidad comercial” (Instituto de Economías en Desarrollo/ Organización Japonesa de Comercio Exterior/Organización Mundial del Comercio, 2011, pp. 3-4; Foro Económico Mundial, 2012; Comisión Económica para América Latina, 2014; Kowalski, Lopez, Ragoussis, Ugarte, 2015).

Más aún, desafía a los académicos y hacedores de políticas a repensar no solo las teorías fundamentales del comercio exterior, sino también los instrumentos metodológicos con los que se elaboran sus indicadores para la toma de decisiones, en temas que van desde el problema de la “múltiple contabilización bruta” en el valor de las exportaciones mundiales, agudizado por el creciente comercio de intermedios, la denominación del “país de origen”, hasta el “comercio de valor añadido” (United Nations Conference On Trade and Development, 2013, p.123; Maurer y Degain, 2012, p. 2; IED/JETRO/OMC, 2011).

Empujar las fronteras de investigación en este contexto globalizado, requiere “interdisciplinariedad” y cierta “conectividad creativa” en tiempos donde la pregunta de a quién beneficia deviene más apremiante y la respuesta más sofisticada (Buckley y Ghauri, 2004, pp. 91-92). Más aún, explorar trayectorias y escenarios alternativos que ayuden a que el progreso económico de las empresas envueltas en su esquema, se traduzca también en escalamiento social de los trabajadores (Barrientos, Gereffi, y Rossi, 2011; Rossi, 2013; Kaplinsky, 2010).

En esta encrucijada, uno de los indicadores de reciente invención y aplicación es el que intenta medir el grado aproximado de participación de un país en las CGV utilizando las matrices insumo producto (MIP) de la contabilidad nacional (Zaclicever 2018, 2017; Ahmad, Bohn, Mulder, Vaillant, y Zaclicever, 2017; De Backer y Miroudot, 2013; Koopman, Power, Wang, y Wei, 2011, 2012; CEPAL, 2018).

El presente ensayo utiliza las MIP de Puerto Rico disponibles para realizar esta primera aproximación descriptiva y medir específicamente el grado agregado de participación hacia atrás y compararlo a nivel internacional. Luego, identifica las principales industrias de manufactura que participan en este esquema y las clasifica según la tecnología de sus exportaciones de acuerdo a la lógica propuesta por Lall (2000). Finalmente, analiza hasta qué punto estas industrias son claves para la economía nacional en términos de creación de eslabonamientos hacia atrás y hacia adelante, aplicando las métricas más utilizadas en el modelo insumo-producto (Temurshoev y Oosterhaven, 2013).

Además de coadyuvar a cerrar la brecha de las contribuciones empíricas de los países latinoamericanos y del Caribe sobre el tema, aporta un modo comprehensivo al modelo insumo-producto desde el trasfondo teórico sobre el que descansa, con el objetivo de facilitar futuras replicaciones en otros países.

En la segunda sección se presenta la revisión de literatura. En la tercera, la metodología, que incluye la descripción, supuestos, desarrollo del modelo y los datos. En la cuarta, la discusión de los resultados. En la quinta, las limitaciones y futuras investigaciones. La sexta, las conclusiones.

2. Revisión de literatura

2.1 Índice de participación en cadenas globales de valor

Un grupo de economistas de la División de Investigación de la Oficina de Economía de la Comisión de Comercio Internacional de Estados Unidos, fue el primero en proponer explícitamente un índice de participación en CGV de un país, mediante la descomposición detallada del valor añadido de sus exportaciones brutas utilizando matrices de insumo producto internacionales (Koopman et al., 2011).

Koopman et al. (2011) conciben este índice, como el resultado de la suma del valor añadido doméstico que de modo indirecto exporta a terceros países y el valor añadido extranjero de sus exportaciones, expresados en proporción de sus exportaciones totales. De Backer y Miroudot (2013) bautizaron estos sumandos con el nombre de índice de participación hacia adelante y hacia atrás, respectivamente.

A partir de estos trabajos, el índice de participación hacia adelante de un país se concibe como un indicador relativo al vínculo “aguas abajo” en la cadena de valor de sus exportaciones, en tanto que son utilizadas como insumos intermedios para la producción de otras exportaciones a terceros, captando el lado de la oferta. Mientras que el índice de participación hacia atrás, hace referencia al vínculo “aguas arribas”, en tanto que sus exportaciones necesitan importar insumos para ser producidas, captando el lado de la demanda (Zaclicever, 2018, 2017; Ahmad et al., 2017; De Backer y Miroudot, 2013).

2.2 Antecedentes

Koopman et al. (2011) crean el índice con base en la extensión y ajuste de las fórmulas que Hummels, Rapoport, y Yi (1998) y Hummels, Ishii, y Yi (1999, 2001) llaman índice de especialización vertical (VS y VS1). Sin embargo, Hummels et al. (2001) calculan y definen matemáticamente el VS (participación hacia atrás) dado que solo disponían de MIP nacionales y no internacionales, indispensables para el cálculo del VS1 (participación hacia adelante).

Asimismo, reconocen que el VS es la ecuación matemática que han utilizado “los economistas del desarrollo” desde Chenery y Watanabe (1958) para capturar el contenido importado de las exportaciones y que toma de esta corriente de pensamiento para insertarlo conceptualmente al fenómeno de la especialización vertical en la tradición de los economistas del comercio desde Balassa (1967), Findlay (1978) y Sanyal (1983) (Hummels et al., 2001, p. 81). 

Además, son conscientes de que el valor del VS es equivalente al valor añadido foráneo incorporado en las exportaciones, siempre y cuando solo existan dos etapas de producción. Si ocurren más de dos etapas en el proceso productivo, y/o un país reimporta algo de su propio valor añadido para ser usado como insumo en otros bienes que luego son exportados, entonces el valor añadido foráneo es menor que el valor del VS (Hummels et al., 2001, p. 88).

En definitiva, Hummels et al. (2001) calculan el índice de participación hacia atrás en CGV bajo los supuestos señalados y con el nombre de especialización vertical (VS), de 14 países (11 de la Organización para la Cooperación y el Desarrollo Económicos (OCDE), más Irlanda, Corea y Taiwán). Entre los hallazgos se encuentra que el VS experimenta un crecimiento combinado en el período comprendido entre 1970 y 1990 de 16.5 % a 21 % aproximadamente, excepto Japón, en el que decrece. 

2.3 Aplicaciones

La tabla 1 presenta una relación de ensayos seleccionados que calculan el índice de participación hacia atrás en cadenas globales de valor como VS.

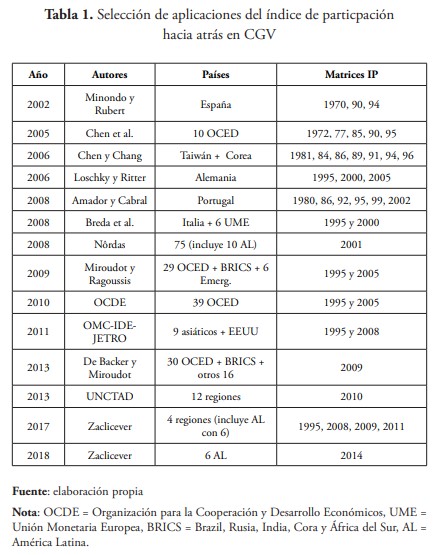
Destacamos la extensión que realizan Chen, Kondratowicz, y Yi (2005) que confirma la ligera tendencia al alza del índice a partir de los años 90, excepto en Japón y Dinamarca. Otro aporte, es el haber realizado el ejercicio con deflactores industriales para la producción bruta y para el total de importaciones, confirmando que usar razones nominales o reales no hace diferencia significativa a la hora de estimar el índice (Chen et al., 2005).

Nôrdas (2008) fue el primer estudio de esta índole que incluye países latinoamericanos (Argentina, Bolivia, Brasil, Chile, Colombia, Ecuador, México, Perú, Uruguay y Venezuela). Con ellos suma un total de 75 a los países que calcula el índice para 2001 arrojando un promedio de 26 %. Encontró, además, que los países en desarrollo de Asia tienen mayores índices de participación hacia atrás en CGV que los países en desarrollo de Latinoamérica.

Asimismo, De Backer (2010) actualizó el índice para 39 países miembros de la OCDE para 1995 y 2005. Solo en tres naciones decreció el índice, el resto experimentó crecimiento.

Del mismo modo, UNCTAD (2013) calcula el VS para 2010 en 12 regiones mundiales; a saber: la Unión Europea, Estados Unidos y Japón (que las llama economías desarrolladas); África, Asia (este y sudeste, sur y oeste) y América Latina (centro y sur) y el Caribe (que las agrupa en economías en desarrollo); y, por último, una región que llama economías en transición. Los resultados arrojan un índice de 31 % para Centroamérica, 21 % para el Caribe, y 14 % para Suramérica. El este y sudeste asiático ostentan un 30 % y Japón y los Estados Unidos un 18 % y un 11 %, respectivamente.

Zaclicever (2017) por su parte, calcula el índice de modo regional para cuatro años distintos (1995, 2008, 2009, 2011) en las denominadas tres “fábricas” o “factorías” de América del Norte, Europa y Asia (CEPAL, 2013) para compararlas con la región que llama “Latinoamérica” en la que incluye seis países (Argentina, Brasil, Chile, Colombia, Costa Rica, Perú). Entre sus hallazgos está que Costa Rica ostenta el mayor nivel de participación entre los países latinoamericanos estudiados con un 29 % (1995), 40 % (2008), 37 % (2009) y 39 % (2011). En este último año, este país ronda el promedio de la factoría Asia de 40 %, que comprende entre un 18 % (Japón) y un 57 % (Cambodia). México, por su parte, exhibe un índice de 44 % en 2011.

Finalmente, Zaclicever (2018) actualiza el VS de los 6 países latinoamericanos del estudio anterior con México, para el año 2014. Sus resultados colocan a Argentina y Brasil con un 15 %, Chile (20 %), Colombia (9 %), Costa Rica (34 %), Perú (13 %) y México (38 %).

2.4 Eslabonamientos e industrias claves

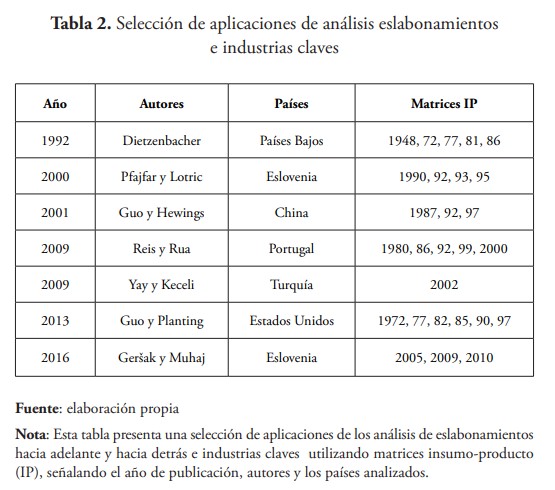
Temurshoev y Oosterhaven (2013) distinguen al menos diez indicadores que intentan medir los eslabonamientos e identificar las industrias claves basados en las ideas de desarrollo endógeno de Hirschman (1958). 

Los más utilizados para los eslabonamientos hacia atrás son los enlaces directos de Chenery y Watanabe (1958) y los totales de Rasmussen (1956) con la matriz inversa de Leontief. Para los vínculos hacia adelante, los totales de Jones (1976) utilizando la matriz inversa de Ghosh (1958).

La tabla 2 presenta ensayos seleccionados que utilizan las MIP nacionales para identificar eslabonamientos e industrias claves.

3. Metodología

3.1 Modelo: descripción y supuestos

Para derivar el índice de participación hacia atrás de un país en CGV, pese a que ni Hummels et al. (2001) ni Koopman et al. (2011) lo explicitan, se desarrolla el modelo cuantitativo abierto de Leontief (1936, 1937) quien realiza un esfuerzo por hacer empíricamente manejable el concepto de interdependencia industrial de Walras (1874) y se inspira en la contabilidad del diagrama del flujo circular de le tableau économique de Quesnay (1758).

Es un modelo “abierto”, en el sentido de que la decisión de qué producir (oferta) está en función de (abierta o de cara a) los que gastan o consumen (demanda final), implicando que un incremento en esta demanda tiene un efecto multiplicador en la producción. De manera que lo que se pretende determinar en el modelo es la cantidad que las diferentes industrias necesitan producir (parte endógena) para satisfacer una demanda predeterminada (parte exógena) tanto interna —para el consumo de personas, la inversión de las empresas y los gastos del Gobierno—, como externa (exportaciones netas).

El modelo, además, es estático. Por un lado, se fija la capacidad productiva o tecnológica de ese año representada por la proporción de insumos necesarios para la producción (coeficiente técnico). Es decir, una vez estimado dicho coeficiente, permanece constante, independientemente cambie la escala de la producción (rendimientos constantes de escala).

Por ende, se asume que: 1) una expansión en la industria no tiene efecto en los insumos, ignorando así las economías y des-economías de escala externas; y, 2) cada industria tiene una única tecnología productiva con la que produce solo un único bien o servicio uniforme. 

Por otro lado, se fija el acervo de capital físico (maquinaria y equipo, construcción y cambios de inventarios) en el sentido de que no se puede determinar su cambio, por lo que se considera como predeterminado (o variable exógena) en el modelo. Al ignorar los problemas de capital, se asume que no existe restricción en la capacidad productiva y por lo tanto la oferta puede responder a la demanda de forma ilimitada, perfecta, a un precio dado mayor que cero (completamente elástica), en la que los insumos no son sustitutos entre ellos.

3.2 Desarrollo algebraico del modelo¹

Para el desarrollo del álgebra matricial del modelo (Miller y Blair, 1985; Lahr y Dietzenbacher, 2001; Dietzenbacher, 1992, 2010; Dietzenbacher y Lahr, 2001; Dietzenbacher, Albino, y Kühtz, 2005; Dietzenbacher, Romero, y Bosma, 2005; Dietzenbacher, Los, Stehrer, Timmer, y de Vries, 2013; Ruiz-Mercado, 2011; Ahmad et al., 2017) en el caso de Puerto Rico, se parte de la Matriz Total de Transacciones Interindustriales T (nxn), cuyo elemento genérico simboliza la compra y venta entre las -industrias que representan el aparato productivo. En la fila se encuentra la industria i que produce y le vende el insumo que la industria j de la columna requiere para su producción. Dada posibilidad de T de separar los insumos según su origen, nos permite crear las matrices de insumo-producto local D (nxn), con su elemento genérico dij; e importada M (nxn), con su elemento genérico mij. D y M también reciben el nombre de matrices de demanda intermedia local e importada, respectivamente.

Tomando en cuenta el postulado del equilibrio general del modelo que considera que el total de oferta es igual al total de la demanda, se toma la matriz D y el vector suma de n-elementos consistentes en unos, s, para realizar la sumatoria de cada una las filas mediante su producto Ds. Luego se adiciona al vector exógeno de la demanda final por productos locales, f, (compuesto por la sumatoria de las industrias de sus componentes: personas, empresas (inversión), Gobierno y las exportaciones brutas). De modo que se obtiene el vector de y producción local o interior bruta (producción = demanda intermedia + demanda final), estableciendo la ecuación (1) como la identidad del balance material básico.

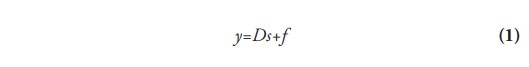
De la ecuación anterior se deduce que la demanda final resulta de la diferencia de la producción y la demanda intermedia, de manera que se despeja la ecuación (1) para f y se obtiene la equivalencia (2), que representa la segunda identidad fundamental del modelo (demanda final = producción - demanda intermedia).

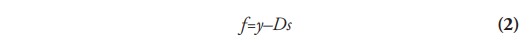
Como el interés primordial del modelo radica en determinar la producción necesaria para satisfacer la demanda final por productos locales en función de una estructura tecnológica, se tiene lógicamente que estimar primero dicha tecnología productiva en un período de tiempo específico. Para lo cual, se parte de que la producción de las industrias i (fila) está en función de la demanda de las industrias j’s (columnas) por los insumos que requiere directamente cada una para poder llevar a cabo su propia producción (yj ), incluyendo la demanda por insumos de la propia industria i cuando j = i. 

De donde se sigue que la producción de j (yj ) estará determinada por la capacidad tecnológica que tenga cada una de las industrias i’s en producir una parte (proporción) de los insumos que requiere directamente su actividad productiva (ejemplo, producción = capacidad tecnológica industrial x insumos).

Ya que tenemos la producción (vector y) y los insumos (locales e importados) que cada una de las industrias i’s proveen a la j para su producción en las matrices D y M, podemos estimar la capacidad tecnológica industrial como el cociente de cada uno de los elementos de esas matrices que resulta de su división por el vector de producción (ejemplo, capacidad tecnológica = insumos / producción). Esta razón se obtiene mediante las operaciones matriciales (3) y (4):

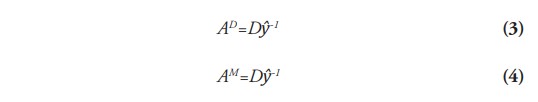
Donde AD (nxn) son AM (nxn) las matrices locales e importadas de requisitos directos por unidad de producción cuyos elementos genéricos respectivos, aij D=dij /yj y aij M=mij /yj , se denominan coeficientes técnicos y representan en cada caso una tecnología industrial determinada.

Ahora se procede a estimar la producción necesaria para hacerle frente a la demanda final con los coeficientes técnicos determinados, integrando la capacidad tecnológica local (AD) a la solución que satisface la demanda final ( f ) representada en la ecuación (1). Objetivo inmediato que se logra en tres pasos: 

Primero, se despeja la identidad (3) para D, obteniendo así la nueva identidad (5):

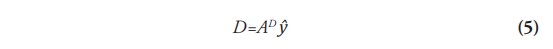
Segundo, con la identidad (5) se re-escribe la ecuación (2):

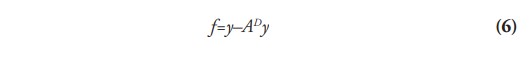
Y, tercero, la ecuación (6) se re-ordena:

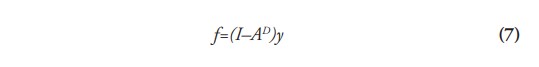
Si el rango de la matriz (I–AD)es máximo (su determinante es diferente de cero) y por lo tanto tiene inversa (sus n-filas son linealmente independientes; o, dicho de otro modo, que ninguna de sus filas sea el resultado de una combinación lineal —suma de productos por escalar— de dos o más de las demás), se puede finalmente determinar la producción (y) por medio de la ecuación (8) cuando se despeja en la ecuación (7): 

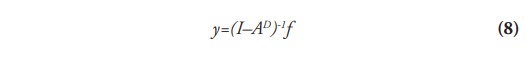
Siendo (I-AD) -1=LD (nxn) la matriz inversa de Leontief, cuyo elemento genérico l ij D representa la producción requerida de la industria i fruto de una unidad monetaria (ejemplo, un dólar) de demanda final por los productos de la industria j.

Bajo el supuesto del modelo de que la matriz de coeficientes AD no varía, se puede calcular qué vector de producción (ỹ) es requerido para satisfacer un vector específico (dado, exógeno) de demanda final (f ̃) utilizando (9): 

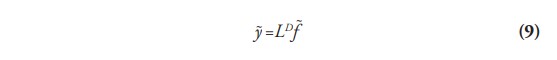
3.3 Índice de participación hacia atrás en cadenas globales de valor

Con base en la ecuación (9) se construye el índice VS, un caso especial del índice de participación hacia atrás en cadenas globales de valor de un país (Koopman et al., 2011), al considerar tres elementos:

1. La importación de insumos de productos i, requeridos para satisfacer una unidad monetaria de demanda final por el producto j; por lo que se postmultiplica la inversa de Leontief L^D por los insumos importados por unidad de producción A^M(A^ML^D).
2. El vector de exportaciones brutas de mercancías y servicios, x, como el vector exógeno de demanda final a satisfacer. Por lo que se sustituye f ̃= x.
3. La expresión del resultado en proporción de las exportaciones totales, ; por lo que se divide toda la ecuación entre la misma.

De manera que el índice queda expresado, finalmente, en la siguiente ecuación:

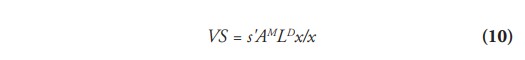
Donde es el vector suma de n-elementos consistentes en unos (1xn); A^M es la matriz (nxn) de coeficientes de insumos directos importados; L^D es la matriz inversa (nxn) de Leontief L^D=(I-A^D) ^-1, donde I es la matriz identidad (nxn) y A^D es la matriz (nxn) de coeficientes de insumos directos locales; es el vector de las exportaciones industriales; la escala de exportaciones brutas del país y el número de industrias consideradas.

Con la matriz LD postmultiplicada a la matriz AM se logra capturar, en la ecuación (10) del índice VS, el valor de los insumos importados que directa e indirectamente participaron en la producción por unidad de exportaciones ya que la matriz inversa de Leontief representa la iteración de una función de producción que a su vez está en función de otra y que por lo tanto se incluye a sí misma, en una suma geométrica que tiende al infinito (Dietzenbacher, 2010).

A partir de la ecuación (10) se derivan dos ecuaciones que capturan el valor de insumos intermedios importados que participaron directa (10a) e indirectamente (10b) en la producción de los bienes exportados: 

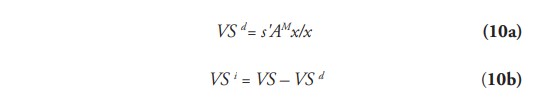
Estas ecuaciones permiten medir la contribución “con o sin los eslabonamientos locales insumo-producto” (Chen y Chang, 2006, p. 326). Es decir, si los insumos intermedios importados circulan (modo indirecto) o no (modo directo) al interior de la economía.

3.4 Eslabonamientos e industrias claves

De Rasmussen (1958) se toma su coeficiente llamado “poder de dispersión” que utiliza la matriz de Leontief (LD) , o matriz inversa de insumo, para calcular los multiplicadores de producción o la interdependencia de las industrias en insumos que sugiere el grado de eslabonamiento interindustrial hacia atrás y resulta de la siguiente ecuación matricial que indica la sumatoria de las columnas de dicha matriz:

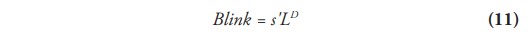
Por otro lado, la interdependencia en producción o multiplicadores de insumo, se toma de Jones (1976) al mejorar el acercamiento de Rasmussen (1958) proponiendo utilizar la matriz inversa de producción de Ghosh (1958). Así como la Inversa de Leontief se deriva de los insumos intermedios como proporción de la producción total —incluyendo el valor agregado de las cuentas sociales—; la Inversa de Ghosh se deriva de las ventas intermedias como proporción de las ventas totales, sugiriendo el grado de eslabonamiento interindustrial hacia adelante y resulta de la siguiente ecuación:

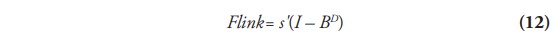
Una vez se obtienen el indicador hacia atrás y hacia adelante mediante (11) y (12), se aplica la técnica de normalización de vectores de módulo uno para comparar los valores anuales entre las industrias, de tal manera que las industrias que arrojen un resultado mayor que uno en ambos indicadores, son las industrias claves por estar por encima delw promedio.

3.5 Datos

Hasta el momento de la presente investigación, se han publicado ocho matrices totales de transacciones inter-industriales en Puerto Rico para los años fiscales 1962-63, 1966-67, 1971-72, 1976-77, 1981-82, 1986-87, 1991-92 y 2001-2002. Son elaboradas mediante censo económico y otras fuentes estadísticas cada cinco años, en la mayoría de los casos, por el Área de Planificación Económica y Social de la Junta de Planificación de Puerto Rico en coordinación con otras entidades mediante la codificación por industria del sistema de “clasificación industrial estándar” de cuatro dígitos de los Estados Unidos (SIC, por sus iniciales en inglés). En este ejercicio, se utilizan los últimos cinco (77, 82, 87, 92 y 2002) porque son las que se pueden aprovechar con la mayor desagregación sectorial comparativa posible.

A partir de ellas se construyen las MIP de Puerto Rico del tipo “no-competitivo”, es decir, la que distingue si los insumos fueron producidos localmente o importados, discriminación crucial para construir el índice de participación hacia atrás en CGV (Dietzenbacher, E., Albino, V. y Kühtz, S., 2005, p. 2; Zhang y Sun, 2012, p. 30; Koopman, R., Wang, Z. y Wei, S-J., 2012, p. 179; Dean, J., Fung, K. y Wang, Z., 2011, p. 624). Su simetría es 93x93 industrias (34 de bienes: 31 manufactura, 2 agricultura, bosque y pesca, 1 minería; 58 de servicios y 1 misceláneos), excepto la de 1977 donde la mayor desagregación posible fue de 91x91 (una industria menos tanto en manufactura como en servicios).

Los valores de las transacciones son de frecuencia anual, expresados en términos monetarios (por ejemplo, millones de dólares estadounidenses), a precios del productor. 

4. Discusión de resultados

4.1 índice de participación hacia atrás en cadenas globales de valor de Puerto Rico

Los resultados de aplicar la ecuación (10) arrojan un índice de participación hacia atrás en CGV de Puerto Rico de 41.4 % (1977), 42.5 % (1982), 35.4 % (1987), 31.3 % (1992) y 16.7 % (2002).

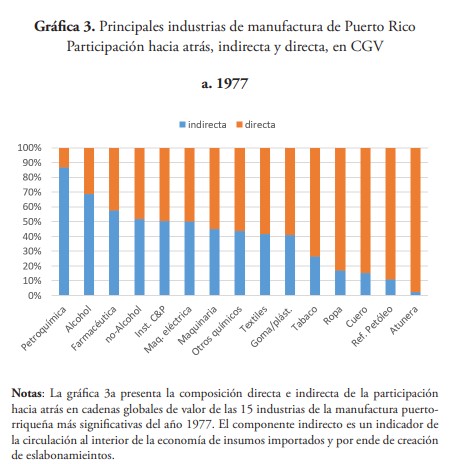
El índice ha sido mayoritariamente directo en detrimento del indirecto en los años estudiados, como resultado de aplicar la ecuación (10a) y (10b), indicando que la mayor parte de los insumos intermedios importados que son utilizados para la producción de las exportaciones en Puerto Rico, no circulan al interior de la economía, limitando así la creación de eslabonamientos con las actividades productivas (ver gráfica 1).

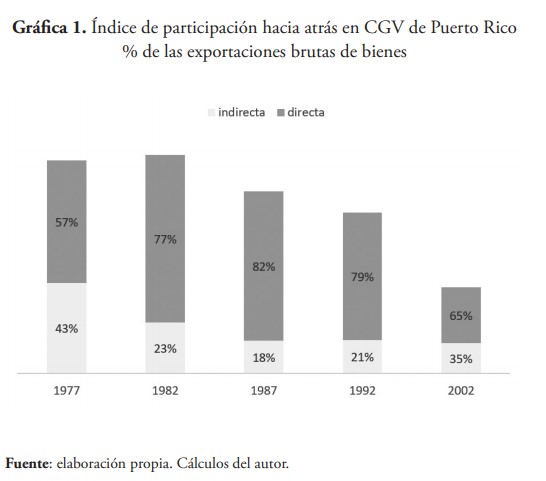
Hummels et al. (2001) encontraron caso similar en Irlanda entre 1964 y 1990, intuyendo que la presencia de multinacionales parece haber reducido la cantidad de circulación de insumos importados a través de la economía local.

Con estos cálculos del índice, si asumimos que Puerto Rico destina la totalidad de sus exportaciones a un solo país, se deberían descontar del valor de sus exportaciones brutas de bienes un promedio de 7 mil millones de dólares reales (100 = 2000) en los 5 años estudiados (5 mil millones en 1977; 8 en 1982 y 1987; 9 en 1992 y 6 en 2002), ya que se deben al denominado doble-cómputo en el hipotético caso, exclusivamente bilateral.

Por otro lado, se creó un escenario ficticio para calibrar el efecto de los insumos importados de petróleo sobre el índice, ya que la cantidad importada tiende a ser alta en los países no productores; y para aislar el efecto de la agresiva volatilidad de los precios de los mismos (Hummels et al., 2001; Amador y Cabral, 2008; Breda, Cappariello, y Zizza, 2008). El resultado fue que en 1977 el índice puertorriqueño es inflado en un 46 % por este concepto; un 29 % en 1982; un 6 % en 1987 y 1992; y, un 4 % en 2002. 

Igual ejercicio fue realizado por Hummels et al. (2001) y para 1977 encontraron que dicho impacto ronda el 30 % para Estados Unidos, Holanda y Francia; siendo el más alto en Japón, con un 67 % y el más bajo en Alemania en un 11 %.

4.2 Comparación internacional

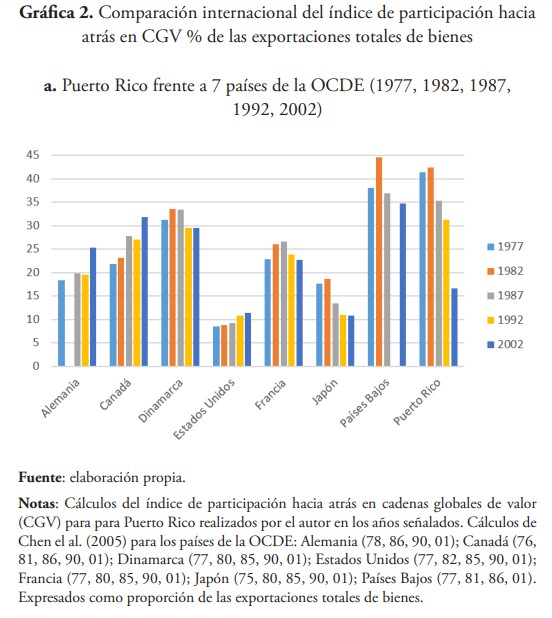
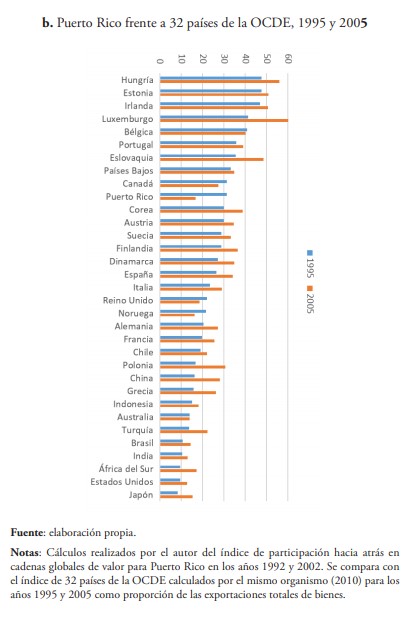
Con las muestras comparables a nivel internacional con países de la OCDE (OCDE, 2010; y Chen et al., 2005), el índice de participación hacia atrás en GVC de Puerto Rico figuró como uno de los primeros a finales de los años 70, 80 y 90 (ver gráfica 2.a y 2.b).

Sin embargo, cuando se compara el índice de los 90 con el del principio del nuevo siglo, el de Puerto Rico experimenta el mayor cambio relativo negativo de toda la muestra, al descender 15 puntos porcentuales. Solo otros tres países de los 33 considerados disminuyen su participación hacia atrás en GVC, a saber: Noruega (-5 puntos porcentuales), Canadá (-4) y Reino Unido (-3.5) (ver gráfica 2.b).

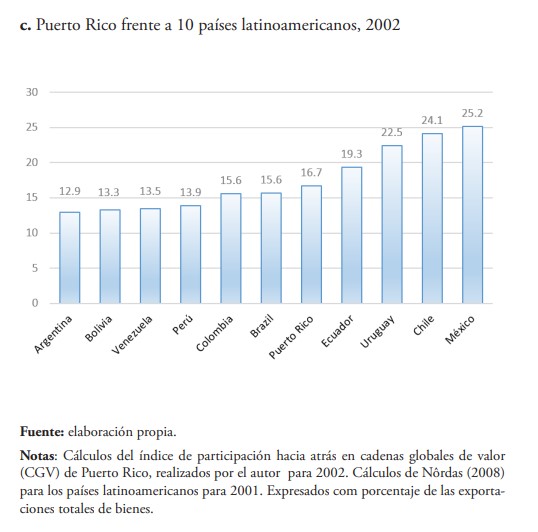
A pesar de este drástico cambio relativo, la participación hacia atrás en CGV de Puerto Rico en 2001 se sitúa prácticamente en el promedio de sus pares latinoamericanos en una muestra de 10 países calculados por Nôrdas (2008) (ver gráfica 2.c).

4.3 Participación de las industrias de manufactura de Puerto Rico

El 95 % de las industrias de Puerto Rico que en promedio participan principalmente en el esquema hacia atrás de las CGV en los años estudiados son 15 de las 31 en las que se clasifica su manufactura; y, según su composición en la suma del índice y siguiendo la clasificación de las exportaciones de Lall (2000), son encabezadas por las de alta tecnología con un promedio de 45 %, seguidas de las basadas en recursos con un 25 %, las de tecnología media (16 %) y tecnología baja (8 %) (ver tabla 3).

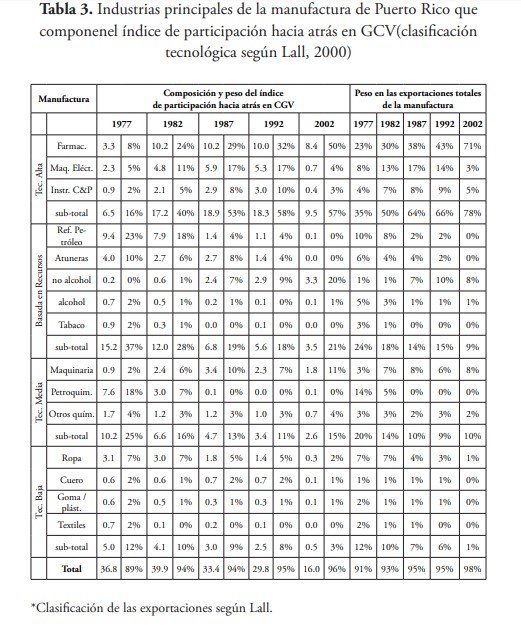
Las industrias principales de alta tecnología son las farmacéuticas, maquinarias eléctricas e instrumentos científicos y profesionales. En los tres últimos años, representan el 56 % de la participación hacia atrás en CGV. 

Las farmacéuticas lideran en todo momento, y en 2002 llega a representar el 50 % del índice total y explicar el 71 % de las exportaciones totales de la manufactura de ese año. Sin embargo, su participación en GVC es mayoritariamente directa y en ningún caso es una industria clave al aplicar las ecuaciones (11) y (12) (ver paneles gráficos 3 y 4). De hecho, ninguna industria de alta tecnología resulta serlo; solo se registran con orientación hacia adelante instrumentos C&P en 1977 y maquinaria eléctrica en 2002 (ver los paneles de las gráficas 3 y 4).

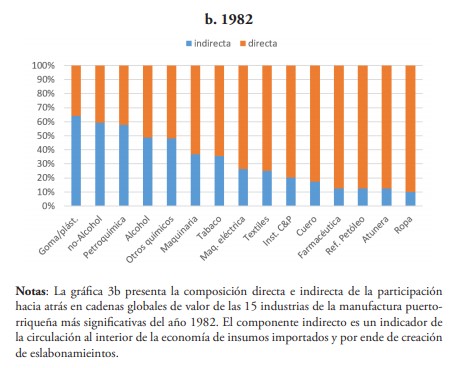
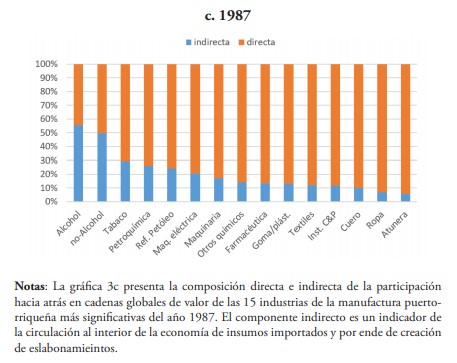
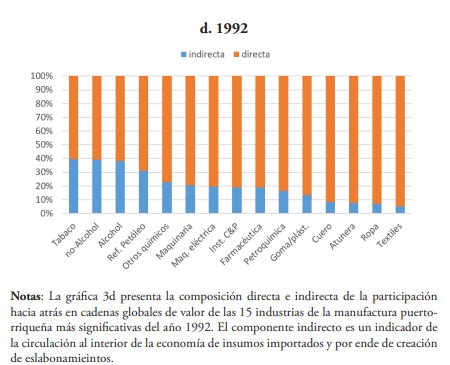
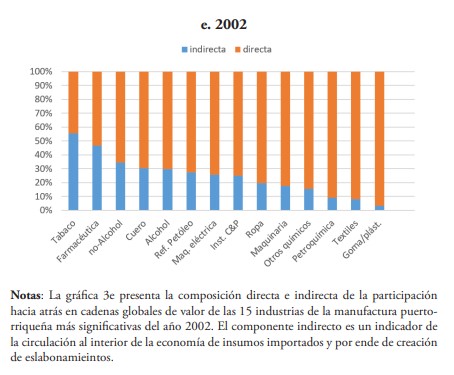
Por su parte, las industrias basadas en recursos (BR) son refinería de petróleo, pescado enlatado y curado (“atuneras”), bebidas no alcohólicas, bebidas alcohólicas y tabaco. Este último apenas participó en 1977 (2 %) y 1982 (1 %), luego, prácticamente desaparece su participación en CGV en los años siguientes estudiados. Curiosamente, los resultados muestran que en 2002 es en la única oportunidad que aparece con vínculos inter-industriales hacia atrás estando prácticamente fuera del esquema.

La refinería de petróleo, entre estas industrias BR, se destaca en 1977 y 1982, cuya participación resultó ser en un 90 % directa y explicar el 10 % y 8 % de las exportaciones. Además, se halla dentro del conjunto de industrias con vínculos hacia adelante en ambos años. Incluso, pasa a ser una industria clave en 1992 y 2002, años en que su participación hacia atrás en GVC disminuye a un 4 % y 0.3 %; lo mismo que su peso en las exportaciones a un 2 % y 0.06 %, respectivamente.

Otras industrias BR son las “atuneras” y las bebidas no-alcohólicas. En las primeras se encontró que su participación resulta ser en su totalidad prácticamente directa y en ausencia de eslabonamientos en todos los casos, indicando que pudiera tratarse del último eslabón de la cadena con la tarea de enlatado. 

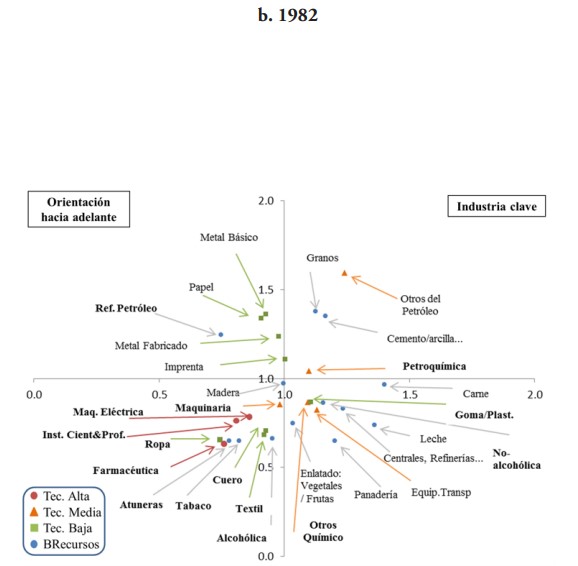
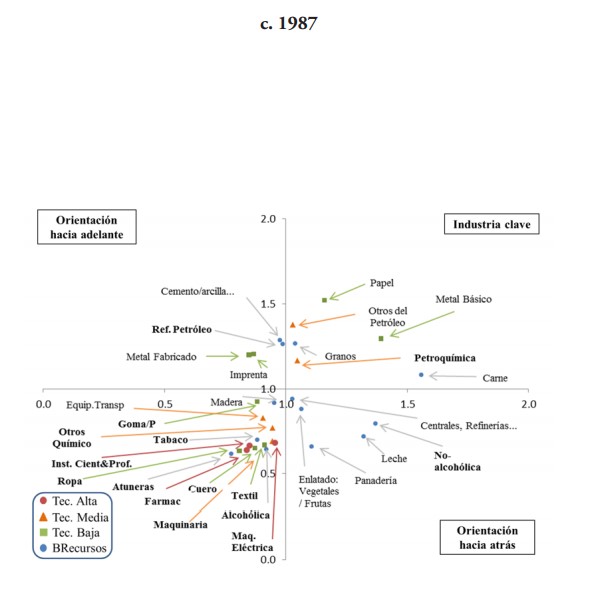
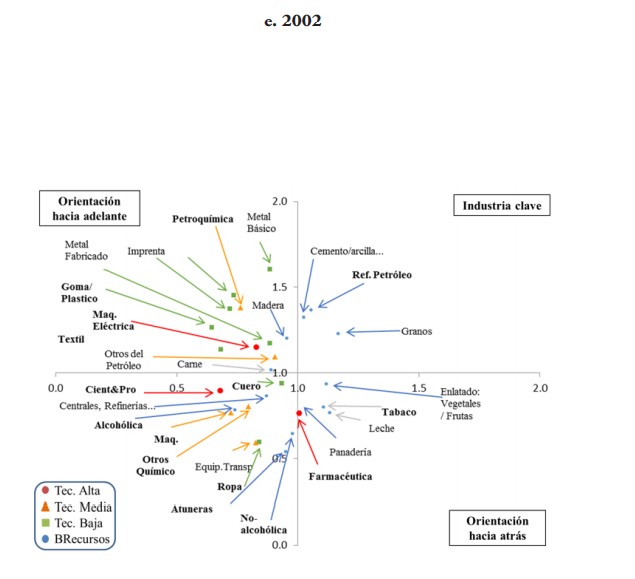
En las no-alcohólicas, los resultados reflejan una muy escasa participación en CGV en 1977 y 1982; y en un mayor porcentaje indirecta. En los años siguientes su participación relativa aumenta a un 7 % (1987), 9 % (1992) y 20 % (2002) pasando a ser directa en un 50 %, 60 % y 65 %, respectivamente. En todo caso, excepto en 2002 en que ostenta su mayor participación la segunda más grande de toda la manufactura después de las farmacéuticas, figura como una industria con vínculos hacia atrás, no así clave.

Por otro lado, las industrias de tecnología media son maquinarias, petroquímicas y otros productos químicos. Las primeras van aumentando su participación hacia atrás en GVC pasando de un 2 % en 1977 a un 11 % en 2002, en un 80 % directa en los últimos tres años y en igual período explicando en promedio el 7 % de las exportaciones. 

Las petroquímicas participan del esquema en los dos primeros años 18 % (1977) y 7 % (1982), exhibiendo un peso relativo en las exportaciones de 14 % y 5 %, respectivamente. En ambos años su participación es indirecta en un 87 % y 57 %, respectivamente. A pesar de tener este alto porcentaje, resultó ser una de las industrias claves para en ambos años y en el siguiente (1987) cuando apenas tenía un 0.22 % en el índice y explicaba el 0.18 % de las exportaciones. Luego, prácticamente sale del esquema y su peso en las exportaciones pasa a ser aún más insignificante. 

En cambio, “Otros químicos” mantiene su participación básicamente estable en todos los años, en el orden promedio del 4 %, dando cuenta del 3 % de las exportaciones. Su participación pasa de ser en un 54 % directa en promedio de los dos primeros años —en la que se halla con eslabonamientos hacia atrás— a un 82 % en los últimos tres, en la que no se encontraron vínculos inter-industriales significativos.

Finalmente, las industrias de baja tecnología son ropa y accesorios misceláneos, cuero y productos de cuero, productos de goma y plásticos y productos textiles. Los resultados muestran en ellas un descenso relativo en su participación en GVC hacia atrás de estas industrias con un 12 % en 1977, 10 % (1982), 9 % (1987), 8 % (1992) y 3 % (2002). 

La “ropa” explica, en promedio, más del 60 % de la participación de estas industrias en el esquema GVC hacia atrás, caracterizándose en ser directa en un 90 % en promedio de los cuatro primeros años. Para 2002, donde figura con el menor porcentaje de participación, es directa en un 80 %. En todo caso, carece de eslabonamientos.

De hecho, de las de baja tecnología, solo las gomas y plásticos figuran con eslabonamientos hacia atrás relativamente significativos en 1982, donde su participación en GVC hacia atrás es de un 1 %, del tipo indirecta en un 64 % y con un 1 % de las exportaciones totales. Luego, esta misma industria figura con eslabonamientos hacia adelante, en 1992 y 2002, donde se mantiene su participación relativa en GVC en 1 %, pero su peso en las exportaciones es menos del 1 % en ambos casos. En este último año, se suman los textiles con eslabonamientos hacia adelante, cuando no se quedan prácticamente fuera del esquema de GVC y su peso relativo en las exportaciones es apenas 0.03 %.

En conclusión, ninguna de las industrias que participan significativamente en la composición del índice de participación hacia atrás en GVC, resultaron ser claves en términos de creación de eslabonamientos para la economía puertorriqueña en los años estudiados, a excepción de la petroquímica en 1977 y 1982.

5. Limitaciones y futuras investigaciones

Por un lado, se pudiera ganar en profundidad analítica si se emplea la versión semi-cerrada del modelo considerando como endógeno algún componente de la demanda final o cualquier otra variable macro-económica de las cuentas nacionales (por ejemplo, valor agregado, empleo), ampliando el cuadro IP y cerrando parcialmente su solución para el componente incluido (Junta de Planificación de Puerto Rico, 1984). 

Asimismo, ante el supuesto de la estaticidad, una futura investigación pudiera incluir los modelos de equilibrio general computable (CGE, por sus iniciales en inglés) con matrices internacionales, cuyo análisis típicamente toma ciertos suministros de factores como fijos y permite que los precios se ajusten y que se asignen factores entre los sectores para lograr un nuevo equilibrio general (Walmsley, Hertel, y Hummels, 2014).

Además, el cálculo del índice no permite distinguir si los actores son empresas multinacionales o de otro tipo, en qué proporción y de qué modo participan de la CGV, entre otros detalles (OCDE, 2010). Haría falta la búsqueda de micro-datos y matrices internacionales como lo sugiere Johnson (2018) combinando distintas metodologías como lo hacen Upward, Wang, y Zheng (2012) y Dean, Lovely, y Mora, (2009) en el caso de China. De hecho, desde 2009 se han generado al menos ocho proyectos internacionales en materia de estadística con la intención de lograr este objetivo de MIP combinadas con datos del comercio internacional (Walmsley et al., 2014).

Wang, Wei, Yu, Zhu (2017) va más allá, al proponer nuevos índices de participación en CGV a partir de la descomposición total de las actividades de producción en diferentes tipos, dependiendo si son para demanda doméstica, intercambio comercial, actividades simples o complejas de CGV.

Finalmente, el supuesto de proporcionalidad del índice asume que la intensidad en el uso de los insumos importados es la misma tanto para la producción de las exportaciones como para la producción de las ventas locales (Hummels et al., 2001, p. 82). Si para la primera son utilizados de manera más intensa, entonces el índice “subestima” el grado de participación hacia atrás (Upward et al., 2012: 5). 

Esta implicación es especialmente importante ante la presencia de zonas francas de exportación donde el uso de los insumos importados es mucho mayor debido a tratamientos arancelarios preferenciales e incentivos fiscales (Koopman et al., 2012, 2011; Dean et al., 2011).  

Por consiguiente, es importante identificar explícitamente las exportaciones que responden a este régimen y crear un cuadro IP con sus coeficientes técnicos separados (Koopman et al., 2012). Lo mismo para obtener “coeficientes técnicos más puros” habría que convertir los valores de las transacciones de las matrices, al menos puertorriqueñas, de precio de productor a precio básico (Schuschny, 2005, p. 14).

6. Conclusiones

Puerto Rico exhibe entre 1977 y 1992 uno de los mayores índices relativos de participación hacia atrás en CGV cuando es comparado a nivel internacional con una muestra compatible de 39 países de la OCDE, colocándose incluso en los primeros dos lugares. En la última década analizada, experimenta la disminución relativa más grande, al caer 15 puntos porcentuales y situarse en la media de los pares latinoamericanos analizados para el 2002.

Si asumiéramos que Puerto Rico destina todas sus exportaciones a un solo país en los años estudiados, las estimaciones del índice sugieren descontar un promedio de 7 mil millones de dólares reales (100 = 2000, calculados con el deflactor implícito del PIB construido con data del Banco Mundial) por razón del “doble cómputo” en las exportaciones brutas.

Por otro lado, y en todo caso, se encontró que el contenido importado de las exportaciones ha sido mayoritariamente directo en detrimento del indirecto, lo cual confirma el análisis de industrias claves realizado, que concluye que las industrias de manufactura participantes en el esquema de las CGV hacia atrás, ha contribuido escasamente en la creación de eslabonamientos al interior de la economía que estimule su aparato productivo, salvo las petroquímicas en los dos primeros años de estudio.

8. Anexos

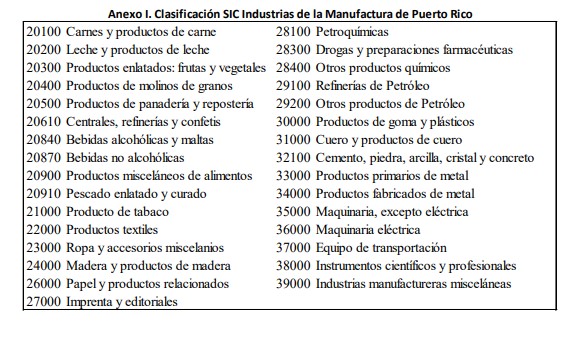
8.1) El anexo I presenta las 31 industrias de la manufactura puertorriqueña con su clasificación industrial correspondiente.

8.2) El anexo II presenta el resultado de aplicar la técnica de normalización por el promedio simple de la sumatoria de todas las industrias incluyendo los servicios a los eslabonamientos hacia atrás y hacia adelante. Sombreadas las industrias claves que en ambos eslabonamientos supera la unidad, es decir, el promedio.

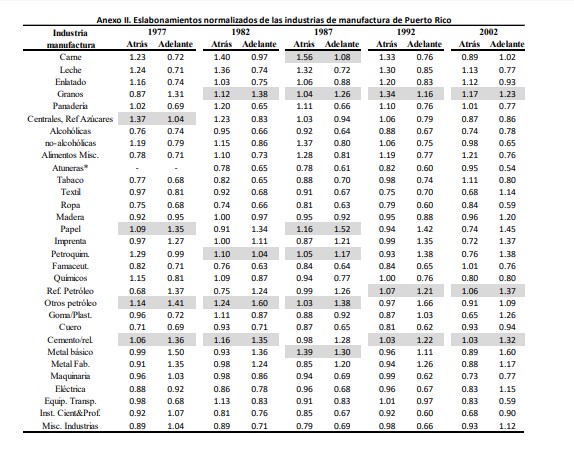
*Atuneras: en la matriz de 1977, la industria de “pescado enlatado, curado y residuos”, se encuentra asimétricamente agregada como “producto” en “productos misceláneos de alimentos”, razón por la cual no se presentan datos desagregados comparables de la misma.