Figura 1
Zonas climáticas en función del gradiente de precipitación

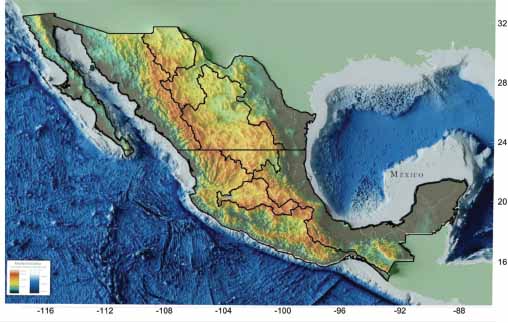
Fuente: Elaboración propia con base en CONABIO, 2007.

La Zona Intertropical de la vertiente del Golfo de México tiene 435,553.0 km², abarca toda la península de Yucatán, luego se extiende prácticamente por todo el centro norte de Chiapas, norte de Oaxaca y todo Veracruz; la Zona Intertropical de la vertiente del Océano Pacífico cuenta con 370,598.3 km², abarca desde la Sierra del, Soconusco, Chiapas, sur de Oaxaca, Guerrero, Colima, oeste de Jalisco, suroeste de Michoacán, Nayarit y la punta sur de la península de Baja California; la Zona Extratropical de la vertiente del Golfo de México cubre 279,069.4 km², abarca el estado de Tamaulipas, Nuevo León, norte de Coahuila y centro sur de Chihuahua; la Zona Extratropical de la vertiente del Océano Pacífico es de 432,195.5 km², corre desde la península de Baja California, además de Sonora y Sinaloa; en tanto el Altiplano Mexicano se compone de 442,772.8 km², y se encuentra fragmentado en tres porciones, la norte en el estado de Chihuahua, la mesa central abarca Durango, suroeste de Coahuila, noreste de Zacatecas, norte de San Luis Potosí, mientras que su porción sur abarca Guanajuato, oeste de Jalisco y norte de Michoacán. De tales regiones se intenta definir las especificidades gradiente pluviométricas, cuya metodología se explica en el siguiente apartado.

4. Datos y Metodología

La delimitación regional de estaciones meteorológicas ayudó a caracterizar los regímenes de precipitación de los gradientes pluviométricos de la República Mexicana, dicha delimitación fue discutida y justificada tanto desde el punto de vista socio-espacial propuesto por Kandziora et al. (2024) para conocer la distribución de los ecosistemas alpino tropicales en función de promedios climáticos del trimestre más frío y más cálido, como del de Mahe et al. (2001) para lograr una delimitación morfoclimática de unidades territoriales homogéneas con la intención de poder mapear y cartografiar los gradientes pluviométricos a escala nacional. En ese sentido, la propuesta analizó 3036 estaciones meteorológicas, agrupadas en cuatro zonas climáticas, a saber: Zona Intertropical de la vertiente del Golfo de México, Zona Intertropical de la vertiente del Océano Pacífico, Zona Extratropical de la vertiente del Golfo de México y Zona Extratropical de la vertiente del Océano Pacífico. (Figura 2).

Los datos concernientes a la precipitación su obtuvieron de García (2004), cuya base de datos contiene información de tres mil estaciones meteorológicas con los atributos siguientes: número de estación meteorológica, nombre de estación, Estado de la estación, altitud de la estación, longitud en grados minutos segundos, latitud en grados minutos segundos, temperatura promedio por mes, temperatura promedio anual, milímetros (mm) de precipitación por mes, milímetros (mm) de precipitación total anual, porcentaje de precipitación invernal, límites en las condiciones de temperatura o cociente (p/t)⁵, oscilación térmica y nomenclatura de tipo de clima.

Comúnmente las anomalías de precipitación suelen elaborarse tomando en cuenta un enfoque temporal, ya que en la mayoría de los estudios casi siempre se busca conocer la escasez o el superávit de la precipitación para un año determinado, sin embargo, las anomalías de precipitación de carácter espacial sirven para comprender, de un conjunto de lugares, la influencia local, tanto de los elementos geográficos (altitud) como de los factores externos del clima (circulación general de la atmosfera).

Uno de los métodos más empleados para agrupar las estaciones meteorológicas en función de su altitud, son las medidas de tendencia central, la cuales se refieren a una técnica estadística empleada para resumir en un solo valor a un conjunto de valores; los resultados pretenden evaluar en qué medida los datos del conjunto analizado son semejantes entre sí, por ejemplo, el valor medio de la muestra empleada en este trabajo (3 mil estaciones meteorológicas) se asume como numéricamente muy cercano a la realidad topográfica de la variable medida. Su expresión matemática es:

$\overline{x}=\frac{1}{n}{\displaystyle \sum _{i=1}^{n}xi}=\frac{x1+x2+\mathrm{...}+xn}{n}$

donde:

$\overline{x}$ = media o promedio.

n = suma de todos los datos recolectados (cantidad de estaciones meteorológicas).

${\displaystyle \sum {}_{i=1}}$ = sumatoria de las frecuencias (altitudes de todos los casos recolectados).

X¹ = cualquiera de los valores de n.

Ahora bien, recordemos que la moda de un conjunto de números es el valor que ocurre con mayor frecuencia, el cual se puede expresar estadísticamente de la siguiente forma:

$M=L1+\left(\frac{D1}{D1+D2}\right)C$

donde:

M = moda.

L1 = frontera inferior de la clase modal (clase que contiene a la moda).

D1 = exceso de la frecuencia modal sobre la de la clase inferior inmediata.

D2 = exceso de la frecuencia modal sobre la clase superior inmediata.

c = anchura del intervalo de clase modal.

En cuanto a la moda, se tuvieron que trazar intervalos modales para ponderar la altura para cada una de las cuatro zonas analizadas, un ejemplo se expone en el cuadro 1. De forma concomitante, los volúmenes de precipitación se interpolaron a los rangos altitudinales resultantes.

La red de estaciones meteorológicas de la zona intertropical de la vertiente del Golfo de México es de 1136, de las cuales, el 24.8% de ellas se distribuyen a lo largo del piso altitudinal de los 0 msnm; luego el 12.2% de las estaciones se corresponden con el piso de los 100 msnm; le sigue 5.6% dispuesto para el piso de los 2300 msnm; mientras que los pisos 200 y 2200 msnm cuentan cada uno con un 5.5% de estaciones meteorológicas; el resto de los 28 pisos analizados tienen una representación inferior al 4%.

La red de estaciones meteorológicas de la zona intertropical de la vertiente del Océano Pacífico es de 1096, de las cuales, el 6.8% de ellas se distribuyen a lo largo del piso altitudinal de los 0 msnm; luego el 3.9% de las estaciones se corresponden con el piso de los 100 msnm; le sigue 3.2% dispuesto para el piso de los 200 msnm; mientras que los pisos 300 y 400 msnm cuentan cada uno con un 3.0% de estaciones meteorológicas; el resto de los 29 pisos analizados tienen una representación inferior al 2.5%.

La red de estaciones meteorológicas de la zona extratropical de la vertiente del Golfo de México es de 233, de las cuales, el 15.9% de ellas se distribuyen a lo largo del piso altitudinal de los 0 msnm; luego el 9.9% de las estaciones se corresponden con el piso de los 200 msnm; le sigue 9.4% dispuesto para el piso de los 100 msnm; le sigue 9.0% dispuesto para el piso de los 300 msnm; mientras que los pisos 400 y 1200 msnm cuentan cada uno con un 7.5% de estaciones meteorológicas; el resto de los 18 pisos analizados tienen una representación inferior al 4%.

La red de estaciones meteorológicas de la zona extratropical de la vertiente del Océano Pacífico es de 574, de las cuales, el 19.1% de ellas se distribuyen a lo largo del piso altitudinal de los 0 msnm; luego el 10.3% de las estaciones se corresponden con el piso de los 100 msnm; le sigue 6.8% dispuesto para el piso de los 200 msnm; luego el piso 300 msnm cuentan con un 5.6%; entre tanto, los pisos 1900, 400, 1300, 1500 y 2000 msnm cuentan con 4.7%, 4.4%, 4.4%, 4.0% y 4.0% respectivamente, el resto de los 20 pisos analizados tienen una representación inferior al 3.5%.

Como es de apreciarse, la gran mayoría de las estaciones meteorológicas están distribuidas sobre el piso 0 y 100 del territorio, atendiendo a la lógica de un país costero tropical oceánico, cuando en realidad, hace falta que más estaciones meteorológicas se distribuyan sobre la realidad árido alpina del relieve mexicano, pues de ese modo se abonará en la comprensión del papel que juegan los elementos del clima (altitud, longitud, latitud, influencia marítima y continentalidad) en el condicionamiento local, sustancial, espacio temporal, de los regímenes altitudinales de precipitación de las distintas vertientes del territorio mexicano, tanto de las zonas intertropicales como extratropicales de las vertientes del Golfo y del Océano Pacifico, mismas que se discuten a continuación.

Figura 2
Distribución geográfica de la red nacional de estaciones meteorológicas de México

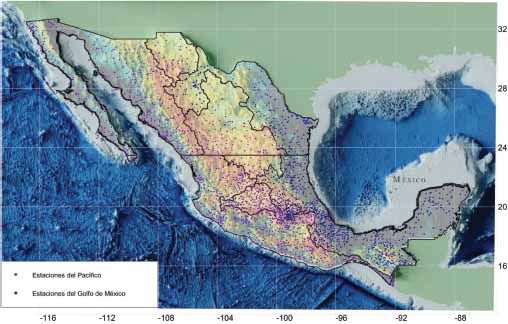
Fuente: Elaboración propia con base en García, 2004.

5. Discusión y resultados

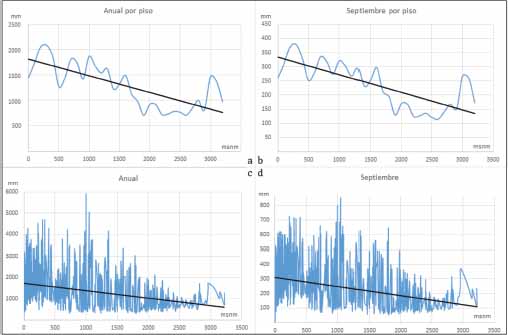
De las cuatro regiones analizadas, solo en la zona extratropical de la vertiente del Océano Pacífico, se cumple, relativamente, la definición estándar del gradiente pluviométrico, puesto que: a medida que se asciende en altitud, estadísticamente, la cantidad de precipitación, conforme a la línea de tendencia, tiende a aumentar pasando por cuatro óptimos ubicados: a los 650, 1500⁶, 2000 y 2600 msnm con 1400, 2200, 1470 y 1550 mm respectivamente (Gráfica 1a y 1c). Las características altitudinales de dicho gradiente pluviométrico son influenciadas por factores como la elevación de las montañas, la relativa proximidad al mar y la evotranspiración de los parches boscosos de coníferas.

Gráfica 1
Gradiente pluviométrico la zona extratropical de la vertiente del Océano Pacífico

Fuente: elaboración propia con base en García (2004).

Esa progresión o aumento de la precipitación con la altura, que experimenta la zona extratropical de la vertiente del Océano Pacífico, también se aprecia en el mes más lluvioso del año, septiembre (Gráfica 1b y 1d), el cual presenta cinco picos óptimos, tres de los cuales superan los 250 mm, como en el caso de: los 650, 1875 y 2570 msnm, con 301, 252 y 312 mm respectivamente. Donde, geoestadísticamente, su línea de tendencia sugiere que, por cada 100 m de ascenso, en septiembre, el gradiente pluviométrico gana 11.5 mm de lluvia, en tanto que anualmente la ganancia es de 81.7 mm por 100 de altitud.

Ahora bien, en la zona intertropical de la vertiente del Océano Pacífico, no se cumple con un gradiente pluviométrico ascendente, puesto que: a medida que se asciende en altitud, estadísticamente, la cantidad de precipitación, conforme a la línea de tendencia, tiende a disminuir (Gráfica 2b), de hecho, el análisis modal arroja solo dos óptimos pluviométrico ubicados: a los 600 y 3100 msnm con 1780 y 1450 mm de lluvia anual respectivamente (Gráfica 2a).

Gráfica 2
Gradiente pluviométrico la zona intertropical de la vertiente del Océano Pacífico

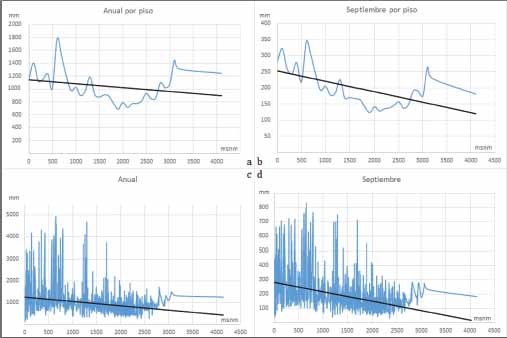
Fuente: elaboración propia con base en García (2004).

Ese decremento o cuña descendente de la precipitación conforme a su altitud, que experimenta la zona intertropical de la vertiente del Océano Pacífico, también se aprecia en el mes de septiembre, ya que, conforme a su análisis modal (Gráfica 2b), éste, presenta los mismos dos óptimos pluviométrico, a los 600 y 3100 msnm con 344 y 264 mm de lluvia mensual respectivamente. Donde, geoestadísticamente, de sus 600 a sus 2000 msnm, su gradiente pluviométrico anual por cada 100 m de ascenso pierde 127 mm, luego de allí, de los 2000 a sus 3100 msnm tal gradiente por cada 100 m de ascenso gana 130 mm. En efecto, la forma geométrica de dicho gradiente se asemeja a una parábola cuyo vértice se ubica a los 1900 msnm (Gráfica 2a y 2b).

Para el caso del Atlántico, en la zona extratropical de la vertiente del Golfo de México, conforme a la línea de tendencia, se presenta un ligerísimo gradiente pluviométrico (Gráfica 3a), que va de sus 700 a sus 1900 msnm, donde por cada 100 m de ascenso solo gana 31 mm. Más bien esta zona presenta dos pisos pluviométricos: el primero de ellos presenta una media de precipitación de 650 mm para las altitudes de 0 a 600 msnm; el segundo piso tiene una precipitación de 300 mm para las altitudes de 650 a 1500 msnm; imbricado en ello están tres óptimos pluviométricos: a los 45, 200 y 1100 msnm con 1950, 1970 y 1480 mm respectivamente (Gráfica 3c).

Gráfica 3
Gradiente pluviométrico la zona extratropical de la vertiente del Golfo de México

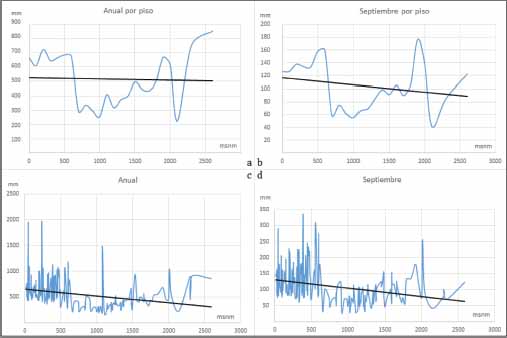
Fuente: elaboración propia con base en García (2004).

Tal configuración pluviométrica es más marcada en el gráfico de septiembre, donde se distinguen claramente los dos pisos (Gráfica 3b), el ligero gradiente y cuatro picos óptimos. El primer piso tiene una precipitación media de 140 mm para las altitudes de 0 a 600 msnm, el siguiente piso es de 66 mm de los 650 a los 1100 msnm, de allí inicia el ligero gradiente pluviométrico y culmina hasta los 1800 msnm, donde por cada 100 m de ascenso gana 23 mm. Siendo los óptimos pluviométricos para septiembre: a los 45, 385, 600 y 2100 msnm con 290, 335, 290 y 255 mm respectivamente (Gráfica 3d).

Ahora bien, en la zona intertropical de la vertiente del Golfo de México, no se cumple con un gradiente pluviométrico ascendente, ya que: a medida que se asciende en altitud, estadísticamente, la cantidad de precipitación, conforme a la línea de tendencia, tiende a disminuir, de hecho, el análisis modal (Gráfica 4a) presenta un solo óptimo pluviométrico bien definido a los 1000 msnm con 5876 mm de precipitación anual.

Gráfica 4
Gradiente pluviométrico la zona intertropical de la vertiente del Golfo de México

Fuente: elaboración propia con base en García (2004).

Geoestadísticamente, su gradiente pluviométrico anual por cada 100 m de ascenso pierde 182 mm (Gráfica 4c). Las características somero altitudinales tanto de la península de Yucatán, como de la amplia llanura costera del golfo, más la proximidad al mar y la evotranspiración de la selva alta perennifolia, hacen que este gradiente pluviométrico se comporte como el de una región costera tropical oceánica, semejante al de Hawái o Panamá (Anders y Nesbitt, 2015; Condit et al., 2004).

La cuña descendente descrita, que experimenta la zona intertropical de la vertiente del Golfo de México, se aprecia con mayor claridad en el mes de septiembre (Gráfica 4b), ya que presenta un único óptimo pluviométrico, distinguible a los 1050 msnm con 844 mm de lluvia mensual. Es útil señalar que su gradiente pluviométrico mensual por cada 100 m de ascenso pierde 26.2 mm.

6. Conclusiones

En México, el comportamiento de las lluvias tiene múltiples características, sin embargo, a escala macro regional, se pueden diferenciar cuatro gradientes pluviométricos, con especificidades claramente diferenciables, por ejemplo: en la zona extratropical de la vertiente del Océano Pacífico se experimenta una progresión o aumento de la precipitación con la altura a razón de 80 mm por 100 de altitud aproximadamente. Es útil señalar que esta región es la única cuyo gradiente se parece al de las zonas templadas del mundo.

Las otras tres regiones tienen puntualizaciones siu generis, como en el caso de la zona intertropical de la vertiente del Océano Pacífico y la zona intertropical de la vertiente del Golfo de México, donde a medida que se asciende en altitud, la cantidad de precipitación tiende a disminuir, siendo muchísimo más pronunciado y marcado el fenómeno en ésta última.

Es decir, en la vertiente intertropical de la vertiente del Océano Pacífico por cada 100 m de ascenso se pierden 127 mm, mientras que en la vertiente del Golfo de México por cada 100 m de ascenso se pierden 182 mm. Bajo lo expuesto, se sabe que las precipitaciones anuales en las montañas de la vertiente del Golfo de México, situadas por arriba de los 1 800 msnm, en promedio, son ligeramente 50 mm mayores en comparación con la vertiente del Pacífico.

Finalmente, en la vertiente extratropical del Golfo de México se presentas dos pisos pluviométricos: el primero de ellos presenta una media de precipitación de 650 mm para las altitudes de 0 a 600 msnm; el segundo piso tiene una precipitación de 300 mm para las altitudes de 650 a 1500 msnm. En contexto, se infiere que las precipitaciones anuales en las montañas situadas por arriba de los 1 800 msnm e inmersas en el gradiente intratropical de la vertiente del Golfo de México, en promedio, son 200 mm mayores en comparación con las de la vertiente del Pacífico.

Al respecto, si bien es cierto que los patrones de precipitación son complejos y a veces hasta impredecibles, la tipificación expuesta abona a la comprensión regional de la dinámica pluviométrica y climatológica de un país trópico intermontano, con fuertes efectos de continentalidad al norte y marcados efectos de maritimidad al sur, de gran utilidad para simulaciones o escenarios futuros bajo condiciones de cambio climático acelerado.

Referencias

Anders, A. M., y Nesbitt, S. W. (2015). Altitudinal precipitation gradients in the tropics from Tropical Rainfall Measuring Mission (TRMM) precipitation radar. Journal of Hydrometeorology, 16(1), 441-448.

Andrade, M., y Medrano, O. R. (2021). Historical precipitation patterns in the South-Southeast region of Mexico and future projections. Earth Sciences Research Journal, 25(1), 69-84.

Ceballos, A., Martínez-Fernández, J., y Luengo-Ugidos, M. Á. (2004). Analysis of rainfall trends and dry periods on a pluviometric gradient representative of Mediterranean climate in the Duero Basin, Spain. Journal of Arid Environments, 58(2), 215-233.

CONABIO. (2007). Cuencas Hidrográficas de México. México: Comisión Nacional para el Conocimiento y Uso de la Biodiversidad. http://geoportal.conabio.gob.mx/metadatos/doc/html/cue250k_07gw.html

Condit, R., Aguilar, S., Hernandez, A., Perez, R., Lao, S., Angehr, G.,... y Foster, R. B. (2004). Tropical forest dynamics across a rainfall gradient and the impact of an El Nino dry season. Journal of Tropical Ecology, 20(1), 51-72.

Del Valle, J. y San Roman, J. (1994). Gradiente pluviométrico en el macizo del Moncayo (Zaragoza y Soria). Geographicalia, 31, 71-82.

Douguédroit, A., y De Saintignon, M. F. (1984). Les gradients de températures et de précipitations en montagne. Revue de géographie alpine, 72(2), 225-240.

García, Enriqueta (2004). Modificaciones al sistema de clasificación climática de Köppen (para adaptarlo a las condiciones de la República Mexicana). México: Instituto de Geografía, Universidad Nacional Autónoma de México.

INEGI. (2017). Anuario estadístico y geográfico de los Estados Unidos Mexicanos. Aguascalientes, México: Instituto Nacional de Estadística y Geografía.

Kandziora, M., Gorospe, J. M., Salomon, L., Vásquez, D. L., Vargas, M. P., Kolář, F., ... y Schmickl, R. (2024). The ghost of past climate acting on present‐day plant diversity: Lessons from a climate‐based delimitation of the tropical alpine ecosystem. Journal of Systematics and Evolution, 62(2), 275-290.

Li, G., Yu, Z., Wang, W., Ju, Q., & Chen, X. (2021). Analysis of the spatial Distribution of precipitation and topography with GPM data in the Tibetan Plateau. Atmospheric Research, 247, 105259.

Mahe, G. I. L., L’hote, Y., Olivry, J. C., y Wotling, G. (2001). Trends and discontinuities in regional rainfall of West and Central Africa: 1951–1989. Hydrological sciences journal, 46(2), 211-226.

Mandujano, S., y Naranjo, E. J. (2010). Ungulate biomass across a rainfall gradient: a comparison of data from Neotropical and Palaeotropical forests and local analyses in Mexico. Journal of Tropical Ecology, 26(1), 13-23.

Méndez, J., Návar, J. D. J., y González, V. (2008). Análisis de tendencias de precipitación (1920-2004) en México. Investigaciones geográficas, 65, 38-55.

Muñoz, P., Célleri, R., y Feyen, J. (2016). Effect of the resolution of tipping-bucket rain gauge and calculation method on rainfall intensities in an Andean mountain gradient. Water, 8(11), 534.

Nazarian, R. H., Brizuela, N. G., Matijevic, B. J., Vizzard, J. V., Agostino, C. P., y Lutsko, N. J. (2024). Projected Changes in Mean and Extreme Precipitation Over Northern Mexico. Journal of Climate, 37, 2405 – 2422.

Niessner, A., Küppers, M., Graham, J., Valenzuela, L., Güney, A., Remmele, S., y Zimmermann, R. (2020). Climate and seasonal rainfall anomalies along an elevational gradient in the El Sira Mountains, Peru, and their impacts on tree radial growth. Journal of forestry research, 31, 1521-1538.

Ruiz Sinoga, J. D., Garcia Marín, R., Martínez‐Murillo, J. F., y Gabarrón Galeote, M. A. (2010). Pluviometric gradient incidence and the hydrological behaviour of soil surface components (southern Spain). Land degradation & development, 21(5), 484-495.

Slimani, M., Cudennec, C., y Feki, H. (2007). Structure du gradient pluviométrique de la transition Méditerranée–Sahara en Tunisie: déterminants géographiques et saisonnalité. Journal des Sciences Hydrologiques, 52(6), 1088-1102.

Tovar, R., Vargas, R., y Rueda, J. (2022). “Cambio climático y perspectivas agroalimentarias en el noroeste de México” en: Olivera, M. y Gustavo Sosa (Coords). Impactos del cambio climático: una visión desde México. México: Universidad Autónoma Metropolitana–Unidad Cuajimalpa, Instituto de Investigaciones Dr. José María Luis Mora. (pp 95-116).

Urdiales, D., y Célleri, R. (2018). Pronóstico de la ocurrencia de precipitación diaria en un gradiente altitudinal en el Sur del Ecuador mediante un generador climático. Enfoque UTE, 9(3), 29-41.

Yang, Y., Fang, J., Fay, P. A., Bell, J. E., y Ji, C. (2010). Rain use efficiency across a precipitation gradient on the Tibetan Plateau. Geophysical Research Letters, 37(15).

_______________________________

¹ El Colegio de Veracruz. ORCID: 0000-0003-4873-2502. Correo-e: rod_geo77@hotmail.com

² Universidad Autónoma de Nuevo León, Instituto de Investigaciones Sociales. ORCID: 0000-0003-0319-6777

³ Universidad Autónoma de Tamaulipas: Tampico, Tamaulipas, Mexico. ORCID: 0000-0002-2447-5356

⁴ Las precipitaciones aumentan con la altitud hasta llegar a la cota óptima pluvial u óptimo pluviométrico, a partir del cual se registran precipitaciones menores, esto se aprecia claramente en regiones con alturas superiores a los 2000 msnm.

⁵ El P/T, también conocido como índice de Lang es un estimador de eficiencia de la precipitación en relación con la temperatura. Éste se calcula como el cociente entre la precipitación total anual y la temperatura media anual de un lugar.

⁶ Altitud sobre la que se encuentra aproximadamente la presa Las Lajas (1540 msnm) en el municipio de Buenaventura Chihuahua.