MODELOS DE PREDICCIÓN DEL IMPACTO Y EVOLUCIÓN DEL COVID-19 EN REPÚBLICA DOMINICANA

Introducción

En el último trimestre del año 2019, en la ciudad de Wuhan, provincia de Hubei, China, fueron reportados un gran número de casos de afecciones respiratorias de las vías inferiores, que hasta ese momento eran de origen idiopático. En muchos de los pacientes, estas afecciones estaban causando un cuadro clínico caracterizado por una dificultad respiratoria aguda, similar al síndrome respiratorio agudo severo (SARS). A partir de estudios de secuenciación de nueva generación de muestras obtenidas de pacientes chinos, se demostró que se trataba de un nuevo coronavirus, designado como SARS-CoV-2, que es el factor causal de la enfermedad COVID-19 (Wang, Horby, Hayden, & Gao, 2020; Zhu et al., 2020).

El virus pudo tener un origen zoonótico (Andersen, Rambaut, Lipkin, Holmes, & Garry, 2020), debido a que muchos de los primeros casos de pacientes reportados en China estaban relacionados al mercado mojado de Huana, donde existe la comercialización de diferentes tipos de animales silvestres (Hui et al., 2020; Zhou et al., 2020). El SARS-CoV-2 presenta una alta similitud con otros coronavirus como el SARS-CoV, identificado en China en 2002, causante del síndrome respiratorio agudo grave (SARS). Algunas hipótesis sugieren que el murciélago (Rhinolophus affinis) es el reservorio progenitor, debido a que el virus RaTG13 muestreado en este quiróptero, presentó una similitud de ∼96 % con el virus del SARS-CoV-2 (Zhou et al., 2020). Otra hipótesis sugiere que el virus pudiera tener a los pangolines de Malasia (Manis javanica) como organismos reservorios del virus, debido a que se han identificados coronavirus similares al SARS-CoV-2, en animales de esta especie vendidos en los mercados de China (Forster, Forster, Renfrew, & Forster, 2020; Wu et al., 2020). 

El COVID-19 es la enfermedad infecciosa causada por el SARS-CoV-2, esta se caracteriza por síntomas clínicos como fiebre, tos seca y fatiga. También se han descritos casos de pacientes que relatan dolor muscular, dolor de cabeza o confusión, dolor abdominal, náuseas, vómitos y diarrea. Entre los casos más severos de pacientes que han sido hospitalizados, se han observado linfógena, hipercitoquinemia, coagulación intravasal diseminada y daño renal agudo (Chan et al., 2020; Chen et al., 2020; Huang et al., 2020; Wang et al., 2020). Los pacientes que desarrollan el síndrome respiratorio agudo tienen un cuadro clínico grave, que tiende a empeorar en un periodo corto de tiempo, provocando la muerte por insuficiencia orgánica múltiple (Tang, Wang et al., 2020; Zhao, Lin et al., 2020).

En la actualidad el virus se ha extendido a más de 100 países en todo el mundo, con una tasa de contagio (R₀) estimada entre 1.5 y 6.8 (Liu, Gayle, Wilder-Smith, & Rocklöv, 2020; Viceconte & Petrosillo, 2020; WHO, 2020b), provocando ∼3,000,000 de personas infectadas y ∼233,792 a nivel mundial al 30 de abril de 2020 (Dong, Du, & Gardner, 2020). Reportes han informado que la tasa de letalidad de los pacientes hospitalizado está entre 2.3 % y 11.5 % (Chen et al., 2020), tasa que varía de país a país y depende de la infraestructura sanitaria disponible para la atención de los pacientes con esta enfermedad (Zhao, Musa et al., 2020).

En la República Dominicana, el primer caso de COVID-19 fue confirmado el primero de marzo de 2020, un paciente masculino de 62 años de edad, de nacionalidad italiana, quien habría ingresado al país nueve días antes (Organización Panamericana de la Salud, 2020). Desde esa fecha comenzó el proceso de expansión del agente infeccioso dentro de país, situación que obligó a las autoridades a tomar medidas con la finalidad de contener la propagación de virus. En la actualidad, el país está entre la lista de los más afectado en América Latina y ocupa el puesto número seis en la región (Rios Montanez, 2020) y el número 43 a nivel mundial (datos al 29/04/2020) (Dong et al., 2020), en relación con la cantidad de infectados que han sido confirmados. El país reporta a finales de abril de 2020 que había sobrepasado los 6,500 infectados y los 300 muertos por causa de la enfermedad, número que puede ser mayor debido a los casos asintomáticos que no son reportados y la cantidad limitada de pruebas que han sido realizadas.

Diversos esfuerzos están siendo realizados por la comunidad científica con la intención de modelar y predecir la evolución y el impacto de la pandemia en los diferentes países y regiones (Amira et al., 2020; Sanche et al., 2020; Tang, Bragazzi et al., 2020; Tang, Wang et al., 2020; Zhao, Musa et al., 2020). Una de las herramientas que puede ayudar en esta tarea son los modelos matemáticos y computacionales, que permiten generar proyecciones de los diferentes escenarios de la pandemia, lo que puede ayudar en la planificación de las acciones, recursos e infraestructuras; además, permiten probar diferentes hipótesis, y el descarte de soluciones poco realistas, o muy optimistas.

La Organización Mundial de la Salud (OMS), ha reconocido que los modelos matemáticos, estadísticos y computacionales pueden desempeñar un papel clave para proporcionar información, basada en evidencias, a los responsables de tomar decisiones en materia de políticas de salud públicas. Estos modelos pueden ayudar a comprender qué tan transmisible es la enfermedad; cuándo serán más altas las tasas de infecciones; qué tan grave es la infección y qué tan efectivas han sido las intervenciones (Tang, Bragazzi, et al., 2020).

En la actualidad, diversos modelos son usados para comprender las enfermedades infecciosas, como el modelo Susceptible-Infectious-Recovered (SIR) (Kermack & McKendrick, 1927; Lin, Muthuraman, & Lawley, 2010), utilizado para modelar enfermedades infecciosas que se propagan a través de gotitas y aerosoles como la gripe pandémica (Bootsma & Ferguson, 2007), la gripe estacional (Markel et al., 2006), el SARS (Riley et al., 2003), y la viruela (Riley & Ferguson, 2006) y pueden ayudar a entender la expansión y propagación del COVID-19 (Bastos & Cajueiro, 2020). Otro método para el análisis de las epidemias es el Susceptible-Exposed-Infectious-Recovered (SEIR) (Li, Graef, Wang, & Karsai, 1999), este es un modelo dinámico que permite estudiar las enfermedades contagiosas teniendo en cuenta factores comportamentales de las poblaciones, este modelo permite simular los procesos de infección desde la fuente, los huéspedes, los reservorios y la transmisión a los humanos (De La Sen & Alonso-Quesada, 2011; Liu & Zhang, 2011). Además de adicionar variables de temporalidad como son el período de incubación de la enfermedad y los efectos de las medidas de contención. Este modelo ya ha sido utilizado en enfermedades infecciosas como el SARS, MERS y el COVID-19 (Peng, Yang, Zhang, Zhuge, & Hong, 2020; Rao, Keshri, Mishra, & Panda, 2020).

El presente trabajo explora la construcción y aplicación de los modelos matemáticos SIR, SEIR y log-lineal con la finalidad de analizar y predecir el desarrollo y la evolución del SARS-CoV-2 en la República Dominicana. La adaptación de estos modelos al contexto dominicano, posibilitan explorar los índices de crecimiento del virus, la tasa de contagio y mortalidad, además de la predicción de diferentes escenarios sobre el final de la pandemia, a través de los datos oficiales disponibles hasta el 30 de abril del 2020.

Materiales y métodos

Modelo Susceptible-Infectious-Recovered (SIR)

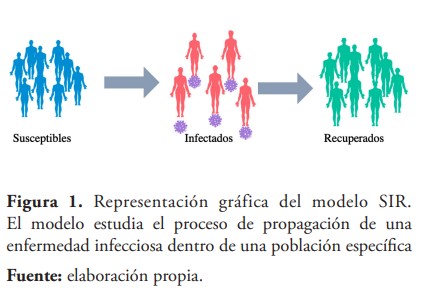
Este modelo matemático posibilita estudiar las epidemias a través de la identificación de diferentes variables independientes y dependientes, estas ayudan a determinar los parámetros óptimos que permiten que el modelo se ajuste a los datos. El modelo estudia el flujo (figura 1) de las personas entre cuatro posibles estados, durante el brote de la enfermedad: Susceptible (S), Expuesto y Resistente (R) (Britton & Pardoux, 2019), para esto utiliza las siguiente ecuación diferencial:

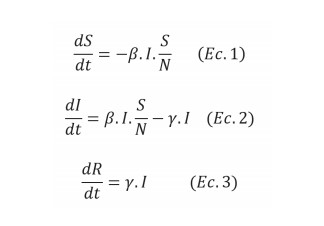
Donde, N es la población total de la zona geográfica que está siendo estudiada; S(t), es el número de persona susceptibles en un día; I(t) número de personas infectadas en el día; R(t) número de personas recuperadas en el día; b, es la cantidad de personas esperadas que una persona infectada puede infectar por día; d, es el número de días que una persona infectada tiene y puede transmitir la enfermedad; g, la proporción de infectados que se recuperan por día (g = 1/d) y R₀ es el número total de personas que contagia una persona infectada (R₀ = b/g).

La primera ecuación (Ec.1) establece que el número de individuos susceptibles (S) disminuye con el número de nuevos individuos recién infectados; la ecuación 2 (Ec.2) establece el número de individuos infecciosos (I) que aumenta con los individuos recién infectados, y la ecuación 3 (Ec.3) establece que el grupo de individuos recuperados (R) aumenta con el número de individuos que fueron infectados y que se recuperaron o murieron (Britton & Pardoux, 2019; Soetewey, 2020). 

Para implementar este modelo se usó el programa estadístico R (Free Software Foundation, 2016), basado en un método presentado por von Jouanne-Diedrich (2019) que realizó un análisis de los casos de COVID-19 en Alemania. Los códigos y datos fueron adaptados al contexto de la República Dominicana.

Modelo SIR extendido (SEIR-E)

Este modelo es una evolución del modelo SIR que incluye la exposición al patógeno como un nuevo estado dentro del modelo. Un individuo expuesto, es un individuo perteneciente al grupo de los susceptibles, que fue expuesto al virus, pero que todavía no puede transmitir la enfermedad. Este modelo también agrega dos variables: Muertos (D) y Recuperados (R), que son los estados a los que puede pasar una persona infectada después de varios días con la enfermedad (figura 2). Este modelo también permite el análisis de las personas que están en estado crítico, es decir, aquellos que van a necesitar de cuidados intensivos, así como la cantidad de camas en las unidades de cuidados intensivos (UCI) disponibles en el sistema de salud. El analizar estos números es de vital importancia para predecir las infraestructuras y cantidad de recursos sanitarios y de salud que serán necesarios para mitigar los efectos de la enfermedad (Amira et al., 2020; Li et al., 1999; J. Liu & Zhang, 2011; Van Den Driessche, 2008). 

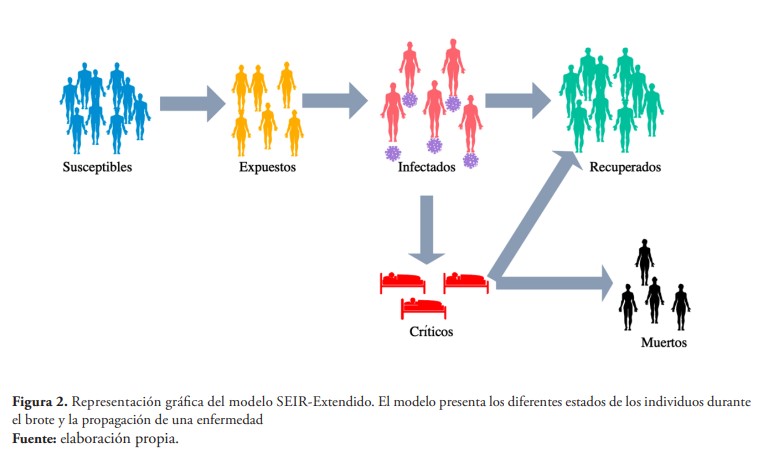
Este modelo es representado por las siguientes ecuaciones:

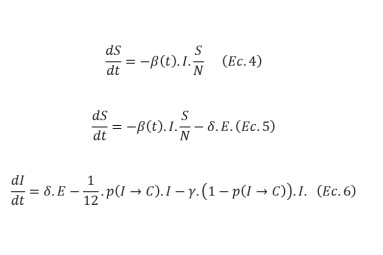
donde, N es la población total de la zona geográfica que está siendo estudiada; S(t), es el número de persona susceptibles en un día; I(t) número de personas infectadas en el día; R(t) número de personas recuperadas en el día; D(t) número de personas fallecidas por días; b, es la cantidad de personas esperadas que una persona infectada puede contagiar por día; D, es el número de días que una persona infectada tiene y puede transmitir la enfermedad; g, la proporción de individuos que se que recuperan por día (g = 1/D); R₀ , es el número total de personas que puede contagiar una persona infectada (R₀ = b/g); d, corresponde a la duración del período de incubación de la enfermedad; a, representa la tasa de mortalidad; r, es la tasa a la que mueren los individuos (=1/días desde la infección hasta la muerte); C, representa la cantidad de individuos que necesitan cuidados intensivos; probabilidad de pasar de infectado a crítico y probabilidad de pasar de estado crítico a muerte (Froese, 2020; Van Den Driessche, 2008).

Basados en los informes y estadísticas actuales del COVID-19, fue estimado en 12 días (1/12), el parámetro en 7.5 días (1/7.5), y el número de días de un individuo para pasar de crítico a recuperado fue estimado en 6.5 (1/6.5) (Chen et al., 2020; Li et al., 2020; Wang et al., 2020; WHO, 2020a). Para implementar el modelo fue adaptado el método presentado por Froese (2020) utilizando el lenguaje de programación Python y Jupyter-notebook.

Modelo log-lineal

En la fase inicial del brote de una enfermedad, cuando se analizan los primeros casos y se representan en un gráfico; estos muestran una tendencia logarítmica lineal (el eje y es una escala logarítmica y el eje x sin transformación), lo permite que los datos pueden ser ajustados a una recta de la forma mx+b. Esta representación sugiere que pueden ser usados modelos log-lineal para modelar el crecimiento y el avance de la epidemia (Churches, 2020; Soetewey, 2020). Los modelos log-lineal, son modelos matemáticos que toman la forma de una función cuyo logaritmo es igual a una combinación lineal de los parámetros del modelo, esto permite que se puedan aplicar modelos de regresión lineal (Chung et al., 2016; Greenland, 1989).

El modelo lineal simple puede ser representado por la siguiente ecuación:

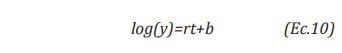
Donde, y es la incidencia, r es la tasa de crecimiento, t es el número de días desde un punto específico en el tiempo y b es la intercesión. Este modelo puede ser usado en el contexto del COVID-19 para generar dos modelos: 1) la fase de crecimiento (antes del pico); 2) la fase de descomposición (después del pico), que se ajustan a la curva de la epidemia (caso de incidencia) (Soetewey, 2020).

Para la implementación de este modelo fue utilizado el lenguaje estadístico R (Free Software Foundation, 2016). Para el modelado y ajustes de la curva fue utilizado el paquete incidence (Kamvar, Cai, Pulliam, Schumacher, & Jombart, 2019) que forma parte del conjunto de paquetes de R Epidemic Consortium (RECON).

Obtención de los datos

Para la implementación de los modelos se recolectaron datos sobre el estado actual del COVID-19 en República Dominicana, a través de diferentes fuentes. El conjunto de datos con la cantidad de casos confirmados, números de muertos, nuevos casos diarios y cantidad de recuperados fueron obtenidos de los reportes sobre el virus, publicados diariamente por el Ministerio de Salud Pública de la República Dominicana (Ministerio de Salud Pública de República Dominicana, 2020) y de la base de datos de los casos globales de COVID-19 (Johns Hopkins University, 2020). Para generar los modelos de análisis, fue seleccionado un periodo de tiempo que comprende 60 días, desde el 1 de marzo 2020 (primer caso confirmado) hasta el 30 de abril de 2020. Los datos fueron obtenidos el día 30 de abril de 2020.

El dato sobre la población total estimada de República Dominicana (10, 448,499) fue obtenido del informe de estimaciones y proyecciones de población total de la Oficina Nacional de Estadística de la República Dominicana (ONE) (2020) y los datos sobre la distribución de la pirámide poblacional estimada para República Dominicana, fueron tomados de Population Pyramid, (2019).

Los datos sobre la cantidad de camas disponibles fueron obtenidos de la Organizacion de las Naciones Unidas (ONU) (2020), para obtener la cantidad de cama en las UCIs, se hizo una estimación, utilizando el promedio camas disponibles en otros países de América Latina que presentan un índice de desarrollo humano similar, utilizando los datos de la base de datos de la ONU.

Resultados y discusión

Análisis de los datos oficiales

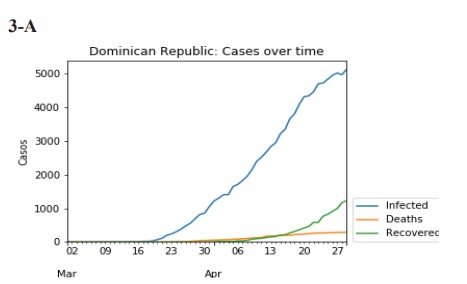
Para entender el desarrollo de esta enfermedad en el país, se analizó su expansión desde el 1 de marzo al 30 de abril del 2020 (figura 3-A). A través del gráfico se puede verificar cómo la enfermedad ha tenido un crecimiento exponencial en el país; el 30 de abril corresponde al día que se alcanzó la barrera de los 7,000 casos confirmados y 300 muertes causadas por el virus. Los datos reflejados en esta figura no incluyen los casos asintomáticos y los casos que no han sido detectados y notificados oficialmente. Según las estimaciones realizadas (Russel, Hellewell, & Abbot, 2020) al 30 de abril, en la República Dominicana solo el 16 % de los casos estaban siendo detectados y notificados oficialmente, lo que indica que el 84 % de los casos no habían sido detectados oficialmente (Ministerio de Salud Pública de República Dominicana, 2020). Según los reportes oficiales en mes de abril se habían detectado y notificado un total 7,288 casos de infecciones por COVID-19, lo que podría indicar alrededor de 38,000 casos que no habían sido detectados oficialmente. Estos números se pueden atribuir a la poca cantidad de pruebas para detectar el COVID-19 que están siendo realizadas en el país. Desde el reporte del primer caso, hasta el 30 de abril, se han hecho 28,446 pruebas, con un promedio de 900 pruebas por día, correspondiente a nueve pruebas por cada 100,000 habitantes, situación que dificulta el control de la propagación de la enfermedad.

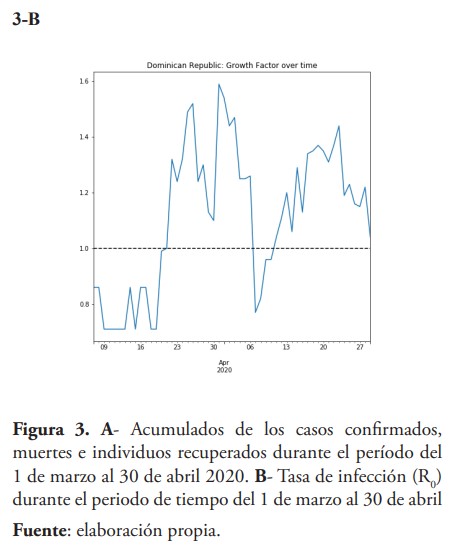
La República Dominicana muestra un factor de crecimiento de las infecciones mayor a FC>1 (figura 3-B), alcanzando la última semana del mes de abril un promedio de 1.2, lo cual indica que la epidemia presenta un crecimiento exponencial y que la enfermedad no ha alcanzado el punto de inflexión, donde tenemos un FC<1. Por lo que la cantidad de casos aumentará en las próximas semanas. Una de las posibles razones para tener este número, es que el país ha adoptado una estrategia de aislamiento social parcial, lo que permite que una cantidad significativa de personas estén expuestas al virus. La disminución pronunciada en la curva el día 7 de abril, puede deberse a un sesgo en los datos.

Modelo SIR 

El modelo SIR simple fue aplicado a los datos, y los resultados indican que el país está dentro de la fase de crecimiento exponencial de la pandemia (figura 4-A). Se puede observar que durante los primeros 20 días de la pandemia ambas tendencias se superponen, pero a partir del día 22 se puede ver cómo la tendencia cambia, presentando una cantidad de casos confirmados mayor a la cantidad de casos proyectados por el modelo. 

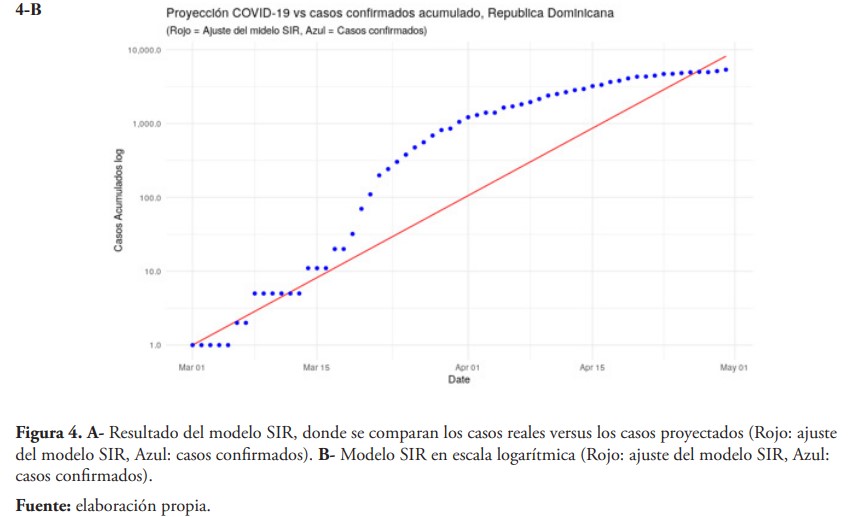
La figura (4-B), muestra el modelo en escala logarítmica, lo que permite observar las diferencias entre los datos proyectados y los casos confirmados y también se observa cómo los dos modelos difieren. El gráfico indica cómo los primeros cinco días de la pandemia los casos confirmados fueron menores a los proyectados, a partir de esta fecha tenemos una tendencia que sigue en aumento, en una tasa mayor a la exponencial. Con este modelo se obtuvo un R₀ = 1.3, lo que indica que cada persona infectada puede estar contagiando a 1.3 personas.

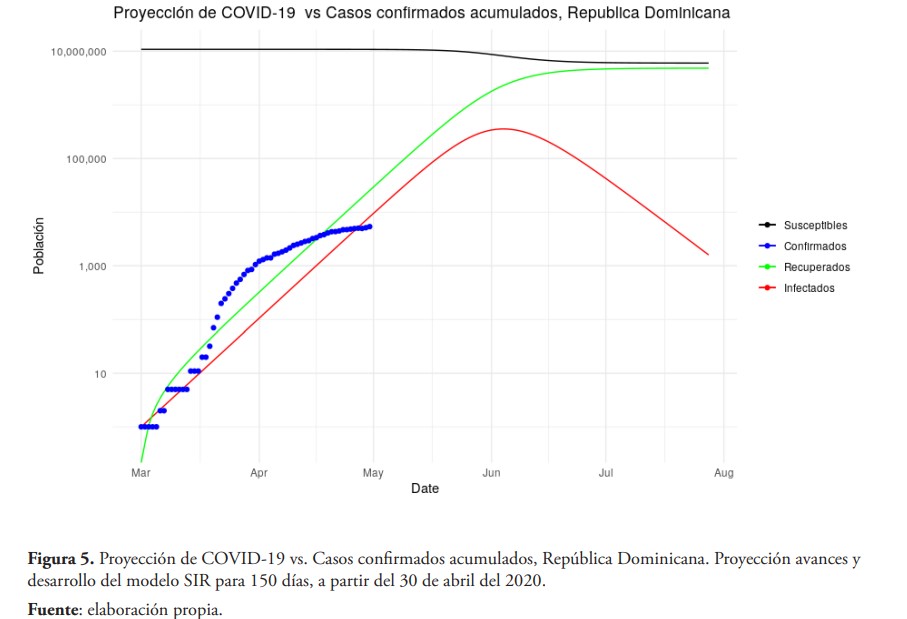
La figura 5 muestra proyecciones del modelo SIR para los próximo 150 días, en el peor de los escenarios, es decir, que no se haya tomado ninguna medida de distanciamiento social, o que las medidas adoptadas no sean efectivas para mantener el respectivo distanciamiento. Como se puede observar, el punto de inflexión del modelo está ubicado próximo al día 6 de junio, con aproximadamente 355,000 infectados por el SARS-CoV-2. Tomando en cuenta la tasa de mortalidad en promedio 4.5 % estimada por Roser, Ritchie, Ortiz-Ospina, y Hansell (2020), podemos estimar una cantidad de óbitos en 16,015 y un total de 71,179 casos graves (20 %) al final de la primera fase de la pandemia. Basados en los datos obtenido por este modelo podemos verificar la importancia de tomar medidas que permitan contener la expansión del virus, debido a que bajo este escenario el sistema de salud no tendría capacidad para brindar atención adecuada a toda la población, además de que podría impactar la economía del país.

Modelo SEIR-Extendido

Para entender mejor cómo es el proceso de propagación e incubación del virus en la población, se ha implementado el modelo SEIR extendido. Para ajustar el modelo a la realidad dominicana, el R₀ fue establecido entre 1.04 y 1.10, cálculo promedio obtenido a partir de los datos de MSP (2020) y Johns Hopkins University (2020). 

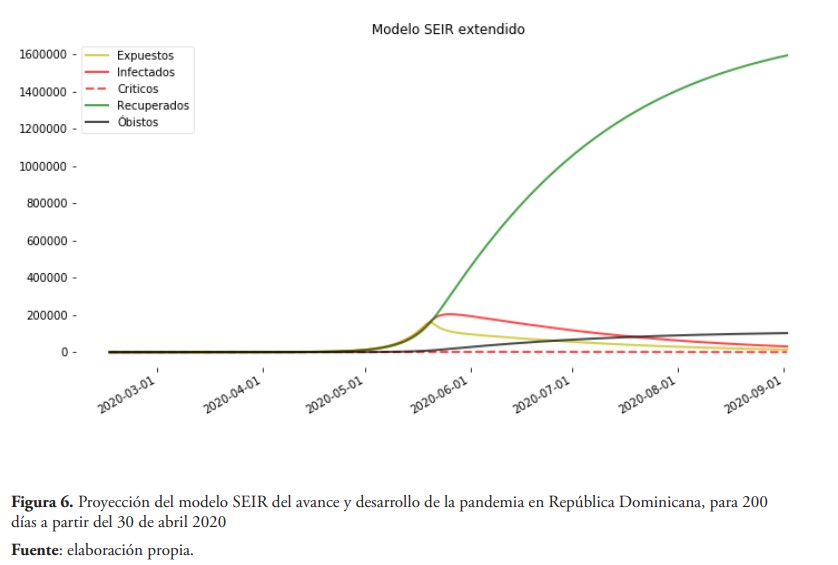
La figura 6 muestra las proyecciones del modelo para los próximos 200 días, según los datos, el pico de la curva de crecimiento del virus será alcanzado aproximadamente entre los días 31 de mayo al 4 de junio 2020, con un aproximado de 200,000 infectados por el virus, de estos el 9 % necesitaría cuidados especiales en la UCI y el 79 % de los pacientes en la UCI no superarían la enfermedad. El número total de fallecidos relacionados con el virus estaría próximo a los 1,600 casos. El modelo proyecta una tasa de fatalidad de máxima del 6 % y un R₀ máximo de 3.

Modelo log-lineal

Para entender el crecimiento epidemiológico del virus en la República Dominicana, los datos fueron modelados con el modelo log-lineal. La figura 7-A, muestra el desarrollo de la enfermedad (casos confirmados) durante los 60 días que fueron analizados en este estudio, alcanzando el pico más pronunciado el día 16 de abril, a partir de este día podemos observar una leve disminución de los casos confirmados, aunque no se puede inferir que se haya iniciado el descenso de la curva, debido a que la tasa de infección permanece entre 1.2 y 1.3, lo que indica que la epidemia todavía se mantiene en fase de crecimiento exponencial.

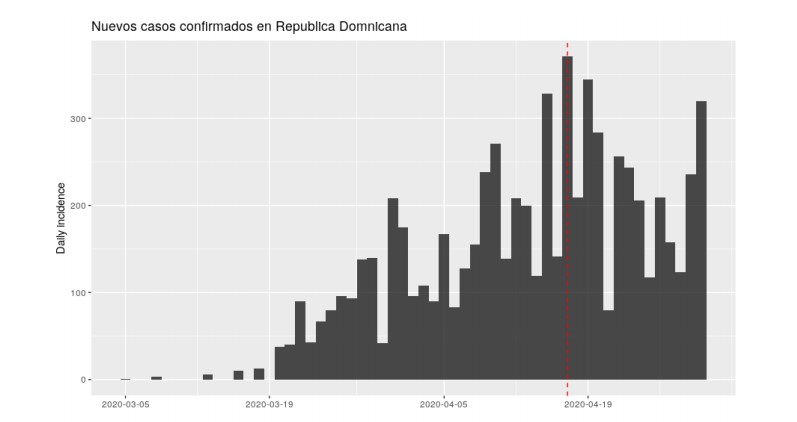
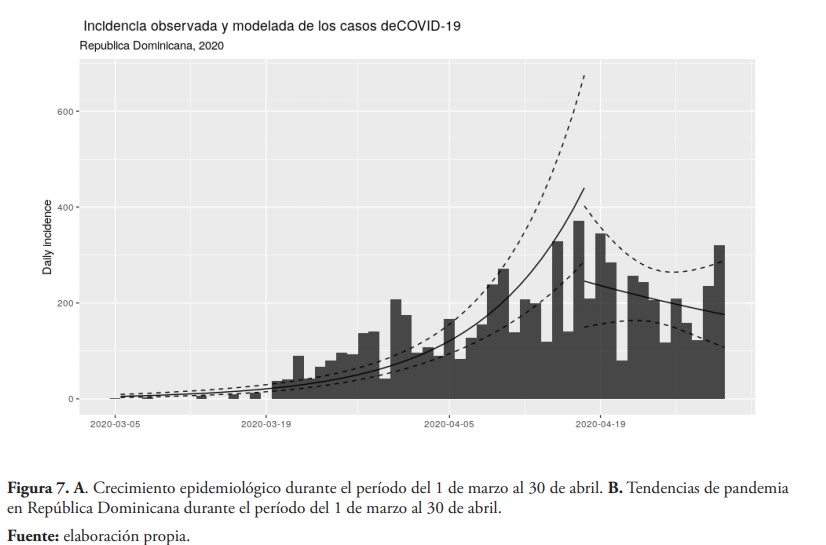
La figura 7-B muestra un ajuste del modelo antes y después del pico; ante del pico la tasa de crecimiento estaba en 0.10 y la tasa de reducción después del pico fue solo de -0.026. Esta tasa de crecimiento representa un tiempo de duplicación de los casos de 6.7 días.

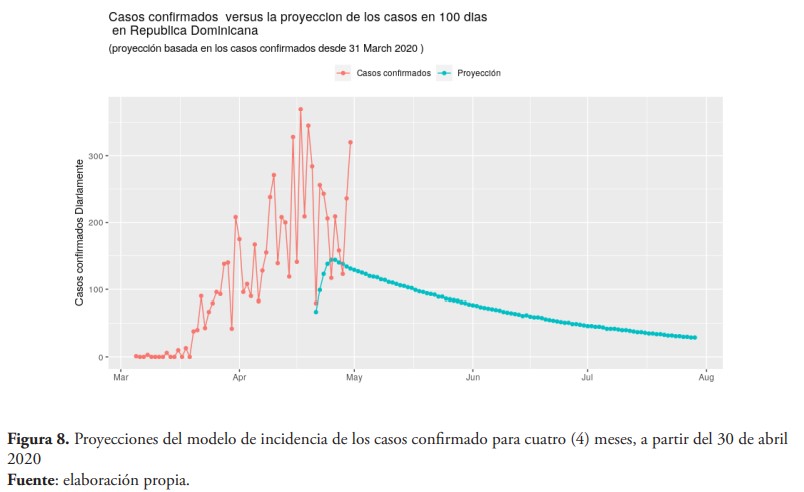
Basada en la incidencia de casos diarios reportado durante el intervalo de tiempo analizado, se hizo la proyección de los casos esperados para los próximos meses. La figura 8 muestra una proyección de casos para los próximos cuatro meses. Como se puede observar en la imagen, los caso confirmados comienzan a disminuir a partir de la segunda mitad del mes de mayo, llegando a menos de 50 casos por día, a partir del inicio del mes de julio.

Conclusiones

La pandemia del COVID-19 se ha extendido por la mayoría de los países del mundo, obligando a que los gobiernos tomen medidas sin precedentes, para mitigar la propagación del virus. De este modo se ha generado una gran presión en los sistemas de salud de estos países, los cuales no estaban preparados para una crisis de esta magnitud; ha quedado evidenciado que los recursos y la infraestructura sanitarias son insuficiente para manejar el gran volumen de casos.

En este trabajo fueron implementados los modelos SIR, SEIR y log-lineal, para modelar los posibles escenarios y evaluar el impacto de la pandemia en República Dominicana, además del efecto de las medidas tomadas por las autoridades. Los modelos son esenciales para entender el desarrollo y la evolución de las enfermedades y epidemias proyectando los posibles escenarios que pueden suceder, lo que permite que diversas decisiones puedan ser tomadas por las autoridades competentes con el fin de contener la propagación del patógeno. Las estimaciones obtenidas por los modelos no difieren mucho de otras estimaciones ya realizadas para el país (Luo, 2020), que estiman la disminución de los casos entre mayo y junio. Los resultados obtenidos en este estudio pueden ser utilizados para la toma de decisiones que permitan una reactivación de la sociedad de forma gradual, y de este modo disminuir los riesgos de una nueva ola de contagios.

Las aproximaciones presentadas a partir de los datos y modelos obtenidos no necesariamente predicen por completo el comportamiento de la pandemia, debido que esto pueden ser afectados por diversos factores y variables (sociales, económicas y culturales) que no pueden ser introducidos dentro del modelo, además la variación de los datos es constante, lo que puede cambiar de forma drástica las tendencias y proyecciones. Otro factor importante para la construcción de los modelos es la calidad y la disponibilidad de los datos. En la República Dominicana hay dificultad para acceder a los datos, además, existen variables que no son recolectadas y medidas por los órganos gubernamentales, lo que implicó una de las mayores limitaciones de este estudio. Por esta razón, no fue posible proyectar modelos robustos que pudieran medir el impacto del aislamiento social en las diferentes regiones y ciudades del país. 

Se debe resaltar que los resultados deben interpretarse con cuidado, ya que las proyecciones en estas etapas de desarrollo y crecimiento de la curva epidemiológica dependen mucho de la calidad de los datos, pequeños cambios en los valores observados pueden producir grandes variaciones de tendencia en las proyecciones.

Disponibilidad de los datos y códigos

Los datos y códigos usados en este estudio están disponibles en https://github.com/edianfranklin

Agradecimientos

El presente trabajo fue desarrollado con el apoyo del Ministerio de Educación Superior Ciencia y Tecnología de la República Dominicana a través del proyecto: Mapeo de resistomas en los ríos Yaque del Norte y Yaque del Sur y sus implicaciones para la salud humana. 

Asimismo, contó con el apoyo de la Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES) – Código de Financiamiento 001.